基于交通卡数据的地铁疫情传播模型

王欣宇，孟品超

（长春理工大学 数学与统计学院，长春 130022）

COVID-19新冠肺炎在全球范围内的持续爆发严重影响着人们的健康。研究结果表明，乘客在乘坐公共交通工具时，密闭拥挤的环境为新冠病毒的传播提供了有利条件，并且疫情也极易沿着交通线路进行大范围的扩散［1］。与黑死病、天花、SARS疫情爆发时期相比，如今更加发达的公共交通系统已经成为居民出行的首要选择［2］，加大了疫情通过公共交通系统传播的可能。

由于人类尚未完全掌握COVID-19新冠肺炎的流行病学特征，所以新冠肺炎的传播研究主要依据SARS和流感等呼吸性传染病的研究。张殿业［3］基于模糊决策建立交通运输系统突发疫情的扩散模型，判断不同交通运输方式的疫情扩散概率。Gerardo C［4］基于SEIR模型计算SARS在不同防疫措施下的感染人数后发现：口罩、消毒、降低人口密度都是减缓疫情传播的重要手段，隔离与病患接触的人群是最有效的防控手段。Salathe M［5］基于网络结构，模拟 H1N1 流感病毒在学校内部因社交接触的传播过程，判断个体感染的概率，并且计算人群中不同的疫苗接种率对感染人数的影响。

考虑到新冠肺炎存在潜伏期［1］，对新冠肺炎的传播动力学研究多基于 SEIR 模型［2，6，7］。张宇［2］针对交通工具内部空间狭小、乘客之间接触率高等特点对SEIR模型进行改进，建立交通工具内部新冠肺炎疫情的传播模型。Joseph T.Wu［6］基于人口流动性对SEIR模型进行改进，对人口流动性大的城市进行新冠肺炎病例数量预测。Zhou Y［7］在研究城市人口移动对新冠肺炎的传播造成的影响时，基于深圳市的手机信令数据和SEIR模型，模拟不同的人口移动程度下疫情的传播情况。

总体而言，目前对呼吸性传染病在交通领域的传播研究缺乏足够的理论支撑，并且在疫情发生时尚未充分利用居民的出行数据对病毒接触者进行科学有效的监管。地铁是城市最主要的公共交通工具之一，地铁交通卡数据记录了乘客的出行信息，可以在疫情传播时对乘客进行轨迹追踪，同时记录了乘坐地铁人数的动态变化，为传染病在公共交通工具中的传播提供可信度较高的预测。本文建立地铁疫情传播模型，根据杭州市真实的轨道交通客流数据模拟疫情在地铁中的传播情况，分析通风、消毒、佩戴口罩和接种疫苗等防疫措施引起的参数变化对疫情传播规模的影响，给出合理的轨道交通系统的疫情防控方案。

1 疫情在直达交通工具中的传播

乘客在乘坐地铁时，密闭的车厢环境和不断上下车的人流都会影响疫情的传播，为了建立轨道交通系统疫情传播模型，首先需要探究无乘客中途上下车的直达交通工具中的疫情传播情况，建立直达交通工具的疫情传播模型，并找出影响交通工具中感染概率的因素，为地铁疫情传播模型的建立提供参考。

1.1 直达交通工具中的疫情传播模型

由于新冠肺炎在人体内存在潜伏期，因此新冠肺炎的疫情传播模型常采用SEIR模型［10］，SEIR传染病模型将总人口分为：易感者（S）、潜伏期感染者（E）、患病者（I）和康复者（R），其中：S是指未被感染但是对病毒没有免疫能力的人群；E是指已被病毒感染但尚未具有传染能力的人群；I是指已经患病并具备传染能力的人群；R是指治愈后或未染病但具备免疫能力的人群。设N为人口总数，在不考虑人口出生、迁徙、死亡等外界环境干扰的状况下，四类人群在时间t内数量变化率可表示为：

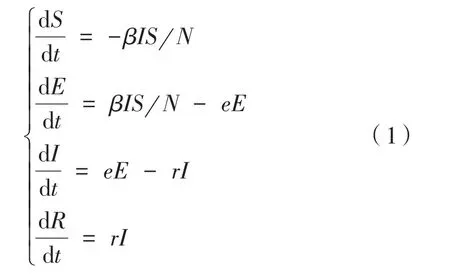
式中，β表示病毒的感染率，指时间t内易感者与患病个体接触并感染的概率；e表示潜伏期感染者转化为患病者的概率；r表示患病者康复的概率；S/N表示人群中易感个体的比例。由于在疫情传播早期人群对新型冠状病毒普遍易感［1］，因此N=S0+I0。

式（1）的SEIR模型可作为中途无乘客上下车的直达交通工具疫情传播模型，由于交通工具环境封闭，在患病者与其他乘客密切接触的过程中，感染率β与患病者的乘车时间、交通工具内部病毒的密度等影响因素密切相关，因此，为了计算乘车时间内密闭交通工具中新被感染的人数，还需找出影响交通工具内部的感染概率β的因素。

1.2 密闭交通工具中感染概率的计算

当患病者与易感者同时乘坐密闭交通工具时，感染率β(t)满足如下关系式［9］：

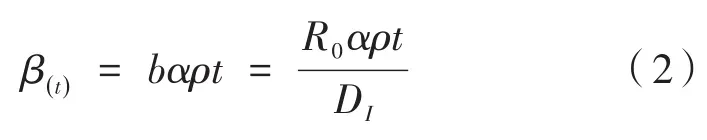
式中，b表示易感者与患病个体接触后感染的概率，它与新冠肺炎传播时的基本再生数R0（每位患病者平均传染的人数）和感染间隔DI（易感者感染病毒后再传染其他易感者的平均时间）有关［6］；α表示易感者与患病者的接触概率，当交通工具内部空间无间隔时，α=1；t表示乘坐时间，计量单位为小时；ρ表示密闭交通工具中的病毒密度。

病毒密度ρ满足如下关系：

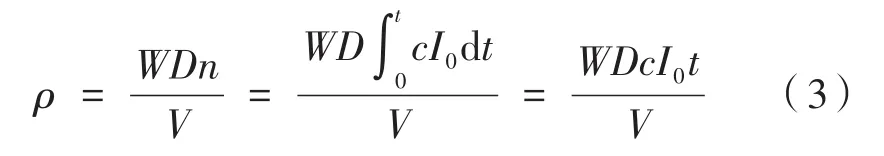
式中，n表示病毒数目，它可进一步用初始患病者的人数I0和乘车时间t表示；V为交通工具的体积；W为通风指标，病毒匀速向外排出后交通工具内部剩余的比例；D为消毒指标，病毒被匀速杀死后交通工具内部剩余的比例；c为病毒释放强度，与患病者的发病状况有关。c、W、D为定量化的评估指标，其中W和D的最大取值为1，此时交通工具内部未采取任何的通风和消毒措施，数值越小说明通风和消毒的效果越好［9］。

将式（2）和式（3）联立，可得感染率β(t)的完整表达式：

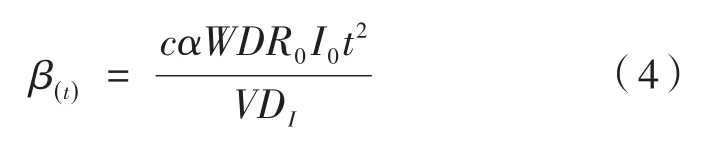
由式（4）可以看出，交通工具的感染率β(t)与车厢内部的通风强度W、消毒强度D、初始时刻交通工具内含有的患病者人数I0及其病毒释放强度c、乘车时间t、交通工具的体积V、与病患的接触概率α，病毒的基本再生数R0和感染间隔DI有关。如果在乘客乘车过程中采取一些防疫措施，例如要求乘客佩戴口罩或者保持交通工具中的通风、消毒，会引起式（4）中部分参数的改变，从而影响乘客在乘坐交通工具时被感染的概率。

1.3 直达交通工具中感染人数的计算

在交通工具的感染率β(t)已知的情况下，如果在患病者乘车过程中没有乘客中途下车，可以利用式（1）计算在患病者乘车时间t内交通工具中的被感染的人数。由于乘客乘坐交通工具的时间远小于病毒的潜伏时间和感染间隔［13］，所以直达交通工具中新被感染的人数ΔE(t)就是易感者减少的人数，且新被感染的人群在乘车过程中不会转为具有传染能力的患病者。

将式（1）和式（4）联立：

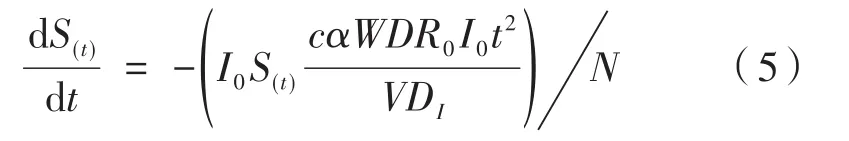
整理后移项有：

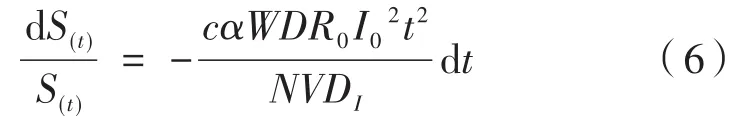
等式两边积分得：

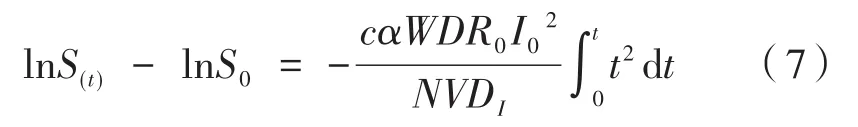
整理得到：

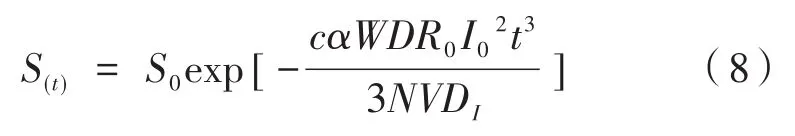
因此，交通工具中新被感染的人数ΔE(t)可表示为：

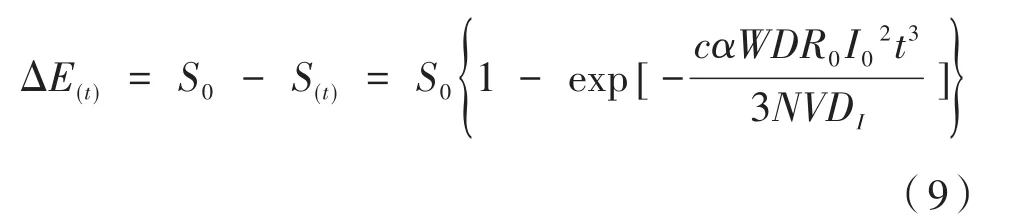
式（9）可以计算直达交通工具中新被患病者感染的人数，适用于飞机、火车等长时间行驶的交通工具，然而在轨道交通系统中，地铁行驶时间短并且频繁停靠站点，在患病者乘车过程中存在大量的人口流动，因此，地铁疫情传播模型还需要考虑人口流动对地铁中疫情传播的影响。

2 疫情在地铁中的传播

尽管乘客进入轨道交通系统后，除乘坐地铁外，还可能会停留在地铁站内部进行候车、换乘等活动，但是由于乘客在站内停留时间相对较短，且乘客因不断移动而几乎不会造成与其他乘客的密切接触，因此在研究轨道交通系统疫情传播时，本文只考虑地铁车厢内部的疫情传播情况。疫情在地铁中进行传播时，由于地铁在行驶过程中人口流动性较大，车厢中动态变化的人口数影响着地铁中易感者和新被感染的潜伏期感染者的数量变化，所以为了计算地铁疫情传播规模，需要结合人口流动对SEIR模型进行改进，建立地铁疫情传播模型，继而计算地铁中被患病者感染的人数。

2.1 地铁疫情传播模型

人口流动影响着地铁中疫情传播情况［6］，假设中途进入地铁的人群均为未被病毒感染的易感者，LI(t)表示时间t内进入某辆地铁的人数，LO(t)表示同时间段内从该辆地铁离开的人数，N表示时间t内乘坐过地铁的人口总数，则易感者人数S(t)的变化率除了时间t内地铁中新被感染的人数外，还要增加该段时间上车的人数LI(t)，减去下车的人群中未被病毒感染的人数(LO(t)/N)S(t)，则S(t)的变化率可表示为：

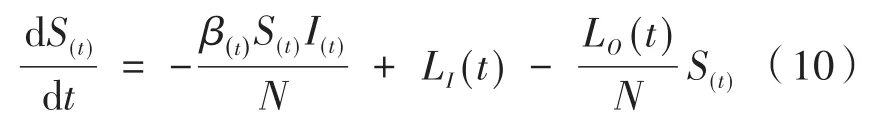
同理，潜伏期感染者人数E(t)和患病者人数I(t)的变化率也需要减去下车人群中新被病毒感染的人数(LO(t)/N)E(t)和患病者人数(LO(t)/N)I(t)。由于地铁是密闭的交通工具，感染概率β(t)由式（4）计算得到。因此，地铁疫情传播模型可表示为：

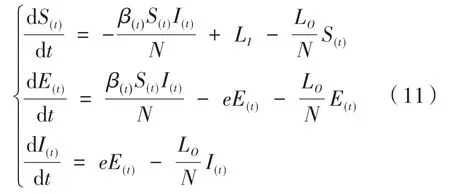
由于乘客乘坐地铁的时间远小于病毒在人体的潜伏时间［13］，所以若初始时刻进入地铁的只有易感者和具有感染能力的患病者时，地铁中新被感染的人数就是时间t内潜伏期感染者增加的人数ΔE(t)，假设新感染的人群在乘车期间不具备二次感染能力，则时间t内地铁中新被感染的人数变化满足如下关系：

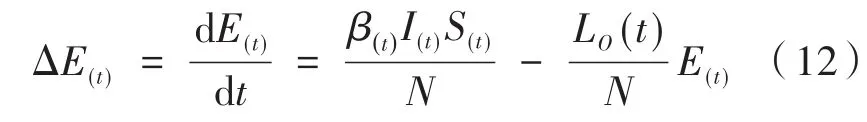
地铁疫情传播模型综合考虑地铁的空间密闭性和人口流动性对疫情传播的影响，以微分方程的形式反映易感者、潜伏期感染者和患病者三类人群数量的变化，为了更加直观地判断轨道交通系统中疫情的传播规模，还需计算地铁中新被患病者感染的人数。

2.2 轨道交通系统中感染人数的计算

计算地铁中新被感染的人数可以直观地反映出轨道交通系统中的疫情传播规模，便于对比不同防疫措施对疫情传播的影响。由于地铁行驶的站点数量可以反映乘车时间，为便于计算，设ti为地铁到达第i个站点的时间，βi、Ii、Si表示ti时刻地铁中的感染率、患病者人数、易感者人数，求解式（12）的一阶非齐次线性微分方程，可得到ti时刻地铁到达第i个地铁站时车厢内被患病者感染的人数Ei，满足如下关系式：

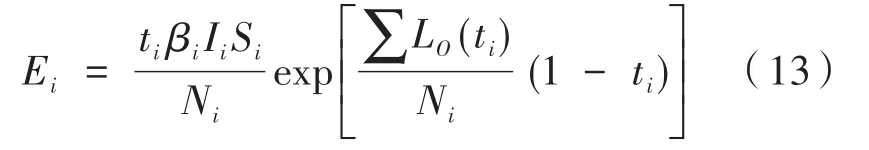
式中，Ni、∑Lo(ti)分别表示患病者乘车的ti时间段内乘坐过该辆地铁的总人数和该时间段下车的总人数。由于地铁的行驶时间远小于被病毒感染的乘客转成具有感染能力的患病者的时间［13］，地铁内患病者人数始终为I0，此外，在乘坐地铁中被感染的乘客还有中途下车的新被感染的乘客，因此，乘客在时间ti内乘坐地铁时新感染的人数ΔE(ti)可表示为：

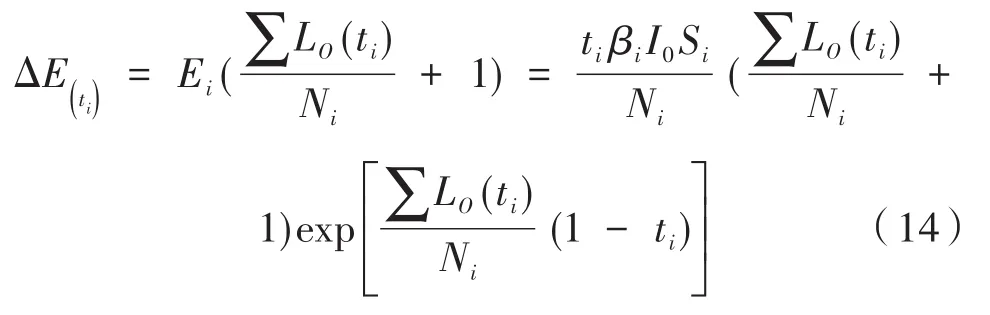
式（14）可以计算地铁中新被患病者感染的人数，它与ti时刻地铁内部的感染率βi、患病者人数I0、易感者人数Si（可用ti时刻地铁内部的人数减去患病者人数近似计算）、时间ti内乘坐过该辆地铁的总人数Ni及每个地铁站下车的人数LO(ti)密切相关。

3 数值实验

在进行地铁疫情传播模型的数值实验时，为了使实验结果更具有参考价值，本文使用杭州市真实的地铁交通卡数据进行乘客的轨迹提取和上下车人数的测算。对比地铁与其他交通工具的疫情传播规模可以判断人口流动性对疫情传播的影响。此外，还需要找出不同防疫措施对疫情传播的影响，从而找到合理的轨道交通系统疫情防控方案。

3.1 数据预处理及主要参数说明

本文使用2019年1月杭州市地铁交通卡数据进行地铁上下车人数的测算，地铁线路简图如图1所示。地铁交通卡数据详细地记录了每位乘客使用的交通卡ID号码，进出地铁站的编号、所在线路及进出站时间等信息，对原始数据进行清洗和整理后，计算乘客每次乘车的时长和乘坐路线。

图1 2019年1月杭州市地铁线路简图

对乘客乘坐地的时间进行分段统计，杭州市地铁2019年1月日均客流量如图2所示，客流高峰时间主要集中在 8：00—9：30和 17：30—19：00两个时间段。

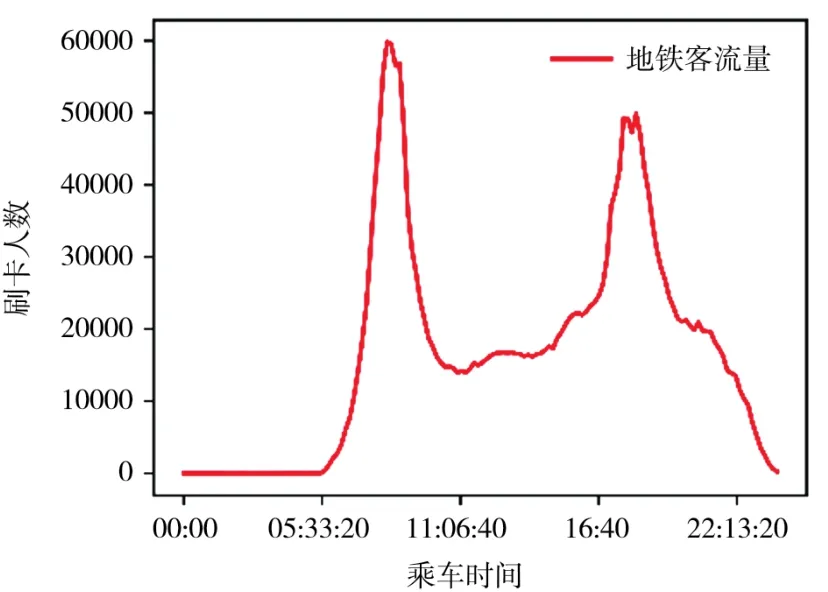
图2 杭州市2019年1月日均客流量统计图

在进行数值实验时，首先随机抽取一名乘客假设为新冠肺炎的患病者，根据患病者的某次乘车信息模拟疫情在地铁中的传播情况。其次，统计地铁车厢内动态变化的人数计算地铁疫情传播规模，由于同一辆地铁的乘客在同一站点下车时会产生聚集现象，因此可以根据每个地铁站的进出站记录和地铁的行驶时间提取出乘坐过同一班地铁的乘客乘车信息，在进行流行病学调查时，一旦发现新冠肺炎确诊者，对与患病者乘坐过同一辆地铁的乘客进行有效的隔离和身体状况监测，可以减缓疫情的进一步传播。经统计，患病者在某次出行中沿途各站信息和上下车人数记录如表1所示，t0时刻地铁内部的初始乘客数量N0为105，患病者乘车时间t内人口流动量N(t)为659。

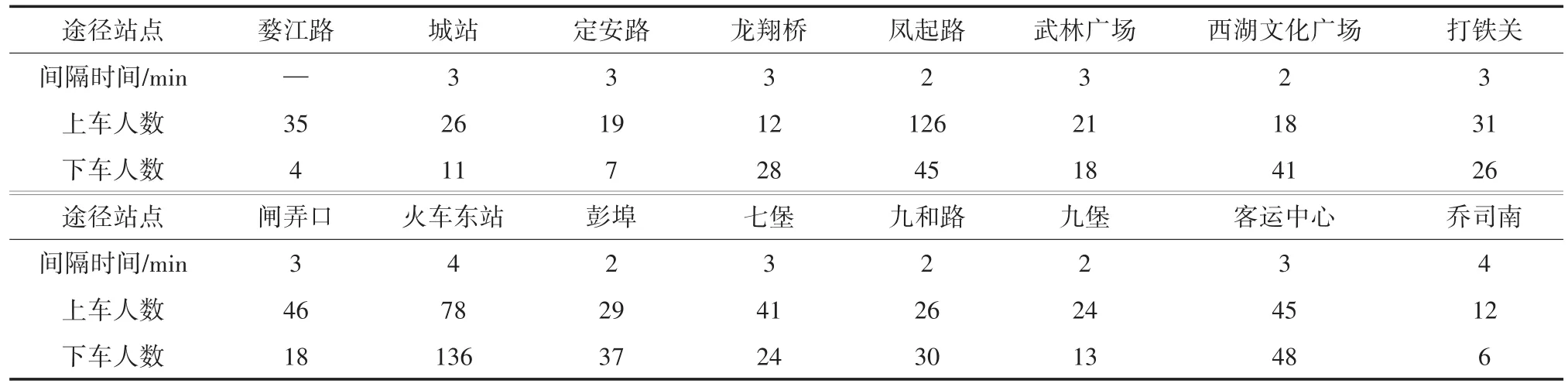
表1 患病者在乘车过程中的途径站点与上下车人数变化

此外，还需要设置合理的参数模拟新冠肺炎在地铁中的传播。杭州市地铁型号为6节B组车厢，车厢内部互通，每节车厢的长、宽、高分别为：20 m、2.8 m、2.2 m。现有研究成果表明，新冠肺炎的基本再生数R0的估计范围为2.6～3.0［7］，传染间隔DI的估计值是 7.5 天［13］，因此，本次数值实验中设R0=2.7，DI=7.5d。参考“非典”时期的病毒释放强度［9］，假设患病者的病毒释放强度c=10。

轨道交通系统疫情防控措施主要有：减少地铁乘坐人数、通风、消毒、乘客佩戴口罩和疫苗接种，不同的防疫措施会引起相关参数的改变，其中：减少地铁乘坐人数会引起参数Ni和LO(i)的改变；通风、消毒和乘客佩戴口罩会引起感染率βi中通风指标W、消毒指标D和病毒释放强度c的改变，但地铁只能到达终点站后才能进行消毒工作；疫苗接种会引起易感者人数Si的改变。研究表明，乘客在佩戴口罩后病毒的传播强度减弱64%［19］。计算地铁在不同防疫措施下的感染人数可以判断轨道交通系统中防疫措施的有效性，并给出合理的轨道交通系统疫情防控方案。

3.2 人口流动性对疫情传播的影响

为了探究人口流动性对疫情传播的影响，首先对地铁与直达交通工具的疫情传播规模进行对比。假设在患病者乘车过程中，某直达交通工具的乘客人数与地铁初始乘客数量N0和直达交通工具内部的体积与地铁相同，则在相同的乘车时间内，未采取任何防疫措施的地铁与直达交通工具的感染人数对比图如图3所示，受到地铁人口流动性的影响，疫情在直达交通工具中的传播规模小于地铁的传播规模。

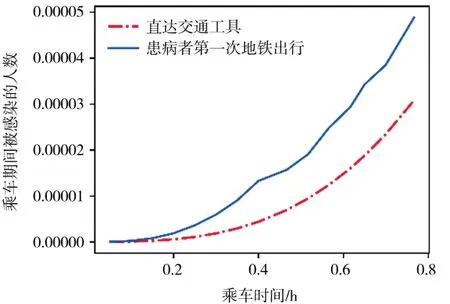
图3 直达交通工具与地铁的疫情规模对比图

为进一步探究地铁疫情与人口流动性的关系，选取患病者在不同时间段起讫站相同的四次地铁出行来进行地铁感染人数的测算，出行信息如表2所示，地铁在相同的行驶时间内患病者四次出行中的人流量分别为：550、430、659、817，测算结果表明地铁在不同时间段的人流量有显著差异。

表2 患病者出行信息

假设患病者乘坐地铁期间地铁未采取任何防疫措施，对患病者四次出行的感染人数随患病者乘车时间的变化如图4所示，结合患病者四次地铁出行的人流量数据可以看出，人口流动性越大，地铁内部的疫情传播规模越大，所以在疫情发生时，乘客需要尽量避开客流高峰时间段乘坐地铁，降低被感染的可能性。

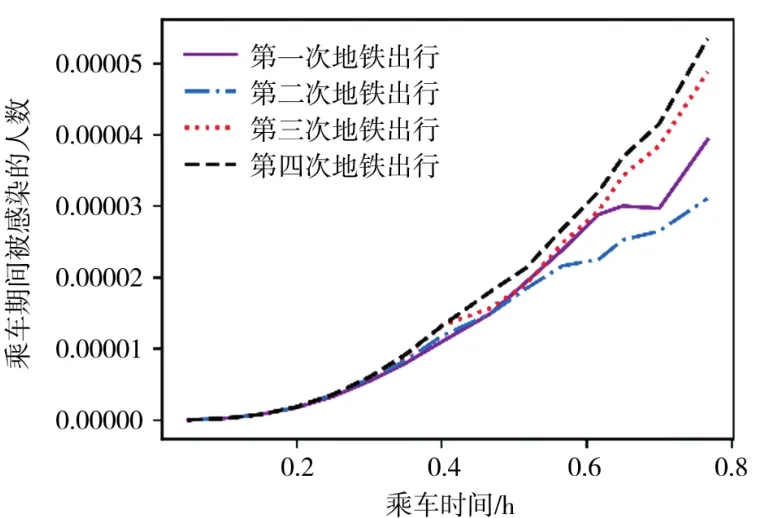
图4 疫情在不同时间段地铁中的传播规模

3.3 不同防疫措施对疫情传播的影响

在疫情发生时，除了尽量减少地铁出行的人次外，轨道交通系统的疫情防控措施主要有：通风、消毒、乘客佩戴口罩和疫苗接种。假设乘客进入地铁后全部佩戴口罩且地铁通风时病毒被匀速释放到车厢外，患病者乘车期间地铁在不同的通风强度下参数和乘客被感染的概率等数值模拟结果如表3所示，患病者乘坐地铁期间和下车后车厢内部乘客被感染的概率如图5所示，由表3的计算结果和图5可以看出，地铁车厢内部的通风强度越大，车厢内乘客被感染的概率越低，并且当地铁的通风强度大于等于3倍密封状态下的空气流通速度时，地铁行驶到终点前乘客被感染的概率已经降为0，无需在终点处采取消毒措施。

表3 不同通风强度下乘客被患病者传染概率的数值模拟结果

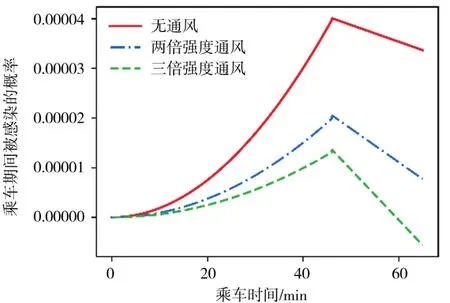
图5 不同通风强度下乘客被感染概率对比图

疫苗接种率对轨道交通系统疫情传播规模的影响如图6所示，当人群的疫苗接种率达到70%时，疫情在地铁中的传播规模与乘客佩戴口罩的传播规模相当，此时，结合地铁的通风消毒措施，轨道交通系统的疫情可以得到良好的控制，乘客在进入地铁后可以不用强制佩戴口罩。

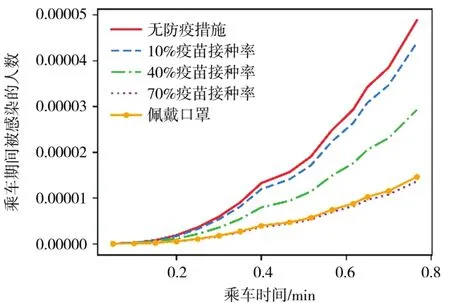
图6 疫情在不同疫苗接种率下传播规模的对比图

3.4 地铁疫情防控方案

通过数值实验结果可以看出，当出现新冠肺炎疫情时，乘客需要尽量降低地铁出行的频率并避开客流高峰搭乘地铁，在乘客进入地铁后除了佩戴口罩外，地铁车厢还需要保持空气流通，降低乘客被病毒感染的概率，通风强度至少大于地铁在密封状态下3倍流通速度，并注意地铁车厢内部不定期的消毒。在接种疫苗时，当人群中疫苗接种的覆盖率达到70%以上时，乘客进入地铁无需被强制要求佩戴口罩。

4 结论

本文基于交通卡数据建立地铁疫情传播模型，在疫情爆发时可以根据乘客出行信息判断患病者乘坐地铁时的传染规模，也可以对乘客进行轨迹追踪，对有被传染可能的乘客进行有效隔离防止疫情的进一步扩散。在探究不同的防疫措施对疫情传播带来的影响时发现，佩戴口罩并保持地铁中的通风消毒是轨道交通系统中最有效的防疫措施，当人群中的疫苗接种率达到70%以上，轨道交通系统中的疫情传播将会得到有效的控制。

本文仅考虑患病者一次乘车过程中对疫情传播的影响，但是在实际中，患病者以及在地铁中被感染的乘客可能在未有明显新冠肺炎症状时多次乘坐地铁，造成疫情在轨道交通系统的多次传播，因此，未来的研究方向将注重患病者的多次乘坐地铁对疫情传播带来的影响。

受到数据的限制，本文仅对新冠肺炎疫情在地铁中的传播进行了讨论，并利用2019年1月的杭州市地铁刷卡数据进行模拟，但是交通卡数据使用疫情发生之初的交通卡数据具有更好的研究意义，建立的疫情传播模型可以适用于公共汽车、高铁等交通工具，提出的疫情防控措施也适用于其他公共交通系统的呼吸性传染病疫情防控。