基于故障模式及失效机理分析的电液伺服阀寿命分析*

王洪波,黄智鹏,柳志姣,高 宾,徐悦鹏,俞 滨

(1.航空工业庆安集团有限公司,陕西 西安 710077;2.燕山大学 机械工程学院,河北 秦皇岛 066004)

0 引 言

电液伺服阀是电液伺服控制系统的关键元件,因其具有动态响应快、控制精度高、使用寿命长等优点,被广泛应用于航空、航天、船舶等各个领域[1]。

高可靠、长寿命是机载产品的发展趋势和重要指标,电液伺服阀的寿命要求通常在百万次上下。如果仅通过试验结论确认寿命指标是否满足要求,存在周期长、成本高等问题,且无法满足购买方的交付要求[2]。

寿命作为一项技术指标是由设计来保证的,而不是由试验来保证的,因此,对电液伺服阀寿命进行预测与分析显得尤为重要。

崔振兴[3]进行了工程应用试验,利用典型产品的工程应用试验数据,参照《航空机载设备技术寿命和可靠性评估的一般程序和方法》,对伺服阀的技术寿命进行了评估,初步确定了该阀的技术寿命平均值,同时对电液伺服阀在工业应用中的失效准则和失效模式做了分析。宗满意等人[4]发明了一种双路电液伺服阀寿命试验及测试装置,可以同时进行寿命试验与性能测试,利用控制用伺服阀可实现两台试验产品状态的自动切换。ZHANG Kun等人[5]基于冲蚀磨损的失效机制,提出了一种电液伺服阀的退化评估与寿命预测方法,采用该方法预测结果表明,双喷嘴挡板阀和滑阀的结构磨损与性能特性的退化有关;并采用计算流体力学和冲蚀理论相结合的方法,建立了湍流磨损和冲蚀磨损的数学模型。高婷[6]提出了一种电液伺服振动台寿命的模糊数学评估模型,以电液伺服振动台的安全性、可靠性、经济性、技术性评价指标等为基础,构建了电液伺服振动台寿命评价指标体系;在此基础上,建立了模糊数学评价模型和评价因子集,采用改进的层次分析法确定了评价因子的权重集,采用指数法定量计算了单因素评价指标,建立了模糊关系的定量评价矩阵,得到了各层次的综合评价结果,有效地评价了电液伺服振动台的使用寿命。康凯旋[7]研究了MOOG-G761双喷嘴挡板电液伺服阀故障预测的问题,针对常见的电液伺服阀故障,建立了故障预测目标与评价指标,探索了电液伺服阀故障预测策略。

上述研究取得的研究成果可为电液伺服阀故障预测的推广奠定理论基础:(1)以伺服阀结构组成、工作机理以及动静态特性为基础,建立了电液伺服阀数学模型,分析了液压油温度、污染颗粒特征,归纳了伺服阀故障分类,揭示了伺服阀故障发生机理;(2)基于伺服阀故障机理,针对不同故障类型的电液伺服阀的结构参数对流量、压力、内泄漏的影响进行了灵敏度分析,得到了不同故障发生的原因以及其对伺服阀性能的影响程度;并重点分析了阻尼孔堵塞和滑阀阀芯磨损对伺服阀性能的影响规律。

李瑜等人[8]提出了一种机载模型监控方法,采用AMESim工具进行了系统的建模,对模型进行了校准、实时化和线性化处理;在对监控算法进行了设计与仿真之后,用C代码编程实现了模型监控算法,并将其运行于发动机电子控制器;对某发动机燃油计量装置的试验结果表明:机载模型监控可以有效监测系统中因元部件性能衰减、卡滞、零偏漂移等引起的异常或故障,并能补偿电液伺服阀的零偏漂移和容错运行,避免了控制功能失效或过快降级。该结果可为航空发动机及相关领域的电液伺服系统机载模型监控设计提供参考。

笔者通过调查发现,目前对电液伺服阀故障模式及失效机理进行的分析较少,且对建立完整的电液伺服阀寿命评估方法的研究不足。在相关研究中,并没有依据电液伺服阀现有的可靠性数据,对威布尔模型的形状参数进行合理选取,且对关键部件进行寿命预测模型分析。

FMMEA作为故障模式和机理分析方法,通常通过统计、试验、分析、预测等方法获得产品的故障模式,从国内外标准、手册中获取失效率数据,该方法已经广泛应用于产品可靠性分析中。因此,针对寿命设计需求及寿命试验,基于FMMEA的寿命预测对寿命工作开展有重要的指导意义。

综上所述,为了提高各种因素下电液伺服寿命分析的准确性,笔者提出一种基于故障模式及失效机理分析(FMMEA)的电液伺服阀寿命分析方法。

首先,以电液伺服阀为研究对象,通过对电液伺服阀进行故障模式及失效机理分析(FMMEA),确定电液伺服阀耗损机理和寿命特征;然后,依据现有的故障数据及应力类型,建立电液伺服阀寿命预测模型,并对其进行寿命评估;最后,建立电液伺服阀可靠性模型,并进行电液伺服阀的寿命分析,为电液伺服阀产品寿命设计提供依据。

1 电液伺服阀介绍

作为电液伺服或比例控制系统的核心元件,电液伺服阀在工程技术领域中得到了越来越广泛的应用[9]。它的可靠性对整个伺服控制系统的可靠性和安全性至关重要[10]。

依据液压放大级的不同,电液伺服阀可分为3种,即喷嘴挡板式电液伺服阀、射流管式电液伺服阀和射流偏转板式电液伺服阀。其中,射流偏转板式电液伺服阀由力矩马达、射流式液压放大器、滑阀组件和反馈组件组成。

射流偏转板式电液伺服阀的结构原理图如图1所示。

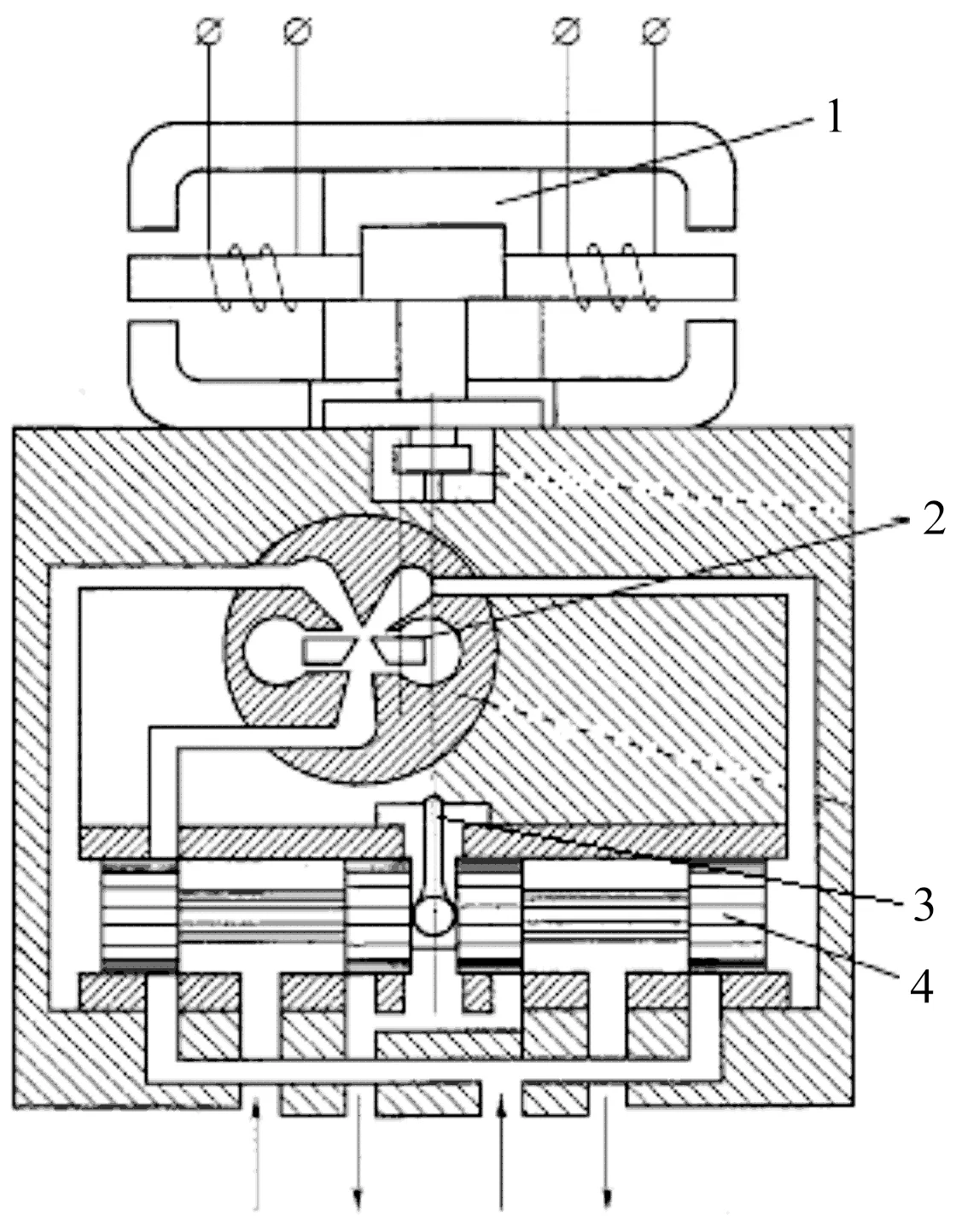
图1 射流偏转板式电液伺服阀结构原理图

电液伺服阀接受控制器的电信号时,会输出相应极性、成比例的控制负载流量,在系统中起着电液转换和功率放大的作用。

2 电液伺服阀的FMMEA分析

失效模式和影响分析是计划质量工具的一种方法,用于识别可能影响过程的故障,并对系统、产品或服务的风险进行优先排序。

结合电液伺服阀的使用环境、工况及其结构特点,以及同类产品或相似产品的已有故障信息及数据,笔者需要对电液伺服阀进行故障机理和影响分析,并确定其产品的损耗故障模式(即疲劳、老化、磨损等),以及影响电液伺服阀使用安全和寿命的主要故障模式。

在可靠性试验中,针对可靠性指标验证和评估的问题,在现有以寿命为特征量的可靠性试验方法上,笔者对其进行了发展和完善,提出了一套完整的可靠性寿命试验与评估方法[11],即基于故障模式及失效机理分析(FMMEA)的电液伺服阀寿命分析方法,用于控制和防止过程错误[12]。

依据电液伺服阀的组成,笔者总结了其故障模式及失效机理分析(FMMEA)表,如表1所示。

表1 电液伺服阀故障模式及失效机理分析(FMMEA)

其中,电液伺服阀中的力矩马达、液压放大器、滑阀组件、反馈组件等关键部件的失效率,是根据国内外各种试验或外场收集数据的可靠性数据,按照一定的标准求得的。

2.1 力矩马达失效分析

力矩马达是电液伺服阀的重要组成部分之一,是电液伺服阀的输入级,它在电液伺服阀中起到前置放大的作用,将输入的电流信号转换为机械的转角。动铁式力矩马达主要由线圈组件、衔铁组件、永磁铁、弹簧管等组成。线圈组件产生的电磁力产生了旋转力矩,弹簧管和反馈杆的弹力产生了阻力矩。当输入某一电流,线圈产生的旋转力矩与弹簧管等的阻力矩相平衡,停到某一转角θ。

线圈受到振动、冲击等机械环境的影响,易发生焊点脱落故障;受到温度、湿热等气候环境影响,易发生漆包线腐蚀、绝缘性能降低等故障,造成线圈断路或短路,使产品完全丧失功能。弹簧反复运动,易发生弯曲、断裂,影响电液伺服阀的性能及使用寿命。

设力矩马达衔铁臂长为a(m)，中位时气隙厚度为g(m)，单个线圈匝数为NC，永久磁铁的磁势为MO(A)，衔铁处于中位时每个气隙的磁阻为Rg(1/H)，Rg=g/(μ0Ag)，空气中导磁率μ0=4π×10-7(H/m)，Aε为气隙面积。当衔铁处于中位时，永磁铁产生的磁通量为Φε，Φε=M0/(2Rε)。

笔者以衔铁组件为对象，列出衔铁组件的动力学方程为：

(1)

式中：Ki—力矩马达的力矩参数;N·m/A;Δi—两个线圈的差动电流；Jm—力矩马达衔铁及运动部分的转动惯量；θ—衔铁的角位移；Ba—衔铁的机械支撑和负载黏性阻尼系数；Ka—力矩马达衔铁转轴弹簧管扭转弹性系数；Km—力矩马达的磁弹簧刚度；TL—作用在衔铁上的负载力矩。

其中：Ki=2(a/g)NεΦε。

当力矩马达静止时，静态的力矩平衡方程为：

KiΔi=(Ka-Km)θ+TL

(2)

从式(1，2)可以看出：Ki是一个与结构尺寸、线圈匝数、永磁铁参数有关的参数，当结构尺寸固定时，永磁铁磁力越强，Ki越大。

Ka是弹簧管的刚度，用于平衡主动转矩，弹簧力矩大小与转角成正比。

Km是由磁力的特性产生的，转角越大，气隙越减小，吸力越大，与一个负弹簧等效，从控制角度来说不利于系统稳定，所以必须保证Ka>Km。

TL是力矩马达的负载转矩，主要是指反馈组件的弹力。

反馈杆下端随阀芯运动时，对衔铁组件产生使θ减小的弹力，是阻力矩，其大小与阀芯的位移xv有关：

TL=Kf(r+b)2θ+Kf(r+b)xv

(3)

式中：Kf—反馈杆的刚度;r—射流管喷嘴到衔铁组件回转中心的距离;b—反馈杆下端与射流管喷嘴的距离;xv—滑阀阀芯位移。

从参数的意义可以看出，力矩马达的失效主要有以下两种情况：

(1)零件损坏。如线圈断路或短路，则Δi=0，转角θ=0，伺服阀完全不能工作;弹簧管断裂，则Ka=0，此时，只有用反馈杆的弹力来平衡电磁力矩，力矩马达的特性完全改变，性能不可预测；

(2)零件性能下降。对于Ki和Km来说，其值除了与结构尺寸及线圈匝数有关外，主要与永磁铁的磁动势有关，永磁铁受过高温或低温影响，或是有大量铁屑附着，都会使其性能下降，使Ki和Km减小。

从式(2)来看，Ki和Km减小，输入相同的电流Δi，转角会变小，从而使输出流量减小。如果弹簧老化，Ka减小，则同样输入电流Δi，转角会增大，伺服阀输出的流量会偏大，同样改变了伺服阀原来的线性特性。

2.2 液压放大器失效分析

液压放大器由射流盘和射流板组成。其中,射流盘包括1个射流喷嘴、2个接收通道和1个回油腔。喷嘴由油源供油,2个接收通道则分别通至滑阀的两端,通过控制射流板的运动实现其流量变化,起到射流和接受液流的作用。喷嘴与挡板的间隙是最薄弱、最易污染的地方,若喷挡间隙或喷嘴堵塞污染,堵塞一侧,前置腔压力升高,会引起阀芯向另一侧运动,从而导致阀芯无法及时复位,表现为阀芯卡滞现象。

此外,在长期高速射流的冲击下,容易发生冲蚀磨损,造成控制腔输出压力的改变,进而影响电液伺服阀性能。

2.3 滑阀组件失效分析

作为伺服阀的功率输出级,滑阀组件由阀芯和阀套组成,直接将液压放大器的压力信号转换为阀的开口输出流量,同时通过反馈杆将阀芯位移反馈给力矩马达。阀芯作为引动部件,易受油液污染、泄漏量和静止时间的影响而卡滞。

一般情况下,大于阀芯间隙的颗粒很难进入滑阀副间隙,对滑阀工作很难造成危害;较微小的污染物进入滑阀副环形缝隙,会随着油液流出。但当油液较脏时,随着污染颗粒的聚积效应,污染物在滑阀副间隙不断聚集,致使阀芯运动摩擦力加大,阀响应时间延长,使阀变得不稳定[13]。阀芯和阀套在油液环境下进行往复运动,易发生表面划伤和磨损,影响伺服阀的性能,内漏增加,滞环增大。滑阀环形缝隙中不均匀的淤积会产生严重的侧载荷,侧载荷使得阀芯与阀套的金属接触表面之间出现微观粘附,中等卡涩会使摩擦力加大,严重的卡涩会造成滑阀副卡紧失效[14]。

大量流体机械系统故障是由于油污和液体环境差造成的[15],在分解检查的伺服阀中,从滑阀腔内冲出很多颗粒物。因此,导致电液伺服阀工作不正常的原因大多是油液污染度超标,较多肉眼看不到的污物会导致滑阀卡滞[16]。

2.4 反馈组件失效分析

反馈组件主要是指一端与阀芯中心固连,另一端与马达衔铁组件固连的金属杆件。反馈杆将阀芯位移以反馈力的方式反馈到马达衔铁上。反馈杆随着滑阀的往复弯曲运动,易发生疲劳断裂,影响伺服阀的流量输出。

通过FMMEA分析,电液伺服阀的主要故障模式有:力矩马达的弹簧管、反馈组件受力部件、液压放大器和滑阀组件等运动部件的磨损,线圈和密封件的老化。影响疲劳寿命的敏感应力为压力及负载,影响磨损寿命的敏感应力一般包括频率、行程和压力,影响老化寿命的敏感应力为温度。

3 电液伺服阀的寿命模型

3.1 产品寿命定义

产品寿命是指产品能够在固定工作条件、规定的可靠度置信范围内,完成规定功能的时间长度。为了评价产品寿命,需要建立可靠性和寿命[17]的关系,即产品寿命与产品的可靠度有关。

可靠度是关于工作寿命t的函数，可以用可靠度函数R(t)来表示。可靠度寿命就是指可靠度为给定值时的工作寿命，并以tR表示。

可靠度寿命有以下两种特别寿命：

(1)中位寿命。可靠度R=50%的可靠度寿命，称为中位寿命，用t0.5表示；

(2)特征寿命。可靠度R=36.8%的可靠度寿命，称为特征寿命，用te-1来表示，针对于威布尔分布，此时特征寿命te-1=θ。

3.2 可靠性与寿命的数学描述

可靠性函数R(t)的积分形式，可用故障密度函数F(t)来表示，即：

(4)

产品的寿命分布通常用概率论和数理统计的方法来描述。产品寿命预期值可用下式表示：

(5)

针对产品寿命，常用的分布函数有指数分布、威布尔分布等。依据电液伺服阀的故障机理[18]，其寿命模型采用威布尔分布来描述，威布尔分布函数可作为因疲劳、磨损及老化而引起的故障机理的寿命模型。

接下来，笔者对威布尔的寿命模型进行推导。

威布尔故障密度的分布函数如下：

(6)

式中：β—形状参数，表示曲线的形状；θ—尺度参数，表示曲线的集中趋势(当t=θ时，无论β值是多少，其故障率为63.2%；因此，θ也被称为特征值，有助于确定威布尔分布的中心)；δ—初始位置参数，在寿命分析中，一般δ=0。

当δ=0时，式(6)可简化为：

(7)

根据式(7)，可以得到威布尔分布的R(t)，λ(t)的函数分布，如下式所示：

(8)

(9)

由式(8)可知，威布尔分布的可靠寿命为：

(10)

当β=1时，威布尔分布就变为指数分布，平均寿命就变为MTBF=θr(2)=θ，可靠寿命变为tR=-θ(lnR)。

因此，指数分布是威布尔分布β=1的特例，所以在不清楚元件的失效概率密度函数时，可统一用威布尔分布模型来表示指数分布模型和威布尔分布模型。

4 电液伺服阀的寿命分析

依据电液伺服阀的结构组成原理,力矩马达、液压放大器、滑阀组件和反馈组件的功能紧密关联,任何一环出现故障,都会影响电液伺服阀的性能,导致任务无法完成。因此,各部件的可靠性是串联的关系。

依据其功能层次,笔者建立了电液伺服阀的可靠性框图,如图2所示。

图2 电液伺服阀的任务可靠性框图

再依据电液伺服阀可靠性框图，建立由各零部件R1(t)、R2(t)、R3(t)和R4(t)串联混合的可靠性模型。

产品可靠度数值等于各零部件可靠度数值的乘积，则产品可靠度为：

(11)

式中：Ri(t)—t时刻第i零部件的可靠度。

各零部件的可靠度R(t)一般不是一个定值，而是服从不同函数分布的。在不清楚元件的失效概率密度函数时，可统一用威布尔分布模型来表示。

当威布尔分布的形状参数为2时，它被称为Rayleigh分布，其应用广泛，此分布可广泛用于电真空设备的寿命检验中。在产品的寿命期间，磨损失效风险不断增加。通过调整威布尔分布的形状参数β，可以对许多不同寿命分布的特征进行建模[19]。

当0<β<1时，早期失效发生在产品寿命的初始阶段。这些失效可能会迫使产品进入“老化”阶段，以降低初期失效的风险；

当β=1时，失效率保持恒定。随机失效，失效的原因有多种；

当β=1.5时，属于早期磨损失效；

当β=2时，在产品的寿命期间，磨损失效风险不断增加，此分布可广泛用于电真空设备的寿命检验；

当3≤β≤4时，属于快速磨损失效；

当β>10时，属于非常快的磨损失效。

假设电液伺服阀的力矩马达和液压放大器失效模型均满足β=2的威布尔分布，滑阀组件和反馈组件均满足β=1的威布尔分布，则产品的可靠度可表示为：

(12)

式中：θ—特征寿命参数，与失效率参数λ相关，单位为小时。

根据产品现有故障数据和寿命试验数据，按照不同应力类型，笔者对产品寿命与应力大小之间的关系进行分析，建立可靠性寿命模型[20]。

在可靠度为R(t)时，产品的寿命为tR：

(13)

笔者将求出的特征值θ以及各零组件的形状参数β和失效率λ代入式(8)中；并从t=0开始逐渐增加到t=tend，每增加一次，可以分别得到力矩马达、液压放大器、滑阀组件、反馈组件的可靠度函数R1(t)、R2(t)、R3(t)和R4(t)；然后，根据式(12)求出此刻的电液伺服阀可靠度Rs(t)，直至计算结束。

由此可以得出电液伺服阀的可靠度[21]随时间变化曲线,如图3所示。

图3 电液伺服阀可靠度变化曲线与工作寿命

当t=t1时，可靠度Rs(t)即为电液伺服阀工作时间为t1时的可靠度，即若需确定电液伺服阀可靠性下降到某一值Rs(tR)时所得最低可靠度，对应的计算时间则为产品可靠寿命tR[22]。

由图3可知：当可靠度为0.73时，电液伺服阀寿命为t0.73=30 000 h；当可靠度为0.9时，对应的寿命t0.9=12 477 h。

5 结束语

现有的研究中,针对电液伺服阀故障模式及失效机理分析得较少,完整的电液伺服阀寿命评估方法研究存在不足,为此,笔者提出了一种基于故障模式及失效机理分析(FMMEA)的电液伺服阀寿命分析方法。

首先,以电液伺服阀为研究对象,通过对电液伺服阀进行故障模式及失效机理分析(FMMEA),确定电液伺服阀耗损机理和寿命特征;然后,依据现有的故障数据及应力类型,建立电液伺服阀寿命预测模型,并对其进行寿命评估;最后,建立电液伺服阀可靠性模型,并进行电液伺服阀的寿命分析。

研究结果表明:

(1)通过统计、试验、分析、预测等方法获得了产品的故障模式,从国内外标准、手册中获取了失效率数据,可以较为方便地确定电液伺服阀的耗损机理和寿命特征;

(2)依据电液伺服阀现有的可靠性数据,合理选取了威布尔模型的形状参数,建立了电液伺服阀关键部件的较为准确的寿命预测模型,有利于对电液伺服阀的寿命进行评估,提高了各种因素影响下电液伺服寿命分析的准确性。

在后续的工作中,笔者需要对电液伺服阀各个零件的具体失效模式及机理进行详细分析,通过积累更多故障数据,更加准确地选取多个工况下寿命预测模型中的形状参数,提高电液伺服阀在多个工况下的可靠性分析的准确性。