基于正交实验方法的电磁阀响应特性分析*

王洪波,黄智鹏,王娜娜,任 旺,徐悦鹏,俞 滨,孔祥东

(1.航空工业庆安集团有限公司,陕西 西安 710077;2.燕山大学 机械工程学院,河北 秦皇岛 066004)

0 引 言

用于某系统的电磁阀,通常都是通过线圈的通电或断电,以此来实现刹车的开启或释放。因此,电磁阀的响应特性直接影响舱门系统的性能。经分析可知,影响电磁阀响应特性的因素有很多,比如工作气隙、安匝数、动质量、弹簧刚度[1-5],等等。

为了优化电磁阀的响应特性,国内外学者都进行了大量的研究。为了提高换挡控制系统的性能,Xu Xiang-yang等人[6]对直动电磁阀进行了建模和动力学分析,分析结果表明,减小阀芯与滑套之间的间隙可以延长直动电磁阀的压力响应时间。柴玮锋等人[7]通过搭建电磁铁仿真模型,研究了电磁铁极靴凸起高度对电磁铁初始吸力及力位移特性的影响,并得到了极靴凸起高度最优值。范玉等人[8]研究了低刚度弹簧预紧力与刚度,高刚度弹簧刚度、高刚度弹簧端面与衔铁的初始间隙,对电磁阀动态响应特性的影响,并得出了结论,即相较于单弹簧的情形,双复位弹簧的设计可以同时优化电磁阀的开启和关闭响应特性。邹开凤等人[9]提出了一种自行设计的基于电容放电的驱动电路,并通过仿真研究,确定了该驱动电路参数的取值范围,通过仿真试验的方法,研究了电磁阀线圈结构参数对响应特性的影响;仿真和试验结果表明,该电磁阀具有较好的动态响应特性。

传统的设计方法主要是利用经验公式与样机试验方式进行设计,缺少多方案的对比和优化,无法实现多参数的匹配分析,同时不能满足民机的研制周期短、成本低等要求[10]。而利用计算机进行建模仿真则可以大大地提高研制的效率。

为了优化多变量相互作用下电磁阀的动态响应特性,李红等人[11]采用AMESim软件建立了一款常开电磁阀模型,分析了其阀芯的动作机理,利用开关电磁阀响应测试台,验证了所建模型的有效性;并且借助变量控制法,探讨了结构参数对电磁阀阀口流量特性的影响,提出了一种基于试验设计-遗传算法的优化方法,用于处理多变量交互作用下,电磁阀的响应特性优化问题。何志壮等人[12]利用AMESim仿真软件,建立了电磁脉冲阀的系统仿真模型,得到了双压控制改进方案,能够有效地减少电磁阀出口气压的响应时间,并节省电磁阀关闭时间。针对电磁阀开启和关闭响应时间相互影响的问题,基于Maxwell,李京骏等人[13]建立了电磁阀的瞬态场三维模型,对影响电磁阀性能的关键因素进行了仿真研究,得到了增大弹簧刚度会使电磁阀上升时间和关闭响应时间延长的结论。

为了解决电磁阀发热量较大的问题,吴柳杰等人[14]提出了一种变电压控制方法,可以保证电磁阀长时间地正常工作,有效提高了电磁阀的工作性能。

由于影响电磁阀响应特性的因素众多,如果进行电磁阀响应特性的全面测试,工作量较大。在不影响测试效果的前提下,为了减少测试的次数,可以采用正交实验法。

正交实验设计法是解决多因素、多水平实验问题的一种优化设计技术。它利用正交表进行实验方案的最优设计,以寻找实验的优化方案。正交实验设计法目前得到了广泛的应用。曹年欢等人[15]应用水平正交实验法进行了隧道除尘喷嘴设计。Zheng Tao等人[16]通过多因素正交和优化实验,制备了轻质泡沫磷石膏材料。LIU Wen-fei等人[17]采用正交试验设计和Ga-BP算法,对敞车车体箱形梁进行了优化。LIU Ting等人[18]采用了正交实验优化聚丙烯酰胺凝胶路线,制备低电阻率氧化铟锡纳米粉体。

综上所述,目前有关电磁阀响应特性的大量研究都是对各个电磁阀响应特性的影响因素进行单独的分析,并没有对各因素进行组合分析,而且对影响电磁阀响应特性因素的主次顺序的研究也较少。

为此,笔者对影响电磁阀响应特性的主要影响因素进行组合分析,同时为较大程度地提高其研制的效率,利用计算机建立电磁阀的仿真模型,应用正交实验法,以此来寻找影响电磁阀响应特性参数的最优组合方案。

1 电磁阀仿真模型

电磁阀主要由钢球式液压阀和电磁铁组成。电磁铁是电磁阀的驱动部件,将电能转换为磁场能,产生电磁力,推动阀的活动部分动作,实现阀的液压功能转换;液压阀是电磁阀的执行部件,实现阀的连接和液压油路的转换;顶杆实现两部件的关联。

电磁阀结构原理图,如图1所示。

图1 电磁阀结构原理图

当收到系统指令后,电磁阀通过通电和断电进行油路位置的切换,从而控制功能转换阀进行转换,进而控制系统整个油路的通断,最终实现对舱门的收放控制任务。

综上所述,由于电磁阀是电、磁、机械-液压结合体,笔者建立其仿真模型的电路系统仿真模型、磁系统仿真模型和机械-液压系统仿真模型。

1.1 电磁阀工作原理

电磁阀的工作原理,如图2所示。

图2 电磁阀工作原理图

由图2可知:

当电磁阀线圈通电时,电磁线圈产生电磁力,电磁铁的吸力和进油压力的合力克服弹簧力,推动衔铁向左运动,阀芯随之向左运动,进油口和出油口接通;

当电磁阀线圈断电时,电磁力消失,弹簧力克服进油压力,推动阀芯向右运动,出油口和泄油口接通。磁芯的运转将控制流体在阀体的通断,以达到改变流体方向的目的。

1.2 电磁阀数学模型

在电磁阀方案设计中,作为仿真模型的初始输入,电磁阀已知参数如表1所示。

表1 电磁阀已知参数

1.2.1 电路系统模型

电路系统的作用是将输入的电压转变为激磁电流。电磁阀的铁芯线圈具有一定的电感,线圈中的磁通会阻止电流增长,让其按指数曲线的规律增长到稳定值。

其静态等效电路数学模型如下:

(1)

式中:u—电路的驱动电压;R—线圈电阻;L—线圈的电感;ψ—磁链;t—时间。

1.2.2 磁系统模型

电磁部分是实现电磁转换,产生电磁力,是电磁阀的动力驱动部分。

根据基尔霍夫磁压定律,其磁路计算数学模型如下:

I·W=Fz=Fq+Fd=φ(Rq+Rd)

(2)

(3)

式中:I·W—安匝数;Fz—总磁势;Fq—气隙磁势;Fd—导磁体磁势;φ—磁通量;Rq—气隙磁阻;Rd—导磁体磁阻;G—磁导;X—工作气隙;Fx—电磁吸力。

1.2.3 机械系统模型

机械系统的作用是将电磁能转换为机械能而使衔铁运动。线圈通电产生电磁力,克服弹簧力、摩擦力,使衔铁运动,反之亦然。

根据达朗贝尔运动方程、衔铁运动方程,可以得到系列方程,其中,电磁阀通电状态运动方程为:

(4)

电磁阀断电状态运动方程为:

(5)

弹簧力为:

Fs=K(x0+x)

(6)

摩擦力为:

(7)

式中:Fp—液压力;Fs—弹簧力;Ff—摩擦力;CV—速度阻尼系数;Cf—油液的黏性阻尼系数。

由于线圈的通电、断电状态不同,式(4,5)中的力数值也会不同,具体数据需要在计算的时候进行考虑。

另外,笔者也考虑到了两种主要的摩擦力:(1)衔铁与线圈骨架之间相互运动而产生的动摩擦力;(2)衔铁与液压油之间摩擦产生的黏性阻尼力。以上二种摩擦力都与衔铁的运动速度成正比。

1.3 电磁阀整体仿真模型

根据电磁阀的数学模型,笔者采用常值模块、延时模块、插值模块、开关模块、积分模块,搭建了电磁阀的整体仿真模型,如图3所示。

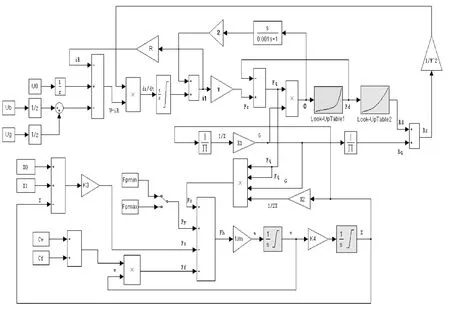
图3 电磁阀仿真模型

图3中的电磁阀仿真模型主要包括3部分,即电系统仿真模型、磁系统仿真模型和机械系统仿真模型。

2 电磁阀响应特性仿真优化

2.1 响应特性的正交表确定

影响电磁阀响应特性的因素众多,如工作气隙、弹簧刚度、动质量、工作行程等。其中,弹簧刚度、动质量、工作行程属于机械部分影响因素,线圈安匝数属于电磁部分影响因素。

电磁铁线圈匝数越多,通过线圈的电流越大,电磁力就越强。由式(2,3)可知,电磁力与安匝数成正相关,在设定输入直流电压恒定为28 V的情况下,由欧姆定律可知安匝数恒定,则优化线圈匝数,兼顾考虑线圈匝数对驱动电流的影响是必要的。

已有的研究结果表明[19]:电磁力随驱动电流的变化,取决于电磁阀总磁阻和驱动电流范围,当电流小于某值时,驱动电流是电磁力增加的主要因素;当电流大于这个值时,总磁阻成为制约电磁力增加的决定因素。这是因为电磁阀总磁阻对电磁力降低的贡献率随线圈匝数增加而增大。当匝数变化时,驱动电流作为因变量也相应改变为特定值。

故笔者采取把线圈匝数作为优化变量,以此来分析安匝数恒定情况下,线圈匝数与驱动电流的共同作用对响应特性的影响。

弹簧力是电磁力的一种反力。增加弹簧预紧力可以使电磁阀的吸合时间延长,关闭时间加快。工作行程变化,则动铁芯与线圈骨架之间的摩擦面积也会随之变化,从而影响电磁阀的吸合时间和释放时间。对动铁芯进行减重处理,可以提高其运动的反应速度,进而优化电磁阀的响应特性。

根据以上分析,笔者确定4个影响因素,即A(匝数)、B(弹簧)、C(工作行程)和D(动质量);并且,每个影响因素包括有3个水平,分述如下:

根据外形尺寸和电阻要求,选取匝数A的3个水平分别为:1 990匝、2 000匝、2 010匝;

根据结构尺寸和液压力,选取弹簧刚度B的3个水平分别为:21 N/mm、22 N/mm、23 N/mm;

根据钢球行程的实际尺寸,选取工作行程C的3个水平分别为:0.22 mm、0.26 mm、0.3 mm;

根据结构强度和磁靴截面积影响,选取动质量D的3个水平分别为:1/57 kg、1/67 kg、1/77 kg。

根据不同参数组合仿真,笔者得到了吸合时间与释放时间结果,如表2所示。

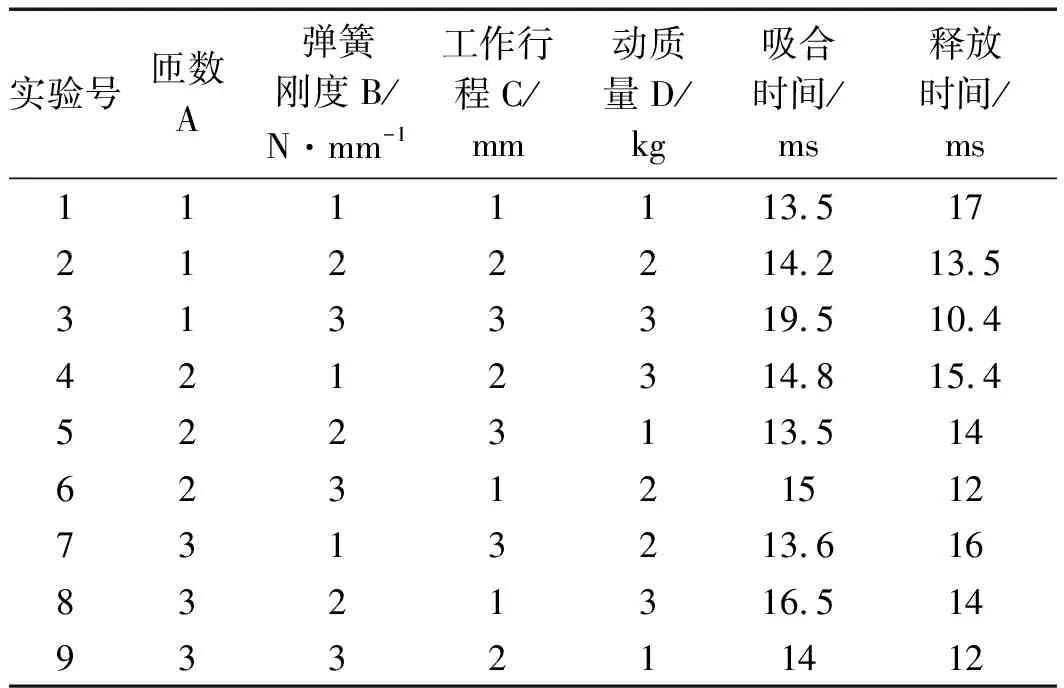
表2 正交表L9(34)

2.2 优化仿真方案的确定

按照正交表规定的方案,笔者应用Simulink仿真软件进行仿真分析,并采用极差分析法,对基于正交实验方法的仿真结果进行分析,得出影响因素的主次顺序和优化方案,如表3所示。

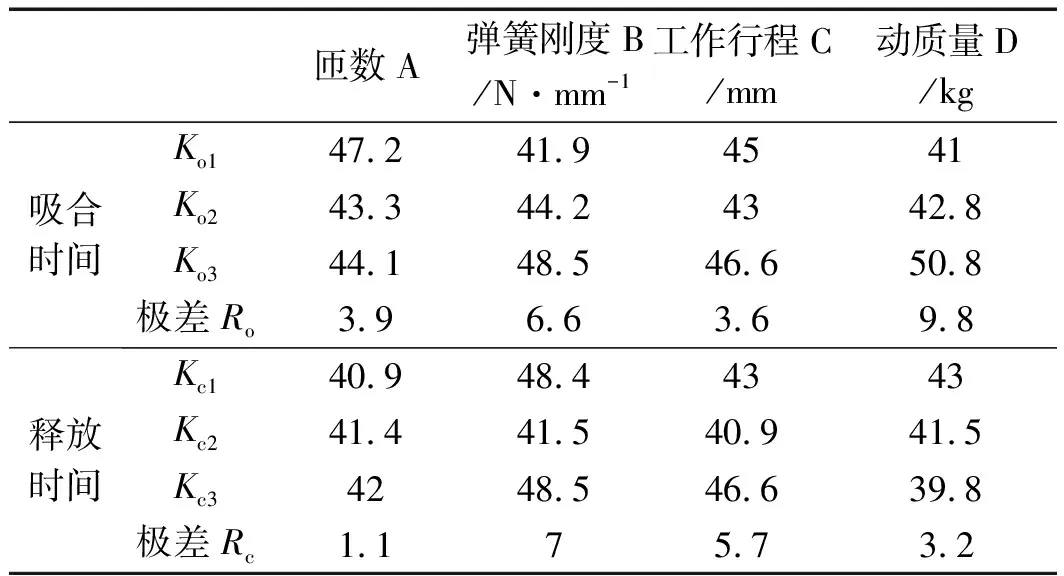
表3 仿真实验方案及结果分析

2.2.1 因素对响应特性的影响分析

各因素水平对电磁阀响应特性的影响中,对吸合时间的影响如图4所示。

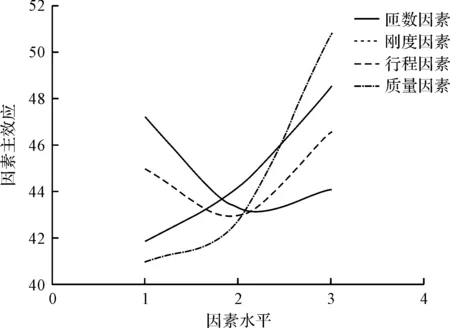
图4 不同因素水平对吸合时间的影响

不同因素水平对释放时间的影响如图5所示。

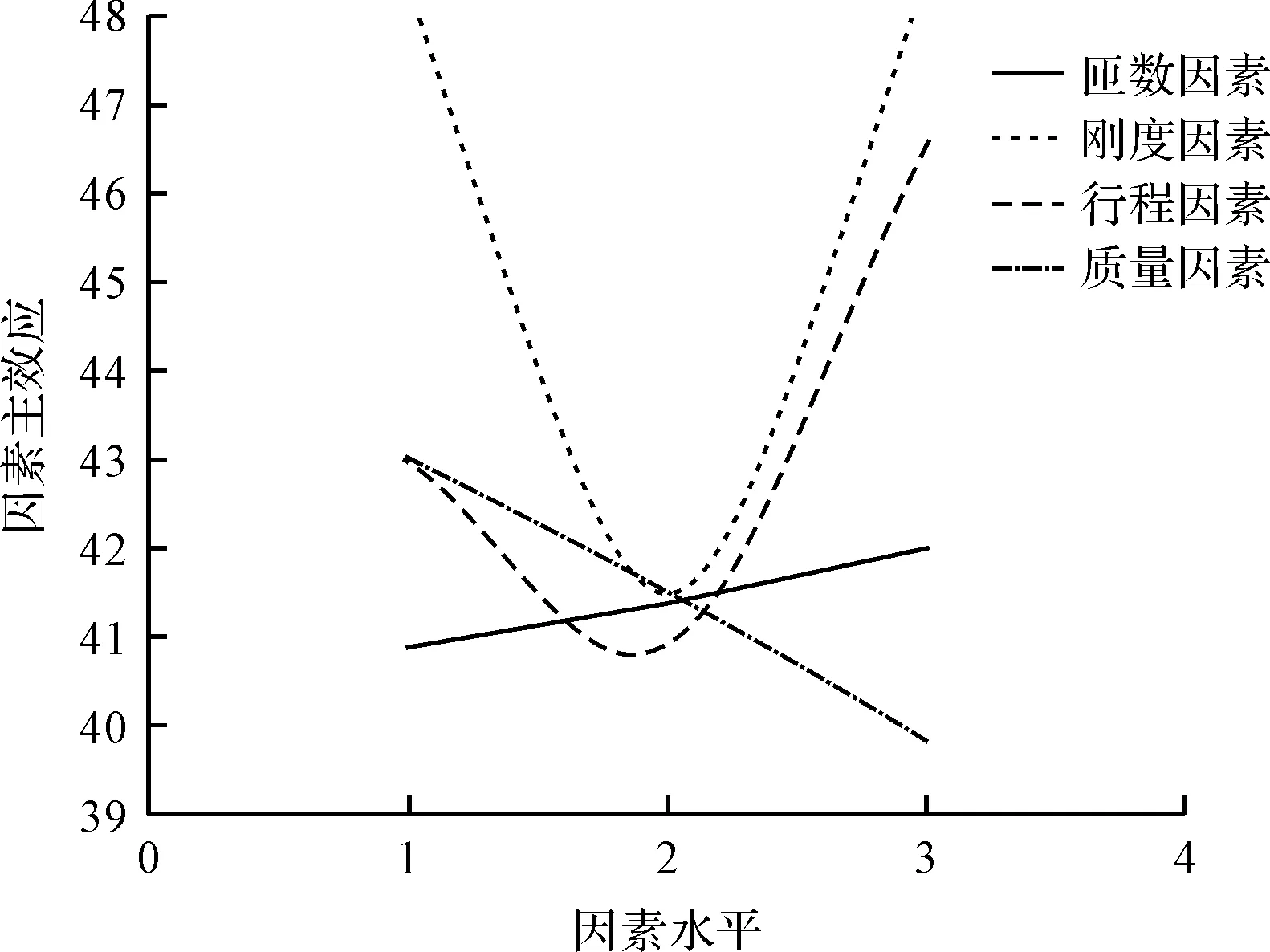
图5 不同因素水平对释放时间的影响

随着匝数的增加,吸合时间呈先减小后增大的趋势,而释放时间随着匝数的增加而增加,因此,兼顾吸合时间和释放时间,匝数应该有一个最优值;

随着弹簧刚度的增加,吸合时间增加,而释放时间先减小后增加,因此,需要根据时间的要求值,统筹考虑刚度的取值;

随着工作行程的增加,吸合时间和释放时间都是先减小后增加;随着动质量的减小,吸合时间增加,释放时间减小。

综合考虑各因数水平对响应特性的影响,进行因素影响程度的排序和最优方案的确定。

2.2.2 因素主次顺序的确定

表3中,主效应KOi与Kci表示各因素在3个水平下仿真得到的吸合时间和释放时间的总和;极差Ro与Rc为各主效应之间的最大差值,极差越大说明该因素水平的响应特性的影响越大,极差最大的因素水平对响应特性的影响最大,也就是最主要的因素。

分析表3极差值可知:影响电磁阀开启特性的因素的主次顺序依次是动质量、弹簧刚度、匝数、工作行程;影响释放响应特性的因素的主次顺序依次是弹簧刚度、工作行程、动质量、匝数。

2.2.3 优化仿真方案的初步确定

各因素水平的确定与指标有关。如果指标越小越好,则应选取指标小的那个水平,反之亦然。

笔者以综合考虑吸合时间和释放时间最小的仿真结果为最优;最佳组合是A3B3C1D2,即:电磁阀的匝数为2 010匝、弹簧刚度23 N/mm、工作行程0.22 mm、动质量1/67 kg。

3 优化方案分析与验证

笔者采用最优组合方案A3B3C1D2,应用Simulink仿真模型进行仿真分析,提取到的瞬态仿真结果如图6所示。

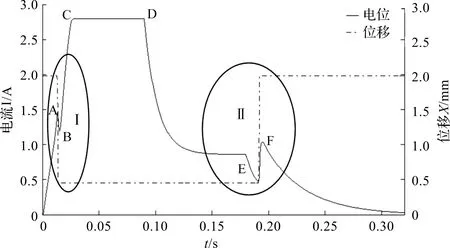
图6 电磁阀最优方案仿真结果

由于电磁阀的铁芯线圈具有一定的电感值,加上电压后,线圈电流从零上升,磁通Φ也随之增加。磁通的增长在线圈中产生感应电动势,它总是阻止电流的增长,所以电流不会在接通电源的一瞬间跃变到稳定值,而是按指数曲线的规律增长到稳定值[20]。

图6表明了电磁阀从接通到断开过程中,线圈电流和衔铁位移分别随时间变化的趋势。

电磁阀断电后,电磁阀线圈可以认为是一个电感元件,它有阻碍电流下降的趋势。现假设线圈电阻为R,电感为L,因为断电后其电压为零,电流下降的规律应该满足公式:

(8)

Φ=iL,为穿过线圈的磁通,由式(8)可得:

(9)

图6中的DE段阀芯尚未动作,该过程线圈电感L保持不变,即dL/dt=0,DE段电流方程为:

(10)

对式(10)进行积分后,可得到DE段电流与时间关系为:

(11)

这便是DE段电流随时间的变化关系,为一指数下降曲线。

因为电磁阀是一含铁芯线圈,当电流下降到E点附近时,阀芯开始动作,这时线圈电感L不再是个常数,它随阀芯与挡铁之间的气隙变化而变化。

设阀芯与挡铁之间的气隙为X,沿阀芯释放方向为正方向。工作气隙的磁阻R可表示为:

(12)

因为导磁体磁阻相对工作气隙的磁阻较小,可认为工作气隙的磁阻就是线圈磁阻,所以线圈电感随气隙变化的关系式为:

(13)

式中:μ0—真空磁导率;S—阀芯横截面积;N—线圈匝数;X—工作气隙。

由式(9,13)可得:阀芯动作后的电流变化方程为:

(14)

其中,K=μ0N2S。

现假设可以使阀芯任意运动以维持电流不变,即di/dt=0,根据式(14),可得:

(15)

阀芯运动状态如果能满足式(15),那阀芯运动产生的反电动势可以维持电流不变。这就是电流曲线出现极值(波峰)的条件。

吸合过程放大图如图7所示。

图7 吸合过程放大图

图7直观地反映了电磁阀的吸合过程,即当线圈通电后,电流按指数上升至吸合电流值a点后,吸力增至与阻力相同大小,衔铁开始运动,由于运动引起电感发生变化,产生反电动势,这个反电动势会阻止电流上升,所以运动过程电流不但不继续上升,反而逐渐下降,工作气隙逐渐减小,至拐点最低点b时衔铁停止运动,电磁阀完全打开,开启时间为从0点(开始通电)至b点(衔铁运动至闭合位置)时间段,即14 ms。

释放过程放大图如图8所示。

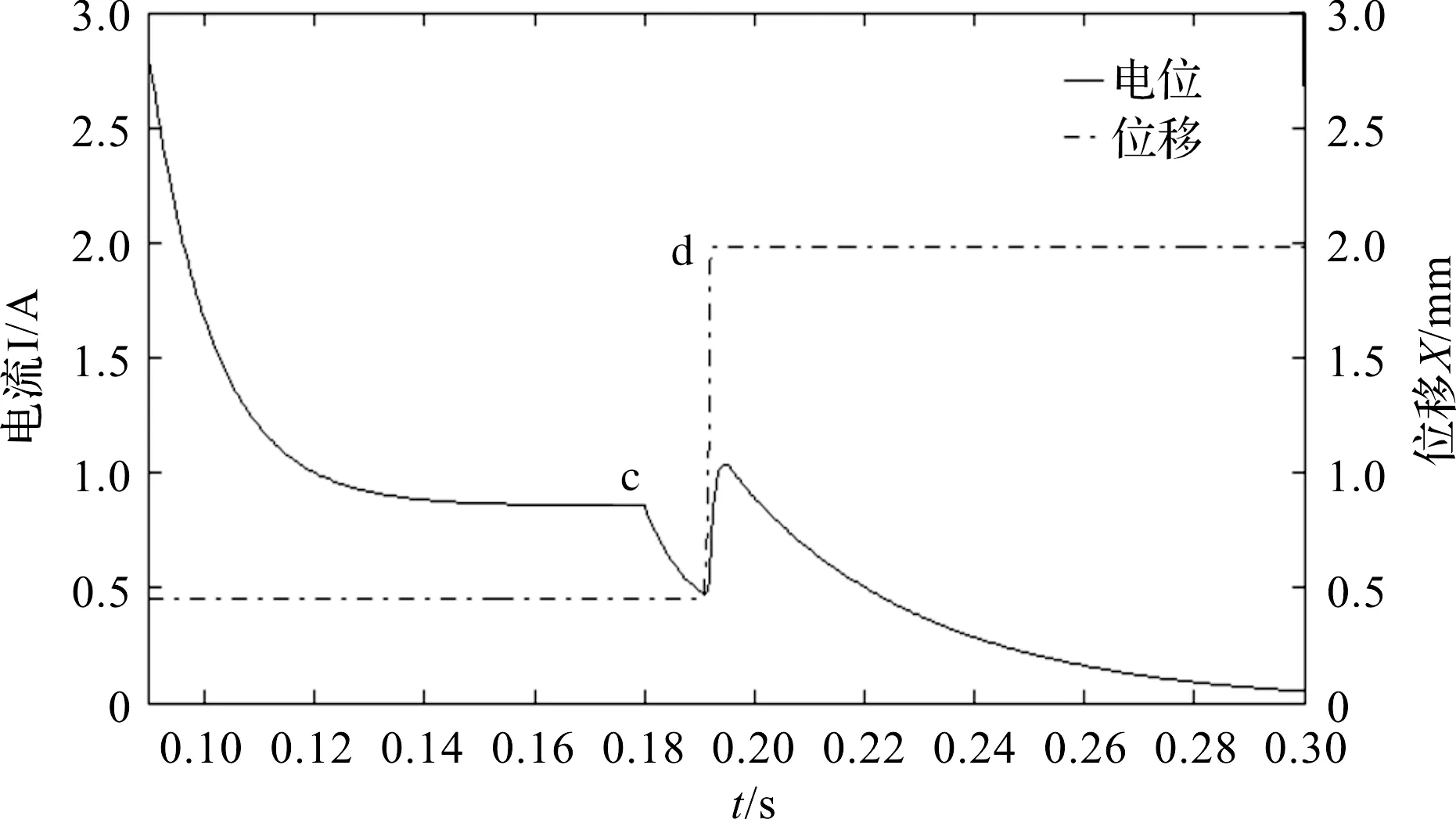
图8 释放过程放大图

图8直观地反映了电磁阀的断开过程,即当输入电压降至c点后,衔铁在复位弹簧的作用力下开始返回,至拐点d运动至初始位置,电磁阀完全释放,释放时间为从c点(断电)至d点(衔铁返回至初始位置)时间段,即12 ms。

最优组合方案的吸合时间14 ms,释放时间12 ms。与表2中其他参数组合以及优化前参数的响应特性(吸合时间:25 ms,释放时间20 ms)相比,在最优组合条件下的实验结果响应特性得到了明显改善,能够满足设计要求。由此可以证明该方案是可行的。

4 结束语

为了优化电磁阀的响应特性,笔者以某系统用电磁阀为研究对象,基于Simulink软件建立了电磁阀的电、磁、机械-液压仿真模型,并利用正交实验方法,对开关电磁阀的响应特性进行了仿真,为提高电磁阀的响应特性提供了理论支撑,得出的结论如下:

(1)影响开启特性因素的主次顺序依次是动质量、弹簧刚度、匝数、工作行程;影响释放特性因素的主次顺序依次是弹簧刚度、工作行程、动质量、匝数。最优组合方案下的响应特性与优化前相比得到显著提高;

(2)影响电磁阀响应特性需要考虑的影响因素众多,进行全面测试工作量较大,所以应用正交实验法解决多因素实验的问题,可以使用最少实验次数找到最优方案,大大提高其设计效率。

在目前的研究中,笔者只是基于影响电磁阀响应特性的主要因素进行了优化分析,因此,该结果具有一定的局限性。

在后续的研究中,笔者将根据需要对电磁阀更多参数进行更全面深入的优化分析。