基于等时距处理和IOWHA算子的路基沉降预测

邱红胜， 杨雨， 李东健， 罗刚

(武汉理工大学交通与物流工程学院， 武汉 430063)

软土作为特殊土的一种尤为常见，江河中下游、湖泊以及沿海地区附近均有软土覆盖，因软土具有强度低、压缩性高、承载力低、易于扰动等不良工程特性，直接计算沉降是有一定难度的，因此技术人员常根据现场实测数据推测沉降量[1]。

大量工程经验表明，全过程的地基沉降与时间的关系曲线呈S形[2]，路基的沉降过程经历发生、发展、成熟、到达极限4个阶段[3]。由于S形曲线能很好地描述路基固结沉降的发展规律，因而近年来受到各国学者青睐。张宇亭等[4]用Gompertz模型对滨海路基进行沉降预测，将预测值与实测值比对，证实该方法在软土地基沉降预测的可行性。朱志铎等[5]验证了实测沉降曲线与Logistic曲线基本吻合，表明用于拟合的数据越多预测结果越精准。胡习阳等[6]建立GM(1,1)、灰色Verhulst和非等时距UGM(1,1)3种模型进行沉降预测，结果表明灰色Verhulst模型模拟和预测精度更高。

影响软土路基沉降的因素有很多，单一的预测模型和预测方法不同发展阶段的精确性和适用性不同，即便对单一模型进行改进，预测结果的可靠性难以保证。而组合预测将不同的预测方法进行适当组合，能够综合各单项模型优势避免单一预测模型受随机因素的影响，进而有效提高预测精度[2-3,7- 8]。王博林等[9]通过建立Gompertz和Logistic模型以及二者的最优化组合模型对高填方土体后期沉降量进行预测，结果表明最优组合模型的精度和可靠性均优于单一模型。刘光秀等[10]通过对灰色模型和Gompertz模型根据最优加权组合原理建立组合预测模型，验证了新构建的组合模型能够有效消除系统误差提高拟合精度。王俊瑜等[11]基于三参数幂函数模型和Logistic模型，以最小误差平方和为准则构建了最优组合沉降预测模型，发现组合模型拟合结果可靠，预测精度明显高于单项模型。

根据上述研究成果，选用Gompertz、Logistic和灰色Verhulst 模型3种模型为单预测模型，分别以原始沉降数据、经过三次样条插值处理的数据和经过分段三次插值处理的数据为样本值建立3种单模型，经过对比分析得到每种模型的优势方法。对3种单模型建立基于诱导有序加权调和平均(induced ordered weighted harmonic averaging，IOWHA)算子的组合预测模型，并用遗传算法(genetic algorithm，GA)和MATLAB的非线性优化工具箱两种求解方法。

1 单预测模型及等时距处理方法简介

1.1 S形曲线简介

Gompertz模型最初用来描述自然界生长变化的规律，之后Gompertz曲线广泛应用于在市场经济和交通预测中，其预估模型的表达式为

sg=Le-ae-bt

(1)

式(1)中：L、a、b为模型3个待定参数；t为时间；sg为Gompertz曲线的预测沉降量。

Logistic曲线是以美国生物学家和人口统计学家Raymond Pearl名字命名的曲线，可以反映生物生长过程，被广泛应用于生物繁殖和产品生命周期分析等方面，目前也被应用于路基沉降预测中，其预估模型的数学表达式为

(2)

式(2)中：sl为Logistic曲线的预测沉降量。

运用Origin软件对Gompertz和Logistic两种S形曲线模型进行拟合，用拟合优度R2评价拟合程度，R2取值范围为0～1，R2越接近1说明拟合效果越好。

1.2 灰色Verhulst预估模型

1.2.1 模型建立

灰色Verhulst模型主要用来描述具有饱和状态的演化过程，如S形过程，反映了生物生长由加速到减速增长到最终趋于稳定的过程，这一过程和路基沉降基极为相似。

灰色Verhulst模型的表达式和灰色Verhulst模型的白化方程分别为

S(0)(k)+aZ(1)(k)=b[Z(1)(k)]2

(3)

(4)

式中：S(0)为原始沉降数据序列；k=2,3,…,n；S(1)为S(0)的1-AGO序列；Z(1)为S(1)的紧邻均值生成序列。

白化方程的解为

(5)

灰色Verhulst模型的时间响应式为

(6)

Verhulst模型的参数用最小二乘法估计表示为

(7)

式(7)中：

(8)

(9)

1.2.2 模型的精度检验

后验差检验是最灰色预估模型常用的检验方法。检验步骤如下。

步骤1计算原始时间序列S(0)的均值和方差，其表达式分别为

(10)

(11)

步骤2计算残差数列e0={e0(1),e0(2),…,e0(n)}的均值和方差，计算公式分别为

(12)

(13)

步骤3计算后验差比值，其计算公式为

c=s2/s1

(14)

步骤4计算小误差频率，其计算公式为

p=|A|/n

(15)

步骤5根据表1判定预测精度的等级。

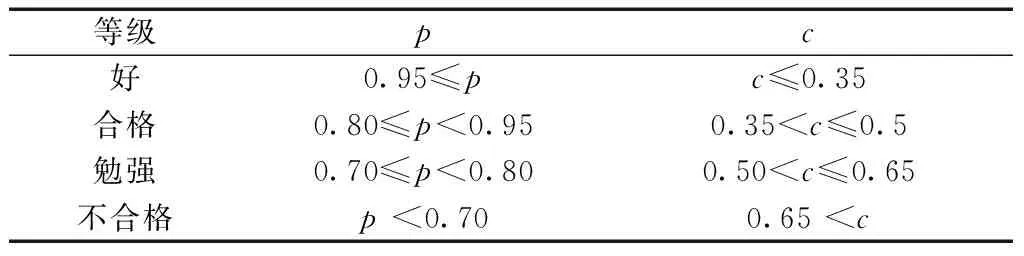
表1 模型预估精度检验等级Table 1 Test scale of model prediction accuracy

1.3 等时距处理方法简介

1.3.1 分段三次Hermite插值

在实际中不仅要求插值在节点的函数值相等，同时要满足节点导数值相等，甚至要满足高阶导数值相等，满足这种要求的插值多项式称为Hermite插值多项式。构造的插值多项式的次数过高可能会出现龙格现象，因此采用分段插值的方法构造多项式。设函数f(x)在[a,b]上的节点xi处函数值为yi(i=0,1,…,n)，导数值为mi(i=0,1,…,n)，对任意两相邻节点xk、xk+1(k=0,1,…,n-1)可构造两点三次埃尔米特插值多项式，可表示为

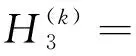
k=0,1,…,n-1

(16)

(17)

分段三次Hermite插值多项式为

(18)

因此分段线性插值函数Ih(x)在[a,b]上用插值基函数表示为

(19)

式(19)中：

(20)

(21)

则余项可表示为

|R3(x)|=|f(x)-Ih(x)|

(22)

式(22)中：

(23)

式(23)中：f(4)(ξ)为f(x)的四阶导数在ξ处的函数值,ξ∈[xk,xk+1]。

1.3.2 三次样条插值

若函数P(x)∈[a,b]，在区间[xi,xi+1]上是三次多项式，x0,x1,…,xn是区间[a,b]上的节点，则称P(x)为节点x0,x1,…,xn上的三次样条函数。若yi=f(xi)(i=0,1,…,n)是在节点xi上给定的函数值，且满足P(xi)=yi(i=0,1,…,n)，则称P(x)为三次样条插值函数。P(x)需满足式(24)的条件，mi(i=0,1,…,n)为节点上的导数值。Pk(x)为[xk,xk+1]上的两点三次样条插值多项式，满足式(25)，令hk=xk+1-xk,k=0,1,…,n-1，整理后得到基本方程组如式(26)所示。

(24)

i=k,k+1；k=1,2,…,n-1

(25)

λkmk-1+2mk+μkmk+1=gk

(26)

插值函数不仅要满足中间节点的限制要求，也要满足下述边界条件。

(27)

当满足第一类边界条件时，基本方程组可简化为式(28)，矩阵形式如式(29)所示。

(28)

(29)

当满足第二类边界条件时，基本方程组可简化为式(30)，矩阵形式如式(31)所示。

(30)

(31)

2 组合预测模型的建立

2.1 基于IOWHA算子的组合模型权重系数的确定

利用MATLAB中的最优化工具箱计算得到基于IOWGA的组合预测模型的最优权系数。

基于IOWHA算子的组合预测模型克服了传统加权调和平均组合预测方法赋权的缺陷，综合考虑了每个单项预测模型在各个时间点的预测精度的高低按顺序赋权。

第t时刻IOWHA组合预测值可表示为

IOWHAL(〈p1t,s1t〉,〈p2t,s2t〉,…,〈pmt,smt〉)=

(32)

式(32)中：pit为第i种预测方法第t时刻的预测精度；sit为第i种预测方法第t时刻的预测值i=1,2,…，m；t=1,2,…,N；li为m种单项预测序列在组合预测种的加权系数(满足非负性和归一性)；sp-index(it)为预测精度第i个大的预测值。

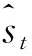
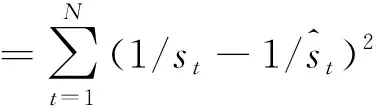
(33)

基于IOWHA算子的组合预测模型可表示为

(34)

式(34)中：L为由权重系数构成的列向量，L=[1, 2,…,m]。

2.2 组合预测模型评价标准

为反映基于IOWHA的组合预测模型的有效性，按预测效果的评价原则，选择误差平方和、均方误差、平均绝对误差和平均绝对百分比误差作为评价指标，如式(35)所示，这4项指标值越低表明模型预测精度越高。其中MAPE的精度分级原则如表2所示。

(35)

式(35)中：SSE为误差平方和；MSE为均方误差；MAE为平均绝对误差；MAPE为平均绝对百分比误差。

表2 MAPE预测精度等级划分Table 2 MAPE classification of prediction accuracy

3 等时距处理方法对比研究

3.1 常张高速公路软土路基

常张高速公路K159+585是一典型观测断面[2]，原地基为软土地基，土质为低液限黏土，施工进行了粉喷桩处理。高路堤填土为红砂岩，设计填方高度为15.1 m，观测板板底距原地面1.392 m，主要观测原地基的沉降量。

为提高模型预测精度，通过对样本值的比选，适当剔除观测前期数据，以351 d以前的观测数据作为各预测模型的样本值，对351～409 d共58 d的4期数据进行预测。Gompertz模型和Logistic模型以166～341 d的观测值作为样本值，灰色Verhulst模型以184～341 d的观测值作为样本值。

根据第2节中所述的分段三次Hermite插值和三次样条插值求解方法，分别对3种单一预测模型进行处理得到等时距的沉降数据样本值。对原始观测沉降值以及两种等间距处理的沉降数据样本值用Gompertz模型、Logistic模型、灰色Verhulst模型3种模型进行拟合求解并预测后4期沉降值，各模型的沉降预测曲线如图1所示。各预测模型精度指标值的比较如表3所示。

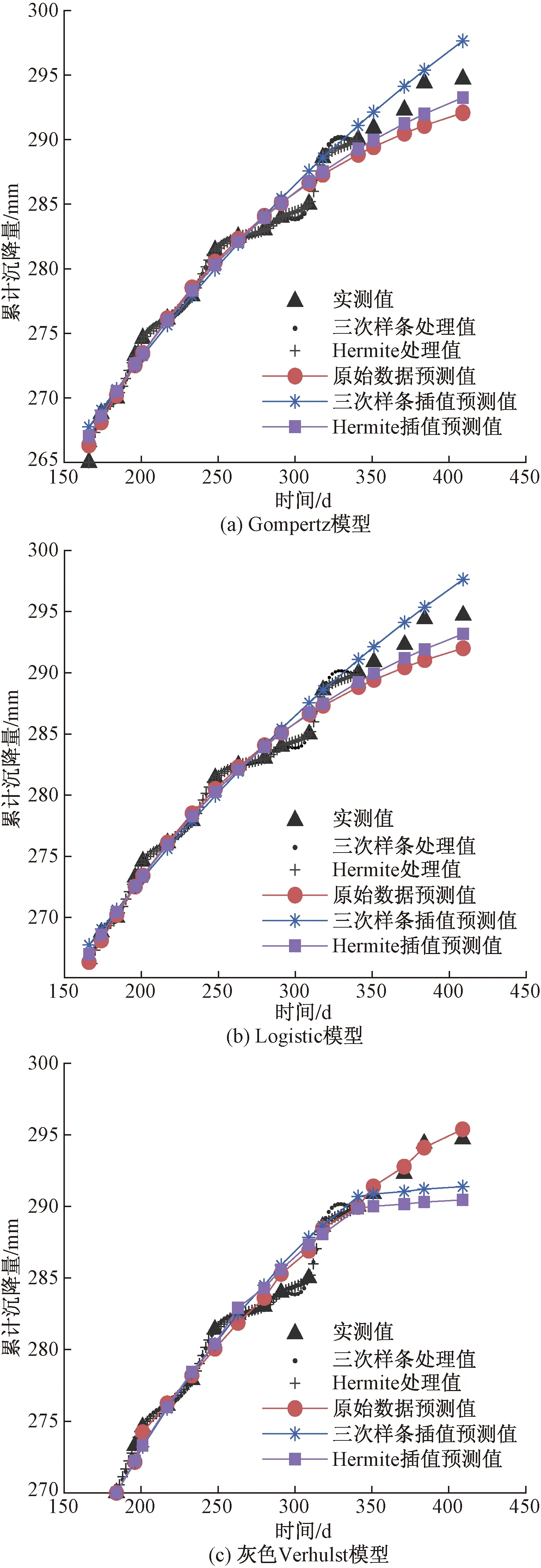
图1 常张高速各模型等时距处理方法对比Fig.1 Comparison of equal-interval processing methods for different models of Chang-Zhang highway

表3 常张高速各预测模型精度评价指标的比较Table 3 Comparison of precision evaluation indexes of different prediction models for Chang-Zhang highway

由表3可知，3种模型的3种情况的拟合优度均大于95%，置信水平显著；MAPE均小于10%，属于高精度预测。其中Gompertz模型和Logistic模型基于分段三次Hermite插值后的样本值的拟合程度和预测精度都更高于其他两种情况。灰色Verhulst模型3种情况的小误差概率均为1，后验差比值均小于0.35，预估模型精度等级为“好”，根据拟合优度和SSE、MAPE、MSE、MAE预测评价指标，以原始沉降数据作为样本值灰色Verhulst模型的预测精度更高。

由图1(a)、图1(b)可知，在沉降速率明显下降的时候，如291～309 d和318～341 d时间段，三次样条插值虽然有连续曲率(二阶导数连续)具有足够的光滑性，但是明显比三次分段Hermite插值更偏离原始沉降数据。对于Gompertz和Logistic两种模型，以分段三次Hermite插值处理的数据作为样本值的拟合效果和预测效果更优。

3.2 内蒙古乌-噶一级公路软土路基

内蒙古沙漠地区乌审召生态工业园区——噶鲁图段一级公路(简称乌-噶一级公路)在K35+100～K35+800之间为软土路基[12]，地勘资料表明在该路段地势低洼，表层0.2 m范围内为细砂，0.2 m以下为3.5～5.4 m厚的粉土及淤泥质粉土夹层，地下水位较高为0.6 m，透水性不好，力学指标较差，地基承载力低。该路段主要采用了置换、挤密等综合方法对土体改良加固，对加固后的软土路基进行动态监测。

为提高模型预测精度，通过对样本值比选，适当剔除观测前期数据，以201 d前的观测数据为各个预测模型的样本值，对234～328 d共94 d的4期数据进行预测。其中Gompertz模型和Logistic模型以29～201 d的观测值作为样本值，灰色Verhulst模型以76～201 d的观测值作为样本值。

根据第2节中所述的分段三次Hermite插值和三次样条插值求解方法，分别对3种单一预测模型进行处理得到等时距的沉降数据样本值。对原始观测沉降值以及两种等间距处理的沉降数据样本值用Gompertz模型、Logistic模型、灰色Verhulst模型3种模型进行拟合求解并预测后4期沉降值，沉降预测曲线如图2所示。各个预测模型精度指标值的比较如表4所示。

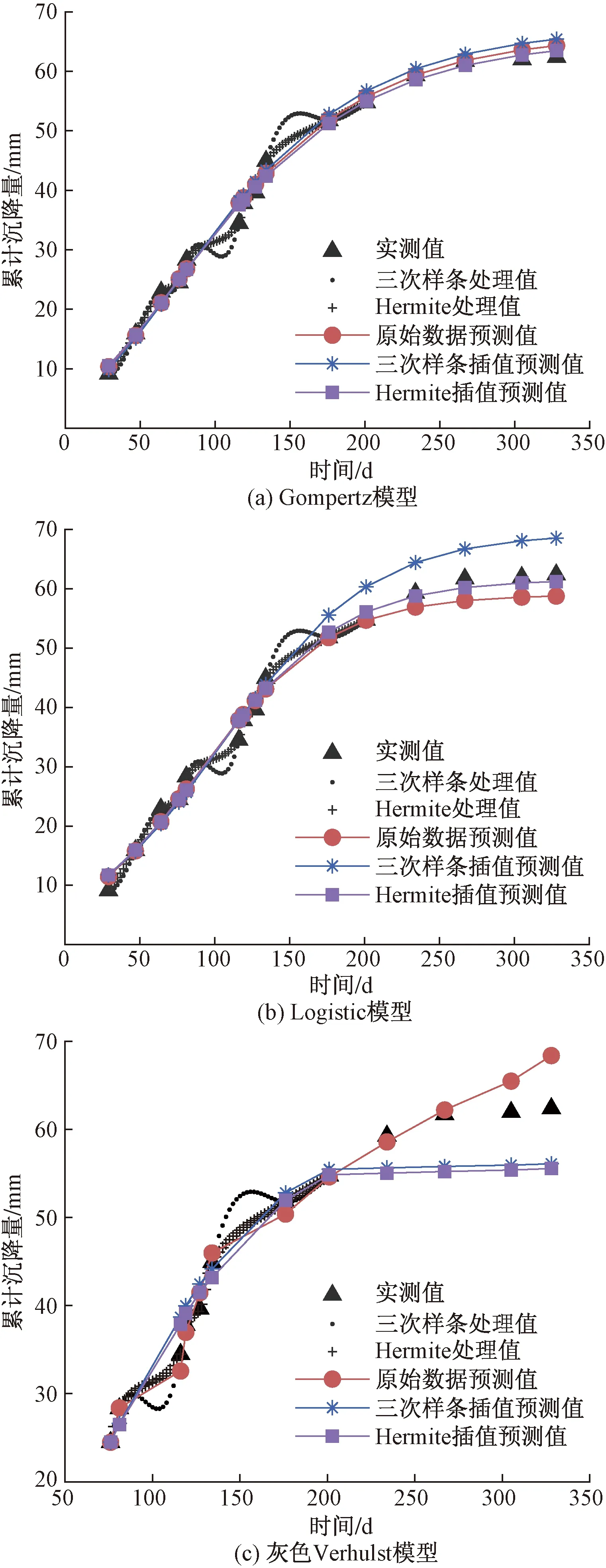
图2 乌-噶一级公路各模型等时距处理方法对比Fig.2 Comparison of equal-interval processing methods for different models of Wu-Ga first class highway

由表4可知，除灰色模型情况2外，3种模型的3种情况的拟合优度均大于95%，置信水平显著；MAPE均小于10%，属于高精度预测。Gompertz模型和Logistic模型以分段三次Hermite插值后的数据为样本值的拟合程度和预测精度都更高于其他两种情况。灰色Verhulst模型3种情况的小误差概率均为1，后验差比值均小于0.35，预估模型精度等级为“好”。根据拟合优度和预测评价指标，原始沉降数据为样本值时，灰色Verhulst模型的预测精度更高。

由图2(a)、图2(b)可知，91 ～116 d和134 ～176 d时间段沉降速率明显下降，经三次样条插值处理的数据比三次分段Hermite插值处理的数据更偏离原始沉降数据。乌-噶一级公路用Gompertz和Logistic两种模型预测时，以三次分段Hermite插值处理的数据为样本值的拟合效果和预测效果更优。

结合常张高速公路和乌-噶一级公路两工程实例分析，在用Gompertz和Logistic两种模型以沉降速率发生明显变化时刻的数据作为最后一组样本值进行预测时，推荐选用分段三次Hermite插值对原始沉降数据进行等时距处理后再预测沉降量。对于灰色Verhulst模型，推荐采用原始沉降数据为样本值进行沉降预测。

4 组合预测模型对比分析

4.1 常张高速公路软土路基

第3节中计算结果表明，常张高速公路Gompertz和Logistic模型经分段三次Hermite插值的沉降数据为样本值时预测精度更高，因此在组合预测中将两种模型的情况3作为单预测模型。灰色Verhulst模型以原始沉降数据为样本值预测精度更高，因此在组合预测中将灰色模型的情况1作为单预测模型。

基于建立的3种单模型，将其每时刻的预测值按照精度高低进行排序，分别运用MATLAB的非线性优化工具箱和遗传算法(genetic algorithm，GA)两种方法求解基于IOWHA算子的组合模型的最优权系数，并将这两种方法的组合预测结果及单项预测模型的精度进行对比分析。由GA得到组合模型1的最优权系数为l1=0.832,l2=0.010,l3=0.158。由MATLAB非线性优化工具箱计算得到的组合模型2的最优权系数为l1=0.424,l2=0.288,l3=0.288。

各单项模型及组合模型的预测结果及评价指标值分别如表5、表6所示。各单项模型、组合模型的预测曲线与实测值的对比结果如图3所示。

由表5、表6、表1可知， 5种模型均属于高精度预测。组合模型1的MAPE分别比Gompertz模型、Logistic模型、灰色Verhulst模型和组合模型2降低75%、76%、26%和49%。由图3可见，在后4期的预测结果中组合模型2的曲线更接近实际沉降量。所以GA求解基于IOWHA算子的组合模型的最优权系数的方法能够提高模型的精度。

4.2 内蒙古乌-噶一级公路软土路基

第3节的计算结果表明，乌-噶一级公路Gompertz模型和Logistic模型经过分段三次Hermite插值的沉降数据为样本值预测精度更高，灰色Verhulst模型以原始沉降数据为样本值预测精度更高。因此在组合预测中将因此在组合预测中将Gompertz模型和Logistic模型两种模型的情况3和灰色模型的情况1作为单一预测模型。

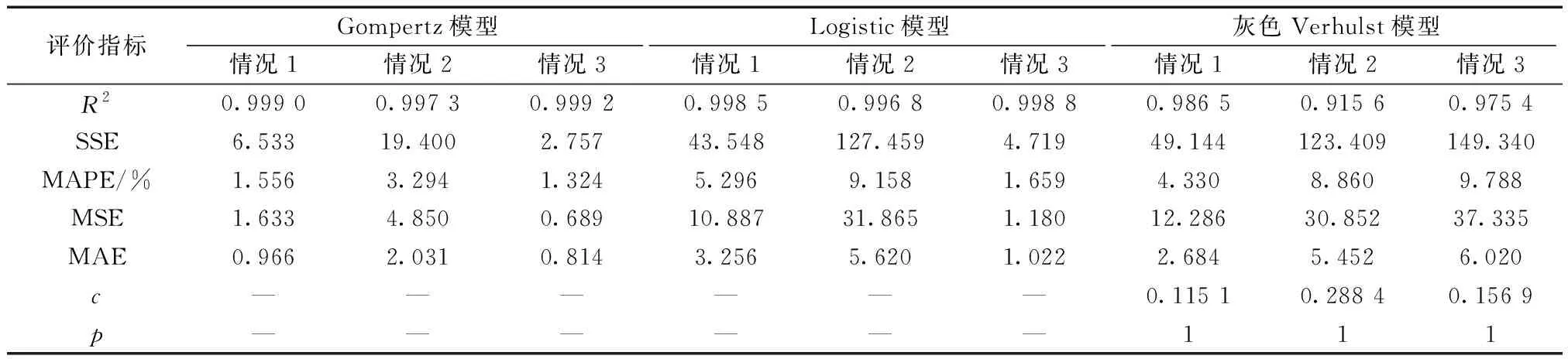
表4 乌噶一级公路各预测模型精度评价指标的比较Table 4 Comparison of precision evaluation indexes of different prediction models for Wu-Ga first class highway

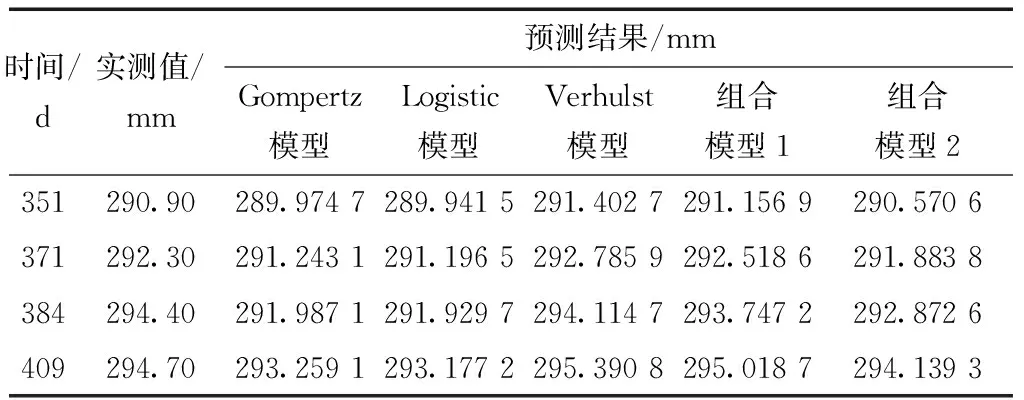
表5 常张高速公路各模型预测结果Table 5 Prediction results of various models of Chang-Zhang highway

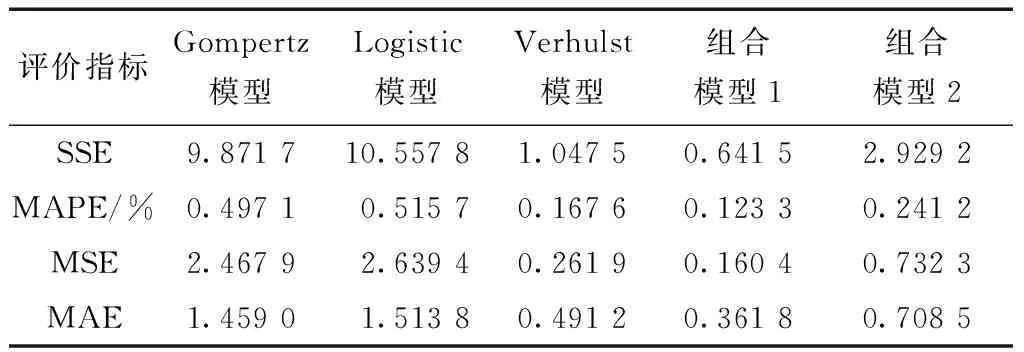
表6 常张高速公路各预测模型精度评价指标的比较Table 6 Comparison of precision evaluation indexes of different prediction models for Chang-Zhang highway

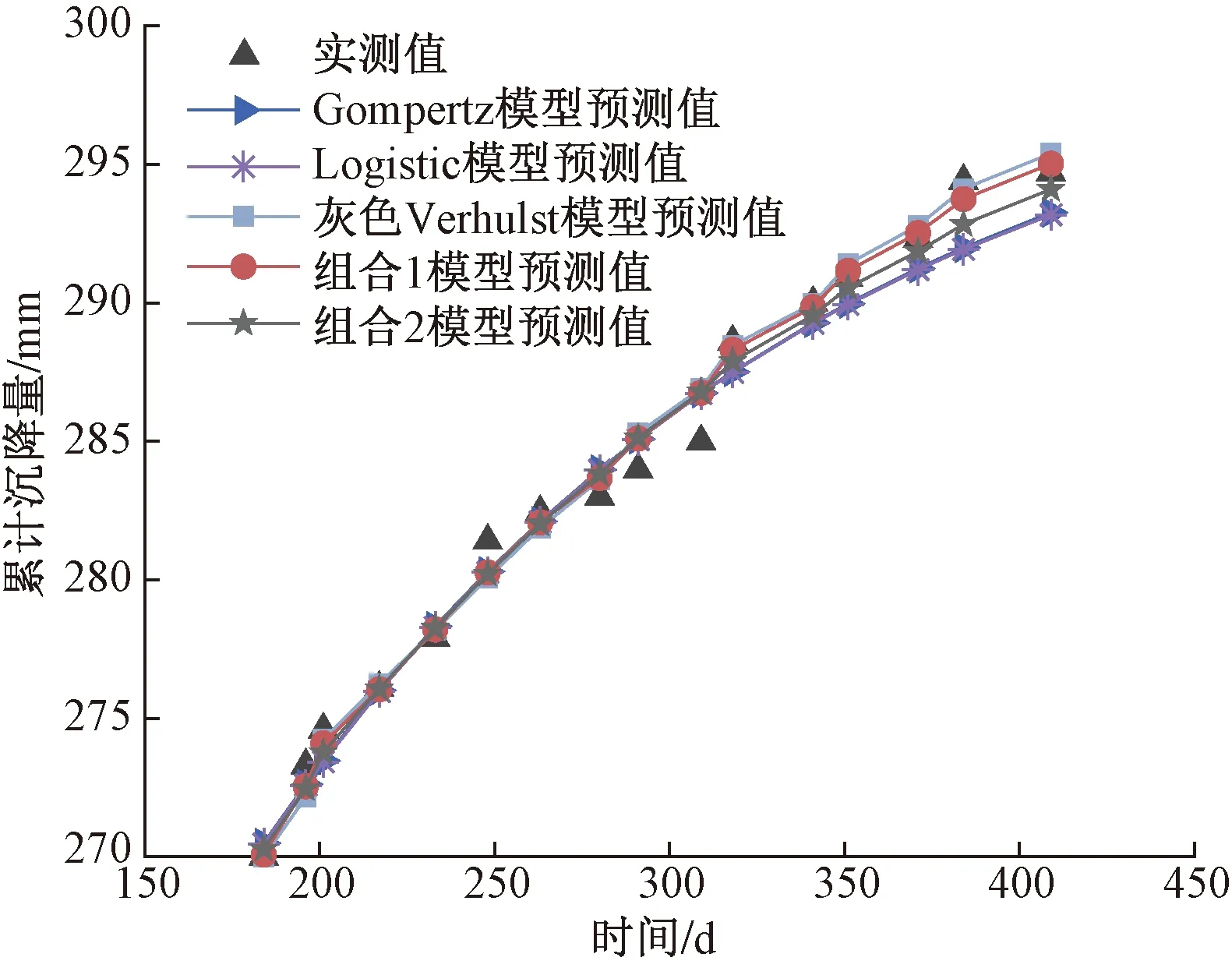
图3 常张高速公路沉降预测曲线Fig.3 Settlement prediction curve of Chang-Zhang highway

基于建立的3种单模型，分别运用MATLAB的非线性优化工具箱GA两种方法求解基于IOWHA算子的组合模型的最优权系数，并将这两种方法的组合预测结果及单项预测模型的精度进行对比分析。由GA得到组合模型1的最优权系数为l1=0.553,l2=0.447,l3=0.000。由MATLAB非线性优化工具箱计算得到的组合模型2的最优权系数为l1=0.501,l2=0.251,l3=0.248。

各单项模型及组合模型的预测结果及评价指标值分别如表7、表8所示。各单项模型、组合模型的预测曲线与实测值的对比结果如图4所示。

表7 乌-噶一级公路各模型预测结果Table 7 Prediction results of various models of Wu-Ga highway

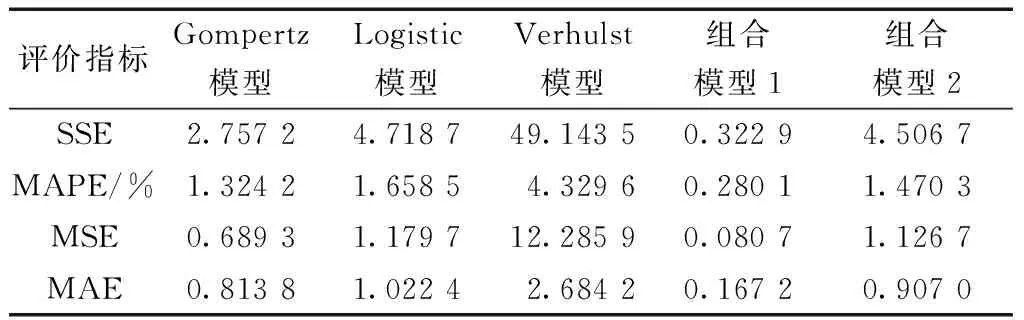
表8 乌-噶一级公路各预测模型精度评价指标的比较Table 8 Comparison of precision evaluation indexes of different prediction models for Wu-Ga highway

图4 乌-噶一级公路沉降预测曲线Fig.4 Settlement prediction curve of Wu-Ga highway

由表8可知，组合模型2 的平均绝对百分比误差分别比Gompertz模型、Logistic模型、灰色Verhulst模型和组合模型2降低79%、83%、93%和81%。由图3可知，灰色Verhulst模型后四期的预测结果大于沉降实测值，而Gompertz模型和Logistic模型后4期的预测结果小于沉降实测值，所以采用Gompertz模型、Logistic模型和灰色Verhulst模型进行组合预测是合理的。同时，在后4期的预测结果中显然组合模型2的曲线更接近实际沉降量且该模型的曲线更加平稳。

5 结论

通过分析常张高速公路K159+585断面和乌噶一级公路K35+270断面处软土路基的实测沉降数据和预测模型，得出以下主要结论。

(1) 路基沉降是一个复杂非线性的过程，固结沉降的发展过程符合“S”形曲线的变化规律。同时通过两个工程实例表明，Gompertz模型、Logistic模型和灰色Verhulst模型能够较好拟合软土路基中短期沉降，Gompertz模型、Logistic模型的预测值比实测值偏小，而灰色Verhulst模型预测值比实测值总体偏大，所以进一步验证用这3种类模型作为单一模型进行组合预测来描述软土路基的沉降是合理的。

(2)通过用Gompertz模型、Logistic模型和灰色Verhulst模型分别以原始沉降数据、经三次样条插值处理的数据、经分段三次样条插值处理的数据作为样本值进行预测。结果表明，在沉降速率发生明显变化时刻的数据作为最后一组样本值进行预测时，Gompertz和Logistic模型选用分段三次Hermite插值对原始沉降数据进行等时距处理后预测的预测效果更好。灰色Verhulst模型将原始沉降数据作为样本值进行沉降预测的预测结果精度更高。

(3)基于IOWHA算子的组合预测模型包括Gompertz模型、Logistic模型和灰色Verhulst模型3种模型，能够充分发挥3个单一模型的优势，考虑了每时刻单一模型的预测精度克服传统加权调和平均组合预测方法的缺陷，有效降低单项预测模型预测结果的误差，提高了模型的预测精度。

(4) 对于组合模型加权系数的求解MATLAB的非线性优化的工具箱求解的结果与给定的初始值有关，采用GA较使用MATLAB的非线性优化的工具箱求解组合模型的加权系数更为可靠，得到的组合模型的预测精度更高。