冬冷干燥地区整体建筑热湿耦合传递对室内温湿度的影响

郑伟花， 宋朝

(河北大学建筑工程学院， 保定 071002)

围护结构是建筑物的重要组成部分，同时也是建筑物热湿负荷的主要来源[1]。从理论上，其内部的热湿耦合传递可以抽象为多孔介质内热湿耦合迁移过程。众多学者根据不同的机理进行了相应的研究，并取得了很多成果。戚禹康等[2]研究了稻谷自然储存多尺度热湿耦合传递；于水[3]分析了热湿耦合作用建筑墙体的相关问题；Melin等[4-5]、Lu[6]建立了多孔介质材料的热湿耦合传递模型；郭兴国等[7]研究了夏热冬冷地区太阳辐射对墙体内部热湿耦合迁移的影响；刘向伟[8]分析了夏热冬冷地区建筑墙体热、空气、湿耦合迁移特性；黄祖坚等[9]通过对北美典型气候区建筑围护结构热量和湿分耦合传递模型(coupled heat and moisture transfer model，HM)模拟及分析，建立了多孔介质材料的热湿耦合传递模型。

目前，关于冬冷干燥地区多层墙体的研究鲜见报道。实际上，在相同温度下由于湿度的差异，建筑外墙的保温隔热大相径庭。为此，针对目前市场上常见的复合墙体结构和墙体材料的整体性能进行研究，创建适合用于北方冬季寒冷干燥地区的复合墙体体系。以超低能耗建筑的一楼为研究对象,分别对不同外墙保温下建筑在冬季寒冷干燥地区的热湿传递情况进行模拟，分析不同外墙保温系统下整体建筑热湿传递特性的差异。为冬冷干燥地区的多层墙体构建提供科学依据。

1 数学模型

以温度和相对湿度为驱动势，根据能量守恒和质量守恒定律建立墙体热湿耦合传递瞬态模型，并做以下假设：①建筑材料是在维数上恒定不变的多孔材料，且多孔介质内的流体是连续性的、均匀分布的理想气体；②墙体内部介质连续且各向同性，局部热力学平衡；③建筑材料内部介质的部分物性参数为恒定不变的常数；④空气压力恒定为大气压；⑤忽略液态水弥散过程；⑥忽略结冰现象；⑦建筑材料之间处于湿平衡状态。参考文献[10]建立该建筑的热湿平衡方程。

1.1 湿传递

所研究的湿传递认为湿度变量是包含水蒸气和液态水的总量，涉及毛细管吸力下的液态水传递和水蒸气的扩散传递，因此以Dancy定律和菲克扩散定律为基础,考虑到建筑材料一般被恒定的大气压力环境包围，并在一定范围的温度和水分条件下，建立了此类材料的水分运输方程，由假设①可知，应使用毛细孔内的流体扩散模型

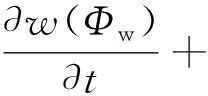
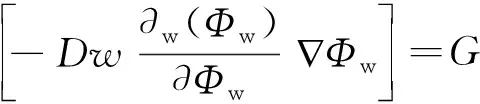
(1)

式(1)中：∇为梯度；ρgug∇ωv为时控器所导致的水分变化率。

根据假设④，绝对压力PA设置的为1.013 25×105Pa,这时候流体间的对流通量会消失，因此

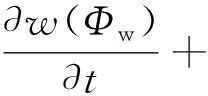
(2)

通过引入水分储湿量，可得

(3)

蒸汽的扩散通量可表示为

gw=-pgDeff∇ωv

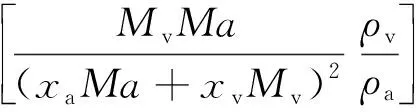
(4)

通过令xaMa+xvMv为常数，且潮湿的空气为理想的气体，因此有

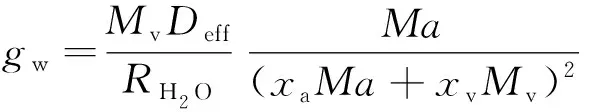
(5)

蒸汽渗透系数为

(6)

最后可得

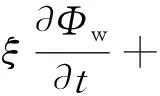
(7)

式中：w为材料体积含湿量，kg/m3；Φw为相对湿度；pg为潮湿空气密度，kg/m3；ug为单位横截面积的体积流速，m/s；ωv为潮湿空气中的水蒸气质量分数；gw为水分扩散通量；u1为液态水的流速，m/s；ρ1为液态水的密度，kg/m3；Dw为水分扩散性,m2/s；G为水分来源,kg/(m3·s)；Deff为多孔介质中的有效蒸汽扩散系数，m2/s；Mv为水蒸气的摩尔质量，kg/mol；Ma为多孔介质内流体的马赫数；xa为干燥空气的摩尔分数；xv为水蒸气的摩尔分数；ρv为水蒸气分压，Pa；ρa为干燥空气的压力，Pa；RH2O为水蒸气气体常数，J/(kg·K)；ξ为水分存储量，kg/m3；δP为蒸汽渗透性，s；Psat为饱和水蒸气压力，Pa；T为温度，K。

1.2 热传递

研究建筑在自然条件形成的对流换热[11]，属于宏观热对流，微观热传导。因此热传递只考虑热传导和热对流。热量在建筑材料内部处于活动状态，因此采用非稳态的模型，将材料定义为含有液态水和蒸汽的多孔介质。根据假设①和假设②可知建筑材料是连续的、局部热力学平衡的多孔介质而且其内部的流体具有连续性，因此热传递方程应根据能量守恒定律和热力学第一定律建立，方程的建立要考虑建筑材料的属性和材料内的水分。局部热平衡方程为

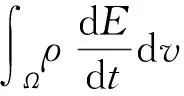
(8)

以时间为变量，建筑的能量的变化主要是由内部能量的对流、热传导、辐射、机械应力的消散和额外的体积热源来平衡的。因此考虑空间框架的热力学平衡方程为

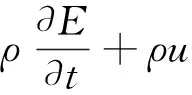
(9)

由于选择的干燥材料具有导热性，因此可以忽略由湿空气所引起的部分体积变化，有效导热系数可以被定义为关于固体和水分特性的函数，可表示为

(10)

式中：Ω为多孔介质内的均质流体；E为质量内能，J/kg；v为多孔介质的体积，m3；q为通过传导产生的热量，J；n为边界∂Ω的外部法向量；s熵，J；σ为柯西应力张量；ρ为固体的干密度;(ρCp)eff为恒定压力下的有效体积热容量,J/(m3·K)；q为传导传热通量项；Q为总热量，W/m3；keff为有效导热系数,W/(m·K)；t为时间，s；qr为辐射热通量，W/m2；ks为干固体热导率，W/(m·K)；b为热导率补充，无量纲；ρs为固体的干密度，kg/m3。

热容量为描述在干燥的固体材料中，单位质量产生单位温度变化所需的热能量。定义恒定压力下的有效体积热容量，需要同时考虑固体矩阵的特性和湿度。

(ρCp)eff=ρsCp,s+w(Φw)Cp,w

(11)

式(11)中：Cp为恒定应力下的比热容，J/(kg·K)；(ρCp)eff为恒定压力下的有效体积热容，J/(m3·K)；w(Φw)为着水分存储功能，用来描述储水量与材料中相对湿度之间的关系；Cp,s为固体干燥时的热容量;Cp,w为水热容量在恒定的压力。

汽阻因子μ将蒸汽渗透性定义为δp，由此可得

(12)

式(12)中：δ为静止空气的蒸汽渗透性，s。

根据假设①，由于建筑材料为含有液态水和蒸汽混合物的多孔介质，所以将由于水分转移引起的材料性质的总体变化通过表观导热系数的变化以及热源来表示，并且考虑蒸发潜热后可得

(13)

式(13)中：Lvδp∇(ΦPsat)为由于水分含量变化而产生的热源;Lv为潜热,J/kg;Psat为饱和水蒸气压力，Pa。

1.3 边界条件

考虑水分蒸发所导致的潜在热源[12]，湿气通量为墙体增加水分。选择压力差所导致的对流水汽通量，通过墙体的湿流量g0可表示为

g0=βρ[Φw，extρsat(Text)-ΦwPsat(T)]g0=βρ

(14)

式(14)中：βρ为水分转移系数；Φw,ext为外部相对湿度；Text为外界环境温度，℃；g0为进入墙体材料的湿气通量，g0>0。

-ngw=0

(15)

式(15)意味着边界上没有水汽通量。跨越边界的相对湿度梯度为零。与此同时，边界一侧的相对湿度必须等于另一侧的相对湿度。由于边界之间没有相对湿度差异，湿气无法穿过边界[13]。所以式(15)只能应用于外部边界。添加跨边界的热通量，使得为域增加热量的热通量为正。由于本研究中所采用的是外界环境中的自然通风形成的对流换热，因此为自然对流换热[2]。

通过墙体的热通量q0可表示为

q0=h(Text-T0)

(16)

式(16)中：h为传热系数；T0为初始值，℃。

-nq=0

(17)

此时意味着边界之间没有热通量。通过这个方程，可以了解到跨越边界的温度梯度是零。要达到这个结果，边界一侧的温度必须等于另一侧的温度。由于边界之间没有温差，所以热量无法穿过边界。

水平平板上侧的外部自然对流传热系数h的取值为

(18)

垂直壁的外部自然对流传热系数的取值为

(19)

式中:k为导热系数，W/(m·K)；ReL为与特征长度L相关的雷诺数；cp为恒定压力下的特定热容量，J/(kg·K)；L为特征长度(面积/周长)，m。

2 模拟条件

图1为以河北省保定市某被动式超低能耗示范工程为研究对象建立的物理模型，模型按照实建筑原尺寸构建，其中为了简化问题，选取建筑的一楼作为数值模拟的对象，实建筑内部横跨21.4 m，内宽12.35 m，室内高度为3.75 m。该建筑从室外到室内，依次由防护层、保温层和基层墙体组成。各层材料厚度尺寸为：防护层采用60 mm混凝土保护层，保温层为280 mm厚的石墨聚苯板，南边的基层墙体采用200 mm厚钢筋混凝土墙，其余部分的基层墙体则为300 mm厚的钢筋混凝土墙。如图2所示，为了得到建筑内部某个位置的温度和湿度数据，在模拟过程中设置了3个监测点来记录建筑内部的温湿度变化[14-15]。3个监测点的位置分别为监测点1(0.6、0.7、0.6 m)、监测点2(11.24、6.765、2.05 m)、监测点3(21.88、12.93、1.925 m)，其中监测点1和监测点3靠近墙壁，监测点1在该建筑的左侧(南墙壁)左下角，监测点3在该建筑的右侧(北墙壁)右上角。因为四周的墙壁直接与大气接触，所以靠近墙壁的位置容易受大气环境的影响[16-18]，故在两侧的墙壁附近各设置一个监测点，而建筑内部受大气环境的影响不是很大，因此在建筑中部设置一个监测点。模拟所用建筑材料参数均根据《实用供热空调设计手册》[11]和模拟软件自带的建筑材料库确定，建筑墙体各层材料参数如表3所示。

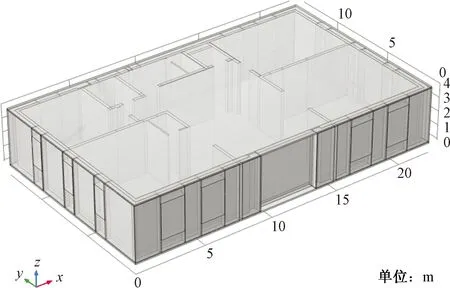
图1 建筑物理模型Fig.1 Building physical model

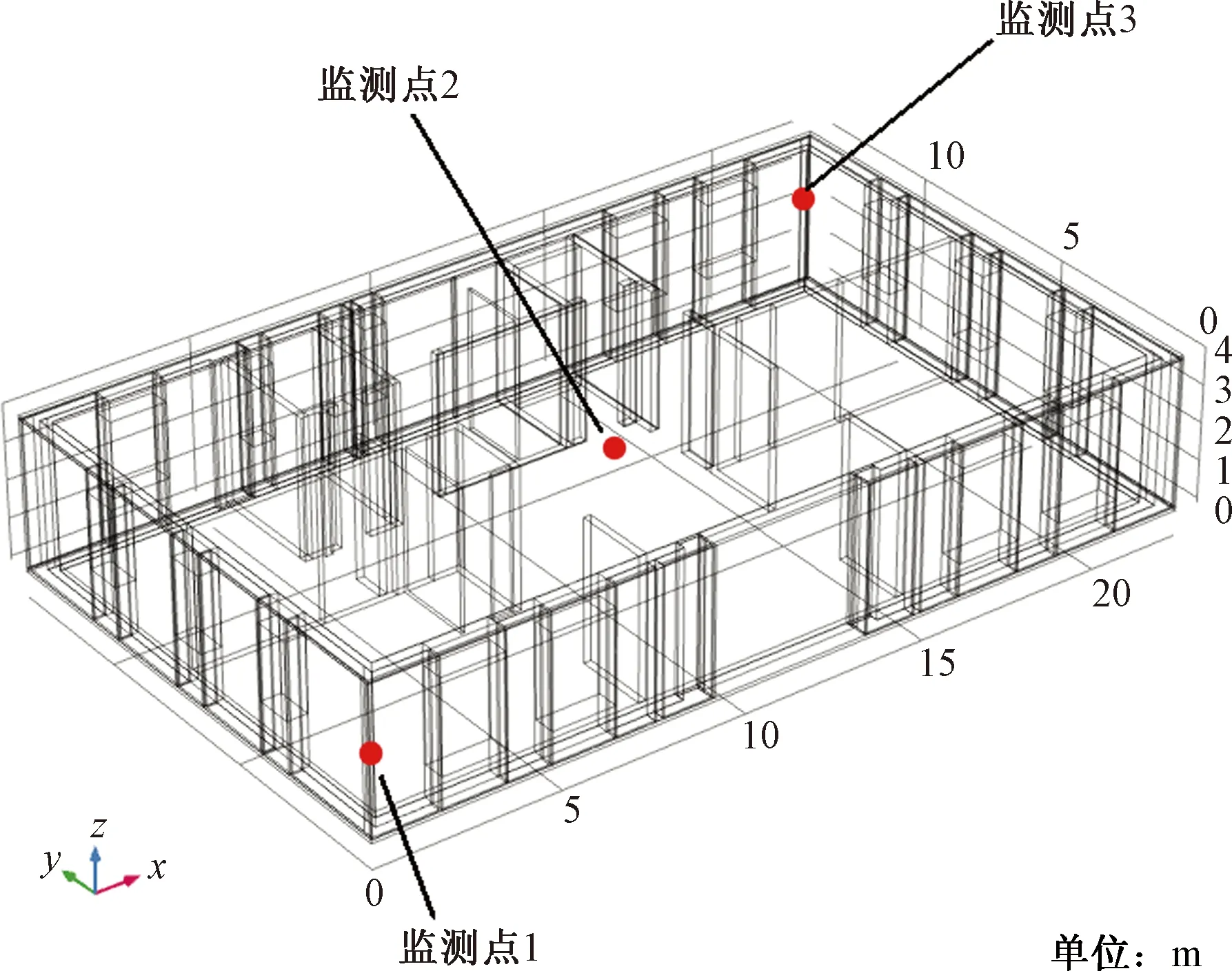
图2 监测点位置Fig.2 Location of monitoring points

3 墙体热湿耦合传递模型的求解

3.1 热湿耦合传递模型求解

选择保定作为研究的模拟城市，气象数据(ASHRAE 2017)逐时值作为气象参数。为了使模拟结果更加准确，保定地区选用供暖情况下的状态(室内温度为20 ℃)，室内相对湿度设为0.3，建筑朝向设置为坐北朝南。模拟开始时间为2017年12月30日0：00，持续时间24 h,建筑围护结构初始温度设置为当日的环境温度，设定保温层初始相对湿度为当日的环境湿度。在材料参数的设置中，可以根据参考温度对密度进行评估，以确保在温度变化时保持所需要的质量。采用Tempref算法，将温度设置为293.15 K。模型求解后的温度、相对湿度分布分别如图4、图5所示。

图6为封闭情况下3个监测点记录的温度变化情况，它们的温度变化情况具有规律性。监测点1与监测点3呈对称状态，对称点为监测点2。从图6(a)中可以看出，在测量初期，监测点2的温度最高，这是因为该点测量的是室内空气温度(室内温度设为供暖状态下的20 ℃)，之后随着温度的降低，由于温度的延滞效应，在封闭阶段监测点2的温度逐渐降低。监测点1和监测点3在最初封闭时，温度变化出现先陡后缓的情况，这是因为在封闭初期该点的温度为靠近墙体的室内空气温度，所以刚开始墙壁的温度(环境温度)随着空气传递到了该处导致温度出现骤降，并逐渐与环境温度持平。监测点1和监测点3温度接近外界大气温度，这是由于这两点距离墙体较近，而建筑墙体受外界大气温度影响比较大。从图4可以清楚的看出，封闭期间室内温度分布非常均匀，空气区域为自然对流运动，均匀的气流为室内温度快速降温降湿提供了条件。由于南边的玻璃厚度与钢筋混凝土的厚度均高于其它方向，因此监测点1的温度下降速度比监测点3的温度下降速度要慢，24 h后室内的平均温度分别为3.75 ℃。

表3 相关材料参数Table 3 Relevant material parameters

图4 7.5 h后温度分布Fig.4 Temperature distribution after 7.5 h

图5 7.5 h后相对湿度分布Fig.5 Relative humidity distribution after 7.5 h

图6 不同室内温度下24 h内的温度变化Fig.6 Temperature change within 24 hours under different indoor temperature

图4为封闭7.5 h后的建筑温度分布。随着时间的推移，温度相对于封闭初期产生了些许变化。室内正中间位置的温度初期变化不明显，保持在20 ℃。室内的低温出现在墙壁处，这与外界环境有关，平均温度下降了11 ℃。由于保温层采用的石墨聚苯板，该材料吸水率偏高，容易吸水。而建筑墙体位于外界寒冷和室内常温两个温度交叉点，极易产生水分，而室内温度较高, 水分蒸发带走大量热量，从而导致低温在此。同时，室内温度分布比较均匀，这是因为石墨聚苯板的绝热能力超强，它含有特殊的石墨颗粒，可以像镜子一般反射热辐射，并且其中含有能够大幅度提升保温隔热性能的红外线吸收物，从而减少房屋的热损失。

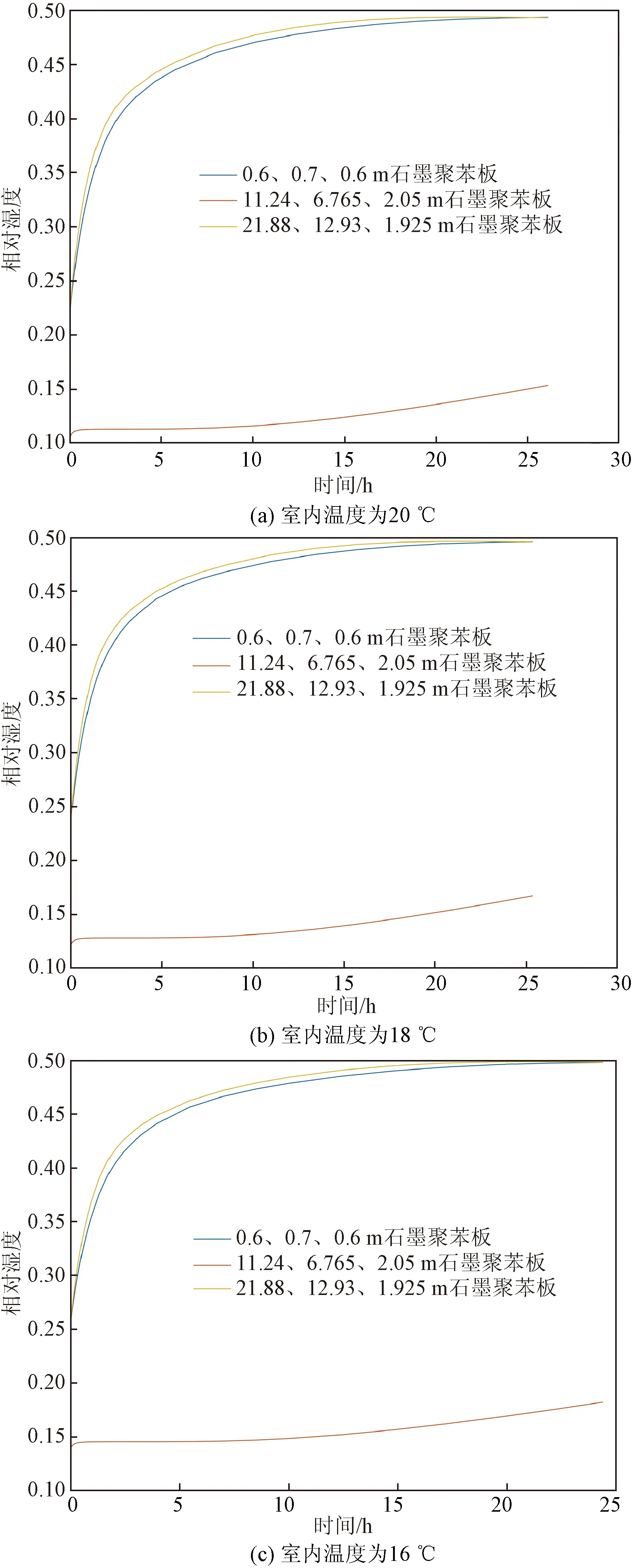
图7 不同室内温度下24 h内的相对湿度变化Fig.7 Change of relative humidity within 24 hours under different indoor temperature

从图7可以看出，监测点的水分变化有急有缓，但是总体是上升的趋势，这是因为建筑内部是一个封闭的小空间。冬季室内外温差大,容易产生冷凝水，图5为7.5 h后建筑内部的水分分布，经过7.5 h后，建筑墙体处的相对湿度升高大约28%，随着时间的流逝，24 h后室内的平均相对湿度为0.38。

3.2 采用EPS保温层的影响

聚苯乙烯泡沫(EPS)保温板是中国应用广泛的一种保温材料。为了比较在冬冷干燥地区使用EPS板与石墨聚苯板后室内温湿度的差异，对其使用过程中的热湿传递进行模拟。将外围护结构的石墨聚苯板保温层换成EPS保温板后，监测点2的含湿量分布和变化规律与采用石墨聚苯板时相同。从图8中可以看出，与使用石墨聚苯板时相比，靠近墙体处的相对湿度增加，远离墙体处的相对湿度降低。这是因为EPS保温板导热系数小，蓄热系数大。它能够减少室外湿分向墙体内的渗透，同时还削弱了室内湿分向外界的扩散。EPS保温板不吸水，因此，其保温层的水分低于石墨聚苯板保温层，所以靠近墙体处的相对湿度低于装备石墨聚苯板时的相对湿度。水分减少，蒸发吸收的热量减少，也因此，从图8(a)中可以得到靠近墙壁处的温度比石墨聚苯板时的温度高。并且经过24 h的封闭模拟，室内的平均温度为4.20 ℃。从图8(b)可以看出，当外围护结构中的含湿量趋于稳定后，域点探针3的相对湿度要低于域点探针1的相对湿度，24 h后室内的平均相对湿度为0.365。这是因为EPS板的隔水性能良好，其保温层的水分要低于石墨聚苯板作为保温层时的水分，保温层散发热量导致顶部水分率先蒸发，所以相对湿度较低。水分蒸发，水蒸气向上运动，也因此它的温度较高。

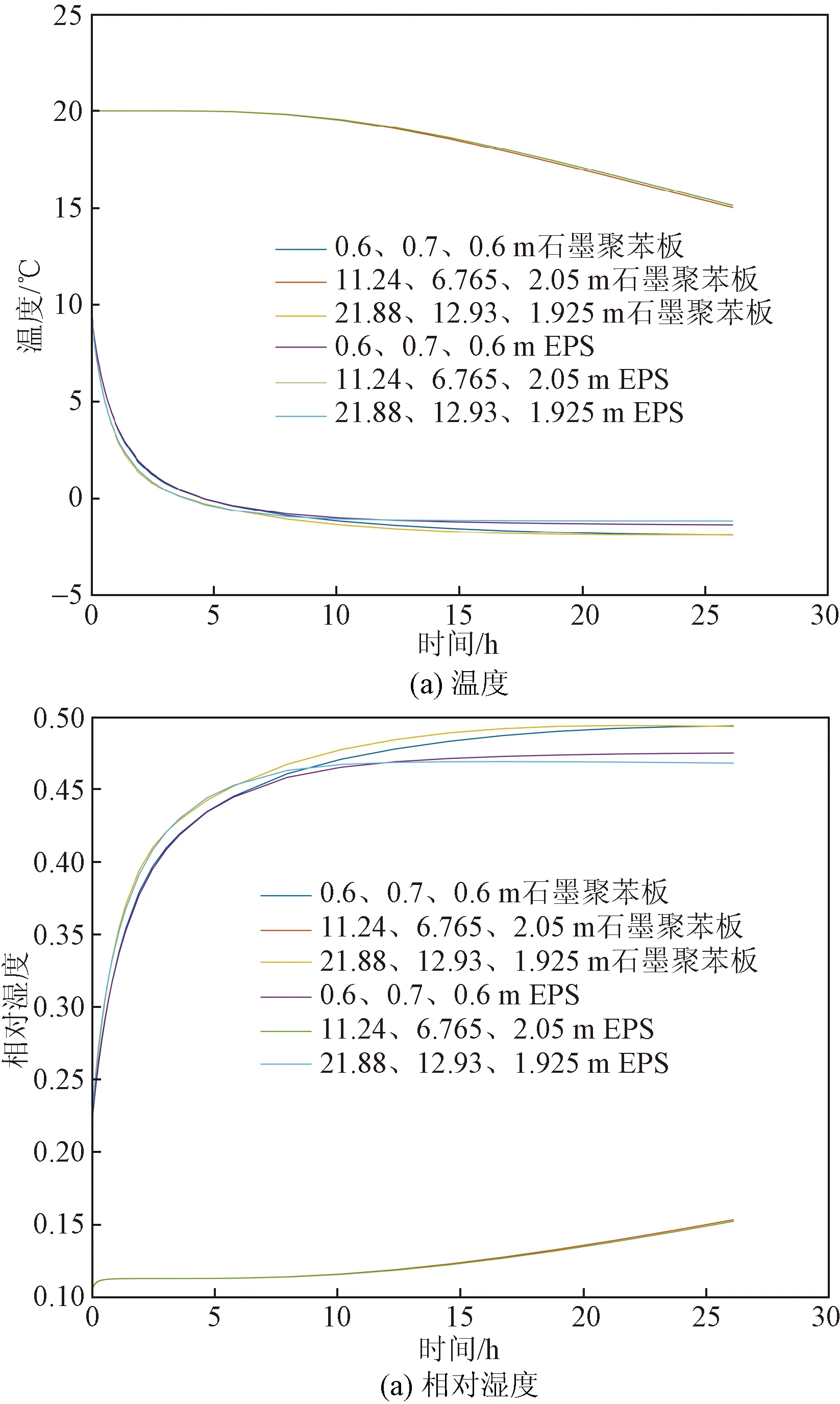
图8 20 ℃时两种材料对比Fig.8 Comparison of two materials at 20 ℃

3.3 室内温度对热湿分布的影响规律

在冬冷干燥地区，人们为了满足居住的舒适性，通常会使用采暖设备使房间温度升高。由以上内容可知，建筑的东北角顶部(探针3)相对湿度较高，为准确反映室内温度对该位置的相对湿度分布的影响，基于数值模拟所得到的温度和相对湿度数据, 通过exponential函数进行拟合。依据查阅相关知识可得，室内温度为18 ℃时为人体最舒适温度。因此将室内温度设置为18 ℃，相对湿度0.3进行为期24 h的模拟，探求室内温度对热湿分布的影响规律。

靠近东北角屋顶室中央温度和墙壁处温度的数据拟合公式为

f(x)=-3.172×10-6exp(-7.14x)+17.98

(20)

根据式(20)中系数(95%置信区间)，拟合结果的评价参数分别为：误差平方和1.301、线性回归拟合确定系数0.968、调整后回归拟合确定系数0.966 1、标准差0.201 6。根据这些参数可知，曲线拟合度较好，能够反映东北角屋顶墙壁处温度和室中央温度之间的变化过程，数据拟合曲线如图9所示。

图9 靠近东北角屋顶墙壁的温度和室中央温度 的数据拟合曲线Fig.9 Data fitting curve of the temperature of the roof wall near the northeast corner and the temperature in the center of the room

靠近东北角屋顶墙壁处温度和其相对湿度的数据拟合公式为

f(x)=57.49x2-83.05x+25.14

(21)

根据式(21)中系数(95%置信区间)，拟合结果的评价参数分别为：误差平方和0.031 09、线性回归拟合确定系数1、调整后回归拟合确定系数0.999 9、标准差0.031 17。根据这些参数可知，曲线拟合度较好，能够反映东北角屋顶墙壁处相对湿度和其温度之间的变化过程，数据拟合曲线如图10所示。

将式(20)、式(21)联立可得墙壁相对湿度和室内温度的数据拟合方程为

f(x)=-3.172×10-6exp[-7.14(57.49x2-83.05x+25.14)]+17.98

(22)

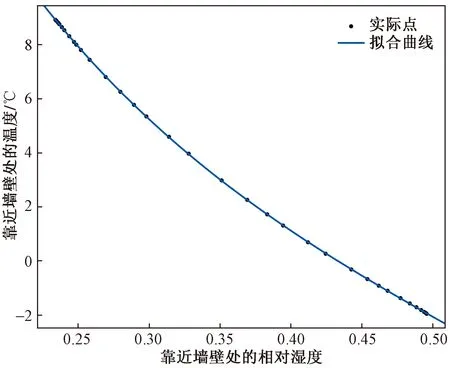
图10 靠近东北角屋顶墙壁的相对湿度和其温度 的数据拟合曲线Fig.10 Data fitting curve of relative humidity and temperature of roof wall near the northeast corner

4 结论

采用有限元法对保定市某被动式超低能耗示范工程整体建筑的室内温度和水分变化规律进行了数值模拟，对模拟结果进行了分析研究，得出以下结论。

(1)在冬冷干燥地区相同温湿度条件下，两种保温材料的性能存在差异。在吸湿能力这方面，EPS板小于石墨聚苯板；但是在保温能力方面，EPS板大于石墨聚苯板。

(2)保温外墙处于室内外温差交界处，容易产生冷凝水。室内温度较高时，随着保温外墙的水分吸热蒸发，靠近墙体的周边温度逐渐降低。因此整体建筑处于封闭阶段时，室内最低温度出现在墙壁附近。

(3)水分蒸发带走大量热量，热量在室内中心位置与边缘位置的传递存在延迟效应，封闭阶段靠近墙壁的空气率先降温，随后逐渐延伸到室内中央位置，因此，靠近墙壁处的相对湿度与室中央的温度之间的变化存在非线性关系。整体建筑内部热量传递的延迟是由于室内空气的不流通造成的。