裂隙白云岩流固耦合力学特性研究

刘德鹏， 饶军应， 王石光

(1.贵州省交通规划勘察设计研究院股份有限公司， 贵阳 550081； 2.贵州大学土木工程学院， 贵阳 550081； 3.中铁十八局第二工程有限公司， 唐山 064000)

近年来，随着交通建筑行业的快速发展，导致了岩土、边坡及隧道等工程方面的事故频发。岩体本身是一种天然地质材料，其内部常蕴藏裂隙、裂纹及节理等原始缺陷。地下岩体周围通常分布有应力场和渗流场，它们之间的相互作用使得裂隙、孔隙等萌生、扩展、贯通，从而威胁工程的安全。然而，如何通过应力-渗流耦合来描述岩体的受力状态或力学特性的异常变化是保障工程设计、施工、管养安全与质量的重要途径之一。

流固耦合模型是一种将应力场与渗流场结合的有效分析方法，表示岩体裂隙内部流体与应力的相互作用，学者们在这方面做了诸多多研究。刘佳佳[1]研究发现流固耦合模型可以描述瓦斯应力变化规律；周晓敏等[2]研究发现降低渗透系数与泊松比对围岩有效应力控制具有重要作用；陈勇等[3]研究发现边坡稳定性与流固耦合作用有关；马勇新[4]研究表明，流固耦合模型比传统的非耦合模型更能表征高气压藏渗流与岩体变形特生；王伟[5]研究表明，流固耦合模拟结果与实际值接近，且该模型可以描述滑坡现象；高虎军[6]研究表明，隧道衬砌应力的变化与流固耦合现象有关；张建营[7]研究发现边界压应力趋于稳定时，耦合模型产生的动力效应与实际相符；黄启翔[8]研究发现耦合模型可以描述煤与瓦斯突出的力学作用机理。综上所述，目前学者们多基于弹塑性原理、介质的有效应力原理、张量定理等开展对应力-渗流耦合模型的研究，侧重考虑水在裂隙中的渗流及其与裂隙岩体间应力的耦合关系，而针对注浆液在岩体裂隙中的扩散、凝结状态对工程的影响及注浆液与岩体裂隙间的相互作用等方面的研究较少。

为此，基于多孔连续介质的双重有效应力原理[9-12]，建立应力-渗流的计算模型，采用控制变量法对比分析渗流时间t、流体密度ρ及应力σ间的耦合作用规律，从而给出裂隙白云岩流固耦合作用下的力学特性，可为工程安全施工提供指导意见。

1 双重有效应力原理

刘忠玉等[13]、胡丹等[14]在一维固结模型基础上并继续研究基质的力学和物理特性，得到了更为合理的三维固结模型理论；李传亮[15-16]在研究土力学时发现了双重有效应力原理，即多孔介质岩体变形具有结构变形和本体变形，在进行多孔介质的应力分析时，规定如下：一是多孔介质发生结构变形时，骨架体积视为不变，考虑其排列方式的变化，变形量用；二是多孔介质发生本体变形时，骨架的体积发生变化，但其介质分子的排列方式不变。以双重有效应力原理为依据开展对裂隙岩体应力-渗流-时间耦合模型的研究。

基于多孔介质的本体有效应力，可表示为

(1)

基于多孔介质的结构有效应力，可表示为

(2)

有效应力σa为本体有效应力与结构有效应力的叠加，可表示为

(3)

(1)当φ→0时，介质结构较密，其物理化学性质与相同介质的固体材料性质相似，此时有

(4)

(2)当φ→1时，此时介质材料比较疏松，它的物理化学性质就不能采用固体的化学性质来代替，必须通过其他手段来确定其力学性质。则有

σa=δ-P

(5)

(3)根据双重有效应力原理可知，φ=0的介质是不存在的。

(4)双重有效应力原理主要用于多孔介质的岩体类结构，将其应用到流固耦模型之中，它能充分的考虑岩体的结构变形和本体变形，比单纯采用Terzaghi及Biot理论有效应力更能反映岩体的力学性质及变形机理。

2 应力场方程

假设多孔介质材料为各向同性、且有相等的弹性模量，其本构关系方程[17]为

εa=Mδa，a=x、y、z

(6)

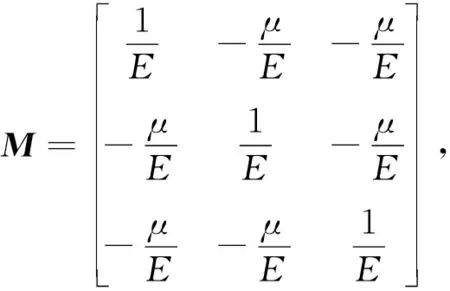
设ux、uy、uz分别为固体骨架x、y、z方向的位移，则得到几何方程为

(7)

将式(7)代入式(6)可得

(8)

(1)本体有效应力。利用矩阵叠加思想，视本体有效应力为三维坐标系下的应力组合，即式(1)，将式(8)代入式(1)得

(9)

(2)结构有效应力。利用矩阵论思想，将结构有效应力看成是三维坐标系下的应力组合，即式(2)，将式(8)代入式(2)可得

(10)

由多孔连续介质的双重有效应力原理知，总的有效应力等于本体有效应力与结构有效应力的之和，即将式(9)、式(10)代入式(3)得总的应力分量[式(11)]。

(11)

式(11)中：σa为本体有效应力与结构应力叠加应力，即双重有效应力；σax、σay、σaz分别为x、y、z方向上的双重有效应力分量。

式(11)是以ux、uy、uz、P为变量的平衡方程。从而可知连续多孔介质材料的双重有效应力是ux、uy、uz、P的函数，即σa=σa(ux、uy、uz、P)。

3 渗流场方程

设h为渗流场中各点的测管水头，根据Darcy定律，则有一点水力坡度降在3个坐标轴上的分量ix、iy和iz可表示为[18]

(12)

式(12)中：负号表示水力坡度降的正值对应测管水头降低的方向；ix、iy和iz为x、y、z方向水力坡度。

对于三维空间的渗流场，且岩土体为各项同性，故可得到流体的渗流速度为

(13)

式(13)中：k为土体的渗透性系数；υx、υy、υz为x、y、z渗流速度。

在某一小微元内，流体在渗流场中流速是稳定的，其体积为dxdydz，在x、y、z方向的流速分别为υx、υy、υz。根据能量守恒原理，在其微元内部必然存在一个内源压力q，使得整个渗流系统能量守恒。

根据双重有效应力原理，可得

(14)

流体连续性方程为

(15)

式(15)中：Θ为流体流量；t为时间。

流体状态方程为

ρ=βρ0e-βP

(16)

测管浆液水头等于压力水头与位置水头之和，可表示为

(17)

流体体积含水率与孔隙水压力关系为

(18)

将式(12)～式(18)代入Darcy定律可得

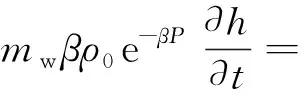
(19)

式中：ρ为流体密度，g/cm3；υ为渗流速度，m/s；ψ为水的动力黏度；ρ0为水的标准密度，ρ0=1 g/cm3；k为裂隙渗透系数，cm/s；β为水的压缩系数，Pa-1，取β=4×10-10Pa-1；Z为标高，m；mw为阻滞系数，一般情况取mw=1。

4 应力-渗流-时间耦合模型

为便于研究应力-渗流耦合模型与流体凝结或扩散时间之间的关系，视流体具有流动性、可压缩性、连续性等特点，且由式(12)可知，流体密度与流体压强之间存在一定理论关系，从而根据双重有效应力原理知，应力场与渗流场之间是相互影响的，即应力场的存在会影响流体凝结效果及在裂隙里的扩散效应，而渗流场的存在也会反过来影响应力场的性质，具体如图1所示。

图1 应力-渗流之间关系Fig.1 The relationship between stress and fluid seepage

结合式(17)、式(19)可推出式(20)，即

(20)

由式(14)得，依据矩阵间运算，解矩阵方程得各应力分量为

(21)

由式(16)流体状态方程得

(22)

式(22)中：ρ0、β均为常数，在式(22)等式两边分别对x、y、z求二阶导可得

(23)

结合式(20)～式(23)，记：

(24)

式(24)中：∇、Δ为换算符号。

化简得

(25)

式(25)即为流固-耦合方程，裂隙岩体在应力-渗流耦合时是关于时间t、坐标x、y、z的函数，即σ=σ(x、y、z、t)，可通过边界条件及积分进行求解。

5 模型求解及典例计算

5.1 模型求解

于实际工程项目而言，β、k、φ、φC、mw、ρ0、q、E及μ都是常数，由渗流知识可知，流体是位置坐标的一次函数[19]，即

(26)

设A、B、C、D4个参数，其取值分别为

(27)

从而将式(25)化简得

(28)

由E=σ/ε，将式(27)两边同时除以ε，即

(29)

取H=E2/D+BE/D，再次化简得

H=σΔρ

(30)

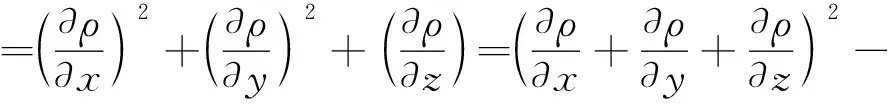
(31)

流体微分表示在极短时间内，可以将流体看作不变量，在某一瞬间，当流体流动时间Δt→0时有

(32)

将式(32)代入式(17)并积分得

化简得

(33)

从式(33)可知，σ与ρ、t有关，且流体密度越大，时间越大，流固耦合产生的应力就越小；流体密度小，时间越小，此时耦合产生的应力就越大。这与实际工程相符合，流体密度小、流体与围岩作用时间短，此时产生的基本是围岩初始应力，被流体分担的部分就变小，而流体具有稀释作用，流体密度及作用时间的变少，就意味着，围岩处于平衡状态，此时初始应力是很大的。

5.2 典例计算

以贵州境内某隧道为依托案例，该隧道为双洞单线式，全长925.411 m。资料显示：ZDK26+143.2～+300段覆盖层为块石层与红黏土层，下伏基岩为松子坎二段泥质白云岩，岩体较破碎，且节理裂隙较发育，呈浅灰色、灰白色，中厚层状，存在大量裂隙，其岩体物理力学性质如表1所示。

根据依托工程可知，裂隙白云岩的孔隙率φ为2%，有效孔隙率φC为0.5%，阻滞系数mw为1，将其已知参数代入式(27)，可得相关的物理参数计算如表2所示。

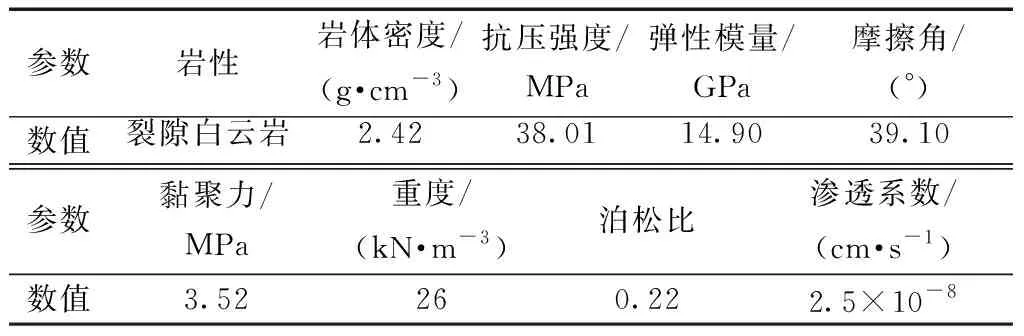
表1 岩体物理力学参数Table 1 Physical and mechanical parameters of rock mass

根据已知数据及σ、ρ、t三者之间的关系，以依托工程为基础进行数值模拟分析，对比分析在不同条件下的应力随时间、流体密度的变化规律及找出注浆液的最佳凝结时间，故采用相关编程软件，绘制出应力云图(图2)。

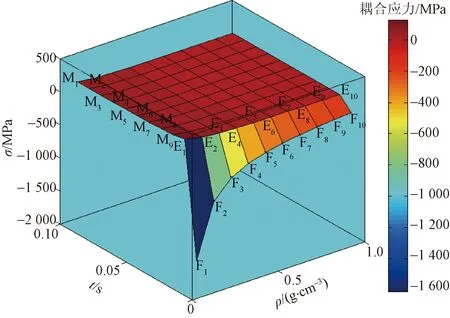
M1～M9、E1～E10、F1～F10为应力转点图2 应力-渗流耦合云图Fig.2 Stress-seepage coupling cloud diagram

由应力云图(图2)可知，耦合模型的应力大小与流体密度及时间均有关。应力值随着时间t、流体密度ρ的增加而增大，应力增大到一定范围后，应力值波动范围很小，甚至不变。

为更直观的判断应力-渗流耦合时间t及流体密度ρ对耦合应力的影响情况，这里采用控制变量法进行研究，即控制流体密度不变，改变耦合时间t，绘制σ-t曲线，如图3所示；控制耦合时间不变，改变流体密度，绘制σ-ρ曲线，如图4所示。

由图3可知：流体密度不变时，耦合模型的应力值随耦合时间的增大而增大，且作用时间越长，产生的应力峰值就越小。当t=0.02 d时，每种流体密度在σ-t曲线上均出现应力最大值，在此之后，应力值基本不随时间变化而变化。

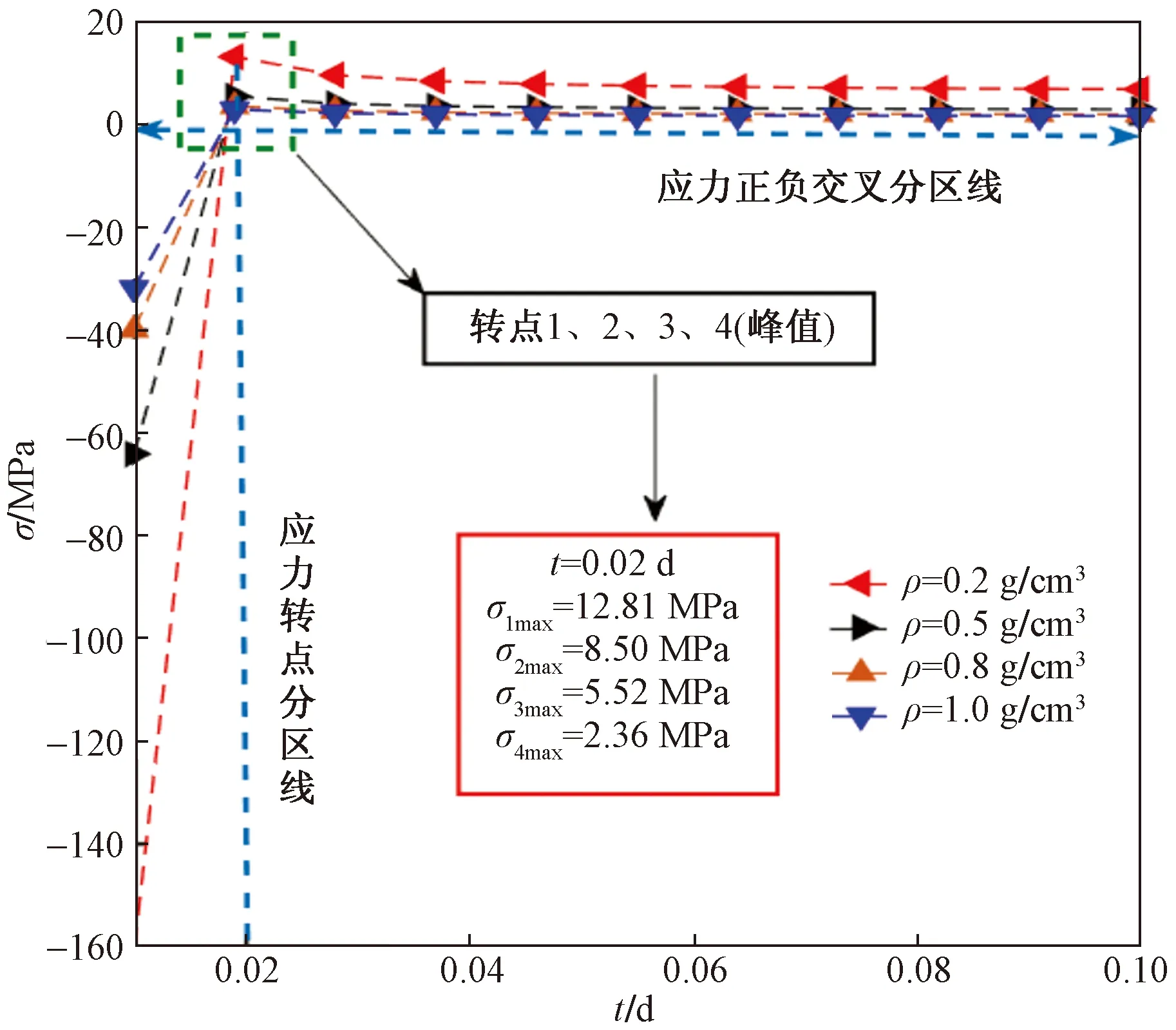
σ1max、σ2max、σ3max、σ4max分别为在t=0.02 d时转折点 1、2、3、4对应的峰值应力图3 σ-t曲线示意图Fig.3 Schematic diagram of σ-t curve

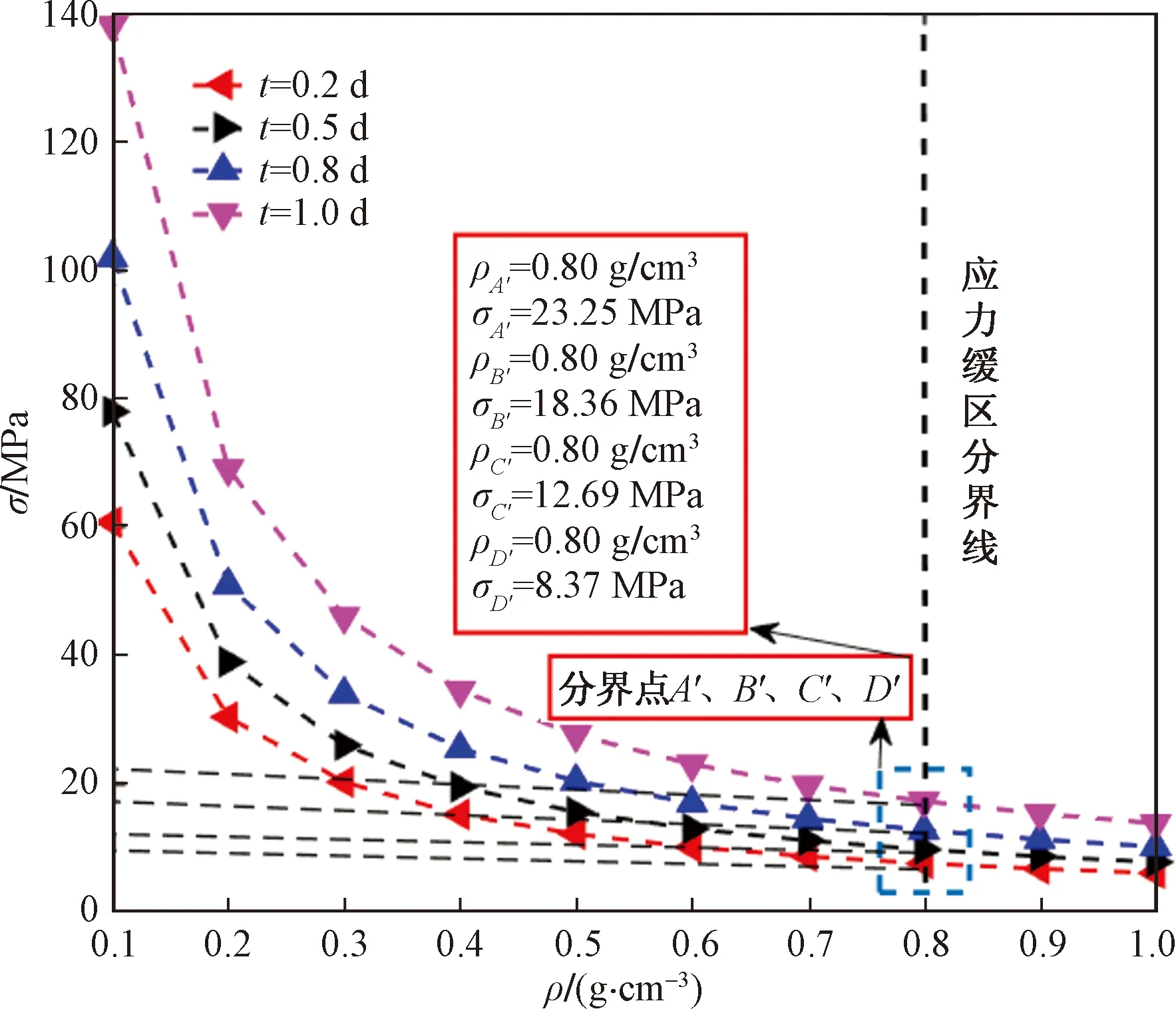
σA′、σB′、σC′、σD′分别为在分界点A′、B′、C′、D′对应的耦合应力； ρA′、ρB′、ρC′、ρD′分别为在分界点A′、B′、C′、D′对应的流体密度图4 σ-ρ曲线示意图Fig.4 Schematic diagram of σ-ρ curve

由图4可知，在控制时间不变情况下，耦合模型产生的应力值随流体密度的增加而减少，当增加ρ为0.8 g/cm3时，应力值基本不变。当ρ为0.2 g/cm3时，每种时间对应下的σ-ρ曲线均产生应力最大值。

表2 裂隙白云岩相关参数Table 2 Related parameters offractured dolomite

为确定应力开始变缓时的时间t及流体密度ρ，进行数值分析时分别取了3个不同应力增幅进行研究，且将数值解和理论解进行对比，如图5所示。

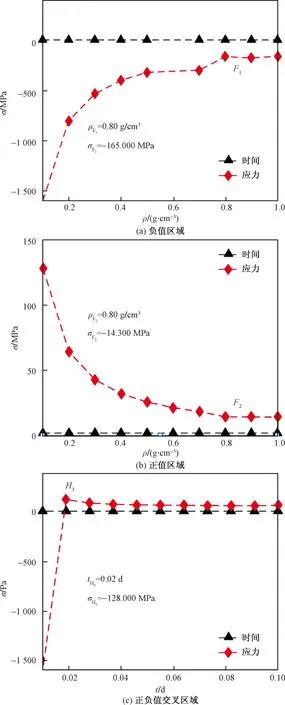
ρF1、 ρF2分别为在标记点F1、F2对应的流体密度； σF1、σF2、σH3分别为在标记点F1、F2、H3对应的耦合应力； tH3为标记点H3对应的时间图5 各区域应力变化Fig.5 Stress changes in each area

图5(a)表明：在负值增值幅区域，应力的大小随流体密度的增加而增加，当流体密度增加到0.8 g/cm3时，此后应力增幅变缓，应力基本不变。说明应力值σ随流体密度ρ的增加不是无限制的，结合图3可知，无论耦合时间时长多少，流体密度ρ为0.8 g/cm3为该耦合模型应力增幅基本不变的分界点，即H1点。

由图5(b)可知，在正值增值幅区域，应力值随流体密度的增加而增加，当流体密度ρ为0.8 g/cm3后，应力增幅变缓，应力趋势线接近水平线。说明应力值σ随流体密度ρ的增加不是无限制的，结合图3可知，无论耦合时间为多少，流体密度ρ为0.8 g/cm3为该耦合模型应力增幅基本不变的分界点，即H2点。

由图5(c)可知，在正负应力增值区域，应力的大小随耦合时间的增加而增加，当t为0.02 d后，此时应力达到峰值，应力增幅基本不变，应力趋势线也接近水平线。说明应力值σ随耦合作用时间t的增加是有限的，且结合图2可知，无论流体密度ρ为多少，t为0.02 d时为该耦合模型应力增幅基本保持不变的分界点，即H3点。

图3～图5共同说明，应力值随流体密度ρ、时间t的增加而增大，且在t为0.02 d、ρ为0.8 g/cm3之后，应力值基本保持不变，应力趋势线也近似看作是水平线。

6 结论

(1)应力场与渗流场方程理论推导过程，考虑岩体变形特征、流体密度、位置坐标、流体压力及渗流时间等因素，采用流体密度变分方法，建立了应力-渗流-时间等多场耦合理论分析模型。

(2)经理论分析发现，应力-渗流-时间多场耦合时，应力、流体密度及渗流时间是相互制约、相互影响的，且存在数值对应关系。

(3)通过实例分析，流体密度及时间使裂隙白云岩力学特性发生较大变化，且当0.01 d

(4)该模型在前人研究基础上，增加了时间变量、岩体结构变形及本体变形本构关系和流体密度对时间、位置坐标的变分等对模型建立的影响，但该模型视渗透系数、裂隙宽度、孔隙度为常数，后续研究可将渗透系数、裂隙宽度、孔隙度等考虑在内，其围岩应力变化情况有待研究。

(5)虽然对贵阳某地区裂隙白云岩力学特性进行数值分析，但本文模型的理论推导是基于一般裂隙岩体，所以该耦合模型也可为其他裂隙岩体流固耦合模型理论推导提供参考。