25 A有源电力滤波器主电路参数设计与仿真研究

胡春龙

(陕西国防工业职业技术学院，陕西 西安 710300)

0 引言

随着电力电子技术的不断发展，各种功率器件被大量应用于电能变换装置中，使得谐波污染在公用电网中愈演愈烈，从而导致电能质量下降，传输效率变低。有源电力滤波器(active power filter，APF)作为谐波补偿装置，可以实现对谐波的动态补偿，具有高可靠性和抗扰性，从而在电力系统中得到了广泛应用[1]。但APF的补偿性能却与其主电路参数的设定有着密切关系，包括直流侧电压、直流侧电容和交流侧滤波电感等，它直接关乎着补偿装置的硬件选型和补偿效果，故如何准确选取主电路参数对APF的高效率工作极为重要[2]。

本文按照补偿电流跟踪法设计了直流侧电压和直流侧电容，同时结合抑制开关频率处的谐波要求设计了交流侧滤波电感，设计方法简单、可靠，避免了经验法和模型法确定参数的不确定性和复杂性。

1 并联型APF拓扑结构

并联型三相三线制APF拓扑结构如图1所示。图1中，usa、usb、usc分别为网侧三相交流电压；isa、isb、isc分别为网侧三相交流电流；iLa、iLb、iLc分别为三相负载电流；R1、L1为负载等效电阻电感；ica、icb、icc分别为APF输出三相补偿电流；uca、ucb、ucc分别为APF三相输出电压；L为APF三相滤波电感；Cdc为直流侧滤波电容；Udc为直流电压；S1～S6为APF桥臂功率器件[3]。

图1 并联型APF拓扑结构

APF的输出状态取决于功率器件的开关状态，定义开关函数Sk(k=a,b,c)=1为上桥臂接通，下桥臂关断;Sk(k=a,b,c)=0为上桥臂关断，下桥臂接通[4]。由电路的基本定则可知

(1)

R为APF线路输出等效电阻。根据三相电网电压电流对称性可知

(2)

uN为中性点电压。对直流滤波电容Cdc侧应用基尔霍夫电流定则可知

(3)

结合式(1)～式(3)，可得并联型三相三线制APF数学模型为

(4)

2 APF主电路参数设计

APF系统给定参数为：三相交流电网电压u=380 V，额定输出电流i=25 A，开关频率f=40 kHz。在此给定参数下，对主电路参数进行设计。

2.1 直流侧电压设计

为了提高APF的补偿性能，APF的输出补偿电流应始终与指令电流的变化保持一致。以APF的A相输出为例，在忽略线路电阻的情况下有

(5)

ica为逆变器A相输出补偿电流；usa为A相电网电压；Sa为开关函数；Udc为直流侧电压。

(6)

由式(6)经变形后可得

Udc>3usa

(7)

从式(7)可以看出，直流电压应大于电网相电压的3倍以上，APF输出补偿电流对指令电流的跟随性，将随着直流电压Udc的增大而增强，但Udc的变大对功率开关器件的耐压性提出更高要求[5]。代入数值后，综合考虑取Udc=700 V。

2.2 直流侧电容设计

根据能量守恒及工程实际经验公式有

(8)

Udc为直流电容侧电压；iN为系统额定电流值；k为直流电压的波动系数，取0.01～0.1；η为补偿能量系数，取0.2。代入式(8)中得

这里选取直流电容容值为2 200 μF。

当直流电压取700 V时，在选取2 200 μF电容时，直流电压波动为700×0.01=7 V左右。在后面仿真结果中进行验证。

2.3 交流侧滤波电感设计

在对APF输出滤波电感进行参数设计时，有2个条件同时满足：一是为了达到补偿电流跟随指令电流快速变化的目的，滤波电感在设计时数值不能太大；二是从降低开关频率处的谐波出发，滤波电感在设计时数值不能太小[6]。下面分别从这2个要求出发，对滤波电感进行设计。

2.3.1 从对补偿电流跟随性要求设计L

指令电流选取第n次谐波时，分析补偿电流的跟随性，为了达到补偿效果，补偿电流需与指令电流的变化保持一致。n次谐波变化率在过零点处达到最大值，要求滤波电感在该时刻应为最小值，以A相为例，计算此刻补偿输出电流，定义从逆变器侧流向网侧的电流方向为正方向，A相桥臂上下功率开关管的开关状态决定了补偿电流的增大和减小过程[7]。开关状态对应的补偿电流变化情况如图2所示。

图2 补偿电流随开光状态变化情况

从图2可以看出，补偿电流在跟随指令电流变化时，其增量应始终保持大于或等于指令电流，即电流曲线斜率应在指令电流之上。只有这样才能确保在1个开关周期内补偿电流在指令电流附近很小范围内波动，可表示为

(9)

Inm为第n次谐波幅值。又知，在1个开关周期内有

(10)

(11)

2.3.2 从抑制开关频率处的谐波来设计L

当n次谐波电流上升到最大值时，谐波电流变化率在此时为最小值，而补偿电流波动在此时却是最大值，可认为此时|Δiup|=|Δidown|，脉动达到最大，即Δiup+Δidown=0，在此时分析电感取值范围下开关频率处谐波抑制的过程[8]。以A相为例，补偿电流波动在指令电流峰值附近时达到最大值，如图3所示。

图3 补偿电流变化情况

由于主开关器件一般工作在高开关频率下，而网侧电压和指令电流相对于主开关频率变化较为缓慢，一般可认为两者在1个开关周期内是恒定的，输出补偿电流有如下关系，即

(12)

由|Δiup|=|Δidown|，设Δiup>0，Δidown<0，对于开关周期有Tup+Tdown=T，又Δiup+Δidown=0，且在Tdown=T-Tup时，可得Tup的表达式为

(13)

结合式(12)和式(13)可求得Δiup的表达式为

(14)

|Δiup|为补偿电流的最大脉动；fsw为开关频率。

若在开关频率处补偿电流脉动允许的最大值为Δimax，则由|Δiup|≤Δimax可计算出此时滤波电感的取值范围为

采用分层整群取样的方法，使用问卷进行现场调查。调查员分批进入学生宿舍进行问卷调查和访谈，向同学阐明本次调查的目的和意义。以不记名的形式由学生填写后当场收回。调查内容包括：班级、性别、就读护理学专业的原因，是否第一志愿就读本专业，是否考虑过转专业，对护士工作三班倒的态度，如何评价护理专业老师授课水平，对护理工作前景的看法等项目。共发放调查问卷520份，收回有效问卷510份，有效率达98.07%。

(15)

结合式(11)和式(15)，可得既能满足对指令电流跟随性的要求，又能满足对开关频率出谐波抑制的要求的滤波电感取值范围为

(16)

其中，取能补偿到的最高次谐波n=7，Inm取到基波峰值电流的1.5倍，Δimax取到基波峰值电流的10%，这样可得

同时结合式(16)，得499.3 μH≤L≤1 115.9 μH。综合考虑选取滤波电感的感值为1 000 μH。

3 仿真结果与分析

3.1 仿真模型建立

按照设计的主电路参数，在MATLAB/Simulink仿真环境下建立了三相并联型有源电力滤波器仿真模型，仿真模型结构如图4所示。

图4 三相并联有源滤波器仿真模型

根据APF控制要求，设置相应的仿真条件，系统仿真条件设定如表1所示。

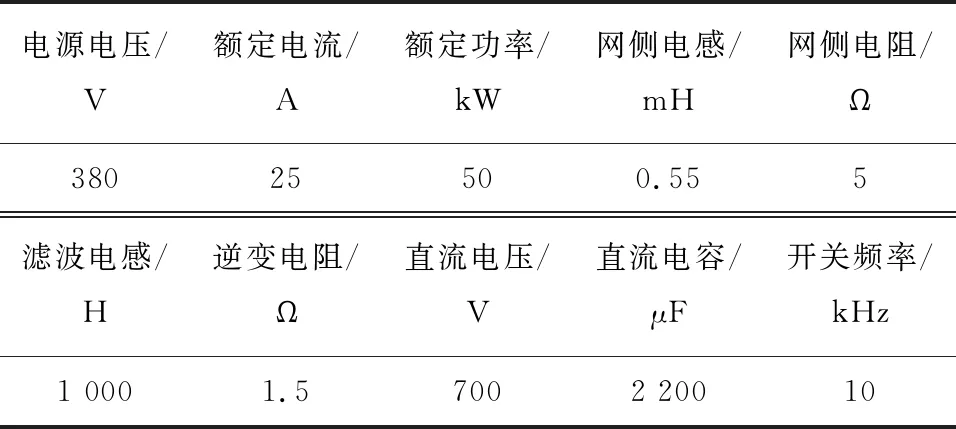
表1 仿真参数

3.2 仿真结果

从图5可知，直流电压能够快速跟随给定电压，稳定在700 V左右，直流电压上下波动约为4 V，在理论计算的波动范围内。

图5 直流电压曲线

7次谐波电流跟随性对比波形如图6所示。其中，7次谐波电流给定为正弦信号，逆变器输出电流带有毛刺且跟随给定信号而变化。

图6 输出电流跟随谐波电流变化曲线

从图6可以看出，系统输出谐波电流能够较好的跟随给定电流的变化而变化，跟随性能良好。

流过滤波电容C的电流如图7所示；电流经过傅里叶分析(FFT)后，在500 Hz内的谐波电流含量如图8所示。

图7 流过滤波电容的电流

图8 电流的FFT分析

从图7和图8可以看出，流过滤波电容的电流有基波、7次谐波和较高次谐波电流。

流过滤波电感L的电流即系统输出电流如图9所示；电流经过傅里叶分析(FFT)后，在500 Hz内的谐波电流含量如图10所示。

图9 流过滤波电感的电流

图10 电流的FFT分析

从图9和图10可以看出，流过滤波电感的电流即系统输出电流中，只含有基波、7次谐波电流，而高次谐波电流明显得到了滤除。

4 结束语

主电路参数不仅影响着APF的补偿性能，而且在器件选型和设备成本方面也有重要作用。本文以额定电流为25 A的并联型三相有源电力滤波器为研究对象，在分析了APF拓扑结构和数学模型的基础上，选取了不同的设计方法对直流侧电压、直流侧电容和滤波电感3个重要主参数进行了设计。按照设计参数在MATLAN/Simulink中对APF进行了仿真分析，结果表明参数设计合理有效，谐波电流补偿性能得到显著提升。