基于多目标的刨切机床身结构优化设计
任 旺,刘芳华,仲昭杰,郭文龙,吴万毅
(江苏科技大学机械工程学院,江苏 镇江 212100)
0 引言
床身作为刨切机重要的基础支撑部件,其动静态特性直接影响着整机的加工精度、稳定性和可靠性[1]。为保证刨切机能满足高精度、高效、稳定的工作要求,对床身进行合理的结构优化设计以提高其力学性能尤为重要。
传统刨切机床一般依靠经验进行结构设计,由于设计理论基础的不足,为了保证机床工作性能,设计参数会比实际需要的更大一些,就会造成重量大、耗材高等问题,而且往往结构上也难以实现最优化。随着有限元分析技术和新优化算法的发展,结构优化设计效率大大提高。目前,国内外学者普遍采用尺寸优化的方法应用于机床的结构设计与优化中。郑彬等[2]通过模态分析确定某铣床床身的薄弱处,对其主要尺寸进行试验设计、灵敏度分析并建立响应面模型,利用多目标优化算法对其结构优化;甘盛霖等[3]针对某磨床床身,通过灵敏度分析确定影响床身静动态特性和整体质量的主要参数,对床身内部筋板厚度和布局方式进行尺寸优化,得到了最佳结构优化方案;杨志贤等[4]通过正交实验法建立了响应面模型,采用遗传算法对其多目标优化求解,并基于信息熵赋权的多目标灰靶决策算法进行解集优选;刘峰等[5]采用实验模态测试确定出某机床的工作台为薄弱环节,将灵敏参数作为设计变量,以低阶固有频率、质量和刚度为优化目标进行尺寸优化;薛会民等[6]利用尺寸优化和拓扑优化方法,对床身进行以减轻质量和提高刚度为目标的结构优化。
本文以某数控刨切机床身为研究对象,进行静力学分析和模态分析,以床身质量、最大静变形和一阶固有频率为优化目标,对设计参数进行灵敏度分析并建立响应面模型,采用遗传算法对床身主要设计参数进行多目标优化,为提高床身性能打下基础。
1 床身静动态特性分析
1.1 床身静力学分析
床身内部采用布置筋板的结构方式,其中床身前端有2块主筋板和4块副筋板,床身后端内部有6块横向筋板,底部的支撑面由6个地脚螺栓进行固定,床身上部的螺纹孔用于安装固定工作台、刀架等其他零部件。
床身采用的材料为灰铸铁HT250,其材料属性:密度为7 200 kg/m3,弹性模量为110 GPa,泊松比为0.28[7]。为方便网格划分,提高运算效率,有必要对床身模型上的螺纹孔、圆角、倒角以及凸台等对分析结果影响较小的特征进行简化或忽略,再将简化后的模型导入到ANSYS Workbench中进行网格划分,采用四面体单元对床身进行网格划分。
在进行静力学分析时,床身上受到的载荷主要为自身的重力和安装在床身上的工作台等其他零部件的质量,床身底部通过螺栓进行固定约束。经计算求解,得到静力学分析结果如图1所示。
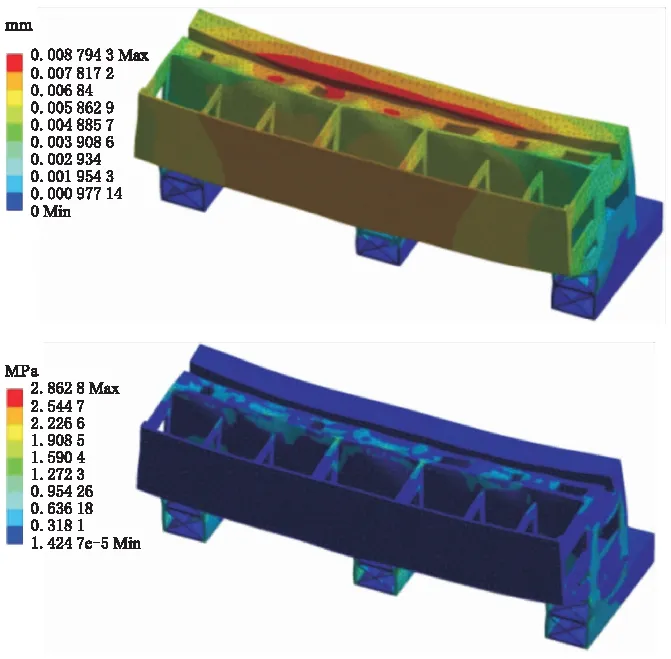
图1 静力学分析结果
由图1可知,最大变形位于床身上部与安装其他部件的连接处,变形量最大为8.794 3 μm,最大应力位于床身底座连接处以及内部各筋板接触部位,最大应力为2.862 8 MPa,远小于材料的强度极限,可知床身设计有较大的余量,对床身结构需要进一步优化,以提高其动静态性能。
1.2 模态分析
在对床身模态分析时,不需要考虑施加任何载荷,只需对床身底部螺栓进行固定约束。机床在工作过程中,当在外部激振频率接近床身固有频率,会产生共振现象,对机床加工的精度和稳定性有重要影响,应避免接近振动频率范围。低阶模态是影响机床动态性能的主要因素,因此提取床身的前4阶模态进行分析,其前2阶振型如图2所示,前4阶振型和固有频率如表1所示。
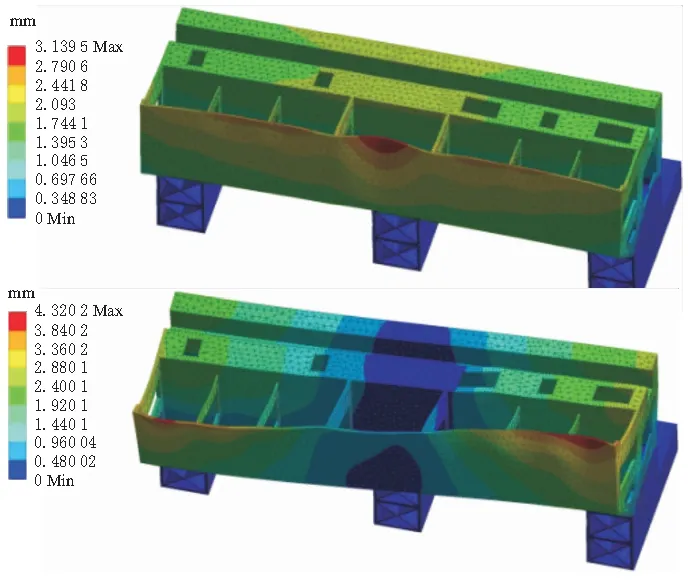
图2 床身前2阶振型

表1 床身前4阶固有频率和振型
2 响应面模型的建立
2.1 设计变量的选择
床身尺寸参数较多,不可能选取每个参数进行优化。为此需要考虑影响床身性能较大的参数,将床身前后端外部壁厚、前后端内部筋板厚度等5个参数作为设计变量,如图3所示。
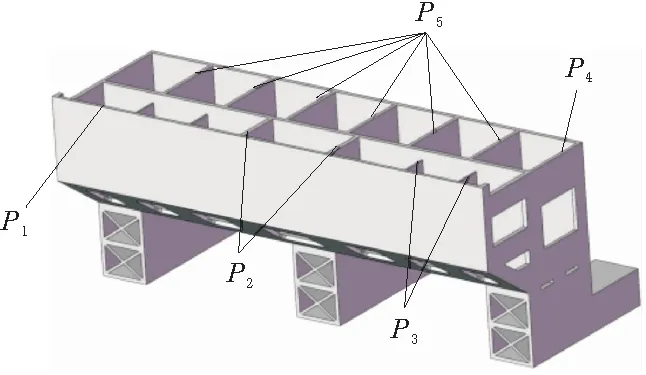
图3 床身设计参数
在床身原有结构不变的基础上,确定设计变量参数的取值范围,参数及变化范围如表2所示。

表2 设计变量及参数变化范围
2.2 DOE试验设计
在ANSYS Workbench的Design of Experiment模块中对床身进行拉丁超立方试验设计,系统自动生成27组样本数,以床身质量P6、静态最大变形量P7和一阶固有频率P8为输出参数,部分样本点及试验结果如表3所示。

表3 部分样本点及试验结果

表3(续)
2.3 响应面分析
响应面法是结合数理统计原理,通过试验设计对指定样本点集合进行试验分析,得到设计变量的目标函数与约束函数的响应面模型,来预测非试验点的响应值[8]。本文选用二阶响应面模型,即
(1)
Y(X)为输出变量;X为设计变量;n为设计变量的个数;α0、αi、αij为未知系数,由最小二乘法求解确定。
为评价响应面模型质量,利用参数R2来评估响应面拟合精度,当R2接近1时,表明响应面拟合精度较高[9]。
(2)
(3)
(4)

图4~图6分别为设计变量P1、P4与质量的响应面、设计变量P4、P5与最大静变形的响应面、设计变量P1、P4与一阶固有频率的响应面。

图4 设计变量P1、P4与质量的响应面

图5 设计变量P4、P5与变形量的响应面

图6 设计变量P1、P4与一阶固有频率的响应面
由图4可知,随着床身前后端外部壁厚P1、P4的增大,质量也随之增大;由图5可知,随着床身后端外部壁厚P4和横向筋板厚度P5的增大,最大静变形迅速减小;由图6可知,当床身前后端外部壁厚P1、P4在最大值时,一阶固有频率最小。根据响应面图分析可知各个设计变量对输出参数的影响,在为后续设计变量优化时,需综合考虑设计变量对床身结构性能的影响程度,选择合理的设计方法,以寻求最佳参数组合,使其性能达到最优。
2.4 灵敏度分析
在进行结构优化时,床身结构性能(输出参数)一般由多个设计变量相互作用决定的,经由灵敏度分析可以确定设计变量对输出参数的影响程度,选取对输出参数影响显著的设计变量作为关键变量进行优化设计。经分析得到各设计变量对输出参数的灵敏度,如表4所示。

表4 各设计变量对输出参数的灵敏度
在进行灵敏度分析时,当设计变量为正值时,设计变量对输出参数成正相关;当设计变量为负值时,设计变量对输出参数成负相关。由表4可知,床身后端外部壁厚对床身质量影响最大,其余设计变量影响较小;床身后端壁厚和内部横向筋板厚度对最大静变形影响较大且成负相关,主要由于最大静变形集中在床身上部;只有内部横向筋板厚度对一阶固有频率成正相关,其余设计变量对其成负相关,床身前后端壁厚对其影响较大,主要原因是一阶振型为床身横向摆动。
3 床身多目标优化
3.1 床身多目标优化数学模型
以床身质量、最大静变形和一阶固有频率为优化目标,选取好设计变量参数,设定其参数变化范围,建立多目标优化数学模型,可表示为:
min[m(X),fd(X),-ff(X)]
X=[x1,x2,x3,x4,x5]T
s.t.xim≤xi≤xin,i=1,2,…,5
m(X)为床身质量;fd(X)为最大静变形;ff(X)为一阶固有频率;x为设计变量;xim、xin分别为各设计变量的上限值和下限值。
3.2 基于遗传算法的多目标优化
采用多目标遗传算法(MOGA)[10]对优化目标进行优化求解。以床身质量最小、最大静变形最小和一阶固有频率最大为优化目标,进行多目遗传算法的优化求解,经求解得到一系列Pareto最优解。在Pareto解集中选出的3组最佳优化解,如表5所示。

表5 最佳优化解集
3.3 多目标优化结果分析
根据对设计目标的要求,经过对比分析,从中选择1组效果较优的参数作为优化结果,对参数进行圆整,优化前后设计变量的参数对比结果如表6所示。

表6 优化前后参数对比
对优化后的床身进行动静态特性分析,优化前后的结果对比如表7所示。
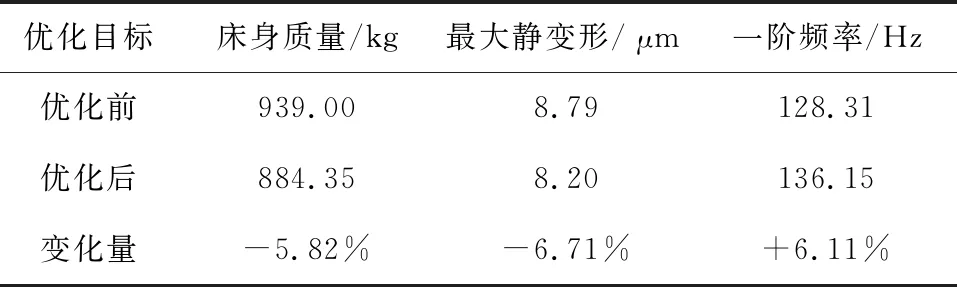
表7 优化前后结果对比
由表7可知,床身质量减少了54.65 kg,优化后的床身质量减幅为5.82%;优化前的最大静变形为8.79 μm,经优化后最大静变形为8.20 μm,减幅为6.71%;一阶固有频率提升了6.11%。在床身质量减轻的基础上,床身的最大静变形和一阶固有频率均得到明显优化。
4 结束语
本文以某刨切机床身为研究对象,提出一种基于灵敏度分析的多目标优化设计方法。对床身进行有限元分析,找出床身的薄弱部位;针对床身外部壁厚、内部各筋板厚度进行拉丁超立方试验设计,通过灵敏度分析并建立响应面模型,确定了各设计变量对床身质量和床身动静态特性的影响程度;以降低床身最大静变形和质量,提高一阶固有频率为优化目标,采用多目标遗传算法对床身进行优化并得到最佳优化解集。在减轻床身质量的同时,提高了床身结构性能。该设计方法为床身的优化设计和改造效率的提升提供一定理论依据。

