农田水利设备中抽水泵机械振动故障检测方法

孙兆光

(莒县青峰岭水库管理服务中心，山东 莒县 276500)

0 引言

机械故障检测技术[1-2]可对设备故障状态作出诊断，全面提升设备可靠性和安全性，其中，抽水泵机械设备广泛应用于农田水利设备中。随着社会进步和生产力的发展，抽水泵机械的应用更加广泛，但受到不同因素影响，抽水泵机械会产生不同类型的故障，导致设备的生产效率下降或部分功能丧失。如何确保抽水泵机械的稳定运行成当前研究的热点话题，国内相关专家给出了一些较好的研究成果。

任世锦等[3]将集成局部均值分解和改进的支持向量机相结合，将故障信号分解为多个单模态调制信号，加强故障特征提取的有效性，实现机械故障诊断；郑直等[4]对信号实施AMD分解，提取故障分量信号，将其作为特征向量，采用变分模态分解和模糊C均值聚类的方法分析信号，实现故障信号检测；武立平等[5]通过IMF能量特征，构建对应二元特征向量，分析变压器振动信号的特征向量变化情况，最终完成故障检测。但现有方法中考虑的参数较少，均存在一定局限性。

为此，本文提出一种农田水利设备中抽水泵机械振动故障检测方法。

1 农田水利设备中抽水泵机械振动信号特征提取

1.1 农田水利设备中抽水泵机械振动信号去噪

采用多分辨分析可更好完成信号时频分析，但由于尺度函数需要按照二进制变化规律执行，在频数较高的阶段会出现分辨率较差的情况，只可完成信号的频段划分。

在多分辨率中分析得到解空间M2(S)，可表示为

(1)

j为尺度因子；X(j)为小波子空间。

将尺度空间和小波子空间两者统一表征，即

(2)

W(j)为尺度空间。

设定{vn(t)}为关于序列{ik}的小波包簇，使用以下方式组成子空间簇，即

(3)

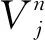
使用小波包可对农田水利设备中抽水泵机械振动信号实施正交分解，详细操作步骤如下所述：

a.将农田水利设备中抽水泵机械振动信号第1次分解结果的高频部分和低频部分，采用二抽取计算，确保偶数或奇数部分有效保留。

b.在进一步分解前，不仅需要再次分解高频部分，同时仍然采用二抽取计算，使其在任何频段均可获取相同时频分辨率。

c.重复上述操作过程，直至全部抽水泵机械振动信号完成分解。

d.将各个频率段上的信号重构，滤除抽水泵机械振动信号中的噪声，最终实现信号去噪[6-7]。

1.2 农田水利设备中抽水泵机械振动故障特征提取

在上述抽水泵机械振动信号去噪后，对农田水利设备中抽水泵机械频谱分析过程中，需要寻找带有明显转频特征的频谱图。

a.实际频率g(i)提取。在信号理论频率g(s)附近随机小区间[x1,y1]内提取最高幅值对应频率。

b.在振动信号幅值谱随机区间内，获取实际频率外其他极大值点，同时采用降序的方式排列。

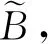
(4)

n为极大值的数量；B(i)为第i个极大值。

d.设定敏感性指数，即

(5)

T和Tmax分别为敏感性指数和最大敏感性指数，主要反映实际转频幅值和周围高幅值频率成分之间的相对水平。

在此基础上，分析抽水泵机械振动信号，通过抽水泵结构特点选择10个测点，获取振动信号的变化规律[8-9]。

引入复杂度概念，描述时间序列变化情况，对不同测点复杂度通过二值粗粒化方法以及四值粗粒化方法计算。由于通过阶跃函数定义不同序列之间的相似性，但序列和实际样板类边缘存在模糊不清情况。其中，模糊熵的详细操作步骤如下所述：

a.组建维数为m的向量，即

(6)

k0(i)为向量的平均值。

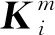
(7)

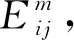
(8)

d.将维数增加至m+1，同时重复步骤a～步骤c，获取对应函数的取值，表达式为

(9)

φ(m+1)(x,y)为函数取值。

模糊熵[10-11]需要将原始序列映射到维数较高的空间中，同时借助幅值的取值范围计算不同序列复杂度，采用模糊函数获取不同序列之间的相似性，确保最终获取的计算结果和实际结果更加吻合。

采用模糊熵提取农田水利设备中抽水泵机械振动故障特征，获取时域特征参数可以表示为

(10)

H为时域特征参数；Tx为概率密度函数；p(x)为抽水泵机械振动幅值。

1.3 抽水泵机械振动故障检测实现

在抽水泵机械振动故障检测中，对目标测试样本比较少的情况，无法有效训练1个泛化能力比较强的分类器，导致对故障数据的检测有限。因此，本文将多层支持向量机学习模型和样本迁移深度迁移算法相结合，通过引入大量和目标诊断对象分布特征故障数据完成目标故障检测。

选取LSSVM作为多层结构基本学习单元[12-13]，在仅少量训练目标情况下，对于一般二分类而言，主要通过源域和目标域样本训练输入层，完成样本权值分配和特征学习，完成样本重构，即

s(i)=xiyizi(si,xi)+b

(11)

s(i)为样本重构结果；xiyizi为测试样本；(si,xi)为训练样本对应的标签；b为随机常数。

按照顺序对全部训练集中的样本实施转换处理，获取数量为N的全新训练样本，将其设定为下一层的输入，样本标签整个过程不发生任何改变。

当模型建立后，针对测试样本v而言，需要经过多层转换，最终获取输出对应的求解公式为

(12)

v(x)为输出求解结果。

在此基础上，建立样本迁移对应目标函数。其中，迁移算法核心操作思想为：通过不同目标域数据，根据重新分配源域和目标域训练样本权重，全面提升分类结果准确性。

对于随机1组训练数据集而言，经过优化后的目标函数可以表示为

(13)

minR(i,j)为目标函数；h(xi,yi,zi)为惩罚因子；M为惩罚函数。

在优化目标函数中增加源域样本，可有效改进损失函数，经过改进后的损失函数可以表示为

(14)

minR′(i,j)为改进后的损失函数。

源域和目标域之间的迁移学习是通过损失函数完成，其中，SVM的样本迁移原理可以表示为

(15)

ωt为目标域训练样本的权重向量取值；ω为源域中训练样本的权重取值。

为了更好地完成基于样本迁移的多层SVM[14-15]，在目标函数中同时对2个目标域的样本展开训练。通过LSSVM检测抽水泵机械振动故障，详细操作步骤如下所述：

a.确定网络层数和相关参数。

b.将所有样本标准化处理。

c.将全部样本放置到输入层中。

d.采用迁移学习完成输入层训练，对优化目标函数求解，同时完成样本重构。

e.重构样本，同时将其应用于下一层的训练，重复以上操作步骤。

f.逐层训练至输出层，求解分类判别函数；计算测试样本集的预测标签。

g.输出故障分类结果，完成抽水泵机械振动故障检测。

2 实验分析

2.1 实验方案

为了验证所提农田水利设备中抽水泵机械振动故障检测方法的有效性，需要开展相关实验。抽水泵在正常运行情况下的信号频谱变化情况如图1所示。

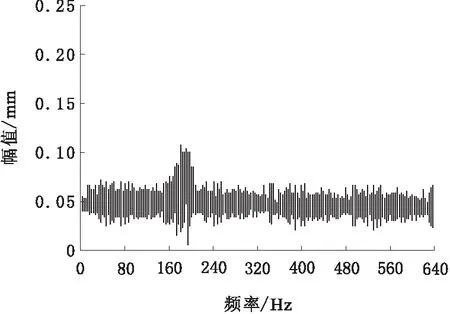
图1 抽水泵正常运行情况下信号频域曲线

由图1可知，在抽水泵正常运行情况下，会出现比较小的波动，但不会对抽水泵的运行产生影响。

为有效模拟抽水泵运行时产生的故障，需要在出口位置放置1个小型的木块，确保水泵拥堵。经过人为制造故障之后，获取的故障运行频谱如图2所示。

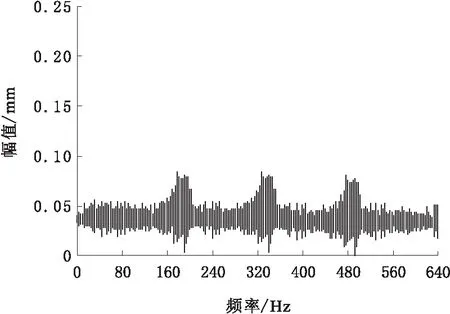
图2 抽水泵故障情况下信号频域曲线

2.2 实验结果分析

采用本文方法监测某抽水泵的机械振动故障信号变化情况，详细检测结果如图3所示。

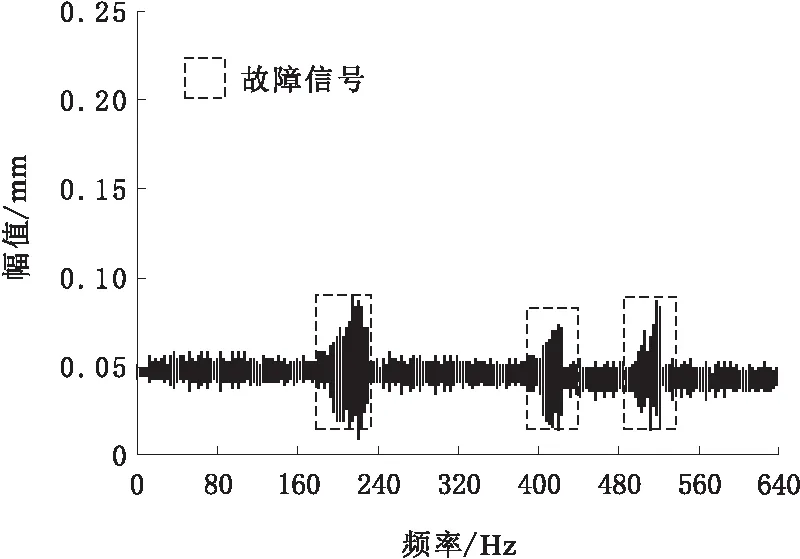
图3 抽水泵故障检测

通过图3可知，采用本文方法可以准确检测抽水泵的故障，获取准确的检测结果。

将正常信号频谱图和故障信号频谱图在低频段放大，采用本文方法对2种信号对应的局部频谱进行检测，得到的结果如图4所示。

分析图4中的实验数据可知，故障信号的尖峰比较明显，由此可以看出采本文方法可准确区分正常信号和故障信号。

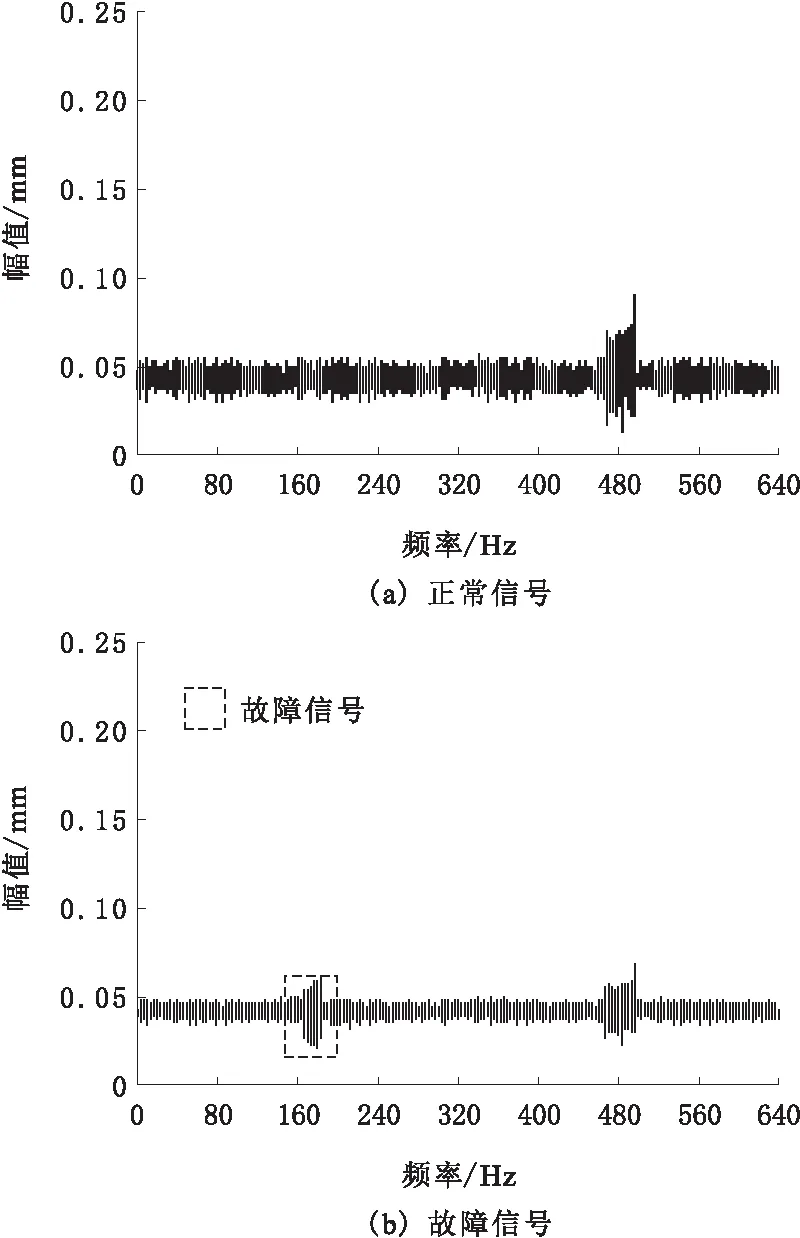
图4 正常信号和故障信号的局部频谱

为了验证本文方法的有效性，实验分析机械信号去噪前后的幅值变化情况，结果如表1所示。

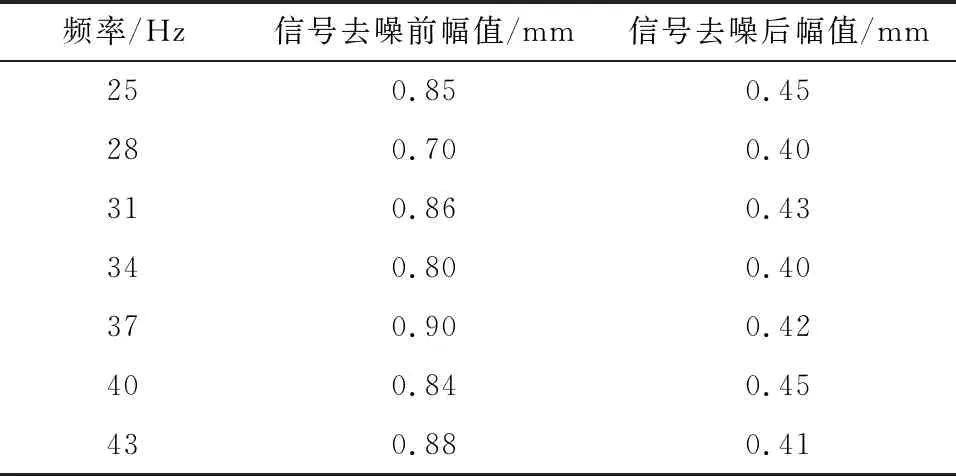
表1 抽水泵机械振动信号处理前后幅值变化情况

由表1可知，在信号经过去噪处理后，信号中的噪声得到有效滤除，可以有效降低幅值，同时获取更加准确的故障检测结果，验证本文方法的有效性。

3 结束语

针对传统抽水泵机械振动故障检测中存在的一系列问题，提出一种农田水利设备中抽水泵机械振动故障检测方法。经实验测试证明，该方法可以准确完成抽水泵机械振动故障检测。