非接触式功率传输滑环热力学仿真与分析
吴恢悦,付 庄,冯 新,翁艺航,熊一帆,景 飞
(1.上海交通大学机械系统与振动国家重点实验室,上海 200240;2.上海航天电子技术研究所,上海 201109)
0 引言
在现代工业中,滑环大量应用于需要连续回转且需要在固定端和旋转端之间传输电能和信号的机械关节与机电系统,尤其常见于传统发电设备、航天飞行器、各种工业与医疗机器人中[1-2],其能够避免线缆拉扯扭伤等情况,简化机电系统结构,提高系统传输性能和可靠性。
目前,在上述领域常用的接触式滑环具备着体积小、能量密度高的优势。但同时,其采用了电刷结构传输电能与信号,由于机械结构与传输方式限制,接触式滑环也会带来摩擦磨损,产生导电碎屑甚至出现电火花和击穿等问题[3-4]。为克服接触式滑环的上述缺陷,完成连续旋转关节上的电能与信号传输,针对非接触式滑环的研究开始受到重视。文献[5]介绍了一种经过优化的应用于旋转超声加工领域的滑环结构,其具有传输效率高、输出能力强和安全性能良好的特点;文献[6]提出了一种新的滑环结构,相比传统的滑环结构提高了功率传输能力和效率,并通过有限元分析和比较实验证实该新型结构相较于传统滑环结构有更优的表现。
热失效是滑环的一类重要失效模式,对滑环的稳定性、可靠性和寿命有很大的影响。非接触式滑环的热效应主要由功率传输中的磁芯损耗、传输电流焦耳热和零件涡流效应等产生,而应用于航空航天、水下作业和半导体工业等领域的滑环工作在真空环境下,缺乏有效对流换热手段,散热条件苛刻,热失效的可能性和危害大大提升[7]。
本文根据非接触式滑环功率传输部分的热效应,通过对具有冗余备份的非接触式功率传输滑环装置进行机械结构设计、热学模型建立、相应热源分析及热仿真,获得其稳态下的热性能、温度分布图与热通量图,验证非接触式滑环设计的合理性;并分析热设计的薄弱环节,指导后续的散热设计。
1 非接触式滑环机械结构设计
非接触式滑环的机械结构设计主要涉及功率传输部分设计、冗余设计及其总体装配结构设计等。
在功率传输部分的设计中,存在平面型和共轴型2种结构[8]。功率传输部分的磁芯,在平面型结构中呈上下相对放置,气隙在中央呈平面型;在共轴型结构中呈内外相对放置,气隙在中央呈圆柱形。平面型和共轴型磁芯结构设计剖视图如图1所示。
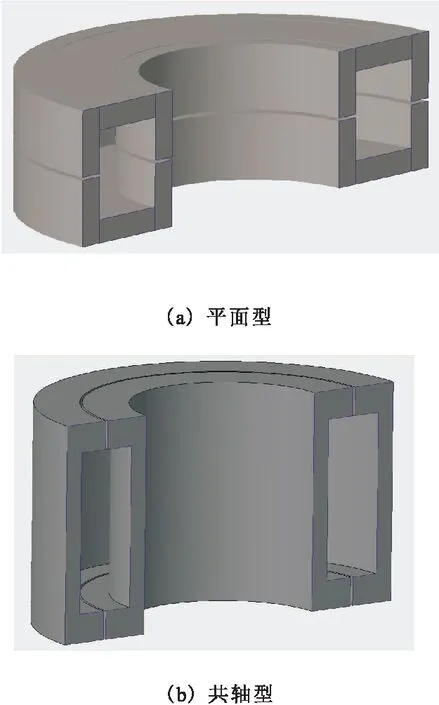
图1 磁芯结构设计模型剖视图
为达到目标的传输效果,磁芯结构需要正向相对、尽量减小偏移,保证平行度或同轴度良好,因此平面型对装配精度要求很高;而共轴型结构的内外壳体分别可以做成一体设计,能够保证换热面充足,方便后续设计中热量从散热结构导出,在热分析下有更好的表现。出于对加工、装配难度和散热条件等的综合考虑,将功率传输部分设计为共轴型,将冗余构型设计为上下型,整体结构剖视图如图2所示,上半部分结构为非接触式滑环的有效载荷。

图2 滑环装置设计模型剖视图
2 非接触式滑环热学模型分析
非接触式滑环的主要热源包括以下几方面:功率传输中交变磁场引起的磁芯损耗、功率传输或信号传输中电流的焦耳热效应和滑环工作时轴承产生的摩擦热等。对非接触式滑环中的温度分布定性或简单的定量分析时,可以通过热分析模型进行大致推导[9]。根据装配关系,线圈与磁芯接触,磁芯和轴承分别与壳体接触,可以得到滑环的热分析模型如图3所示,其中,c1、c2、b、s、a分别为线圈、磁芯、轴承、壳体、环境,角标′表示冗余。

图3 非接触式滑环热分析模型
参照电路模型分析原理分析该模型[10]。当部件体积较小或者为金属件、有较大的导热系数和热扩散系数时,近似认为同一部件中的温度均一,从而可应用上述热分析模型进行分析。根据该模型,可以得到以线圈焦耳热、 磁芯损耗发热和轴承摩擦热为热源,非接触式滑环达到稳态热平衡时,线圈、磁芯、轴承和壳体等各部件相对于环境的温升。主体部分各个部件的温升如式(1)~式(4),其中,θ为部件温度;P为热源热流;R为部件间的热阻。
Δθc1a=θc1-θa=Pc1Rc1c2+(Pc1+Pc2)Rc2s+
(1)
Δθc2a=θc2-θa=(Pc1+Pc2)Rc2s+
(2)
Δθba=θb-θa=
(3)
(4)
非接触式滑环工作环境为真空,因此没有对流换热,式(1)~式(4)中的热阻项仅由直接接触传热热阻和热辐射等效热阻并联构成。其中,线圈与磁芯、磁芯与壳体、轴承与壳体为直接接触,可认为接触热阻占相应热阻项的主要部分,如式(5)~式(7);壳体与环境主要通过辐射换热,对应热阻项如式(8)。
Rc1c2=Rcond,c1c2∥Rrad,c1c2
(5)
Rc2s=Rcond,c2s∥Rrad,c2s
(6)
Rbs=Rcond,bs∥Rrad,bs
(7)
Rsa=Rrad,sa
(8)
各部件的热容由部件材料的比热容与质量决定;接触热阻由接触表面的压力、光滑程度和接触面间的介质属性决定。实际非接触式滑环中,由于加工装配精度的限制和表面粗糙度的存在,接触表面间的传热需要通过接触间隙的传导和辐射实现,因此存在一定的接触热阻和温降。实际情况将比上述热模型更加复杂。
3 非接触式滑环热源分析
非接触式滑环产热的热源主要来自以下几方面:功率传输部分中的磁芯损耗(铁损)、线圈损耗(铜损)以及滑环工作时轴承产生的摩擦热等。
3.1 磁芯损耗(铁损)分析
非接触式滑环的功率传输部分工作原理与变压器类似,通过原边、副边2组线圈和磁芯共同形成电磁耦合,在原边线圈中通入交变电流,并借助磁芯约束磁场形成磁路,从而在副边线圈中感应出交变电流,完成功率传输。在该过程中,交变磁场作用在磁芯上,将产生磁芯损耗。
磁芯损耗主要分为磁滞损耗、涡流损耗和剩余损耗,但多数情况以磁芯损耗和涡流损耗为主。
磁滞损耗(Ph)来自于铁磁材料在交变磁场被反复磁化的过程中因磁滞现象消耗的能量。在铁磁材料磁化过程中,铁磁材料中的磁感应强度B相较于外界磁场强度H的变化有一定滞后,相应地,有一部分磁场能量用于克服铁磁材料中原先磁化保留下来的磁场,因而不可逆转地转化为热能并耗散。
涡流损耗(Pe)则是因为许多磁芯材料本身就有一定导电性,因此在交流磁场下工作时,磁芯中将产生呈涡流状的闭合的电流,这部分电流在磁芯上产生的焦耳热形成了涡流损耗。
剩余损耗(Pc)是由于铁磁材料的磁化弛豫效应或磁性滞后效应引起的损耗。外部磁场变化后,铁磁材料的磁化状态并不马上跟随外部磁场发生改变,而是存在一个弛豫时间,从而引起剩余损耗。
传统的磁芯损耗理论公式采用损耗分离法,将磁芯损耗分成上述3类损耗计算。单位体积的磁芯损耗理论公式如式(9)~式(10),其中,Kh、Ke、Kc分别为磁滞损耗、涡流损耗、剩余损耗系数项;f为交变磁场的频率;Bm为磁芯中磁感应强度的峰值。
Pv=Ph+Pe+Pc
(9)

(10)
在非接触式滑环中,磁芯材料选择铁氧体PC40,根据磁芯厂家提供的P(磁芯损耗)-B(磁感应强度)曲线簇,可以通过最小化平方差拟合得到系数Kh、Ke、Kc,如式(11),其中,m、ni分别为曲线簇中P-B曲线数量和每条P-B曲线上的数据点数。拟合得到的Kh、Ke、Kc如表1所示。
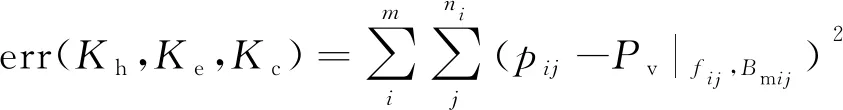
(11)
为获得磁感应强度峰值Bm,并对磁芯损耗进行更精确的估计,对比其理论计算和仿真数值,采用电磁仿真软件Maxwell,对功率传输部分的线圈-磁芯结构分别进行2D稳态涡流场仿真和瞬态场仿真。
稳态涡流场仿真中,对线圈通以频率为20 kHz、有效值为10 A、相位差为180°的正弦波交变电流,设定相应磁芯材料损耗参数和线圈材料后,得到磁芯上的磁感应强度幅值仿真结果如图4所示。忽略磁芯结构突变处的无效尖峰值,以磁芯中间部分最大磁感应强度为准,则在功率传输结构中,内圈磁芯磁感应强度峰值为0.070 4 T,外圈磁芯磁感应强度峰值为0.044 3 T,低于所选用PC40磁芯材料的饱和磁感应强度Bs,经验证是安全的,并将该数值作为内外圈磁芯损耗理论计算的依据之一。

图4 磁芯磁感应强度仿真结果
瞬态场仿真中,对线圈的激励电流在仿真时间起点施加1个衰减项,保证系统较为平稳地到达稳态以获得可靠的仿真结果。仿真得到前500 μs内,整个功率传输结构的磁芯损耗、涡流损耗、磁滞损耗如图5a所示,内外圈磁芯各自的磁芯损耗如图5b所示,并对稳定后的损耗曲线求平均值得到表2所示。

表2 磁芯损耗平均数值

图5 磁芯涡流损耗仿真曲线
同时,根据式(9)、式(10)和图4对磁芯磁感应强度的仿真结果,可以得到内外圈磁芯损耗的理论计算数值,其与仿真结果对比如表3所示。

表3 磁芯损耗理论计算与仿真对比
总体上,磁芯损耗的理论计算数值与仿真结果误差较小,相比之下内外圈磁芯损耗理论计算数值与仿真结果误差稍大,原因或在于仿真模型不够精细、磁场磁感应强度结果划分较为粗糙、磁芯损耗理论公式存在一定的误差需要修正等。后续以仿真结果数值作为热分析模型的内热源激励之一。
3.2 线圈损耗(铜损)分析
线圈损耗即为功率传输部分的导线存在一定电阻,当导线上有电流时,会产生相应的焦耳热效应,可以通过导线电阻和工作电流进行计算。导线电阻与导线电阻率、导线长度和横截面积有关,如式(12)所示,非接触式滑环中线圈选用640股0.1 mm的利兹线,横截面积为5.026 5×10-6m2,内外圈线圈长度分别为4.684 m、6.098 m,铜的电阻率ρ取1.75×10-8Ω·m;线圈损耗计算如式(13)所示,电流有效值取10 A。计算可得内外圈线圈电阻分别为0.016 3 Ω、0.021 2 Ω,对应的线圈损耗项分别为1.630 8 W、2.123 0 W。

(12)
PI=I2R
(13)
3.3 轴承发热分析
轴承发热主要来自于轴承工作时的摩擦产热,其可以通过轴承载荷和轴承参数进行计算[11]。轴承摩擦力矩估算公式如式(14)所示,其中,所选用深沟球轴承摩擦系数μ取0.002,轴承载荷F按整个非接触式滑环自重估计为278.42 N,轴承内径d单位为mm,轴承摩擦力矩M单位为N·mm。

(14)
轴承摩擦产热发热量计算公式如式(15)所示。其中,轴承转速n取冗余滑环的工作转速36 r/min,轴承发热功率Q单位为W。计算可得上下2个轴承的摩擦产热分别为0.105 2 W、0.084 2 W。
Q=1.05×10-4M·n
(15)
4 非接触式滑环热仿真
在非接触式滑环实际工作环境中,有多种热源分布在多个部件上,部件之间的热传导、热辐射等也与机械结构、接触条件等紧密相关,同一部件上的温度分布也并不均匀。为更精确地获得非接触式滑环的热性能,验证非接触式滑环的设计,并分析非接触式滑环中热设计的薄弱环节,基于上述对非接触式滑环热模型、热条件及热源等相应理论分析,使用ANSYS有限元分析软件对非接触式滑环进行进一步热仿真分析。
在非接触式滑环热仿真模型中,壳体材料设置为铝合金7075,磁芯材料设置为PC40铁氧体,线圈材料设置为铜,轴承材料设置为结构钢。
根据上述非接触式滑环热源分析进行热源设置。在非接触式滑环中,功率传输部分具有冗余备份设计,包含2组线圈-磁芯结构,冗余部分和主体部分是否同时工作与冗余策略有关。为验证更广泛、更极端的工作情况,仿真中设置2组线圈-磁芯结构同时发热。分别对磁芯损耗热源、线圈损耗热源和轴承摩擦热源进行计算,并设置相应的单位体积产热量。
非接触式滑环的散热换热方式根据实际工作环境设置。零件间的热传递为接触面间含间隙热阻的热传导;壳体向工作环境温度50 ℃辐射换热;在所有大空腔结构内部设置面对面热辐射条件。
通过上述热仿真条件分析,设置相应的仿真参数如表4所示,得到非接触式滑环在频率20 kHz、有效值10 A的交变电流激励下的稳态温度分布如图6所示,稳态总热通量分布如图7所示。

表4 非接触式滑环热仿真模型参数

图6 稳态温度分布

图7 稳态总热通量
根据图6稳态温度分布的仿真结果,非接触式滑环达到稳态工作时最高温度为82.010 ℃,集中出现在线圈处;最低温度为63.709 ℃,在外圈壳体上。虽然温升在各部件材料温度耐受范围内,表明非接触式滑环设计的合理性,但仿真的结果较为理想化,仍应考虑散热设计的实际需要,降低非稳态条件、极端环境温度等恶劣工作条件可能带来的影响。
根据图6的温度分布结果,壳体、磁芯和轴承的温度分布较为均匀且温升相对较低,温升主要集中在线圈处,这表明线圈需要效果更好的散热设计。线圈主要与磁芯接触和辐射换热,可考虑在线圈与磁芯之间的间隙涂抹导热系数高的材料,使线圈的热量通过磁芯逸散。在2部分壳体中,内轴的温升较外壳高6~8 ℃,这与内轴孔径小、与环境辐射换热更为困难的情况一致,如需对壳体进行加强散热设计,应首先考虑将热量从内轴导出。
根据图7稳态热通量的仿真结果,部分热通量最大值出现在内轴壳体中部、轴承和线圈上,同时外圈壳体中部也有较大的热通量。因此,如需对壳体加强散热,应重点考虑这些热通量和温度均较高的位置。而轴承和线圈的热通量峰值是由于热源大而接触面积小产生的,难以优化,参考意义不大。
5 结束语
本文根据非接触式功率传输要求,针对具有冗余备份的非接触式功率传输滑环,完成了其功率传输部分机械结构设计,随后建立了相应的热学理论模型,并对各部件的温升、热阻和热源进行分析。对非接触式滑环的磁芯损耗、线圈损耗和轴承摩擦损耗3类损耗热源进行定量分析,其中对磁芯损耗进行电磁场仿真,获得了磁芯上的磁感应强度,据此计算磁芯损耗的理论值并与瞬态场仿真结果对比。基于损耗分析进行非接触式滑环的热仿真,仿真表明装置总体温升在允许范围内,验证了非接触式滑环设计的合理性,并指出后续应着重考虑线圈和内轴壳体中部的散热设计。在今后的工作中,将进一步完善细化热学理论模型和热仿真,并对非接触式滑环进行实验以获得实际温升情况。

