采用压-拉杆模型计算型钢混凝土深梁承载力

卢化松

（基准方中建筑设计股份有限公司，成都 610011）

1 引言

深梁是指跨度与其高度之比较小的梁。我国GB 50010—2010《混凝土结构设计规范》[1]（2015年版）（以下简称《结构规范》）规定，跨高比l0/h＜2的简支梁或l0/h＜2.5的连续梁属于深梁。型钢混凝土（SRC）深梁由于其承载力高等优点，已广泛应用于高架车站、住宅转换中。

SRC深梁因其跨高比较小，受外力作用时，内部受力较复杂：存在受压、受弯及受剪状态，平截面假定不再适用，经典的梁理论设计方法已不适宜，而压-拉杆模型提供了解决方案。

压-拉杆模型起源于桁架模型，它将钢筋混凝土构件简化为混凝土压杆、钢筋拉杆以及节点区。压-拉杆模型能有效反映构件的传力机制，设计过程简单。在国内，叶列平[2]、贡金鑫[3]等对压-拉杆模型的应用进行了研究，取得了较好的效果。

根据圣维南原理，压-拉杆模型将构件分为B区和D区，B区为应力线性分布，满足平截面假定；D区较高的剪应力使截面发生明显翘曲，平截面假定不再适用。在梁的正截面受弯及斜截面受剪设计时，对于B区，我国规范采用极限状态法进行承载力的计算，理论较为成熟；对于D区，通常采用经验计算或局部加强构造措施，缺乏理论指导。压-拉杆模型可真实反映D区的荷载传递机制，是D区截面设计的一种简便的方法。

本文采用荷载路径法，确定SRC深梁的压杆、拉杆及节点区强度，合理考虑型钢在压-拉杆中的强度，建立节点平衡方程。通过分析SRC深梁的破坏模式，得出SRC深梁的实际承载力。

2 SRC深梁压-拉杆模型

在竖向荷载作用下，SRC深梁受力模式分析可简化为压-拉杆模型，即将受拉开裂的混凝土和型钢受压部分等效为压杆，将受拉纵筋和型钢受拉翼缘等效为拉杆，将压-拉杆的交汇区域看成节点。根据荷载分布情况，由结构力学方法可以求出拉杆、压杆、节点的内力，并应满足式（1）要求：

式中，N为拉杆、压杆和节点的轴力；Nu为拉杆、压杆和节点的轴向承载力。

压-拉杆模型较合理地反映了混凝土深梁的受力状况，满足塑性下限定理。因此，结构实际承载力大于按压-拉杆模型所预测的承载能力，简化模型是安全可行的。建立压-拉杆模型应依据结构的应力分布图，目前主要有：应力迹线法、有限元法等[4]。本文对拉杆、压杆、节点区进行分析。

2.1 拉杆

拉杆由纵向受拉钢筋和型钢受拉翼缘及其周围同轴线的混凝土组成。拉杆承载力Ntu按式（2）计算：

式中，fy、fa分别为钢筋、型钢的屈服强度；Ast、Aa分别为受拉钢筋、型钢受拉翼缘的面积。

2.2 压杆

压杆代表模型中压力场的合力，根据压力扩散情况，可以分为棱柱形、瓶形和扇形，如图1所示。一些学者建议水平压杆使用棱柱形、斜压杆使用瓶形，如图2所示，图2中P为梁承担的集中荷载。本文采用上述学者的建议，根据《结构规范》并参考ACI规范[5]，建立钢筋混凝土受压杆件的计算公式。

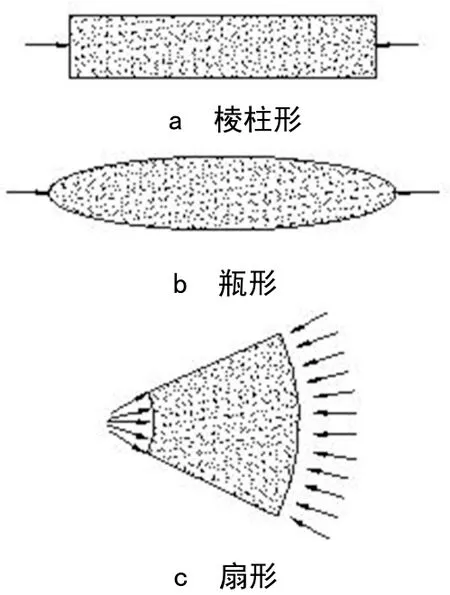
图1 压杆的类型

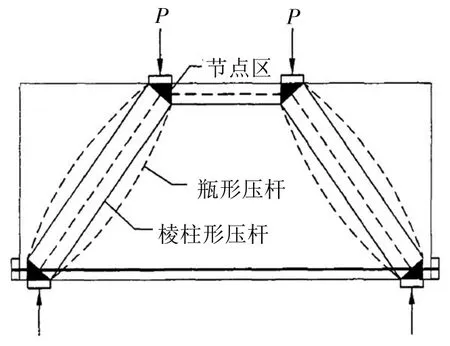
图2 压-拉杆模型

水平压杆承载力Ncu按式（3）计算：

斜压杆承载力Ncu按式（4）计算：

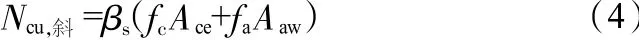
式中，fc为压杆混凝土抗压强度；Ace、Aa、Aaw、As分别为压杆端的混凝土截面面积、型钢受压翼缘面积、斜压杆型钢受压腹板面积、受压钢筋面积；βs为压杆有效抗压强度影响系数，按表1取值。

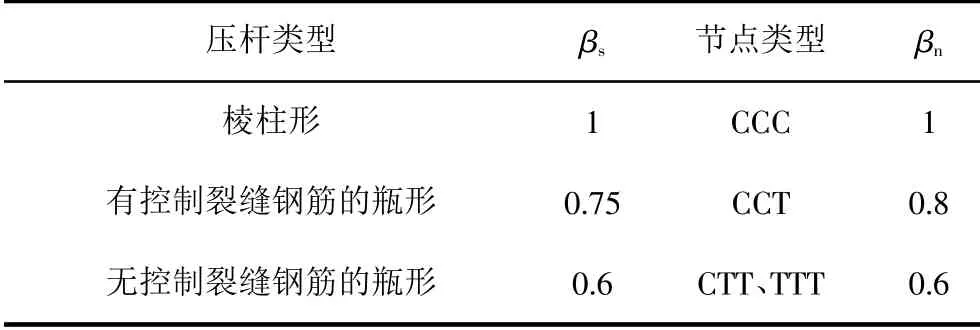
表1 βs、βn的取值

由于深梁中的假想压杆受周围介质的约束，一般不会失稳，故式（3）和式（4）未考虑稳定系数。另外，《结构规范》公式为了统一可靠度，对式（3）和式（4）的右端项乘以系数0.9，这在压-拉杆模型中可不考虑。

为控制裂缝，压杆横截面配筋应满足式（5）：

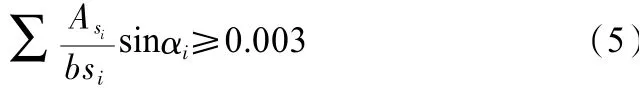
式中，αi为压杆轴线与钢筋轴线的夹角；Asi为与压杆方向成α角度的钢筋层中，间距si钢筋的总面积，见图3；b为深梁截面宽度。

图3 与压杆相交的钢筋

2.3 节点区

为了满足压-拉杆模型的受力平衡，节点区的受力状态可简化为3个集中作用力。根据受力状态的不同，节点区可分为3个压力节点(CCC)、两个压力和一个拉力节点（CCT）、一个压力和两个拉力节点（CTT）、3个拉力节点（TTT），如图4所示。对于不同的节点类型，节点区的容许压力Nnu按式（6）计算：

图4 节点类型

式中，Aaw为节点区的斜压杆型钢腹板有效受压面积，对水平杆件可取为0；βn为不同类型节点对应的强度折减系数，其取值如表1所示[2]。

2.4 SRC深梁压-拉杆模型的建立

对于任意一个SRC简支深梁，在对称荷载作用下，简化的压-拉杆模型如图5所示，虚线表示压杆、实线表示拉杆。压-拉杆组成的模型是机构的，在A、D之间布置杆件，构成稳定体系。

图5 对称荷载下的拉压杆模型

对深梁梁端支座处的垫板，参考《结构规范》中局部受压承载力计算公式，其长度xR可近似按式（7）确定：

式中，F/2为支座集中反力；βc为混凝土强度影响系数，C50及以下取1.0，C80及以上取0.75，中间强度按插值法计算；βl为局部受压面积比，支座处取1.0。

AB拉杆和CD压杆的承载力分别按式（8）和式（9）计算：

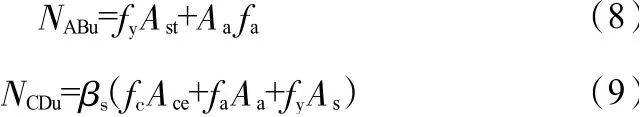
AB拉杆和CD压杆的节点区应分别满足：

式中，xt、xc分别为水平拉杆、压杆的等效宽度；βnAB、βnCD分别为AB杆、CD杆对应的强度折减系数。

假设受拉钢筋和受拉型钢屈服，则由式（8）和式（10）可得：

分析表明，AD杆件内力为零，故有FAB=FCD。假设CD杆和AB杆在节点区均达到相应的承载力，即：

由表1可知：CCC型节点；CCT型节点，故有：

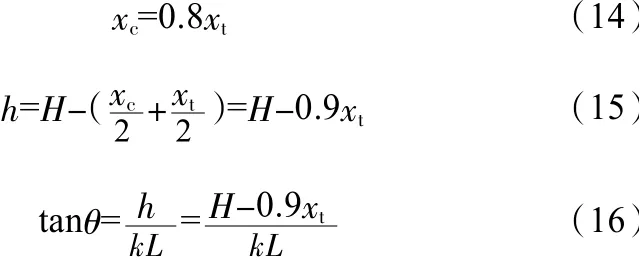
式中，H为深梁的高度；h为上下拉、压杆中心线之间的距离；kL为集中力到支座处的水平距离；θ为斜压杆与水平拉杆间的夹角。

2.5 模型分析

支座处受力状况（CCT节点）如图6所示。

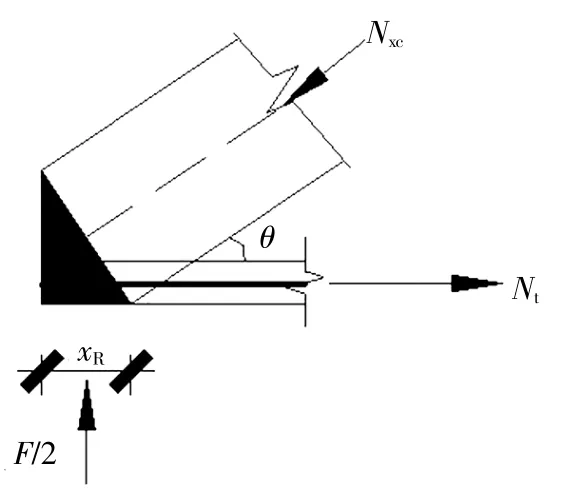
图6 支座处受力状况

斜压杆有效宽度xs为：

斜压杆承载力Nxc满足：

式中，Aaxc为Nxc方向的型钢腹板截面面积。

将式（2）和式（18）代入式（19），得：

式中，tw为型钢腹板厚度。

如果实际配置纵筋Ast,a≥Ast，可以判定构件主要发生剪切破坏；如果实际配置纵筋Ast,a＜Ast，可以判定构件主要发生弯曲破坏。

2.6 承载力分析

2.6.1 弯曲破坏

当时，受拉钢筋和型钢受拉翼缘达到屈服状态，按下式确定，即：

则深梁弯曲破坏时的承载力Fu计算如下：

2.6.2 剪切破坏

当Ast,a≥Ast，即受拉钢筋未屈服时，取xt=2αs(αs为拉杆中心线到构件受拉边缘的距离)，由节点平衡条件可得：

将式（7）和式（17）代入式（24），得：

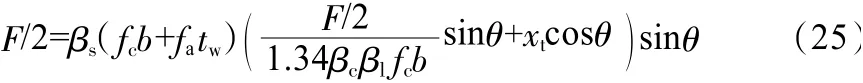
即：

对于瓶形斜压杆，βs=0.75，代入式（26），得：

3 试验结果对比分析

本文共搜集了25个SRC深梁的试验数据，均为集中荷载作用：其中4个为弯曲破坏，21个为受剪破坏[6-8]。分别采用YB 9082—2006《钢骨混凝土结构技术规程》[6]（以下简称《钢骨规程》）和本文提出的拉压杆模型公式计算承载力，并与试验结果进行对比分析，结果如表2所示。

表2 承载力验算

上述对比结果表明，《钢骨规程》关于SRC深梁的计算公式偏于保守，变异系数也较大；而本文提出的压-拉杆模型计算公式能较好地反映SRC深梁的极限承载力，变异系数也较小。

4 结论

我国《钢骨规程》没有明确的SRC深梁计算公式，而是统一采用平截面假定，采用一般SRC梁的计算公式。正截面和斜截面承载力设计，均是根据试验回归统计而来，缺少理论模型的支持。

压-拉杆模型满足塑性下限定理，是安全可靠的。根据收集到的试验数据计算分析，采用本文提出的压-拉杆模型的计算值与试验值吻合较好，且离散性相对较小；《钢骨规程》计算值比试验值偏低较大，且离散性较大。

本文提出的压-拉杆模型计算过程简单，其将受力复杂的SRC深梁等效成杆系结构，以杆系结构的受力机制代替SRC深梁实体的受力机制，能较好地反映SRC深梁的受力机制。