“胶囊形”钢管混凝土柱受弯承载力方法
郭振勇,刘开康,傅慧敏,马瑜杰
(1.中铁工程设计咨询集团有限公司,北京 100055;2.中国中元国际工程有限公司,北京 100089)
1 引言
圆钢管混凝土柱因为轻质高强度的优势,现在被广泛应用于高速铁路建设中(特别是高铁站房及无站台柱雨棚)。但是部分跨线站房由于高铁线间距的限制,圆钢管混凝土柱直径有限,无法采用,而方钢管混凝土柱尽管抗弯线刚度相对较大但不满足建筑美学要求。基于此,本文提出“胶囊形”钢管混凝土柱,兼具圆钢管混凝土柱线条优美和方钢管混凝土柱承载力的优点,但该类型柱无相关规范可以采用[1-2]。本文根据钢管混凝土构件受弯极限状态时的承载力特征,推导出了“胶囊形”钢管混凝土柱受弯承载力计算公式。
2 基本假定
钢管混凝土的本构关系非常复杂,若直接应用将很难得到承载力的解析表达式,可以忽视钢管和混凝土之间的黏结作用,故在分析计算时,做出如下假设:
1)钢管和混凝土之间无相对滑移发生,为完全黏结;
2)在极限状态下,钢管受拉部分和受压部分同时达到屈服,屈服应力的大小相同;
3)不考虑钢管约束对受压区混凝土强度的提高,取混凝土抗压强度σc=fc(fc为混凝土轴心抗压强度),并且由于受拉区混凝土对抗弯的贡献较小,故假定受拉区混凝土不参与工作;
4)构造保证钢管不发生局部屈曲,钢管形状和面积屈服前后保持不变[3]。
3 抗弯承载力计算公式推导
根据上述假设,在极限状态时,“胶囊形”钢管混凝土柱截面的受力情况如图1和图2所示。
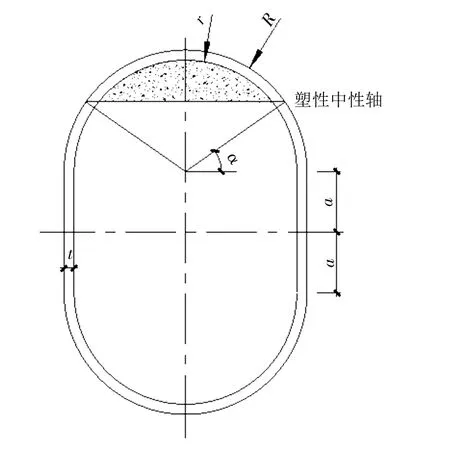
图1 塑性中性轴位于半圆范围内示意

图2 塑性中性轴位于半圆范围外示意
3.1 计算塑性中性轴位置
受拉区钢管所受的拉力Nst以及受压区混凝土所受的压力Ncc分别为:

式中,f为钢抗弯强度设计值。
若Ncc≥Nst,则塑性中性轴在半圆范围内;若Ncc<Nst,则塑性中性轴在半圆范围外。
3.2 若塑性中性轴在半圆范围内
假设受压区对应弧度为α,受拉区钢管所受拉力Nst、受压区钢管所受压力Nsc和受压区混凝土所受压力Ncc为:

由Nst=Nsc+Ncc,可得出:


用迭代可求出α=α0。
可得出钢管部分承担的弯矩为:

式中,rm为钢管壁中心到圆心的距离,即rm=(R+r)/2。
混凝土部分承担的弯矩为:

“胶囊形”钢管混凝土柱受弯承载力:
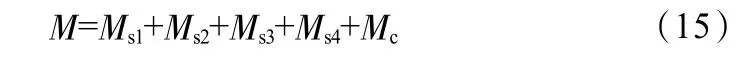
3.3 若中性轴在半圆范围外
假设受压区边缘与中性轴距离为x,受拉区钢管所受拉力Nst、受压区钢管所受压力Nsc、受压区混凝土所受压力Ncc为:

令Nst=Ncc,则:



混凝土部分承担的弯矩Mc为:
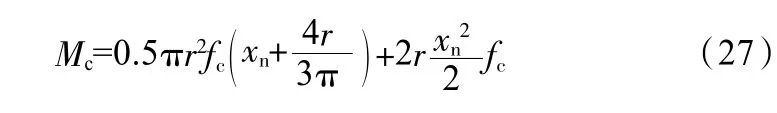
“胶囊形”钢管混凝土柱受弯承载力M=Ms1+Ms2+Ms3+Ms4+Mc。
4 结论
本文通过分析受弯极限状态下“胶囊形”钢管混凝土柱构件的截面受力特性,推导出内力平衡方程,从理论上推导出比较准确的“胶囊形”钢管混凝土构件抗弯承载力公式,以便于实际设计中使用,并可参照推导出其他各类特殊的钢管混凝土构件的抗弯承载力公式。

