一种天地一体化智能网络流量模型
杨 力,庞 涛,孔志翔,魏德宾,
1(大连大学 通信与网络重点实验室,辽宁 大连 116622)
2(大连大学 信息工程学院,辽宁 大连 116622)
3(南京理工大学 自动化学院, 南京 210094)
E-mail:974497800@qq.com
1 引 言
天地一体化网络是以传统卫星网络为基础,为天基组网,地网跨代,天地互联,为天陆空等各类用户提供了可靠的基础设施[1].天地一体化网络能够实现全球覆盖,随处接入,按需服务,安全可信的网络连通[2],进而对网络中节点的存储、计算和通信转发能力的要求逐步增加,最终向天地一体化智能网络方向发展.
天地一体化智能网络规模庞大,网络环境复杂多变,具有高度的动态性、复杂性和不确定性.智能节点具备了存储和计算能力,用户可以从缓存节点直接获取请求信息,加快内容分发的速度,内置缓存功能可以减少流量交换,大数据变成小数据,网络流量特征会发生变化[3].流量模型能够精确刻画实际网络流量特征,通过建立网络流量模型指导天地一体化智能网络设计,对网络性能分析、参数设计和拥塞控制有着重要意义[4].
2 相关工作
网络流量模型主要分为以下3种:传统网络流量模型、自相似网络流量模型和混合流量模型.网络流量在大时间尺度下的自相似性和小时间尺度下的多分形性是重要的且公认的统计特征.以上特性也存在卫星网络中[5].
文献[6]和文献[7]研究地面网络流量在通过地面网关进入卫星网络后流量的根本特性(自相似、长相关、突发性等)不会发生改变,但会增加流量叠加到卫星后的时变性、非线性的复杂度.文献[8]采取扩散小波技术对网络流量矩阵进行了多尺度分析,选取了特征参数对原始流量进行特征分析.文献[9]对网络流量的四种状态进行分析研究得出,IP网络流量在忙状态和空闲状态分别服从几何布朗运动和正太分布,符合上升或下降状态的指数分布.文献[10]研究表明传统的多重分形时间维分析方法不能确定自相似性和多重分形变换在什么尺度上发生,从而不能确定多重分形的成因.流量在时间尺度较小时更趋于多重分形.文献[11]中分形布朗运动被替换为多分形布朗运动,升级了分形布朗运动.扩展的多分形布朗模型可以匹配小时间尺度下流量的多重分形和大时间尺度下流量的长相关性.但是不能准确描述多重分形谱.文献[12]通过研究分析树型多重分形结构,多重分形通过用短相关(SRD)模型表示的序列组代替具有长相关和分形特征的非平稳网络流量序列.采用多重分形的方式把时间序列分解为多层,构建了一种FIR神经网络与多重分形相结合的流模型.文献[13]利用信息熵的方法,发现流空间中的信息单元存在着远距离的互相关性.但是这些模型与适应突发性不强的地面网络流量描述有关,不符合天地一体化智能网络流量描述.
天地一体化智能网络在多速率异构链路汇聚条件下,流量急速增长,智能网络流量表现为突发性增强,传统流量模型在网络流量突发性增强的条件下无法描述流量特性,突发性通常由节点流速的分布特性决定,威布尔分布生成的随机数实例表现出明显的高突发性.为此,文章提出了一种基于威布尔分布的混合小波网络流量模型.该模型结合IWM的长相关描述能力以及MWM的短期突发的描述能力,通过设定随机乘法系数来确保流量非负,进而确保重构智能网络流量为正,确保流量的真实特性,选取Weibull分布重构符合智能网络突发性强的流量信号,该模型能够精确描述天地一体化智能网络流量特征,性能表现更优.
3 流量特性与模型分析
3.1 重尾分布的网络流量
W.Willinge[14]等人认为通过重尾分布来描述复杂的网络流量的分布特征.
Weibull分布[15]作为经典的重尾分布,概率密度函数表示如下:
f(t;λ,k)=kλtλk-1e-(t/λ)kt≥0
0t<0
(1)
其中,k是形状参数,代表重尾程度,λ是分布的比例参数.只有当威布尔分布的形状参数c的值小于1时,它才是重尾的.
Weibull分布生成的随机数实例突发性表现强烈,天地一体化智能网络流量具有强烈的局部突发性,通过Weibull分布来重构具有的突发性强的智能网络流量的随机过程,能够精确描述天地一体化智能网络流量特性.
3.2 流量特性分析
地面网络流量在通过地面网关进入天地一体化网络后,流量的自相似性不会发生改变,流量具有明显的尺度特性[16].对于不同尺度下的流量特征参数,表现为互相关联.当网络流量汇聚时,流量的强突发性通过不同尺度观测到,相关性用长相关来刻画[17].在刻画实际环境中的流量特性时,对于仅用一个参数(Hurst parameter)的自相似性模型明显不适用于天地一体化智能网络流量分析.随着天地一体化智能网络业务的开展,天地一体化智能网络流量在链路汇聚时突发性增强[18].随着时间尺度的增加,真实流量的突发性不会趋于平滑.本文的模型通过选取符合流量突发性的威布尔分布合成流量,在大小时间尺度上都能明显的反映流量突发性.模型能够很好的刻画流量特性.
3.3 独立小波模型和多重分形小波模型分析
独立小波模型(IWM)的最粗尺度系数U0,0和小波系数Wj,k均采用递归的方式计算,得到精细部分的尺度函数Uj,k.通过计算得到了所有尺度j下的尺度系数Uj,k,然后对信号Xiwm(k)进行重构.IWM能够准确流量的长相关过程,但是在重构流量信号时存在负值.
多重分形小波模型(MWM)在小波逆变换迭代过程为了确保最粗尺度系数U0,0>0,并且满足|wj,k| Wj,k=Aj,k×Uj,k (2) 其中,Aj,k是取值[-1,1]在上的独立随机变量,确保在迭代过程中每个尺度系数为正. MWM具体算法描述如下: 1)j=0,由β分布在区间[0,1]计算得到最粗尺度系数U0,0; 2)尺度j下,随机乘法因子Aj,k由β分布产生,公式Wj,k=Aj,k×Uj,k计算Wj,k,k=0,1,…,2j-1; 3)在尺度j上,小波逆变换通过用Uj,k和Wj,k计算出尺度j+1的Uj+1,2k和Uj+1,2k+1,k=0,1,…,2j-1; 4)增加j,重复步骤2,步骤3,求得最细尺度j=n下2n个尺度系数Uj,k为止. 该模型能够描述流量多重分形和短期突发性,缺点是不能保证小波变换系数在每个尺度下都独立. 传统多分形小波模型构造系数的分布选取与实际流量分布特性无关,而天地一体化智能网络流量具有长相关和突发性强的特点,导致传统多分形小波模型无法适用于天地一体化智能网络,本文通过对多分形小波模型构造系数分布合理化选取,构建了基于威布尔分布的混合小波网络流量模型,该模型能够很好的模拟智能网络流量生成,并且能够准确、有效的描述天地一体化智能网络流量的行为特征. 基于威布尔分布的混合小波网络流量模型需要完成以下几点: 1)尺度系数Uj,k通过IWM来确定,随机系数因子Aj,k用MWM来确保流量非负,确保网络流量的真实特性. 2)不在选用和实际流量无关的β分布确定最粗尺度系数U0,0和随机系数因子Aj,k,选取具有描述突发性强的Weibull分布,该分布能够准确模拟智能网络流量的突发性强特性. W_OWM通过IWM算法确定尺度系数Uiwmj,k,设定随机乘法因子Aj,k,为了使信号非负,限制条件|Wmwmj,k|≤Umwmj,k: Ww_owmj,k=Aj,kUiwmj,k (3) 可以得出W_OWM小波系数Ww_owmj,k,通过计算得到的尺度系数Uiwmj,k和小波系数Ww_owmj,k使用迭代公式(4). Uw_owmj+1,2k=2(-1/2)*(Uiwmj,k+Ww_owmj,k) (4) 计算W_OWM尺度系数Uw_owmj+1,k,将式(3)代入式(4),迭代公式简化为: Uw_owmj+1,2k=2(-1/2)(1+Aj,k)*Uiwmj,k (5) IWM不能保证尺度系数Uiwmj,k非负,通过公式(5)发现,为了确保下一尺度系数Uw_owmj+1,k非负,对正负尺度系数分别进行不同处理.天地一体化智能网络流量具有明显的长相关特性,IWM能够描述流量的长相关过程,该模型结合IWM模型的优点,使用IWM产生下一尺度系数能够更好的描述天地一体化智能网络流量的长相关特性. 若Uiwmj,k≥0,为了确保尺度系数为正,根据迭代公式(4)来满足限定条件|Ww_owmj,k|≤Uiwmj,k,进而引入随机乘法因子Aj,k设定在区间[-1,1]上. 若Uiwmj,k<0,通过简单移位处理乘法因子Aj,k来确保下一尺度系数(公式(5)计算出)为正. W_OWM算法具体描述如下: Step 1.最粗尺度系数Uw_owm0,0由Weibull分布产生. Step 2.尺度系数Uiwmj,k通过IWM模型算法计算. Step 2.1.通过指定高斯分布来计算尺度j-1小波系数为Wiwmj-1,k∈N(0,σ2j-1),其中,σ2j-1为小波系数方差. Step 2.2.尺度系数Uj,k通过已经计算出的尺度系数Uj-1,k和小波系数Wj-1,k运用迭代公式计算. Step 3.判断Uiwmj,k Step 3.1.当Uiwmj,k≥0 Ⅰ)若|Wiwmj,k|≤Uiwmj,k Ww_owmj,k=Wiwmj,k (6) Ⅱ)否则,Weibull分布产生区间[-1,1]上随机乘法因子Aj,k有: Ww_owmj,k=Aj,kUiwmj,k (7) Weibull分布生成的随机数实例表现出明显的高突发性,符合天地一体化智能网络流量突发性强的特点,使用该分布产生随机系数因子来构建模型能够更好的描述天地一体化智能网络流量特性. Step 3.2.当Uiwmj,k<0 由式(5)可知,若Aj,k∈[-1,1],那么(1-Aj,k)∈[0,2],则有Uw_owmj+1,2k≤0和Uw_owmj+1,2k+1≤0,通过调整1±Aj,k的取值范围满足需要.因为Uiwmj,k<0,通过控制1±Aj,k为负值来使尺度系数非负.即令(1±Aj,k)∈[-2,0].具体操作如下: Ⅰ)对于Uw_owmj+1,2k=2(-1/2)(1+Aj,k)*Uiwmj,k,要使(1+Aj,k)∈[-2,0],需要将Aj,k的取值范围[-1,1]平移至[-3,1],进而确保尺度系数Uw_owmj+1,2k非负. Ⅱ)对于Uw_owmj+1,2k+1=2(-1/2)(1-Aj,k)*Uiwmj,k,要使(1-Aj,k)∈[-2,0],需要将Aj,k的取值范围[-1,1]平移至[1,3],进而确保尺度系数Uw_owmj+1,2k非负.求尺度小波系数时需要将平移后的随机乘法因子Aj,k带入公式Ww_owmj,k=Aj,kUiwmj,k,将计算的Uiwmj,k和Ww_owmj,k代入迭代公式(4)计算尺度系数Uw_owmj+1,k. Step 4.重复步骤2和步骤3,当计算到最精细尺度j=n下2n个尺度系数结束.每一尺度系数在该模型中确保非负. 为了更好的体现天地一体化智能网络流量的复杂性和真实性,文章利用OPNET和STK设计了一个基于铱星系统的动态网络场景.此场景选用铱星星座和4个地面站模拟了天地一体化智能网络环境,按照铱星的标准对节点和链路进行配置.铱星星座参数如表1所示.通过分析铱星系统的特性来设置星间链路带宽为1Mbps,上行带宽和下行带宽设置为15Mbps.选取其中的3个地面站作为数据发送节点,发送(Voice,Video,Email,Ftp,Http等)数据业务源,数据源每间隔0.003秒的数据速率依次为0.93Mbps,1.22Mbps,1.47Mbps,1.83Mbps,2.05Mbps,3.15Mbps.仿真选用较高流量的目的是模拟智能网络流量的高突发性,第4个地面站作为流量接收节点.并收集该地面站400分钟内的流量时间序列,称该数据集为标签流量.把标签流量信号X(t)输入到W_OWM中. 表1 卫星网络仿真数据Table 1 Satellite network simulation data W_OWM仿真采用matlab分析工具,通过运用matlab进行随机数产生、小波分解、算法流量重构等.该算法中主要包括以下参数:层数,小波函数,乘子范围,乘子分布.W_OWM中的参数设置如表2. 表2 W_OWM中的参数设置Table 2 Parameter setting in W_OWM W_OWM重构标签流量的统计概率密度曲线如图1所示. 验证重构标签流量的概率密度是否符合实际网络流量概率密度分布,分析重构标签流量的统计概率密度分布,由图1可知,W_OWM重构流量中大部分的数据包到达时间分布在0到0.3s之间,累计概率明显超过了90%.重构流量在图中表现为明显的重尾特性.对于到达时间大于0.3s的流量在图中占少数.由此得出,W_OWM重构标签流量概率密度分布体现了天地一体化智能网络流量具有重尾分布特性. 图1 W_OWM重构标签流量统计概率密度曲线Fig.1 W_OWM reconstruction label traffic statistical probability density curve 通常采用Q-Q图来衡量重构流量的分布相似程度.图2对比分析MWM(选取β分布)重构之后的流量与实际流量Q-Q图,对比分析W_OWM(选取Weibull分布)重构之后的流量与实际流量的Q-Q图.选用标签流量作为仿真样本. 图2 重构标签流量与实际流量的Q-Q图Fig.2 Reconstruct the Q-Q diagram of label traffic and actual traffic 对比MWM重构流量和实际流量的分布情况可以得出:只有前期小部分较为接近,大部分偏离45度斜率,由此可以得出,MWM重构的标签流量分布情况偏离实际流量分布.在算法系数构造过程中,MWM采用了没有考虑实际流量特性的β分布,导致重构标签流量的分布特性与实际流量存在差异.W_OWM重构标签流量与实际流量的Q-Q图大部分贴合于45度斜率,在某些地方高度重合.实验仿真表明:W_OWM重构标签流量的分布特性符合实际流量的分布特性,在算法系数构造过程中,W_OWM算法采用了符合重尾分布特性的Weibull分布,通过实验仿真对比发现,W_OWM比MWM更符合天地一体化智能网络流量分布特性. 选用多分形谱对网络流量模型进行尺度分析.选用标签流量数据集作为仿真实验样本,对比分析MWM和W_OWM重构标签流量和标签流量的多分形谱,仿真结果如图3所示. 图3 标签流量建模多分形谱对比Fig.3 Comparison of multi-fractal spectrum of label traffic modeling 仿真结果表明:MWM和W_OWM多分形谱在α<1时贴合于标签流量的多分形谱,结果证明MWM和W_OWM在α<1时能够准确地描述标签流量的多分形性.MWM模型在α>1时的多分形谱与标签流量的多分形谱相离较远.W_OWM模型在α>1时多分形谱曲线在标签流量的多分形谱曲线附近.通过仿真对比发现,在描述多分形谱时,W_OWM的效果优于MWM.W_OWM的多分形谱与标签流量的多分形谱较为接近.在描述流量的多尺度特性时,W_OWM更加准确. 对于随机过程X(t),其自相关系数表示为: ρ=E[X(t+k)X(t)]var[X(t+k)]var[X(t)] (8) 根据式(8)来计算W_OWM和MWM的自相关系数,对比两个模型与标签流量相关系数的结果图如图4所示. 图4 流量模型自相关系数对比Fig.4 Comparison of autocorrelation coefficients of flow models 由自相关对比图可以看出,W_OWM的自相关系数与标签流量的自相关系数较为接近,W_OWM要好于MWM,可以很好拟合标签流量长程相关性,表明在描述长相关特性时,W_OWM更加准确. 文章提出一种基于威布尔分布的混合小波网络流量模型.尺度系数由IWM产生,为了确保流量非负,采用MWM指定随机系数因子.在确定随机系数因子时,文章选取符合天地一体化智能网络流量分布特性的威布尔分布,该模型能够对网络流量行为特性进行准确的描述.仿真结果表明:W_OWM模型在重构精确流量的同时在特性分析上表现较好.W_OWM模型在描述重尾特性、多分形特性和长相关特性得到了较大提升,W_OWM模型重构流量与实际流量的分布相似程度较高.4 基于Weibull分布的混合小波网络流量模型
4.1 模型思想
4.2 W_OWM算法
Uw_owmj+1,2k+1=2(-1/2)*(Uiwmj,k-Ww_owmj,k)
Uw_owmj+1,2k+1=2(-1/2)(1-Aj,k)*Uiwmj,k5 仿真结果和性能分析
5.1 仿真设置


5.2 统计概率密度分析
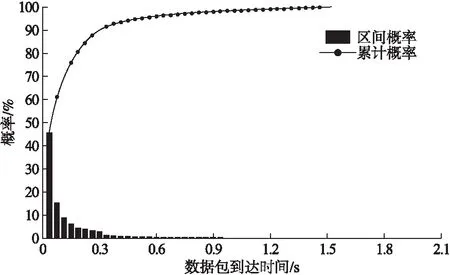
5.3 分布相似程度分析

5.4 多分形谱分析

5.5 相关性分析
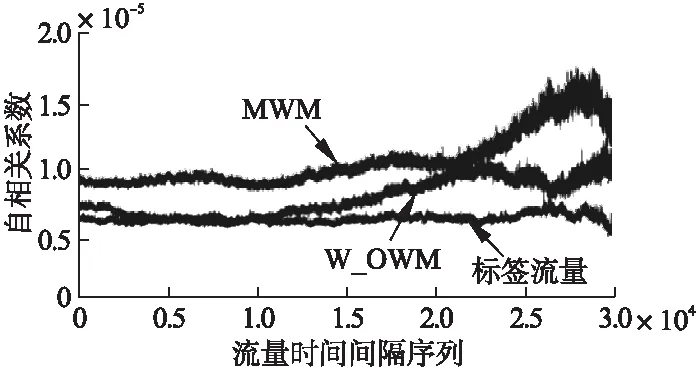
6 结 论

