三级缓冲区结合模糊逻辑的DWA及其应用
郑 维,刘德垚,王洪斌,郝若兰
(燕山大学 电气工程学院,河北 秦皇岛 066000)
E-mail:hb-wang@ysu.edu.cn
1 引 言
随着移动机器人广泛地被用于工业制造,医疗服务,农业生产等领域,如何能在动态复杂环境中为机器人规划路径是现今无人驾驶领域研究的主流问题.轨迹规划可以描述为在信息未知的静态或动态场景中,自主移动机器人利用携带的传感器检测其周围障碍物的实时分布情况从而及时处理环境的变化,从起点安全且无碰撞的行驶到达目标位置[1].机器人行驶时环境信息多变,在有不确定因素出现的环境中为机器人规划出一条安全路径极具实际研究意义和应用价值[2].
Buniyamin提出了用于轨迹规划的简单且有效的PointsBug算法[3].此外,普遍使用的基于模型的轨迹规划的算法包括弹性带结合模型预测轨迹规划器算法[4],多约束模型预测控制[5,6]等等.以上算法[4-6]能预测轨迹,但缺点是需要完善的规划模型以获得良好预测能力.
1996年Simmons首次将轨迹规划问题公式化为速度约束空间的优化问题,提出了曲率速度法[7],在此基础上,2002年Fox等人提出动态窗口法(Dynamic Window Approach,DWA)[8],该方法可以考虑机器人的运动学特性,是一种将轨迹规划问题公式化为速度约束空间的优化问题的模型预测控制算法,能够直接输出速度控制指令,因此,规划的轨迹更平滑且更符合实际对机器人的控制.随后,国内外大批学者加入对DWA算法的研究,2013年Maroti提出了具有目标点距离函数的DWA算法,通过消除多数情况下的局部极小问题提高DWA的评估性能,但由于权重不合理使机器人仍被困住[9].2017年Kintak提出了一种通过计算机器人到障碍物的最小距离和目标角度来计算角速度之差的局部轨迹规划器[10].2018年Abubakr提出利用激光测距仪分析机器人的尺寸与机器人前方自由空间关系的DWA算法,在简单环境中防止了机器人出现狭窄通道打圈震荡问题[11].同年,Vakhshour比较了模糊逻辑和自适应神经模糊推理系统的区别,证明模糊控制器具备自适应神经模糊推理系统随环境的变化联合调整所有权重的功能[12].此外,GIS缓冲区技术是通过描述对象的空间关系和空间行为,为对象的空间查询和空间分析提供参考,近而辅助空间决策的技术[13,14].2020年Jiang等人将缓冲区技术与A*算法结合,算法在静态环境中取得良好的轨迹规划效果[15].上述文献中DWA只应用于静态环境中,当环境是动态时,需要随环境的变化更新DWA评价函数的权重参数.2019年Wang等人提出密集障碍物中的模糊自适应DWA,根据机器人和障碍物间的距离调整速度子函数的权重,但算法中对障碍物的位置分析仍存在不足[16].目前对DWA算法的研究虽取得一定成果,但由于DWA轨迹评价功能的不足,且都未同时考虑根据机器人自身安全性,姿态,预测时间,行驶方向与平均障碍物方向及其与目标位置间的关系等信息调整DWA的轨迹评价值,在未知、动态且复杂的场景中,使用DWA规划出机器人的有效局部行驶轨迹仍具有挑战性.
基于上述研究不足,针对未知、动态且复杂的场景,为规划出机器人的有效行驶轨迹,本文提出基于三级环境缓冲区结合模糊逻辑的DWA算法.首先,改进和增加了DWA的子功能函数.其次,构建三级缓冲区因子并将其纳入DWA算法中,机器人根据自身安全等级调整线速度和角速度;全面考虑时变的环境因素和机器人自身状态,设计模糊控制器,以动态调整机器人的姿态与速度.
2 基本的动态窗口法
2.1 非全向运动模型
建立机器人在时间间隔Δt内运动的非全向运动学模型,t+1时刻移动机器人的位姿如式(1),
x(t+1)=x(t)+vtΔtcos(θt)
y(t+1)=y(t)+vtΔtsin(θt)
θ(t+1)=θt+wtΔt
(1)
式中,x(t)和y(t)为机器人在全局坐标系中t时刻的坐标,θt为机器人在t时刻的航向角,vt和wt分别为移动机器人在t时刻的线速度和角速度.
2.2 速度搜索空间
DWA算法中的3种速度空间约束为:
1)运动学约束:移动机器人的所有可达速度中,最大和最小速度限制为,
Vm=(v,ω)v∈[vmin,vmax]
ω∈[ωmin,ωmax]
(2)
2)电机动力学约束形成的速度约束:电机的有限力矩为机器人在轨迹的预测周期内建立了一个电机的加减约束,从而形成了速度约束如式(3).
Vd=(v,ω)v∈[vc-aΔt,vc+aΔt]
ω∈[ωc-aΔt,ωc+aΔt]
(3)
式中,vc、wc表示当前速度;a、a表示机器人最大加速度.
3)移动机器人安全允许距离的速度约束:为确保机器人与障碍物碰撞前将速度降为0m/s,其制动的速度约束表示如式(4).
Vf=(v,ω)v≤(2d(v,ω)a)12
ω≤(2d(v,ω)a)12
(4)
式中,d(v,w)为(v,w)对应的轨迹与障碍物的最近距离.
速度V的搜索空间应定义如式(5).
V=Vm∩Vd∩Vf
(5)
2.3 评价函数
DWA的最佳速度指令需要满足躲避障碍物、路径长度短并且快速行驶到目标点的要求,因此,基本DWA的轨迹评价函数如式(6).
G(v,w)=σ(α·h(v,w)+β·Od(v,w)+γ·ve(v,w))
(6)
式中,α,β,γ分别表示目标方位角函数、与最近障碍物的距离函数和速度函数的权重系数.σ表示归一化处理.函数h(v,w)用来评估预测轨迹未端机器人的行驶方向与目标位置的角度差.函数Od(v,w)用来评估预测轨迹未端机器人与障碍物的最小距离.函数ve(v,w)是评估移动机器人速度大小的函数,表示如式(7)所示.
ve(v,w)=σ(v)
(7)
最佳的避障速度指令是与最大轨迹评价函数值对应的速度组合,如式(8)所示.
Vcmd=ArgMax{G(v,w)}
(8)
3 评价函数的改进
本文改进了DWA的3种原始子函数的评价功能以提高其轨迹评估能力,同时增加了两种子函数以适应障碍物分布复杂的环境.
3.1 原始子函数的改进
原子函数h(v,w)和Od(v,w)以预测轨迹未端的机器人位置作为参考位置,该位置是机器人在预测时间段T=n·Δt内行驶到的位置,由于速度每隔Δt秒被重新选择,这意味着机器人每Δt秒内只会沿整个预测轨迹的一小部分运动.因此,改进后的子函数h*(v,w)和Od*(v,w)将参考位置设置在接近当前位置的某个位置,与当前位置的距离称为行进距离.首先设置行进距离d,需要根据行进距离d的值和图1中的几何关系确定预测时间段T的数学表达式,如式(9)所示.
T=π/w2r≤d
2arcsind2r/w2r>d
(9)
式中,v和w分别是机器人的线速度和角速度;r=v/w是预测轨迹的半径.

图1 预测时间T的计算方法Fig.1 Calculation method of time period T
改进的函数h*(v,w)和Od*(v,w)机器人的新参考位置都是在预测轨迹中经过行进距离d后的位置.
图2(a)和图2(b)中,最小方形号表示目标位置.在对比轨迹A和轨迹B时,障碍物、目标位置和理想轨迹都相同.以上描述适用于图3-图8.
由图2(a)可知,轨迹A比轨迹B更接近理想轨迹,当参考位置在预测轨迹的末端时,θB,0<θA,0,所以轨迹A 的h(v,w)值较低;若参考位置设置在接近当前位置的某个位置时,θB,n>θA,n,轨迹A的h*(v,w)值更高.

图2 改进的子函数对轨迹的影响Fig.2 Effect of the improved sub-function on the trajectory
在图2(b)中,轨迹A比轨迹B更接近理想轨迹.按照原函数Od(v,w),因为dA,0小于安全距离,所以轨迹A应该被丢弃,且所有和轨迹A相似的轨迹都可能被丢弃,而类似轨迹B的轨迹评价值更高,但类似轨迹A却不会与障碍物碰撞的轨迹不应被丢弃.改进的函数Od*(v,w)在丢弃轨迹时,从轨迹的起点到经过几个时间步长后的位置,计算机器人和障碍物的最近距离,由图2(b)可知,dA,n≈dB,n,且都大于安全距离,因此可以保留这两条轨迹并根据其他子函数进行轨迹评估.
子函数ve(v,w)的功能是评价线速度,改进后的子函数ve*(v,w)由机器人的线速度和角速度共同确定,目的是使机器人尽可能快地行驶并避免不必要的转弯.在相同情况下,线速度越高机器人到达目标位置的速度就越快,因此,无需改变线速度的评价函数,仅在ve(v,w)中增加角速度.在有很多障碍物的环境中,机器人的最佳行为是在没有平移运动的情况下转向目标,因此,以较低的线速度和较高的角速度做转弯运动可以降低与障碍物碰撞的风险.改进后的子函数ve*(v,w)如式(10)所示.
ve*(v,w)=v+(wmax-kvvmaxw)
(10)
式(10)中,角速度中增加vvmax项以测量当前的归一化线速度;k是一个参数;wmax是角速度最大值.
对3项子函数分别进行归一化处理,如式(11)-式(13).
n_h*(v,w)=(h*(v,w)-h*min)/(h*max-h*min)
(11)
n_Od*(v,w)=(Od*(v,w)-Od*min)/(Od*max-Od*min)
(12)
n_ve*(v,w)=(ve*(v,w)-v*emin)/(v*emax-v*emin)
(13)
3.2 增加的子函数
3.2.1 增加的成本函数
基于缓冲区技术建立成本函数osc(v,w),其功能是评价移动机器人的历史轨迹与当前轨迹的接近程度,其目的是增强移动机器人的稳定性,防止机器人返回到已经行驶过的地方或原地绕圈行驶,这在有狭窄通道的环境中避障时十分重要,该函数的权重为μ.成本函数osc(v,w)的评价值越高表示接近程度越低,机器人越不容易在该位置打圈震荡.
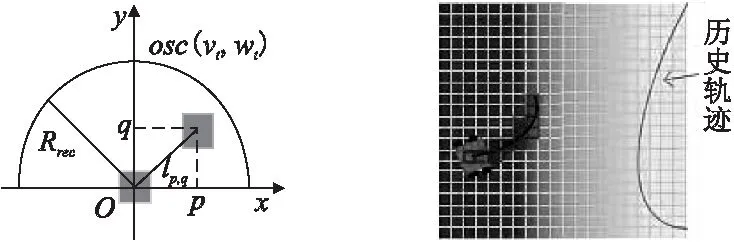
图3 像元成本的更新方法Fig.3 Update method of pixel cost图4 像元计算成本函数值Fig.4 Pixel calculation cost function value
更新机器人位置上或其附近的像元成本的方法如图3所示,图3中的O是t时刻机器人中心位置,以O为原点建立坐标系,Rerc是受机器人影响的半圆形区域的半径,此区域中的像元成本需要被更新;lp,q表示坐标为(p,q)的像元和O点的距离;osc(vt,wt)表示t时刻像元(p,q)应增加的成本,为了防止当机器人的速度变化较大时受机器人影响的周围像元成本迅速增加,在成本的计算中添加速度项,osc(vt,wt)的计算公式如式(14)所示.
osc(vt,wt)=lp,q(1-vt-vt-1vmax)Rrec
(14)
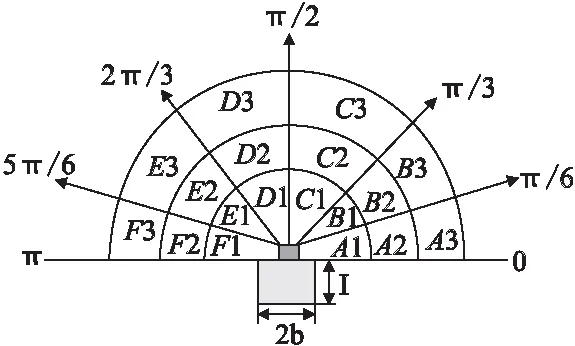
图4示出了历史轨迹和它的像元格组,像元格的颜色越深表示成本越高.函数osc(v,w)的评价值是预测轨迹扫过的像元成本和,对于图4中的预测轨迹,osc(v,w)的评价值是所有被实线圈中的像元格的成本和.图5中对比了轨迹A和轨迹B,图5中的θB>θA且dA,0 图5 增加函数osc(v,w)的轨迹比较Fig.5 Comparison of trajectories of increasing function osc(v,w) 3.2.2 增加的距离函数 子函数Gd(v,w)表示与速度(v,w)对应的预测轨迹末端和目标位置的最小距离,距离越近,Gd(v,w)的评价值越高,该函数的权重为λ.Gd(v,w)的计算如式(15)所示. Gd(v,w)=1-dGdGmax (15) 式中,dG是预测轨迹末端和目标位置的最小距离;dGmax为设定的dG的最大值.如果dG大于dGmax,则Gd(v,w)为负数,此时该项的评价值为零. 改进并增加了子函数后的轨迹评价函数如式(16). G*(v,w)=σα·h*(v,w)+β·Od*(v,w) (16) 利用上文改进的DWA在动态环境中规划轨迹时,对每个子功能的需求都是时变的,需要全面考虑环境因素的变化动态调整各项子函数的权重和预测时间,因此,提出一种三级缓冲区结合模糊逻辑的DWA算法,提供了动态分析预测时间并使用更多场景信息的机会.首先,构建基于三级缓冲区的DWA,使机器人初步根据安全程度调整速度和角速度;然后,分析动态预测时间内的轨迹;最后,全面考虑时变的环境因素和机器人自身状态,设计模糊控制器以动态调整机器人的姿态与速度. 以往研究中认为只要移动机器人不与障碍物相撞,空间就是安全的,但这个想法不够严谨,本文提出了一种更合理的方式是,为机器人构建三级缓冲区,分析不同的安全区域并建立不同的安全系数,机器人距离障碍物较远的区域安全系数更高,而接近障碍物位置的区域安全系数较低. 图6 激光雷达扫描区域划分Fig.6 Lidar scanning area division 面型缓冲区是以面要素的边缘向外扩展所生成的新多边形,三级缓冲区的生成方式是,将机器人用面要素表示,根据激光雷达传感器获取的实际障碍物信息数据设置机器人的缓冲区半径,在DWA轨迹评价函数中构建不同属性的缓冲区因子,从而生成面要素的不同安全程度的缓冲区.具体实现为,机器人通过激光雷达感知障碍物的位置,根据角度的分布情况将激光雷达扫描的前方区域分为6个扇形区域,如图6所示.图6描述了机器人尺寸和车载激光雷达传感器扫描区域.以激光雷达质心为圆心,激光雷达扫描区域横向平均划分成6个角弧度为π/6的扇形区域:A区(A1,A2,A3),B区(B1,B2,B3),C区(C1,C2,C3),D区(D1,D2,D3),E区(E1,E2,E3),F区(F1,F2,F3);纵向划分成三级缓冲区:A1,B1,…,F1表示一级缓冲区,一级缓冲区半径为R1;A2,B2,…,F2表示二级缓冲区,二级缓冲区半径为R2;A3,B3,…,F3表示三级缓冲区,三级缓冲区半径R3. 移动机器人上的激光雷达在执行任务过程中通过判断障碍物到机器人的最近距离ρmin占各级缓冲区的半径的比例,设计缓冲区因子q,如式(17)所示. q=(2e-k1·ρmin-1)/2,R1<ρmin≤R2 (17) 式中,k1,k2,k3∈(0,1)是缓冲区因子的可调参数. 将设计的缓冲区因子q作为参数纳入DWA的速度子函数,使机器人能够初步根据障碍物分布在几级缓冲区,判断自身的安全程度,从而根据当前的安全程度调整速度和角速度.定义三级缓冲区的优势为,避免两个绝对安全的机器人位置由于与障碍物的距离不同而导致二者获取到不同的权值这种情况发生.经过反复试验与调试可知,选择三级缓冲区外部区域的概率更大,这将更有利于产生安全的轨迹. 基于三级缓冲区定义DWA的新轨迹评价函数如式(18)所示. G**(v,w)=σα·h*(v,w)+β·Od*(v,w) +q·γ·ve*(v,w)+μ·osc(v,w) +λ·Gd(v,w) (18) 在DWA执行预测步骤时,计算最佳轨迹是必需的,此轨迹被认为是机器人的新可能位置.需要注意的是,采用较长的固定预测时间,计算成本将大大增加,且环境条件可能会改变.而且,如图7所示,当机器人周围存在许多障碍物时,预测时间段T过长会导致预测轨迹过长,函数Od*(v,w)的误判使得部分可行的速度被丢弃,如轨迹A;某些轨迹朝向目标点但和障碍物距离太近,导致函数Gd(v,w)的误判,如轨迹B.因此,为避免上述问题,需要动态调整d值从而动态调整预测时间T. 图7 时间段T的轨迹分析Fig.7 Trajectory analysis of time period T 综上,在轨迹评价函数中需要动态调整的6个参数分别是:函数的权重组合α、β、γ、λ、μ和行进距离d. 4.3.1 定义模糊控制器的输入函数 本文定义的4个输入函数如下: 1)输入函数Put1: Put1=D (19) 式(19)中,D表示移动机器人中心与目标点的距离. D=ρGdmin+(a(I+2δ))/2 (20) 式中,D∈((-a(I+2δ))/2,R3+(a(I+2δ))/2),参数a表示机器人自身的物理结构参数;I表示机器人的长度;2δ表示在机器人两侧的安全空间余量;ρGdmin表示激光雷达传感器到目标位置的最近距离. 根据目标位置是否在三级缓冲区内,将Put1的模糊集定义为{S,B},即{正小,正大},如式(21), Put1=S,D (21) 式中,R3是机器人三级缓冲区的半径. 2)输入函数Put2: Put2=θr,g (22) 式中,θr,g表示机器人的运动方向与从机器人位置指向目标位置的直线间的夹角. 根据机器人朝目标位置移动的近似偏差将Put2定义为{W,Z,N,O},即{正外,正中,正内,零},如式(23),示意图如图8. Put2=W,θr,g∈[0,π/6)∪[5π/6,π) (23) 图8 Put2的模糊集示意图Fig.8 Schematic diagram of fuzzy set of Put2 3)输入函数Put3: Put3=d (24) 式中,d表示机器人的行进距离,定义d如式(25), d=2vw,w>π (25) 式中,v和w分别是机器人的线速度和角速度. 根据行进距离的长短将Put3的模糊集定义为{S,B},即{正小,正大},见式(26),示意图如图9所示. Put3=S,d>0.5m (26) 图9 Put3的模糊集示意图Fig.9 Schematic diagram of fuzzy set of Put3 4)输入函数Put4: Put4考虑机器人的尺寸,定义障碍物的主方向描述机器人周围障碍物的近似分布. 激光雷达的两个激光束li、lj与障碍物相交的两点间的距离do的计算公式如式(27). do=ρ2j+ρ2i-2cos(θj-θi)ρjρi (27) 式中,ρi和ρj分别是两个激光束li、lj检测到机器人与障碍物的距离,θi和θj分别表示li、lj与水平线形成的角度. 找到近端区A区和F区中的两个最短距离ρAmin,ρFmin和与其对应角度θAmin,θFmin;中端区B区和E区中的两个最短距离ρBmin,ρEmin和与其对应角度θBmin,θEmin;远端区C区和D区中的两个最短距离ρCmin,ρDmin和与其对应角度θCmin,θDmin.根据式(27)计算近端区A和F的dAFo min.同理依次得中端区B和E的dBEo min和远端区C和D的dCDo min,分别计算dAFo min、dBEo min和dCDo min与移动机器人宽度的差,得到DAFmin、DBEmin和DCDmin如式(28)-式(30). DAFmin=dAFo min-a(2b+2δ) (28) DBEmin=dBEo min-a(2b+2δ) (29) DCDmin=dCDo min-a(2b+2δ) (30) 式中,DAFmin,DBEmin,DCDmin∈(-a(2b+2δ),2r-a(2b+2δ));参数a表示机器人自身的物理结构参数;2b和I分别表示机器人宽度和长度; 2δ表示在机器人两侧的安全空间余量. 通常障碍物间的距离越小,机器人靠近障碍物时越危险,所以该距离对应的角度占障碍物平均角度的比例应该越大,因此,用各区的最近障碍物夹角对应的距离倒数作为获得平均角度的权重,障碍物的平均角度θoab是近端区、中端区和远端区角度的加权和,如式(31)所示. θoab=θFmin-θAminDAFmin+θEmin-θBminDBEmin+θDmin-θCminDCDmin1DAFmin+1DBEmin+1DCDmin (31) 图10 障碍物主导方向分析Fig.10 Analysis of the dominant direction of obstacles 图10中θa和θb分别为θoab的两边与水平线的夹角,θmin为最近障碍物方向与水平线的夹角,θn,a和θn,b分别是平均障碍物方向和最近障碍物方向所夹的角度.分析图10中的情况a和b可知,在情况a中,θn,a和θn,b较小,平均障碍物方向可以更准确地反映障碍物的分布;而情况b中在平均方向上没有障碍物,因此平均方向不能反映障碍物的分布,此时,θn,a或θn,b通常较大,用最近障碍物方向θmin反映周围障碍物的分布.障碍物的主方向θo如式(32)所示. θo=θoab,θn,a<π/4 andθn,b<π/4 (32) 将输入函数Put4用公式表示为: Put4=θo (33) 将输入函数Put4的模糊集定义为{O,N,M,F},即{零,正近,正中,正远},如式(34), Put4=N,θo∈[0,π/6)∪[5π/6,π) (34) 式中,ρ表示机器人与障碍物的距离;R3表示三级缓冲区半径. Put1,Put2,Put3和Put4作为4个输入变量,构成C12C14C12C14=64组输入组合,每组输入组合对应一组输出. 4.3.2 定义模糊控制器的输出函数 α、β、γ、λ、μ和行进距离d作为输出函数,它们的模糊集分为五个等级,为{VS,S,M,B,VB},即{正极小,正小,正中,正大,正极大}. 本文提出的三级缓冲区结合模糊逻辑的DWA算法提供了分析预测时间并使用更多场景信息的机会,算法结构如图11所示. 图11 三级缓冲区结合模糊逻辑的DWA算法结构Fig.11 DWA algorithm structure based on three-level buffer and fuzzy logic 操作系统:Windows10,处理器I5,内存8GB及以上,开发环境采用python3.7. 静态环境参数设置:复杂的静态环境参数如表1所示,结合实际,设计地图尺寸为120m×120m的仿真环境空间. 表1 静态环境参数Table 1 Environmental parameter 机器人参数设置(机器人参数设置在全文的仿真中一致):速度分辨率平衡了导航性能与计算成本,机器人的初始速度和姿态角为零,机器人参数设置如表2所示. 表2 机器人参数Table 2 Robot parameter DWA算法初始参数设置(全文统一): α=0.1,β=0.6,γ=0.1,λ=0.1,μ=0.1,d=0.5m,dGmax=50m. 在同一由障碍物离散分布形成的多个狭窄通道的大环境中展示了固定参数下改进评价函数前、后的DWA算法的整体性能,以证明改进评价函数的DWA算法在复杂静态环境的有效性.图12(a)和图12(b)分别示出了基本DWA算法和改进DWA算法对应的移动机器人行驶的轨迹. 图12 复杂的静态环境中移动机器人的行驶轨迹Fig.12 Driving trajectory of the mobile robot 由图12可知,图12(b)中机器人在A处穿过障碍物的狭窄通道,而非绕开A处行驶,机器人在B处穿过障碍物间隙并直接行驶到终点,因此由于子函数Od*(v,w)更改了轨迹的丢弃方式,改进后的轨迹明显更优.图12(a)和图12(b)的C处证明改进后的子函数ve*(v,w)使机器人可以同时考虑线速度和角速度,改进后的DWA算法使机器人在C处以更短的轨迹绕过障碍物.图12(a)和图12(b)的A处轨迹改进前后的对比证明了增加的函数osc(v,w)防止了预测轨迹严重偏向历史轨迹,改进的轨迹在A处并未出现打圈震荡现象,并成功穿过A处;而未增加函数osc(v,w)前,改进前的轨迹落入局部陷阱并保持转弯,并且机器人无法穿过通道A处.对比图12(a)的D处和图12(b)的B处,证明由于增加了子功能Gd(v,w),使机器人的周围有障碍物时向终点运动的趋势增强,改进的轨迹穿过B处后直接向终点行驶,而改进前的轨迹在通道D处的转弯角度明显.改进评价函数的DWA的轨迹长度为198.654m,而基本DWA的轨迹长度为233.758m,改进后的DWA规划轨迹更短. 图12(a)和图12(b)对比证明了固定参数下改进评价函数的DWA的整体性能,改进后的DWA规划轨迹更短且更平滑,提高机器人在复杂环境中到达终点的能力和效率. 针对未知且复杂的动态场景,为验证基于三级缓冲区结合模糊逻辑的DWA算法规划轨迹的有效性,在仿真时使用足够数量且随机分布的动态障碍,动态障碍物空间包括:朝向主机器人行驶的两个圆形移动机器人,速度为1.0m / s;50个位置随机变化的动态障碍物.静态障碍物分布和图12中的相同.复杂的动态环境参数设置如表3所示. 表3 动态环境参数Table 3 Environmental parameter 在图13中,在图12的静态环境基础上,增加了离散分布的动态障碍和两个圆形移动机器人,其中,动态障碍的尺寸和主机器人相同,在图13中可由尺寸的大小明显区分静态障碍和动态障碍;带局部轨迹的方形表示主移动机器人,其周围的圆圈表示一级缓冲区,呈放射型分布的线段表示激光雷达的扫描区域,为更直观地描述障碍物分布位置,激光雷达的显示频率设为每隔2秒显示一次;主机器人的预测轨迹指向反映了其转弯方向.图13(a)-图13(h)分别是提出的三级缓冲区结合模糊逻辑的DWA算法对应不同时刻的主机器人的行驶轨迹,对应的主机器人的速度v和角速度w变化图如图15(a)所示. 如图13(a)和图13(b)所示,在60s和62s时,圆形机器人以1m/s的速度从对面驶来,落入了主机器人的二级缓冲区,同时主机器人周围存在静态障碍和随机出现的动态障碍,主机器人此时的安全度很低,且机器人距离终点较远,动态窗口中的预测轨迹覆盖范围小,在机器人的近端区存在障碍物.这种情况时在缓冲区和模糊控制器的共同作用下,机器人减速行驶,速度由3m/s 降低至1.2m/ s,提高角速度w,不需要考虑因行驶方向偏离终点引起的震荡,因此可以增大预测轨迹与已经行驶过的轨迹的接近程度,减小行进距离d以防止行进距离过长造成障碍物位置误判,保证主机器人有较多的时间尽快转弯,主机器人躲避开第一个圆形移动机器人和其他障碍物,其速度v和角速度w变化图如图15(a)(第8代左右时).同理,如图13(c)所示,在72s时主机器人提前预判第二个圆形移动机器人和随机动态障碍物位置从而调整自身转向,降低速度,提高角速度,顺利躲避了第二个圆形移动机器人和随机动态障碍物,主机器人没有打圈、绕路、碰撞或停车,主机器人的速度v和角速度w变化图如图15(a)(第20左右时).如图13(d)-图13(f)所示,在116-120s时,主机器人需要通过障碍物区B,必须同时躲避周围存在的许多大块障碍物和随机出现的动态障碍物,主机器人调整姿态,降低速度,加强避障作用逃脱了障碍物陷阱区B.如图13(g)所示,在162s时,终点在主机器人三级缓冲区内,且主机器人周围分布许多随机出现的动态障碍,在缓冲区和模糊控制器的共同作用下,主机器人大大降低预测轨迹与已经行驶过轨迹的接近程度以修改主机器人的行驶方向使其指向终点,主机器人顺利躲避了终点附近随机出现的所有动态障碍成功到达终点.主机器人行驶的最终轨迹如图13(h)所示. 图14示出了近些年其他优秀的DWA扩展算法在动态环境中规划的主机器人最终行驶轨迹.图14(a)对应的主机器人的速度v和角速度w变化如图15(b).在图14(a)中,P-DWA ANFIS算法由于的权重系数固定,其对应的主机器人躲避随机出现的圆形移动机器人时需要转弯和减速,主机器人动态避障时绕开障碍物的自由度大,但由于权重固定,虽成功躲避圆形机器人,当主机器人面对密集的障碍物时,从障碍区域的外部绕路到达终点,导致路径长度增加.图14(b)中,A-DWA算法虽采用动态权重,但在这种未知的动态复杂环境下,该算法只考虑障碍物与机器人间的最小距离调整速度子函数的权重,由于机器人对障碍物位置判断不准确,导致该算法对应的主机器人虽然躲避了动态障碍,但无法穿过窄通道A,同时为穿过窄通道B,被强迫选择更能靠近目标点的采样速度,机器人由于朝向和终点方向夹角θr,g>90°而偏离终点,在道口B处出现打圈停滞现象,无法到达终点. 对比图15(a)和图15(b)可知 ,固定参数的P-DWA ANFIS算法对应的主机器人速度和角速度在主机器人行驶过程中出现大幅度波动,且由于权重系数固定,机器人行驶在这种未知动态且复杂的情况下,主机器人动态避障时绕开障碍物的自由度大,h*(v,w)和ve*(v,w)的权重小,导致机器人靠近终点时,主机器人在终点附近仍具有1m/s速度,为避免v较大的轨迹末端超过终点,主机器人不断地调整自身角度导致了w的波动.而提出的三级缓冲区结合模糊逻辑的DWA算法对应的主机器人行驶过程中只有在需要避开两个圆形移动机器人时(第8代和第20代左右)和在通过障碍物B区的时(第37代-77代)减速行驶,在躲避其他动、静态障碍物时保持3m/s的最高速度行驶,在靠近终点时,主机器人的v和w逐渐减至0m/s,且w无上下波动,到达终点后停车,完成了尽快行驶的任务. 图16 从实验视频中截取的真实避障情况Fig.16 Actual obstacle avoidance situation intercepted from the experimental video 综上仿真对比可证,所提出的三级缓冲区结合模糊逻辑的动态预测性DWA算法可以找到未知的动态复杂环境状态下的最佳速度指令,增强了算法的灵活性. 本文实验对象是滑动差分机器人,最大车速为1m/s.车载工控机(迷你小电脑)的CPU类型为英特尔 酷睿i7-5557U,二维激光雷达传感器型号为OBD30M-R2000-B23-V1V17-1L,拥有10m,360°的测量范围,左右两侧各有用于驱动车轮的直流电机. 为验证所提出的基于三级缓冲区结合模糊逻辑的DWA算法在未知的动态复杂环境中轨迹规划中的有效性,在12m×12m的空间中进行了实验,真实实验的视频链接(1)真实实验的视频链接(密码:52119999):https://v.youku.com/v_show/id_XNTAzNTk3NjE1Mg==.html为(密码:52119999):实验环境中放置了多个静态障碍物,两个人依次从车的对面走过模拟仿真环境中出现的两个圆形移动机器人,从实验视频中截取的时刻图如图16(a)-图16(l)所示,移动机器人通过二维激光探测的环境信息,当检测到对面第1个人走来,机器人调整行驶方向,避开第1个人(图16(a)-图16(d));当检测到第2个人从对面走来,此时由于空间狭窄,主机器人周围有铁柱和方桌,同时需要躲避第2个人,因此主机器人减速行驶(图16(e)-图16(h));机器人通过狭窄通道,并躲避开铁柱(图16(i)-图16(k));直至行驶到终点,减速停车(图16(l)).主机器人在整个过程中避开了所有静态障碍物和随机出现的人.与真实实验所对应的主机器人避障轨迹曲线仿真图如图17所示.与真实实验对应的主机器人速度与角速度变化曲线图如图18所示,由图18可知,主机器人在行驶过程中除躲避第2个人时减速(第74代左右),其他时刻均保持以最大速度1m/s行驶. 图17 与实验所对应的主机器人避障轨迹曲线仿真图Fig.17 Simulation diagram of the obstacle avoidance trajectory curve of the robot corresponding to the experiment 图18 与真实实验对应的主机器人速度与角速度变化曲线图Fig.18 Main robot speed and angular velocity change curve corresponding to the real experiment 通过反复实验表明移动机器人可以利用三级缓冲区结合模糊逻辑的DWA算法成功避开动、静态障碍,成功到达终点,整个过程中机器人不会窄通道振荡,打圈和绕路,并与行走的人和静态障碍物保持着安全距离,同时尽快行驶. 本文通过修改和扩展评价函数对基本的DWA进行改进,增强了DWA的规划能力.此外,利用激光雷达技术结合三级缓冲区分析方法创建不同属性的缓冲区因子为机器人设置安全等级;通过设计四输入六输出模糊控制器的方式将目标位置是否在机器人三级缓冲区内、机器人偏向目标位置的程度、行进距离和障碍物的分布情况信息充分地可视化,提出三级缓冲区结合模糊逻辑的DWA算法.使得机器人在实际行驶时进行实时未知的动态复杂避障,同时尽快行驶.最后利用仿真实验对比和实物实验证明三级缓冲区结合模糊逻辑的DWA在未知且复杂的动态环境中规划的有效性.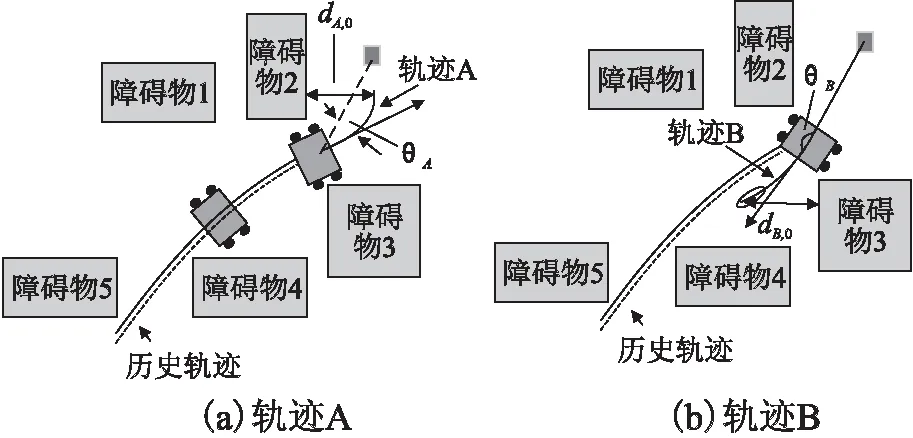
+γ·ve*(v,w)+μ·osc(v,w)
+λ·Gd(v,w)4 三级缓冲区结合模糊逻辑的DWA
4.1 三级缓冲区结合模糊逻辑的DWA
(2e-k2·ρmin-1)/2,R2<ρmin≤R3
k3,ρmin>R34.2 动态预测时间内的轨迹分析

4.3 设计模糊控制器
Z,θr,g∈[π/6,π/3)∪[2π/3,5π/6)
N,θr,g∈[π/3,π/2)∪[π/2,2π/3)
O,θr,g∈else
2vwsinw2,w≤π
B,d≤0.5m

θmin,else
M,θo∈[π/6,π/3)∪[2π/3,5π/6)
F,θo∈[π/3,π/2)∪[π/2,2π/3)
O,ρ>R34.4 三级缓冲区结合模糊逻辑的DWA 算法结构

5 算法的仿真验证
5.1 仿真平台
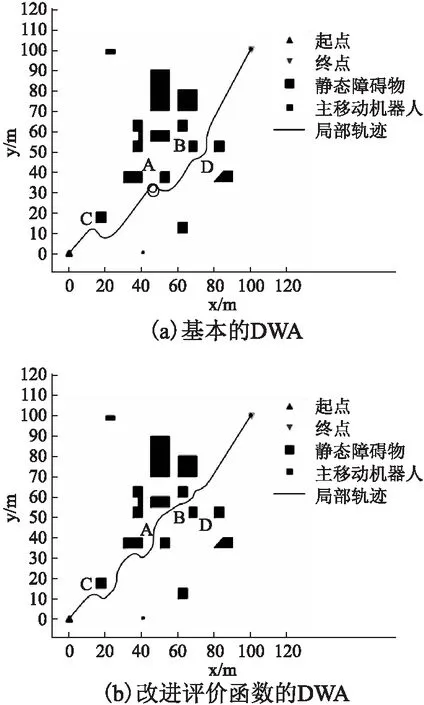
5.2 改进评价函数后算法的仿真验证


5.3 三级缓冲区结合模糊逻辑的DWA算法的仿真验证


6 真实实验验证


7 结 论

