基于模型预测控制与离散线性二次型调节器的智能车横纵解耦跟踪控制*

段敏 孙小松 张博涵

（辽宁工业大学，锦州 121001）

主题词：智能车 离散线性二次型调节器 模型预测控制 跟踪控制 速度规划

1 前言

跟踪控制是无人驾驶汽车领域的研究热点，控制器必须通过同时操纵转向角度、油门和制动来跟踪参考路径和速度。目前，跟踪问题的解决方法有：无模型反馈控制法，这类方法一般不考虑车辆系统的特性，直接根据系统反馈的跟踪误差通过控制律得到前轮转角，例如比例积分微分（PID）控制法，但是该方法因鲁棒性较差需要不断调整参数；纯跟踪（Pure Pursuit）控制法，该控制方法简单易行、实时性好，但需在特定工况下才能有效控制车辆，当面对连续变曲率道路工况时，此方法的跟踪效果较差，难以投入实际工程应用；非线性模型预测控制（Nonlinear Model Predictive Control，NMPC）法，该方法依靠动力学模型设计惩罚函数进行转向与加速，指引车辆实现路径与速度跟踪，此方法虽可在低速工况下保持较高跟踪精度，但由于其在不断循环优化求解的过程中会带来较大计算量，车速较高时存在无法实现对车辆实时控制的风险。Su在轨迹跟踪控制阶段采用了模糊PID 控制，此方式虽然提高了控制的可靠性，但其忽略了对横摆稳定性的控制。Wang等采用自适应模型预测控制提高轨迹的跟踪与稳定性，但其无法适应大曲率工况。Chen等采用一种基于最优前轮侧偏力的智能汽车线性二次型调节器（Linear Quadratic Regulator，LQR）路径跟踪横向控制方法，但其在跟踪小曲率的圆弧路径时仍产生0.2 m 的横向误差，这对实际工程应用来说是难以接受的。

因此，本文在Frenet坐标系下建立二自由度动力学模型设计前馈补偿离散线性二次型调节器（Discrete Linear Quadratic Regulator，DLQR）横向控制器，在一阶惯性系统下设计模型预测控制（Model Predictive Control，MPC）纵向控制器，并通过模糊速度规划使控制系统满足在不同曲率工况下的跟踪精度与横向稳定性，并通过仿真验证其可靠性。

2 自行车模型的建立

2.1 二自由度车辆动力学模型

由于本文对低、高速工况均有涉及，而考虑到轮胎的侧偏特性，高速工况下轮胎会产生较大形变，因此运动学模型不再适用，应以动力学模型作为控制模型，如图1所示（本文坐标系皆采用右手坐标系）。

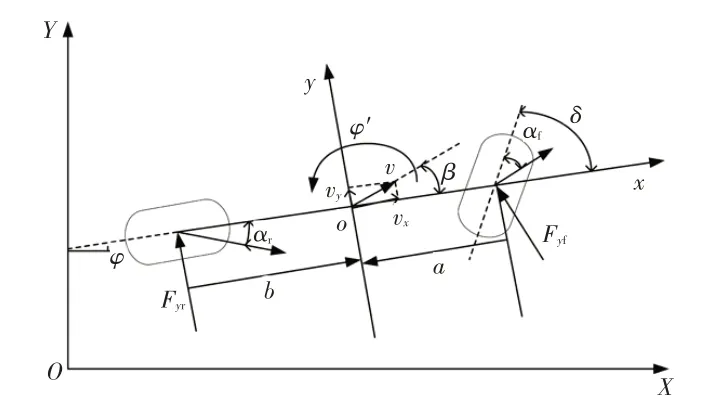
图1 二自由度动力学模型

其中，v、v分别为模型质心处的纵、横向车速，、分别为质心与前、后轴的距离，为质心侧偏角，、分别为横摆角与横摆角速度，为前轮转角，F、F分别为前、后轮所受的侧向力，、分别为前、后轮侧偏角。

假设较小，则cos≈1。对模型进行受力分析：

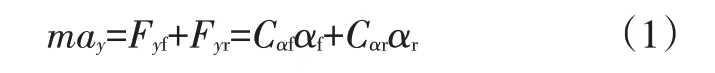
以该模型建立力矩方程为：

式中，为转动惯量；为整车质量；a为侧向加速度；C、C分别为前、后轮侧偏刚度。

根据刚体运动学速度合成与分解可得：

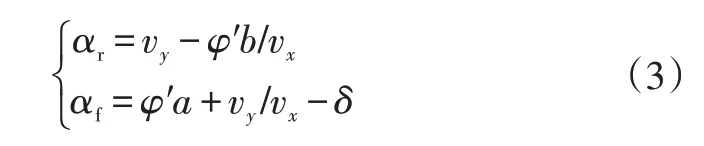
将侧偏角方程代入牛顿第二定律公式可得：

2.2 Frenet坐标系下的横向误差模型

在Frenet 坐标系中，以道路中心线为参考线，以参考线的切向量与法向量建立坐标系，以车辆在参考轨迹的投影点为坐标原点，坐标轴相互垂直，分为方向与方向。相比于笛卡尔坐标系，Frenet坐标系可与轨迹规划的坐标系呼应，大幅简化控制算法，并可起到使纵向控制与横向控制解耦的作用。

图2所示为车辆在Frenet坐标系下的映射，其中、分别为投影点处单位法向量和切向量，、分别为匹配点处单位法向量和切向量，为车辆投影位矢，为车辆真实位矢，为车辆匹配位矢，为横向误差，、分别为车辆在绝对坐标系和Frenet坐标系下的航向角，、′分别为映射前、后的速度。

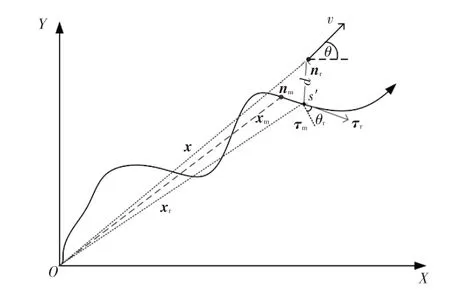
图2 Frenet坐标系

为计算Frenet 坐标系下全局规划路径各离散点的信息，本文寻找与车辆距离最短的目标路径点作为匹配点(,,,)，通过匹配点的信息对车辆在Frenet 坐标系下投影点的信息进行求解。设车辆坐标为(,)，则：

式中，为投影曲率；、为车辆投影位矢的数值坐标；、、、分别为离散轨迹与车距离最近的点在直角坐标系下对应的纵向位置、横向位置、航向角、曲率。

同理，由几何关系可得：

为建立与控制方程间的联系，对求导后由Frenet公式可得：

又因为=+，(-)为小量，化简可得：

将式（9）代入式（7）后，等式两边点乘得：

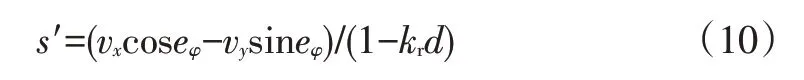
式中，e为航向误差。

e的稳态误差为-，因此，为在控制中使纵向误差收敛于0，且航向误差(-)收敛于0，令纵向误差e=，航向误差e=-以间接达到控制效果。由此，可构成：

代入二自由度动力学方程可得横向误差微分方程：

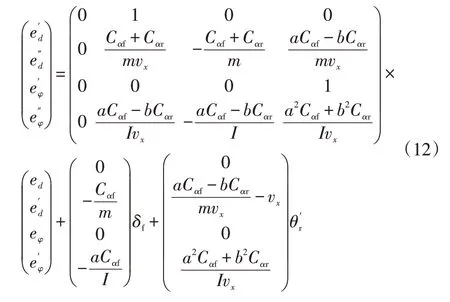
为将控制问题转化为性能函数极小值求解问题，将式（12）按顺序写成：

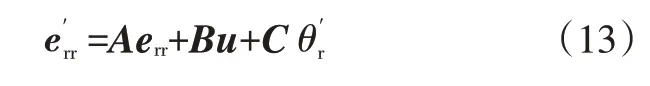
3 跟踪控制器

跟踪控制器整体结构如图3所示。

图3 控制系统结构

3.1 横向跟踪控制器设计

3.1.1 DLQR横向跟踪控制设计

为避免违背连续状态方程式（13）中所满足的牛顿运动定律，实现DLQR 的反馈控制，忽略式（13）中的道路几何信息，对等式两边积分后由中值定理得：

式中，为采样周期；+、分别为积分的上、下限，且在此区间内；()为式（13）两边积分后由牛顿莱布尼兹公式所得移项。

对()采用中点法，对()采用前向欧拉法，可得离散化后的微分方程：

式中，为单位矩阵。

将式（15）按顺序对应简写为离散化状态表达式：

设计性能函数：

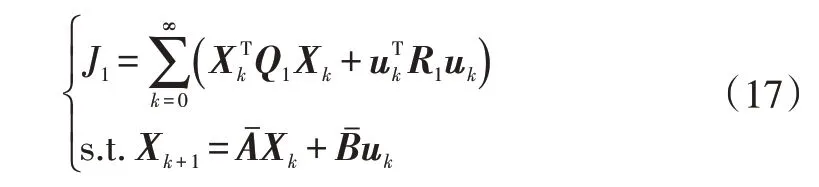
式中，、分别为性能函数对应于状态量与控制量的权重矩阵。

为求二次型的最小值，利用拉格朗日乘子法将其表示为：

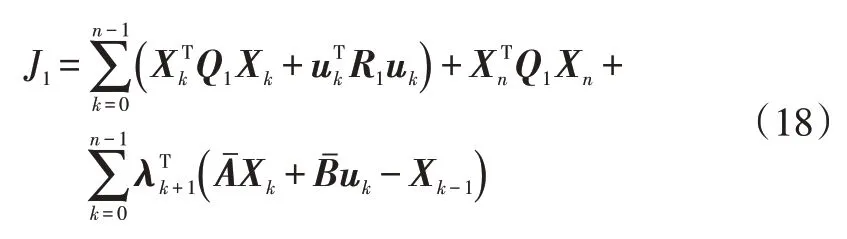
式中，=0,1,2,…,-1；λ为各约束的待定系数；为保证误差的和最小的时段上限，其趋于无穷。

分别对X、u、X、λ求偏导等于0，可得：

设λ=2PX，(=1,2,…,)，且P=，则通过式（19）内等式间的相互代入可得著名的里卡蒂（Riccati）方程的解：

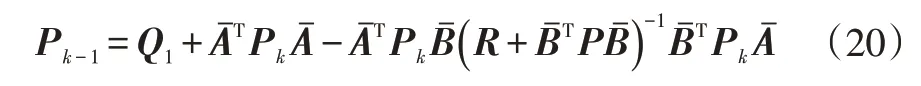
通过迭代求解里卡蒂方程使解收敛后，易得全状态反馈控制：

3.1.2 前馈控制器设计

为消除稳态误差，需要通过额外引入前馈控制，实现存在合适的车轮转角前馈量使尽可能收敛于0的效果，则重新定义全状态反馈控制与误差微分方程：

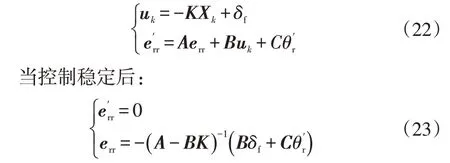
当横向误差e=0时，易解式（23）得车轮转角前馈量：

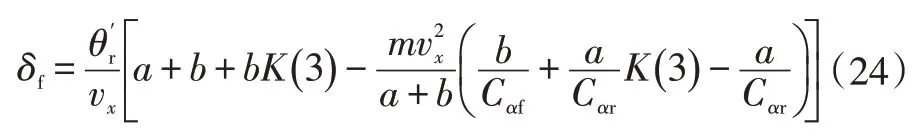
式中，(3)为反馈矩阵的第3列。

3.2 基于MPC的纵向跟踪控制器设计

3.2.1 预测模型的建立

假设车辆横摆运动幅度较小，则有：

以一阶惯性环节来近似表示车辆纵向运动特性：

式中，a为纵向加速度；为a的期望值；为时间常数。

通过前向欧拉法构建离散状态空间，并以速度v作为系统输出，建立输出方程：

式中，()=[v a]；()=；、+1、分别为当前采样时刻、下一周期采样时刻和采样周期。

为了对加速度变化率（Jerk）进行约束，构造状态空间表达式：

由式（28）进行递推迭代可得系统未来时刻的输出：

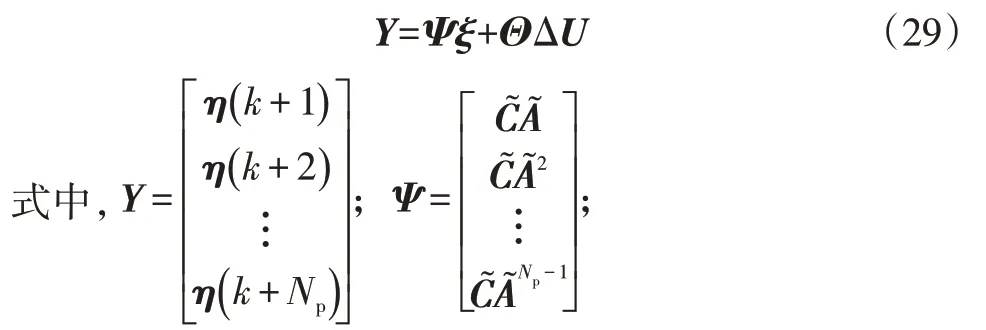
3.2.2 目标函数设计

为在确保速度跟踪精度的同时避免产生大的加速度变化率，定义性能评价函数为：

式中，、为权重矩阵；为系统输出参考量；||·||表示向量的欧几里得范数和矩阵的诱导范数。

通过二次规划的方法解决此优化问题，将式（30）转化为标准二次型：

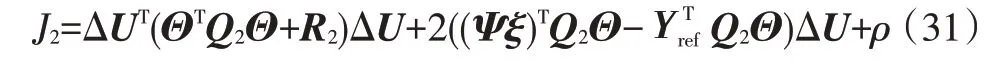
式中，为转化后的常数项，在优化求解中可忽略不计。

该目标函数约束为：

式中，⊗表示克罗内克积；、Δ分别为控制时域内控制量、控制增量的最小值；、Δ分别为控制时域内控制量、控制增量的最大值。

经二次规划（Quadratic Programming，QP）求解器对式（31）、式（32）求解，得到内的控制输入增量：

根据MPC 的基本原理，将控制序列内首元素Δ()作为实际控制输入增量作用于系统：

该控制量被计算至下一时刻，并在新时刻根据状态信息重新预测下一的输出，通过优化过程获得新控制增量序列，如此循环至控制过程结束。

3.2.3 油门制动标定表的制作

基于CarSim-Simulink 联合仿真平台，以油门踏板开度、制动主缸压力为自变量得到(v,a,k)、(v,a,P)的三维数据点，并拟合模型油门踏板开度=(v,a)，制动主缸压力=(v,a)后合并，油门制动标定表如图4所示。

图4 油门制动标定

3.3 基于模糊算法的速度规划

根据驾驶经验，当前方道路曲率较大时，处于高速工况的车辆会产生较大的离心力，且在车辆转向轮的转向角速度约束影响下，被控车辆无法及时转向，易导致车辆操纵稳定性降低与侧向误差增加，甚至造成跟踪失败，严重危及道路安全。因此，车辆在跟踪大曲率目标路径时若出现侧向误差增加的现象，应适当降低车速以提高跟踪效能。反之，可适当提高行车速度。

目前，隶属函数的确定尚未有较为成熟的方法，因此本文通过不断调试确定输入信号采用钟形隶属函数()，输出信号采用三角形隶属函数()时控制效果较为良好：

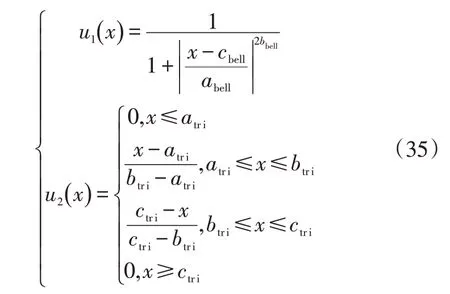
式中，、、为广义钟形隶属函数的参数，其分别决定了隶属度为0.5时的横轴位置、隶属度变化速度和隶属函数中心位置；、、为三角形隶属函数的参数，决定了隶属度曲线3个端点对应的横轴位置。

隶属度函数与模糊规则曲面分别如图5、图6所示，其中横向误差输入的模糊语言为S（小）、M（中）、B（大）、VB（非常大），道路曲率输入的模糊语言为S（小）、M（中）、B（大）、VB（非常大），参考速度输出的模糊语言为VS（非常小）、S（小）、M（中）、B（大）、VB（非常大）、UB（极其大）。

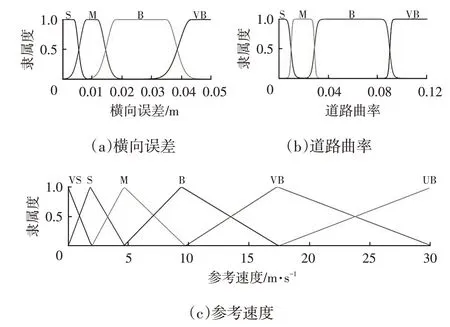
图5 隶属度函数示意

图6 模糊规则曲面

4 仿真验证

4.1 仿真参数

本文控制器使用由Fiala 开发的、由Pacejka 提出的刷式轮胎模型，且忽略在大加速度下轴荷转移引起的前、后轮垂向力分配程度的改变，近似认为轮胎侧偏刚度不发生变化。车辆所跟随的路径信息（道路的横、纵向位置）通过PreScan中的采集车进行采集，仿真路面采用交通量较小的混凝土路面，其路面附着系数为0.75，仿真的主要参数如表1所示，其中依靠以往的经验对泛函、中的权重矩阵选取，权重矩阵的元素取值越大，意味着对应变量的约束要求越高。

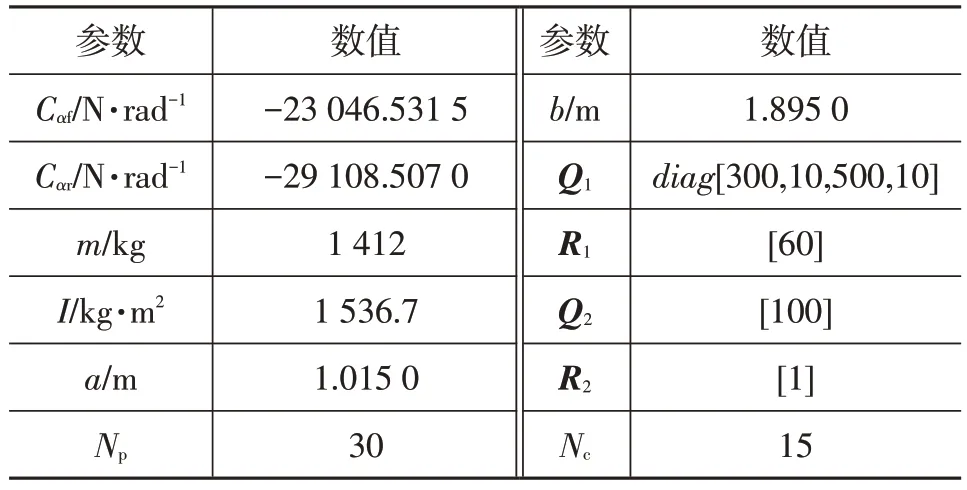
表1 主要参数设置

4.2 横纵联合控制效果验证

在变曲率（仅小曲率突变）路径下对比分析智能车在低速10 m/s、中速16.666 m/s、高速25 m/s 下跟踪精度，结果如图7 所示，在小曲率工况下车辆低速条件下的跟踪误差在8 mm 左右，中速条件下的跟踪误差在10 mm附近，高速条件下跟踪误差在50 mm以内。可以看出，本文控制器的跟踪控制精度非常高。本文仿真时车辆起始位置并不在路径中心线上，Frenet坐标系以车辆在路径上的投影为原点，因此在仿真开始时有固定偏移。

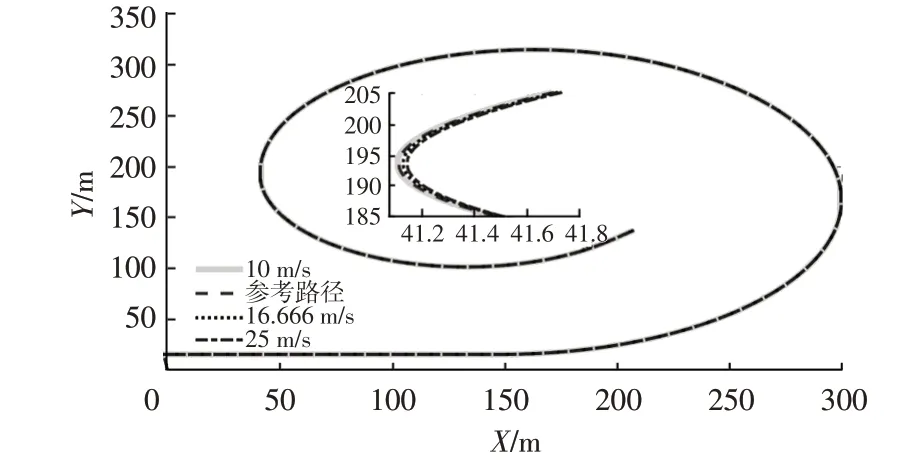
图7 不同车速下的路径跟踪结果

图8～图10所示分别为不同车速下车辆油门踏板开度与横向跟踪误差变化曲线、路径曲率、速度跟踪与纵向加速度变化曲线。可以看出，控制器输出期望加速度后通过油门制动标定表可以精确地实现对速度的跟踪，其中图8中车辆在高速下跟踪路径时横向误差出现的瞬态波动是由于道路曲率突然变大产生的。此外，可以看出该控制器符合速度越快，横向误差越大的客观规律，当车速较小时横向误差可以达到稳态收敛。在10 m/s车速下，横向误差随着路径曲率的逐渐变大，其误差变化范围为0～28 mm，最终趋于稳定。在16.666 m/s 与25 m/s车速下，横向误差也同样遵循此规律，且车速越高，横向偏差波动越大。此外，图9 反映了路径曲率的变化情况，可以看出仿真处于小曲率工况，曲率范围为0～0.011 m。

图8 油门踏板开度与横向误差

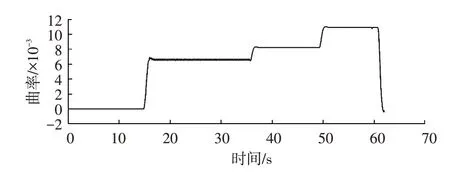
图9 路径曲率

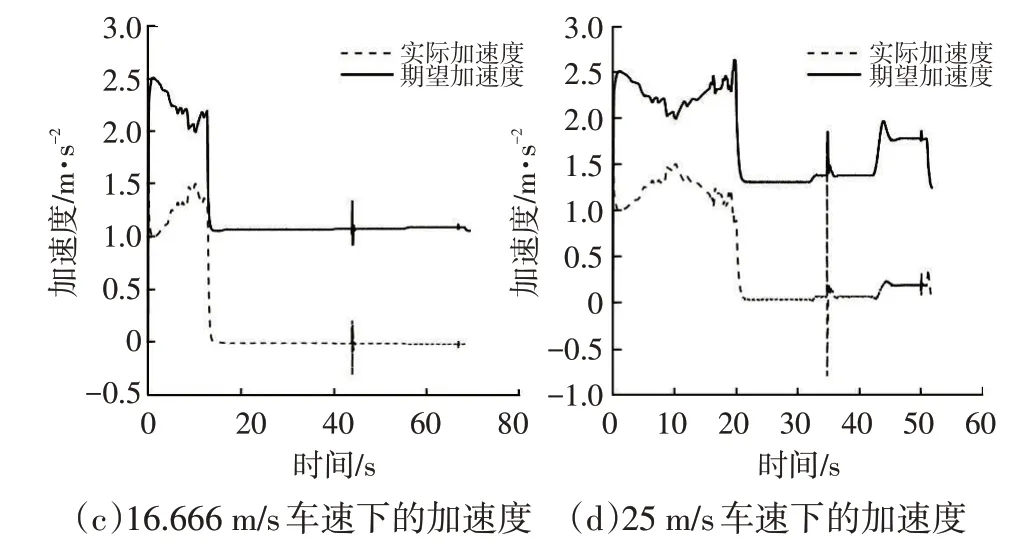
图10 速度跟踪与加速度

图11 为不同车速下转向盘转角的变化曲线，反映了为保证更高的跟踪精度，横向控制器细腻的控制方式使转向盘转角无大幅度、长时间的抖动，也从侧面反映了该控制方式不会对车辆的稳定性造成严重影响。此外，当车速为10 m/s 时转向盘转角在转向时趋于平稳，无明显抖动，随着车速的提高，转向时转向盘的抖动略有增强。

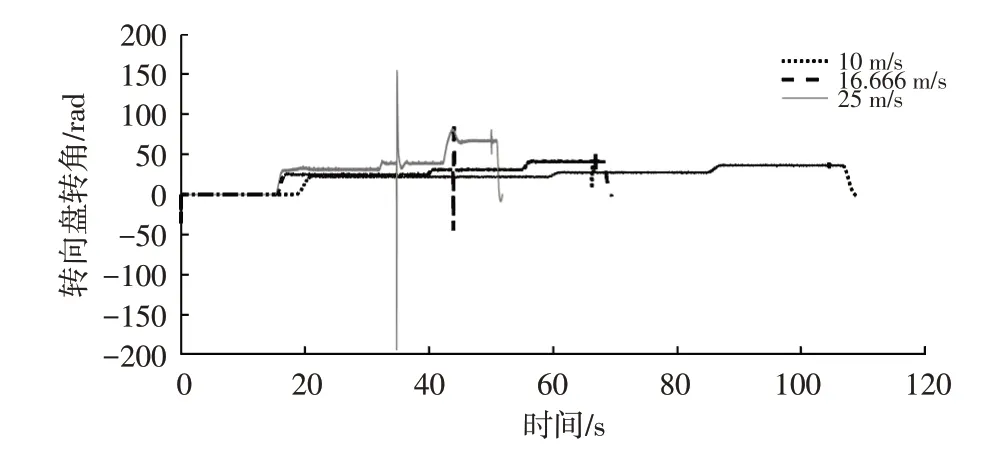
图11 转向盘转角

图12所示为不同车速下的横向稳定性对比，反映了车辆在经过变曲率的路径时质心侧偏角与横摆角速度随车速的提高而增加，但始终在可控范围内，低速时质心侧偏角、横摆角速度在0.01 rad、0.17 rad/s 内循环，高速时质心侧偏角、横摆角速度在0.03 rad、0.32 rad/s 内循环。可以看出本文控制器实现了很好的车辆横向稳定性。

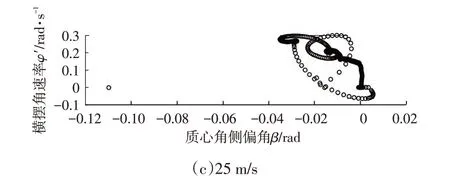
图12 不同车速下的横向稳定性对比

4.3 大曲率工况控制效果验证

在变曲率（大曲率突变）路径下对比分析智能车在10 m/s 与模糊速度规划下的跟踪效果，结果如图13、图14 所示。由图13、图14 可知：在具有模糊速度规划的控制器控制下，车辆跟踪突变大曲率路径时的跟踪误差稳定在100 mm 以内，横、纵向跟踪误差均在50 mm 左右；无模糊速度规划的车辆在道路曲率突变增大时跟踪误差较大，且横向误差在160 mm 左右，纵向误差在300 mm 左右。此外，图13 也反映了在保证跟踪精度的同时，车辆可以更短的时间完成总路径的跟踪。

图13 路径跟踪结果

图14 横纵向跟踪效果

图15所示为有速度规划条件下的速度跟踪与纵向加速度结果，每一时刻对速度的控制皆可达到快速、平稳的效果，速度响应曲线全过程无超调，其中图15a 反映了道路曲率苛刻的变化情况（0～0.08 m）。图15 体现了控制器可对车辆进行精确的纵向控制与其性能的可靠性和优越性。

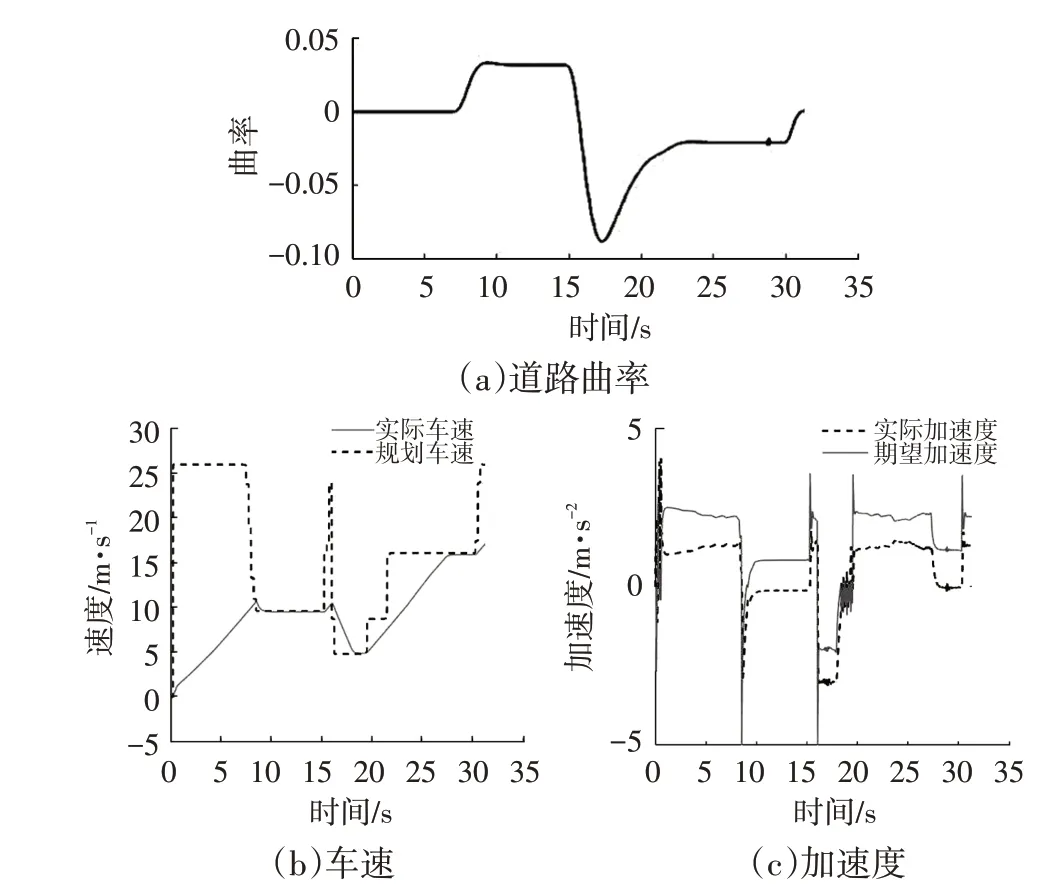
图15 有速度规划下的速度跟踪与加速度

图16 所示为2 种控制方法下横向误差与转向盘转角的变化曲线，在跟踪过程中无模糊速度规划时的路径跟踪在通过变曲率（大曲率突变）路径时横向误差突增至超过1 m，而模糊速度规划下的控制器缓解了这一问题，在转向盘转角方面，其转向弧度更小，约为-4.1 rad，间接反映了具有较好的横向稳定性。

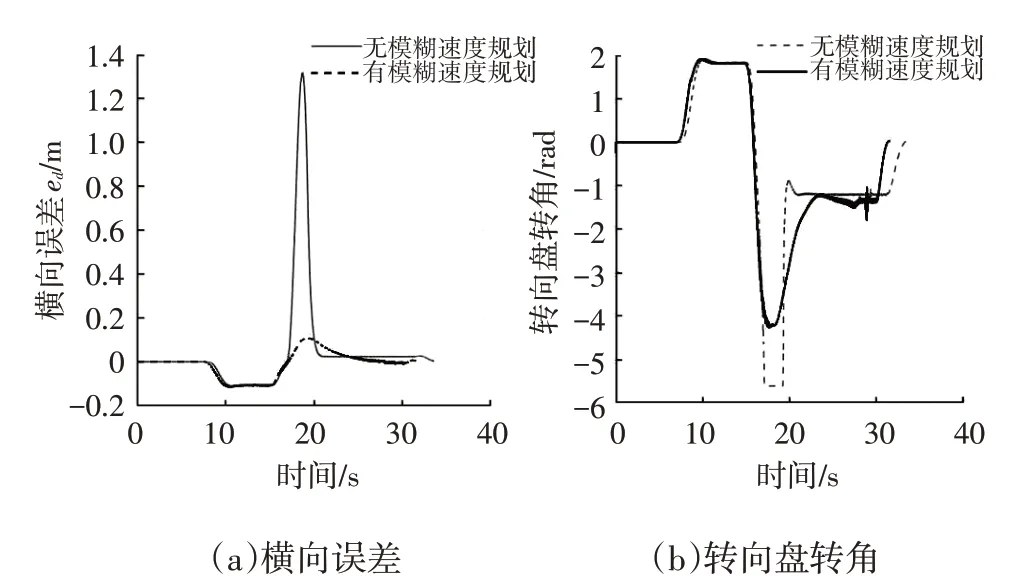
图16 横向误差与转向盘转角

图17 所示为不同控制方式下的横向稳定性对比，其中在速度规划下产生横摆角速度变动区域更小，在-0.55～0.30 rad/s 范围内，其在路径后半段质心侧偏角略有增加，但仍可控，车辆仍具有较高的横向稳定性。

图17 横向稳定性对比

5 结束语

本文为智能车设计了一种路径跟踪控制器，采用DLQR前反馈补偿的方式进行横向控制，同时在模糊速度规划下以MPC 方式进行纵向控制，既保证了小曲率工况下不同车速的跟踪效果，又确保了大曲率工况下仍具有良好的跟踪性能。仿真验证结果表明，横纵跟踪控制器具有较强的鲁棒性，保证了车辆在不同曲率工况下的跟踪精度与横向稳定性，满足实际工程应用要求。