X80 钢级Φ1 016 mm 管道四点弯曲试验数值分析*

0 前 言

随着油气管道建设的快速发展， X80 管线钢管得到了大规模应用， 长输油气管道整体向高钢级、 大直径方向发展

。 目前， 陆上油气管道主要以埋地形式铺设， 其面临的地质灾害是导致破坏失效的主要原因之一

。 地质灾害的发生使油气管道受到内压、 弯曲和拉压等复杂载荷的共同作用， 进而造成油气管道和环焊缝的破坏失效， 严重威胁着管道的安全运行， 目前常采用室内试验的方法研究油气管道在复杂载荷作用下的力学行为和破坏模式。

全尺寸弯曲试验通过对试验钢管施加弯矩引起管道弯曲变形， 从而研究管道的屈曲行为特征， 这是基于应变设计研究中重要的实物试验方法之一

。 通过该方法可以研究完整管道、 环焊缝

、 各种缺陷管道

、 环焊缝缺陷管道

以及修复补强管道

在内压和弯矩组合作用下的力学行为和破坏模式。 全尺寸弯曲试验可以准确模拟管道服役时的工况环境， 试验结果准确可靠。 目前常采用的全尺寸弯曲试验包括两点弯曲试验和四点弯曲试验两种

， 两点弯曲试验标准

规定了试验管道的长度≥6D （D 为管道直径）， 当达到最大载荷时， 试验管道弯曲内弧面上最大应变位置2D 长度范围内的压缩应变平均值即为临界屈曲应变， 该标准规定外载荷的加载间距≥6D。 国内外学者也通过四点弯曲试验方法开展了上述研究

， 基于各自的试验目的和试验设备加载能力， 集中力的作用位置没有明确的规律， 也没有相关规范对其做统一的要求。Guarracino

等在试验过程中发现管道压缩侧的应变与拉伸侧的应变不相等， 深入研究表明， 主要是由于集中力作用处的应变突变改变了受压区的应变分布导致的。 在室内管道全尺寸四点弯曲试验时， 有必要使两个加载压头有足够长的间距来保证研究区域处于单纯的弯曲受力状态以保证试验结果的准确性和唯一性。

本研究通过有限元分析方法， 以X80 钢级Φ1 016 mm 管道为研究对象， 研究了其在全尺寸四点弯曲试验时管道弯矩、 剪力和轴向应变分布规律， 以及管道在加载压头作用处的变形和应变突变范围， 得到了四点弯曲试验加载压头的间距要求。

1 管道全尺寸四点弯曲试验

1.1 四点弯曲试验基本原理

四点弯曲试验是研究构件抗弯性能和弯曲变形力学行为最主要的试验方法， 试验原理如图1所示， 一般常采用3 分点或者4 分点的加载方式。 基于材料力学基本假设， 该试验的计算可简化为一简支梁受两个集中力F 作用， 图1 （a）所示为3 分点加载方式的四点弯曲试验计算简图， 该加载方式下构件的弯矩和剪力分布分别如图1 （b）、 图1 （c） 所示。 由图1 可知， 理想情况下会在两个集中力F 之间的区域产生没有剪力且弯矩为定值的纯弯曲段， 在支座和集中力F之间产生剪力为定值且弯矩线性变化的弯剪段。

古之诗人托物取况，语多精切。如东坡咏海棠云：……山谷咏荼蘼云：“露湿何郎试汤饼，日烘荀令炷炉香。”以丈夫譬花也。崔文靖恒咏黑豆云：“白眼似嫌憎客意，漆身还有报仇心。”以文人烈士譬黑豆，用事奇特，殆不让二老。[10](8册，P244-245)

1.2 管道全尺寸四点弯曲试验

管道主要承受输送油气等介质产生的内压作用， 室内试验时一般在管道两端焊接堵头形成密闭空间， 通过水压加载模拟油气产生的内压P

； 管道在服役过程中会受到环境影响， 从而产生弯曲变形， 室内试验时一般采用双臂弯曲（两点弯曲） 或四点弯曲加载方式模拟服役过程中的弯矩M

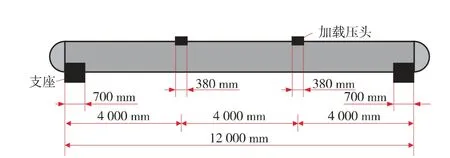
。 管道全尺寸四点弯曲试验装置如图2 所示。 对试验管道施加内压和弯矩， 同时记录试验过程中应变、 位移、 荷载等参数， 最终确定管道的极限荷载、 破坏模式和临界屈曲应变等。

2 管道全尺寸四点弯曲试验数值模拟

随着高钢级、 大直径管道的大量应用以及其在使用过程中出现的各种问题， 有必要研究其在内压和弯矩组合荷载作用下的力学行为和破坏特征。 为全面认识高钢级、 大直径管道在全尺寸四点弯曲试验过程中管道变形、 内力、 应变等随力F（加载压头向下移动产生） 的变化规律， 同时为高钢级、 大直径管道全尺寸四点弯曲试验方法的建立提供理论依据， 本研究开展了高钢级、 大直径管道全尺寸四点弯曲试验数值模拟。 管道采用在实际工程中已大量服役的X80 钢级Φ1 016 mm管道， 根据设计系数计算壁厚分别为12.7 mm、15.3 mm、 18.4 mm 和22mm。

在ABAQUS 有限元软件中建立完整管道全尺寸四点弯曲试验模型， 其中加载压头、 支座和管道的尺寸如图2 所示。 支座内圆弧直径为1 219 mm， 宽度为700 mm， 加载压头内圆弧直径为1 219 mm， 弧长为1/6 周长， 宽度为380 mm。 管道采用多线性随动强化模型， 管道弹性模量为206 GPa， 泊松比为0.3， 屈服强度为638 MPa， 抗拉强度为739 MPa， 密度为7 850 kg/m

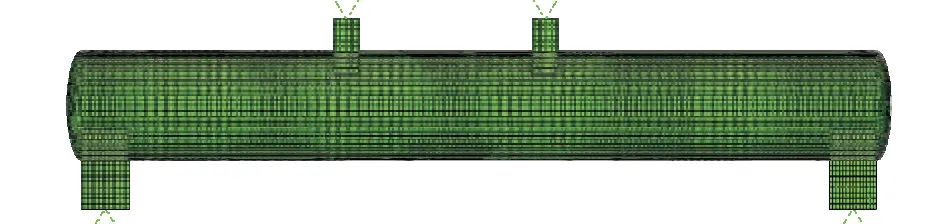
。 管道、 支座和加载压头均选用C3D8R 实体单元， 支座和加载压头设置为刚体， 管体与支座和加载压头之间均采用硬接触。 计算模型如图3 所示。 在计算过程中， 首先施加内压P 达到设计压力10 MPa， 内压采用均布荷载方式施加， 内压作用方向与管道内壁面保持垂直， 通过作动器在加载压头上施加力使管道产生弯曲变形， 直到管道屈服破坏后结束加载。

2.1 数值计算模型

软件基本功能：CPU子系统驱动包括按键驱动、LCD显示驱动、看门狗驱动、与FPGA通信驱动；以驱动为基础，完成计数并显示、实时人机交互、发送数据给FPGA、中断接收FPGA命令进行操作。FPGA仲裁子系统驱动包括按键驱动、LCD显示驱动、蜂鸣器驱动、与CPU通信驱动、切换驱动；以驱动为基础，完成实时人机交互，与CPU数据交互，自动或手动切换、报警提示、仲裁控制输出。

2.2 管道弯矩和剪力分布

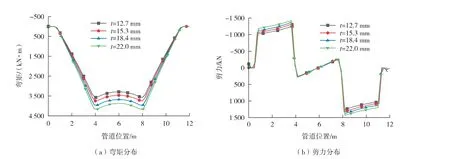
内压P=10 MPa、 F=2 000 kN 作用下， 管道弯矩和剪力分布如图4 所示。 通过对比图4和图1 可知， 管道在四点弯曲试验过程中， 弯矩和剪力的分布基本和理论计算结果一致。 在支座和加载压头之间， 弯矩分布近似为直线，剪力分布近似为水平直线； 在两个加载压头之间， 弯矩分布近似为水平直线， 剪力分布为直线且数值较小。 弯矩和剪力都是从支座内侧开始出现， 弯矩的极值出现在加载压头内侧， 剪力极值出现在加载压头外侧。 在相同大小力作用下， 弯矩和剪力的最大值随着壁厚的增加而增加； 随着壁厚的增加， 在加载压头内侧易出现弯矩的最大值， 在加载压头外侧易出现剪力的最大值。 因此， 从内力角度来说， 在进行四点弯曲试验过程中， 两个加载压头之间的管道满足纯弯曲条件。

2.3 管道轴向应变分布

在内压P=10 MPa、 力F=2 000 kN 的作用下，管道轴向应变分布如图5 所示， 由于管道在弯矩和内压力的共同作用下产生应变， 因此， 图5 中的轴向应变为不同管道位置总应变减去内压产生的应变。

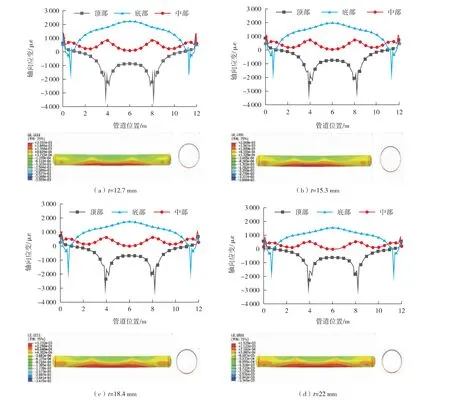
由图5 可知， 不同壁厚的管道具有类似的应变分布规律， 即在两个加载压头之间的管道下侧受到拉应力， 管道上侧受到压应力。 加载压头和支座处的管道产生压应变， 该压应变区域的范围大于加载压头和支座的宽度。 同时管道为空心截面， 加载压头作用处的管道截面几何形状会发生改变， 引起一定范围内其他截面几何形状发生改变， 故该压应变区域的范围大于加载压头和支座的宽度。

其他模相合系数为0, 像s1,1,0, s2,2,1等. 我们发现该线性增长率与重力加速度g和球界面初始半径r0有关: 随着重力加速度的增大而增大, 随着初始半径的增大而减小. 而这些非零模耦合系数与g无关, 只与初始半径有关: 随着初始半径的增大而减小.

适性课堂“一二·三六”教学模式以“适性教育”为理念，以适合学生的“学”为中心，通过“一个目的、两种方式、三个阶段、六个环节”开展，能够真正将学生作为课堂教学的主体，促进学生综合能力的全面提升。

产生上述应变分布的主要原因如下： ①管道为空心截面， 在弯矩作用下， 截面几何形状变成椭圆， 导致截面抗弯刚度发生变化

， 未加载时， 管道的每个截面几何形状相同， 即每个截面的抗弯刚度相同； 随着加载的进行， 由于截面成椭圆状， 每个截面几何形状各不相同， 导致每个截面的抗弯刚度不同， 进而导致纯弯曲段的应变分布为一条曲线。 ②相同外径不同壁厚的管道， 抗弯刚度随着壁厚的增加而增大， 在相同力的作用下， 壁厚大的管道轴向应变小。 ③管道为空心截面， 在一定宽度的加载压头作用下， 在加载压头作用处轴向一定范围内， 管道的截面几何形状会发生改变， 同时发生应变突变， 且该范围随着壁厚的增加逐渐减小。

3 加载压头对管道轴向应变分布的影响范围

管道全尺寸四点弯曲试验除了研究完整管道在内压和弯矩共同作用下的力学行为， 还被常用于研究环焊缝、 环焊缝缺陷管道和修复管道在内压和弯矩共同作用下的力学行为

。 为保证研究区域处于单纯的弯曲状态， 从而分析弯曲对其的影响， 须保证两个加载压头间距足够大， 进而研究加载压头作用下管道轴向应变分布的影响范围。

3.1.1 数值计算模型

3.1 壁厚对管道轴向应变分布的影响

管道全尺寸四点弯曲试验中， 加载压头附近管道的轴向应变突变是由弯矩M 和加载压头作用力F 共同作用引起的， 在实际分析、 试验和计算时， 很难将两者产生的效应剥离开。 因此， 采用如图6 所示的加载方式和约束方式计算在加载压头作用力下， 管道轴向的应变突变范围。 虽然该加载条件下管道的力学行为与四点弯曲试验中力单独引起的管道的力学行为不完全一致， 但其可以表征管道在加载压头单独作用时的影响范围和变化规律， 或者可以认为该影响范围为四点弯曲试验中加载压头影响范围的上界。

在ABAQUS 有限元软件中建立加载压头作用下管道的分析模型， 如图6 所示。 加载压头、 支座和管道等的尺寸如图7 所示。 加载压头和支座内圆弧直径为1 219 mm， 弧长为1/6 周长， 宽度为380 mm， 建立4 组模型， 管体壁厚分别为12.7 mm、 15.3 mm、 18.4 mm 和22 mm， 其他参数设置与2.1 节一致。 在计算过程中， 首先使内压P 达到设计压力10 MPa， 然后逐渐增大加载压头的作用力， 直至达到设定值2 000 kN 后结束加载。

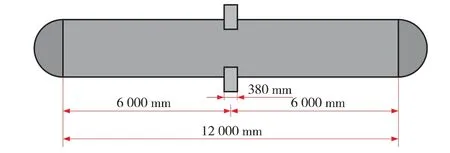
3.2.2 应变分布

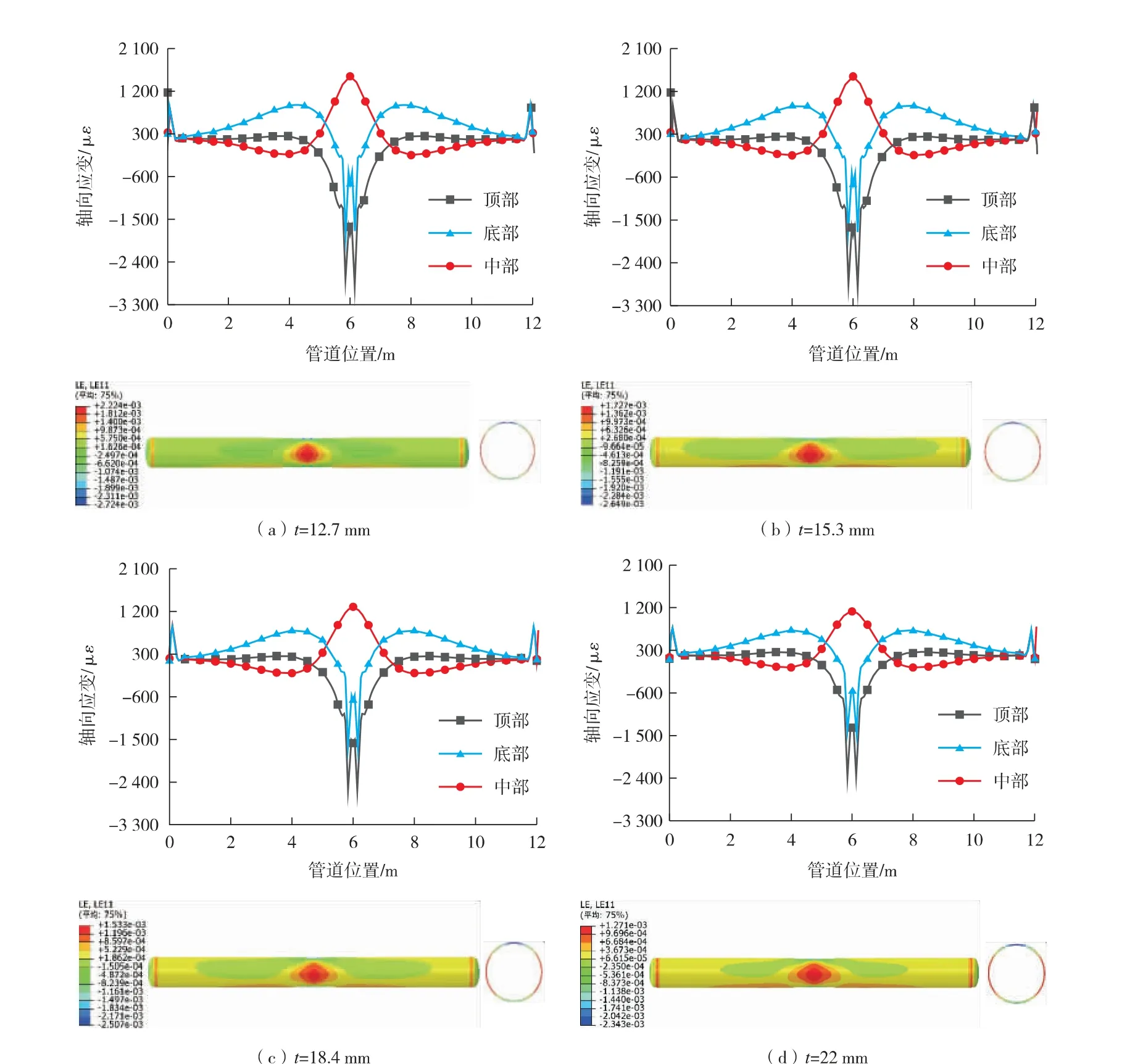
在设计内压10 MPa 和2 000 kN 力作用下，管道轴向应变分布如图8 所示。 从整体应变分布来说， 4 组管道的应变分布规律较为接近， 即在加载压头处会产生应变突变并产生一定范围的影响， 同时， 管道不同部位的轴向应变随着壁厚的增加而减小。 从顶部、 中部和底部3 个典型区域的轴向应变沿长度方向的分布看， 加载压头的作用会使管道在顶部和底部产生受压区域， 中部产生受拉区域， 并影响一定的范围； 由于变形协调， 加载压头处顶部和底部应变为压应变， 其沿轴向先变为拉应变后最终趋于0； 加载压头处中部应变为拉应变， 其沿轴向方向先变为压应变后最终趋于0， 可见在加载压头作用处管道的轴向应变变化非常复杂。 离加载压头中点超过2 m以后， 所有应变都随着距离的增加而逐渐减小， 加载压头产生的强影响范围在2 m 以内。

加载压头处管道的顶部和中部轴向应变有明显突变， 支座处管道的底部轴向应变有明显突变； 加载压头处管道的顶部和中部轴向应变极值及其应变突变范围随壁厚t 的增加逐渐减小， 支座处管道的底部轴向应变极值随壁厚t 的增加逐渐增加。 管道中部区域， 顶部应变分布基本为一条水平直线， 底部应变分布为一条曲线， 中部应变分布为一条接近于0 的曲线； 管道中部区域的顶部和底部应变极值随壁厚的增加逐渐减小。 由于管道底部远离加载压头的影响， 两个加载压头之间的底部应变分布没有突变； 加载压头中点左右各1 m 范围内的顶部和中部应变有较大的突变， 管道中部2 m 范围内区域的应变分布没有突变。 由此可知， 从轴向应变角度来说， 四点弯曲试验时管道中部2 m 范围的区域满足纯弯曲条件。

3.2 F 大小对管道轴向应变分布的影响

3.2.1 数值计算模型

“周末，我们经常随援疆工作组下团场，和团场的教师进行交流和探讨。”盛庆余说，“我们会有针对性地安排相关学科教师到团场中学开办学科讲座，与基层教师集体交流、志愿结对，将内地的教育教学理念和方式方法分享给他们。”一年多来，他们几乎走遍所有团场，“高效6+1”课堂模式也渐渐被七师教师接受认可。

选取壁厚为15.3 mm 的管道建立管道在加载压头作用下的计算模型。 其他参数与3.1 节一致。 在计算过程中， 首先使内压P 达到设计压力10 MPa， 然后逐渐增大加载压头上的作用力，直至达到设定值3 000 kN 后结束加载。

3.1.2 轴向应变分布

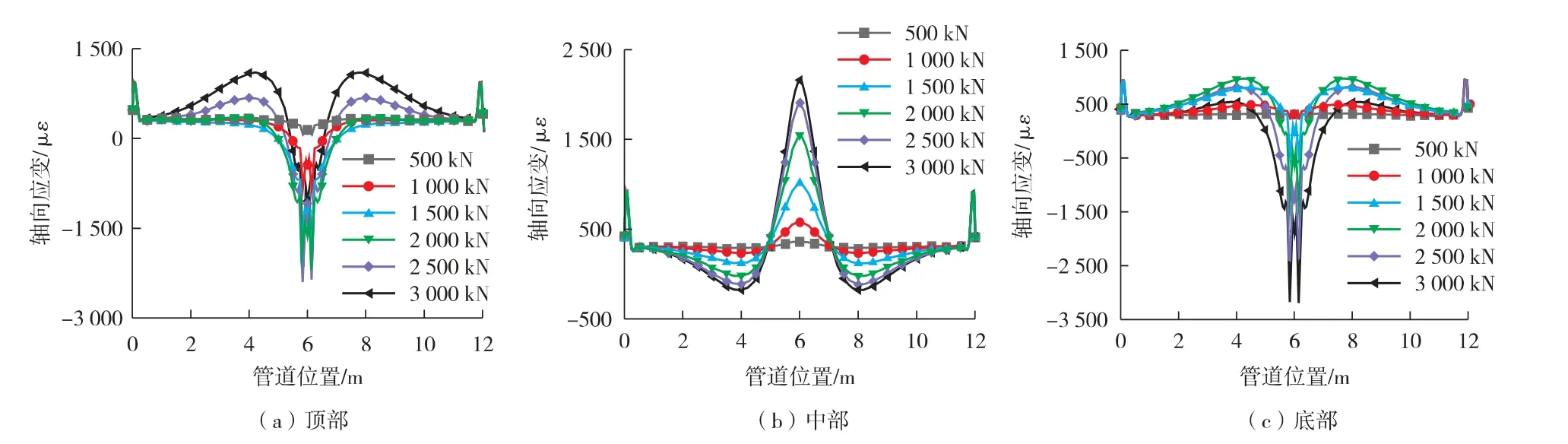
在10 MPa 的内压和3 000 kN 力的共同作用下， 管道轴向应变分布如图9 所示。 由图9 可知， 不同大小的力的作用下各个典型区域的轴向应变分布形状基本一致， 轴向应变最大值均出现在加载压头中点处。 加载压头影响区域的应变极值基本都出现在距加载压头中点2 m 位置处； 在加载压头尺寸一定的情况下， 加载压头的影响区域及其应变极值位置不随力的增加而改变。

4 结 论

（1） 从内力角度， 四点弯曲试验时， 两个加载压头之间的管道满足纯弯曲条件。 支座和加载压头之间的弯矩分布近似为直线， 剪力分布近似为水平直线； 两个加载压头之间， 弯矩分布近似为水平直线， 剪力分布为直线且数值较小。

水平集法最早是由Osher和Sethian[20]在描述曲线或者曲面的演化过程中提出的.其基本思想是将结构边界隐式地表达成高维尺度函数中的零水平集，本质上可以看作是一种形状优化的方法.通常用在边界变化复杂或者灵活的结构中.水平集优化方法通常转化成三维问题的优化设计，表示二维曲线嵌入到三维空间的水平集函数中[21].

（2） 从轴向应变角度， 四点弯曲试验时管道中部2 m 范围的区域满足纯弯曲条件。 两个加载压头之间的管道下侧受拉应力作用， 管道上侧受压应力作用。 加载压头处的顶部和中部轴向应变有明显突变， 支座处的底部轴向应变有明显突变。

本研究病例为2012年1月—2018年4月在我院门诊就诊或住院患者57例，其中男性40例，女性17例，年龄51～91岁，平均年龄（69.9±8.9）岁。主要临床表现为不同程度的头晕、上肢麻木、无脉、患侧上肢乏力，双上肢血压压差＞20mmHg。

（3） 加载压头处管道会产生应变突变并产生一定范围的影响。 在相同力的作用下， 不同壁厚的管道具有类似应变分布规律， 轴向应变随着壁厚的增加而减小； 在不同力的作用下， 轴向应变分布基本一致， 加载压头影响区域及其应变极值位置不随力的增加而改变。

（4） 管道四点弯曲试验时应保证加载压头有足够的间距才能保证试验管道中部有足够长的区域处于纯弯曲受力状态。 长度为12 m、 X80 钢级、 Φ1 016 mm 管道在四点弯曲试验时， 应保证加载压头间距≥4 m， 从而保证管道中部至少有2 m 长的区域满足纯弯曲条件。

[1] 冯耀荣，吉玲康，李为卫，等. 中国X80 管线钢和钢管研发应用进展及展望[J]. 油气储运，2020，39（6）：612-622.

[2] 张杰. 典型地质灾害下油气管道力学行为研究[D]. 成都：西南石油大学，2016.

[3] 刘鹏，李玉星，张宇，等. 典型地质灾害下埋地管道的应力计算[J]. 油气储运，2021，40（2）：157-165.

[4] GUARRACINO F，FRALDI M，GIORDANO A. Analysis of testing methods of pipelines for limit state design[J].Applied Ocean Research，2008，30（4）：297-304.

[5] 孙彦彦，李昕. 在内压和弯曲载荷下钢管临界屈曲应变的确定[J]. 油气储运，2013，32（9）：1022-1026.

[6] 陈小伟，张对红，王旭. 油气管道环焊缝面临的主要问题及应对措施[J]. 油气储运，2021，40（9）：1072-1080.

[7] 王涛. 全尺寸大变形海底管线环焊缝弯曲性能研究[D].天津：天津大学，2014.

[8] 冯欣润. 复合载荷下缺陷海管剩余极限强度研究[D].武汉：武汉理工大学，2019.

[9] SHUAI Y，WANG X H，CHENG Y F. Buckling resistance of an X80 steel pipeline at corrosion defect under bending moment[J]. Journal of Natural Gas Science and Engineering，2021（93）:104016.

[10] BASTOLA A，WANG J，SHITAMOTO H，et al. Investigation on the strain capacity of girth welds of X80 seamless pipes with defects[J]. Engineering Fracture Mechanics，2017（180）：348-365.

[11] SORET C，MADI Y，GAFFAR D V，et al. Local approach to fracture applied to the analysis of a full size test on a pipe containing a girth weld defect[J]. Engineering Failure Analysis，2017（82）：404-419.

[12] 余东亮，杨川，吴东容，等.X80 管道环焊缝缺陷钢质环氧套筒补强试验[J]. 油气储运，2021，40（9）：997-1007.

[13] 李鑫，谢萍，王琴，等. 两种全尺寸弯曲试验设备的对比分析[J]. 石油管材与仪器，2021，7（2）：86-90.

[14] 石油管材专业化技术委员会. 油气输送管特殊性能试验方法：第3 部分 全尺寸弯曲试验：SY/T 7318.3—2017[S]. 北京：中国标准出版社，2017.

[15] 王慧平. 联合荷载作用下海底管道的弯曲破坏特性研究[D]. 大连：大连理工大学，2016.