Copula 函数模型的汽车偏置碰前纵梁结构可靠性分析①

俞陆新， 崔 强， 柳 砚， 唱志强

(1.安徽机电职业技术学院机械工程学院，安徽 芜湖 241000；2.奇瑞商用车汽车有限公司，安徽 芜湖 241000)

0 引 言

汽车碰撞事故中，偏置碰撞相对高发且很容易造成乘员舱变形，对驾驶员和副驾驶乘员的腿脚部造成严重伤害。车身结构中的前纵梁在碰撞过程中，承载吸收了大部分能量。因此，就汽车碰撞安全性能而言，对前纵梁进行可靠性分析具有重要的意义。近年来，基于可靠性分析的汽车结构耐撞性优化设计已得到较多关注，吕晓江等研究了多目标可靠性的车身耐撞性，姜平等将近似模型应用到汽车耐撞性的研究中，还有一些学者基于鲁棒性和近似模型稳健设计方面做了一定的研究[1-4]。上述研究，未充分考虑设计部件之间的相关性。以某轿车前端结构为例，充分考虑分析设计变量间的相关性，优化搭建基于Copula函数的有限元模型，同时引入证据理论BPA分析[5]。通过对CNCAP汽车偏置碰仿真过程，分析获得前纵梁和前吸能盒在此工况下的结构可靠性。

1 Copula函数可靠性分析的理论基础

1.1 Copula函数

Copula函数能很好的描述随机变量间的耦合特性，其本质上可理解为一种连接函数[6]。即：

C(μ1,…,μn)=Pr{U1≤μ1,…,Un≤μ}

(1)

式中，Ui～U(0,1),i=1,2,…,n,

为标准均匀分布。

Copula函数的种类较多，车身前纵梁结构中涉及到多个变量相关，变形失效过程也较为复杂。故选用目前应用较为广泛的Archimedean Copula函数模型 ,因其表述简洁，且能够反馈的相关性范围广[7]-[9]。

定义：设φ是[0,1]→[0，∞]上的连续、严格单调减少、下凹函数，且φ(1)=0，则称：

C(μ1,μ2,…,μn)=

φ[-1](φ(μ1)+φ(μ2)+…+φ(μn))

(2)

且由生成元φ生成的Archimedean Copula 函数，

其中φ[1]为φ的伪逆，定义为：

(3)

若φ(0)=∞，则φ[-1]=φ-1。

1.2 证据理论原理

证据理论(evidence theory)即利用上、下限概率解决多值映射问题，引入信任函数概念，形成了基于“证据”和“组合”来处理不确定性推理的数学方法。可用信度函数(belief function，Bel)和似真函数(Plausibility function，PI)来反描述此不确定性，其对应函数表达式如下：

(4)

信度函数和似真函数构成的区间[(Bel),(PI)]就表示对命题的不确定度信任区间，代表证据的不确定程度，如图1所示。在证据理论框架下，两组独立mass函数可以通过Dempster组合规则进行数据融合。

图1 证据可信度区间

2 可靠性分析流程与模型建立

2.1 偏置碰撞的可靠度分析流程

在偏置碰撞的优化设计流程中，将Copula函数应用于近似模型的搭建。在设计变量的波动范围内，偏置碰撞的Copula函数优化设计流程图如图2所示，具体的流程如下：

图2 偏置碰撞的稳健性优化设计流程图

(1)首先，搭建满足精度要求的汽车偏置碰碰撞仿真模型；

(2)确定设计变量的样本值和基本信度分配BBA；

(3)运用Copula函数分析，考虑设计变量的变化和彼此间的联系；

(4)利用贝叶斯方法对Copula进行分析优化；

(5)上述迭代分析获得结构可靠性区间[Bel(A)，PI(A)]。

2.2 仿真模型的搭建与验证

以某轿车为例，参照C-NCAP(2018年版)试验标准，设置工况为40%刚性墙壁碰撞，模拟碰撞速度为64km/h。整车整备质量为1170kg,质心为(1095.7，-12.0，249.9),整备质量下质心距前后轴距离比为2:2.46。在LS-DYNA软件中建立了该车ODB碰撞有限元模型，如图3所示；碰撞后试验与仿真整车加速度对比见图4。由图4可知，碰撞后仿真与试验变形模式基本一致，整车加速度变化趋势基本相同，搭建的仿真模型可用于后续优化设计。

图3 偏置碰撞有限元模型

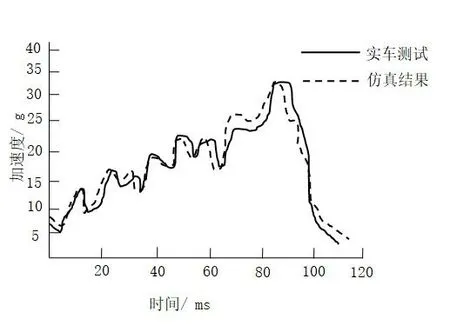
图4 实车与模拟左B柱加速度变化趋势图

3 优化过程及结果

3.1 设计变量

碰撞事故中，偏置碰撞占比较高，且容易导致乘员伤亡。偏置碰撞时，前舱压溃变形，向后挤压对防火墙后端的乘员空间侵入量过大。此过程中，主要的受力吸能部件是前吸能盒和前纵梁。材料定义为冷轧高强度钢B340LA，如图5所示以其厚度设计尺寸为设计变量：前纵梁内板料厚、前纵梁外板料厚χ2、前吸能盒内板料厚χ3、前吸能盒外板料厚χ4为设计变量,其基本信度分配BBA如表1所示。

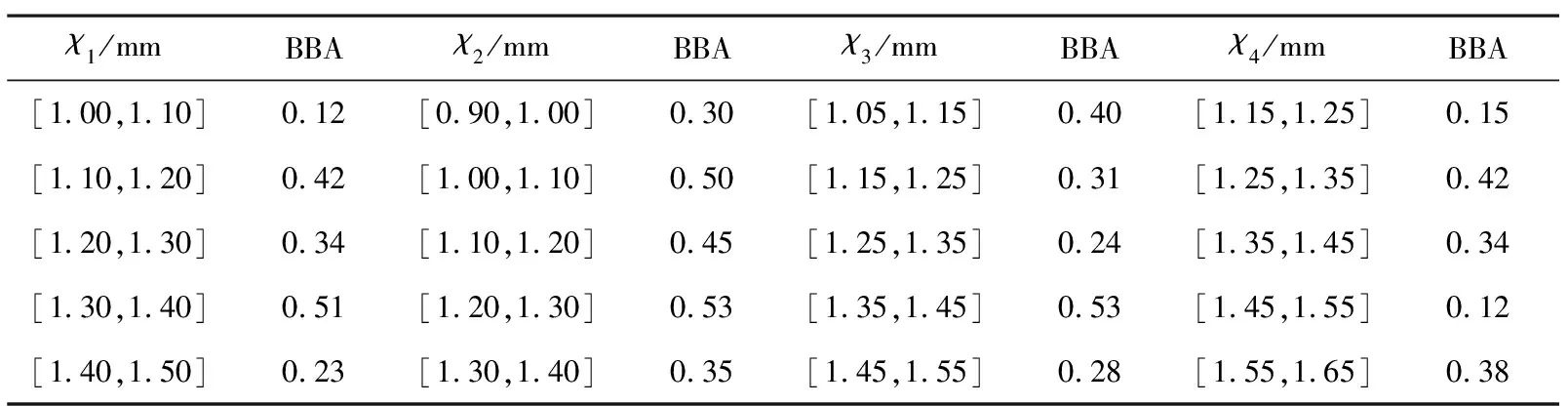
表1 设计变量基本信度分配BBA

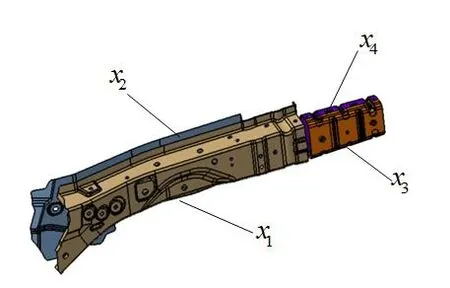
图5 设计变量分布图

3.2 可靠性区间分析

考虑到优化拉丁立方试验设计的约束随机性，且采样均衡、效率高的优点。故运用优化拉丁立方设计，选取了24个样本点，同时借助有限元模型进行仿真计算分析，在此基础上分析得出防火墙最大侵入量d的响应面函数[11]如下：

d(χ1,χ2,χ3,χ4)=

400.1435-17.6624χ1+21.4324χ2+5.1673χ3

-6.9624χ4-15.4252χ12+13.4234χ22+6.3323χ32+

1.5243χ42+3.5345χ1χ2-0.3423χ1χ3-21.3431χ1χ4-

6.9834χ2χ3+23.5345χ2χ4-13.5442χ3χ4

(5)

此偏置碰工况下，防火墙最大允许侵入量设定为dmax=240mm，据此建立如下确定性优化的边界数学表达式[12]：

(6)

其中g为整车左B柱下方最大加速度。经有限元仿真计算分析，得出的设计变量和结果表明变量χ2和χ4之间具有明显的相关性，再利用Copula函数结合可信度区间联合进行可靠性分析，进一步获得其可靠性区间为[0.431,0.768]。可见，车身前段结构中纵梁和吸能盒在此偏置碰工况下失效概率风险较大，防火墙最大侵入量仿真结果如图6所示。

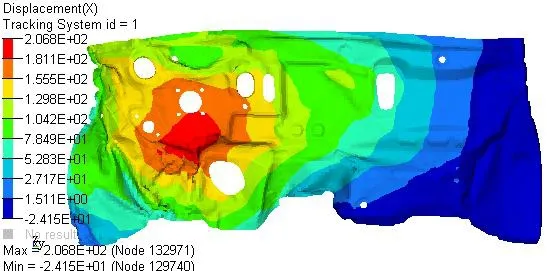
图6 防火墙侵入量分布图

4 结 论

(1)将Copula函数引入偏置碰撞优化设计，充分考虑分析结构设计部件间的相关性、设计变量不确定性导致的设计结果不可靠问题。

(2)研究发现偏置碰工况下，前纵梁内板厚度与前吸能盒内板的厚度具有明显相关性，变量间的相关性对可靠性分析结果影响较大。

(3)Copula函数可靠性结构优化，可广泛应用于设计变量的不确定性导致的设计结果不可靠问题。