保偏负曲率光纤的双折射特性分析

张正雄,陈吴,佟亮,代问问,刘韶清,郑子其,叶珊珊,王洋洋,蒋文辉,高伟清

(合肥工业大学电子科学与应用物理学院光学工程系,安徽 合肥 230601)

0 引言

1998年,Russell研究组[1]率先拉制出了第一根空芯光子带隙光纤(HC-PBGF)。相比于实芯的光子晶体光纤,HC-PBGF在材料吸收、色散、损耗和损伤阈值等方面都有突出的性能。但HC-PBGF严格的周期排布导致其设计自由度小,并且只能在特定的波长范围内进行传输。近年来,空芯负曲率光纤(HC-NCF)的出现引起了科研人员的广泛关注。与HC-PBGF不同,HC-NCF的结构没有严格的周期性排列,其结构简单、传输的带宽大、包层设计更为灵活[2],在紫外至中红外波段的激光传输中有广泛的应用前景[3]。关于HC-NCF的报道最早可追溯到2002年,Benabid等[2]报道了一种新型的Kagome空芯光纤。通过对Kagome光纤不断深入的研究,2011年,Pryamikov等[4]报道了一种由8个相邻圆环组成的HC-NCF。2013年,Yu等[5]提出并制备了在2.4µm损耗为24.4 dB/m的HC-NCF。为了研究HC-NCF的宽波段传输,同年,Kolyadin等[6]提出了能覆盖2.5∼7.9µm波段的HC-NCF。2017年,Debord等[7]制备出的HC-NCF在750 nm处的损耗低至7.7 dB/km,进一步阐述了HC-NCF的低损耗特性。2018年,Gao等[8]提出了一种连体管的HC-NCF,对比普通的HC-NCF,这种连体管进一步优化了HC-NCF的损耗,在1512 nm处的损耗低至2 dB/km。随后,英国南安普顿大学拉制出在C波段和L波段损耗为0.65 dB/km的HC-NCF[9]。2020年,南安普顿大学优化了光纤结构,拉制出在C波段和L波段损耗为0.28 dB/km的嵌套HC-NCF,这是目前报道损耗最低的HC-NCF[10]。

光入射到具有各向异性的晶体时通常会分解成两个正交偏振光,其传播速度和折射率一般都不相同,称为双折射效应。光在光纤中传输时容易受到外界因素如应力和温度等方面的影响,导致不可控的双折射,影响了光纤在各方面的应用。保偏光纤可通过改变光纤结构引入高双折射来减少外界因素的影响。对于传统的实芯光纤来说,主要通过改变纤芯的形状和光纤横截面的不均匀性来实现高双折射[11],如熊猫光纤。相比于实芯光纤,空芯光纤具有低色散、低非线性和高损伤阈值等方面的优势,所以,保偏空芯光纤在高功率激光传输等领域有更广泛的应用。2002年,Saitoh等[12]首次将改变形状导致双折射的方法应用到空芯光子晶体带隙型光纤中,数值模拟的双折射高达10−3,但光纤的损耗较大。2008年,Mangan等[13]拉制了一种保偏空芯光子带隙光纤,最低损耗为15 dB/km,双折射达到10−4。虽然光子带隙光纤能在空气中进行纤芯模式传输,但是导光通带窄和模式纯度差等缺点制约了其在光传输和光通信等方面的应用。而空芯HC-NCF弥补了空芯光子带隙光纤在导光通带和模式纯度方面的缺陷。2013年,Vincetti等[14]研究了纤芯椭圆率对空芯HC-NCF双折射特性的影响,但双折射都不超过7×10−5。2016年,Mousavi等[15]展示了一种在1550 nm处偏振消光比为1000的保偏HC-NCF。2018年,Wei等[16]提出一种在简单结构的无节点HC-NCF中引入双折射的方法,最终获得1550 nm处双折射为1.3×10−5。

目前为止,有关HC-NCF保偏和单偏振传输的研究还较少,主要集中在降低HC-NCF的损耗。目前所报道的负曲率保偏光纤的双折射和模间损耗比都还难以达到正常光纤的水平。本文提出一种新的HC-NCF结构,通过引入横向内包层破坏光纤的对称性,从而获得高双折射和高消光比。在引入内包层后,分析了影响光纤双折射和消光比的因素,包括内包层管的壁厚、直径和纤芯直径。通过优化光纤参数,模拟了该光纤在C波段传输时的双折射和消光比特性。结果表明,该光纤在1.55µm附近具有高双折射和高消光比,且满足低损耗传输。

1 HC-NCF双折射的物理模型和基本理论

1.1 有限元法

有限元法是一种用于求解各种物理场的计算方法,具体方程可表示为

式中:µr和εr分别表示介质磁导率和相对介电常数,E表示电场,ω表示真空中传播的频率,c表示真空中的光速。其思想是将连续求解域划分为多个相互独立的网格,再对这些离散的互联微小网格近似求解,最后获得整个区域的最终结果。这种方法计算精度高,适用于研究HC-NCF这种具有复杂结构的电磁场行为。另外,有限元算法的优势是对求解域网格划分比较灵活,可以自由控制求解域网格的疏密程度。一般情况下,对光场分布比较集中、结构曲率半径较小和折射率发生变化的位置进行网格细化,而其他位置可采用比较稀疏的网格。这种计算方法既提高了计算的准确性,又减少了计算量。

1.2 保偏HC-NCF模型的建立与基本原理

所设计HC-NCF的结构如图1所示,灰色区域代表空气。最外层黑色区域为完美匹配层(PML),其目的是为了减小模拟窗口的尺寸以及提高计算精度,厚度设置为设计波长的一半[17]。和PML相邻的区域为保护层,主要作用是保护光纤。光纤外包层由六个管环构成,管环的厚度为t,紫色部分代表石英材料;外包层管的内直径dtube由空气填充,其间距为g。纤芯直径为Dcore。Dcore可以表示为[18]

图1 所设计光纤的结构Fig.1 Structure of the designed optical f iber

式中p=6,表示环的数量。为了引入高双折射,添加了内包层,其由两个管环组成,管环的厚度为t1,橙色部分代表石英玻璃,内包层管的内直径为dtube1。由(2)式可得

主要适用于外包层环数量为6的情况。利用有限元算法分析HC-NCF的模场特性以及损耗特性。

没有引入内包层情况下,当满足反谐振条件时,外包层管环壁厚t表示为[19]

式中:λ为波长,n1和n0分别为石英玻璃和空气的折射率,m为任意正整数。光在传输时共有三种模式:材料中的玻璃管模式,包层环内空气部分的包层管模式和纤芯模式。在满足反谐振条件时光会从玻璃管中反射回纤芯,减少纤芯模式的泄露。因此,为了减少纤芯模式泄漏,包层管的壁厚应该满足反谐振条件。在空芯HC-NCF中,每一个单独包层环也具备反谐振条件,可以把模式束缚在环中,导致外包层空气中的管模有效折射率和纤芯中有效折射率几乎一致,这会使纤芯基模和空气中的管模发生耦合,导致纤芯的损耗增大。为了抑制两个模式的耦合,需要使两个模式之间有一定程度的空间错位,并且使两个模式的有效折射率失配[20]。这就要求在设计空芯HC-NCF时,既要满足壁厚t的反谐振条件来防止纤芯模式泄露,又要考虑纤芯和外包层管的内直径大小来抑制纤芯模式和外包层空气中的管模的耦合。所以,通过引入横向内包层改变结构对称性的方法来提高双折射。在引入内包层后,既破坏了光纤的对称性,又减少了外包层管和纤芯之间的模式耦合。光纤双折射B可表示为

式中:βx、βy分别表示x和y两个正交方向上的模式传播常数,nx、ny表示两个正交方向的有效折射率。在引入内包层时,随着内包层管壁厚度的变化,纤芯模式和玻璃管模式发生反交叉式的耦合现象。两种模式的耦合将局域改变其有效折射率。另外,这种模式耦合还会在光纤的损耗谱内引入一个损耗尖峰[21]。通过这种方式可以获得具有高双折射和具有单偏振传输特性的光纤,其中偏振消光比(PER)[22]定义为两个正交方向上的基模损耗比值,当PER大于100(20 dB)时,则可认为是单偏振光传输。当然在获得高折射率保偏光纤的同时,需要保证光纤的限制损耗不能过高。限制损耗LC可以表示为[23]

式中:nimag表示有效折射率的虚部,λ表示光的波长。

2 HC-NCF参数对传输特性的影响

2.1 壁厚t和包层管直径d tube1对光纤双折射的影响

本节主要讨论引入内包层后,内包层管环壁厚和内包层管的内直径对光纤双折射和损耗的影响。外包层管环壁厚和外包层管内直径的大小主要是控制光纤的损耗,对光纤的双折射影响不大。设计波长为1550 nm,玻璃材料折射率为1.444。为了不增大光纤限制损耗,同时考虑光纤制备的简易性,选择外包层管壁厚t在二阶反谐振区。根据(4)式可知,当m=2时,壁厚为1.116µm。纤芯直径Dcore和外包层管的内直径dtube都为30µm。以下计算都设置外包层管的内直径和纤芯直径的值相等。首先,对内包层管环壁厚t1进行分析。内包层管的内直径dtube1是外包层管的内直径dtube的一半。图2所示为x和y偏振分量有效折射率随内包层管壁厚变化的曲线图。由图2可知,x和y偏振分量的有效折射率相差不大。但在内包层管壁厚为0.8µm和1.55µm时x和y偏振分量的有效折射率出现了不连续的情况,这是因为光传输时在这两个位置发生了一阶和二阶谐振,光不能透过。另外,当内包层壁厚接近谐振壁厚时,x和y偏振分量的有效折射差会变大。当内包层管环壁厚在一阶谐振附近(0.8µm)时,x和y偏振分量的有效折射率差为1.9×10−5;当壁厚在二阶谐振附近(1.55µm)时,x和y偏振分量的有效折射率差为2.33×10−5。所以,对于该结构的保偏HC-NCF来说,内包层管环壁厚应选择在谐振区域附近,以下研究中选择内包层管环壁厚在二阶谐振附近进行分析。

图2 x和y偏振分量有效折射率随内包层壁厚变化曲线Fig.2 Variation curve of x and y polarization effective refractive index with inner cladding wall thickness

分析了内包层管环壁厚对光纤双折射的影响后,需要研究内包层管的内直径对光纤双折射特性的影响。为了保证光能传输,内包层管环壁厚选取在二阶谐振附近,其余的参数不变,即t1=1.56µm,使内包层管的内直径在6∼29µm内变化。图3为双折射随内包层管内直径变化的曲线。该光纤结构的双折射会随着内包层管内直径的增大呈现出先上升后下降的趋势。在内包层管的内直径为8µm和9µm时,光纤的双折射都超过了10−4。当光纤内包层管的内直径超过这两个值时,双折射会下降。当内包层管的内直径增大到17µm以后,该光纤的双折射低于10−5。所以,对于纤芯直径为30µm的情况,选择内包层管的内直径为9µm。

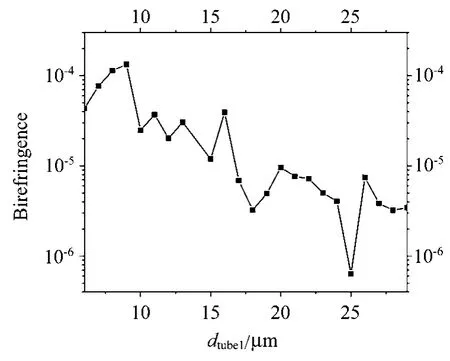
图3 双折射随内包层管环的内直径变化曲线Fig.3 Variation curve of birefringence with inner cladding tube diameter

以上研究表明,当壁厚值接近谐振区域时光纤具有高双折射,但HC-NCF对内包层管壁厚值较为敏感。所以,选择内包层管的内直径为9µm时,在接近二阶谐振区域做进一步分析。图4(a)所示为x和y偏振分量有效折射率随内包层管壁厚增大的变化趋势。当内包层管壁厚增大时,x偏振分量分别在壁厚值为1.56µm和1.59µm处有效折射率发生突变,而y偏振分量分别在1.56µm和1.58µm两个位置发生突变。这是因为在引入内包层时,两个正交方向上的模式和内包层玻璃管模式进行耦合。图4(b)所示为双折射随内包层管壁厚变化的曲线图。与有效折射率变化趋势相对应,当基模的x和y偏振分量与玻璃管模式发生耦合时,光纤的双折射都会出现峰值。其中当壁厚值t1=1.56µm时,双折射值最大,B=1.33×10−4。图4(c)所示为x和y偏振分量的损耗随内包层壁厚变化的曲线图。由图可见x偏振的损耗都大于1 dB/m,在横向引入内包层,所以对x偏振分量的耦合更明显。x偏振和y偏振在耦合的位置都出现了损耗增大的现象。由于内包层的引入,两个正交方向上的基模与包层玻璃管模式发生耦合后会泄露到包层中,导致模式的损耗增大。图4(d)所示为x和y偏振分量偏振消光比随内包层管壁厚变化的曲线图。在t1值为1.55∼1.562µm、1.593∼1.6µm范围时,偏振消光比都大于100(20 dB),其中在t1=1.56µm时,偏振消光比最大,达到了4723(36.7 dB)。

图4 纤芯直径为30µm。(a)有效折射率随内包层壁厚变化曲线;(b)双折射随内包层壁厚变化曲线;(c)损耗随内包层壁厚变化曲线;(d)PER随内包层壁厚变化曲线Fig.4 The core diameter is 30µm.(a)Variation curve of effective refractive index with inner cladding wall thickness;(b)Variation curve of birefringence with inner cladding wall thickness;(c)Variation curve of loss with inner cladding wall thickness;(d)Variation curveof PER with inner cladding wall thickness

2.2 纤芯直径对光纤双折射的影响

根据Marcatili和Schmeltzer模式传输理论[24],当增大纤芯直径时,入射光在纤芯边界的掠射角会增大,从而提高了菲涅尔衍射,所以可以通过增大纤芯直径来减少模式的传输损耗。两个正交方向上的损耗都会降低,这也将影响光纤PER的值和双折射。为了研究纤芯直径对该HC-NCF双折射特性的影响,分别选择了纤芯直径为20µm和40µm进行计算。虽然改变纤芯直径的大小并不会影响传输时的边界值,但HC-NCF的光传输由反谐振和模式耦合共同决定,所以内包层管的内直径值会影响光纤的双折射特性。此时固定内包层管壁厚的大小为1.56µm。图5(a)、(b)分别表示纤芯直径为20µm、40µm时,光纤双折射随内包层管的内直径变化的趋势。它们都在dtube1=8µm时,双折射值达到最大,分别为1.74×10−4和7.2×10−5。这说明在同样的条件下,增大纤芯直径会降低双折射的值。

除了内包层管的内直径大小,壁厚对双折射也有影响。纤芯直径为20µm、内包层管的内直径为8µm时,光纤的双折射特性以及PER随内包层管壁厚的变化趋势如图6所示。与图4相比,两种情形下纤芯模式都会与玻璃管模式发生耦合从而使有效折射率不连续。当纤芯直径减小时,光纤的高双折射所对应的壁厚位置和大小都会发生变化。纤芯直径为20µm时,在壁厚值为1.566µm时双折射值和PER值都达到最高,分别为2.62×10−4和234(23.7 dB)。但是,纤芯直径的大小影响传输损耗,此时y偏振的损耗约为0.8 dB/m,增大了一个数量级。

图6 纤芯直径为20µm。(a)有效折射率随内包层壁厚变化曲线;(b)双折射随内包层壁厚变化曲线;(c)损耗随内包层壁厚变化曲线;(d)PER随内包层壁厚变化曲线Fig.6 The core diameter is 20µm.(a)Variation curve of effective refractive index with inner cladding wall thickness;(b)Variation curve of birefringence with inner cladding wall thickness;(c)Variation curve of loss with inner cladding wall thickness;(d)Variation curve of PER with inner cladding wall thickness

纤芯直径增大到40µm时,x和y偏振分量有效折射率随内包层管壁厚变化的曲线如图7(a)所示。与纤芯直径30µm相比,x和y偏振分量的耦合位置不一样,内包层管壁厚分别为1.572µm和1.578µm。图7(b)所示为双折射随内包层管壁厚变化的曲线图。当纤芯直径增大时,光纤的双折射会下降,都低于10−4。当光纤的壁厚值为1.56µm时,光纤具有最大的双折射值7.48×10−5,其对应的PER为163(22.1 dB)。图7(c)所示为损耗随内包层管壁厚变化的曲线图。虽然双折射值降低,但是随着光纤直径的增大,光纤整体的传输损耗也降低了,在t1为1.71µm时光纤的传输损耗约为9×10−3dB/m。图7(d)所示为x和y偏振分量的偏振消光比随内包层壁厚变化的曲线图。在壁厚值为1.56∼1.574µm都能保证单偏振光传输,其中在1.71µm处具有最大的PER,为1.6×104(42.04 dB)。

图7 纤芯直径为40µm。(a)有效折射率随内包层壁厚变化曲线;(b)双折射随内包层壁厚变化曲线;(c)损耗随内包层壁厚变化曲线;(d)PER随内包层壁厚变化曲线Fig.7 The core diameter is 40µm.(a)Variation curve of effective refractive index with inner cladding wall thickness;(b)Variation curve of birefringence with inner cladding wall thickness;(c)Variation curve of loss with inner cladding wall thickness;(d)Variation curve of PER with inner cladding wall thickness

因此,纤芯直径小于30µm时,虽然会增大光纤的双折射,但同时也会增大光纤的传输损耗,且光纤的偏振消光比也会随之变小;当光纤大于30µm时,传输损耗会下降,偏振消光比会得到大幅度上升,但双折射会下降,都不会超过10−4。另外,当纤芯直径过大时,还会产生高阶膜,导致模式不纯。为了获得高双折射、低损耗以及高消光比的光纤,纤芯直径选定为30µm。

2.3 优化后1.55µm附近的双折射

在分析了内包层的壁厚、直径以及纤芯对光纤双折射的影响后,确定了光纤结构参数,如表1所示。

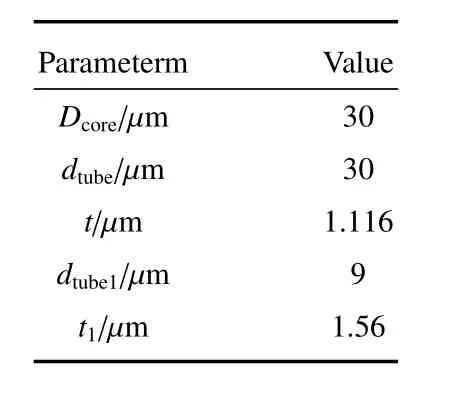
表1 光纤结构参数Table 1 Optical fiber structure parameters

在明确光纤的参数后,进一步分析了该光纤结构在C波段的双折射特性。如图8(a)所示为x和y偏振分量随波长变化的曲线图,该光纤结构在波长大于1.545µm的双折射都大于10−5,这是因为在1.544µm处y方向上的偏振与玻璃管模式发生耦合导致有效折射率发生突变,损耗也随之升高。从图8(b)可以看出,在1.549∼1.55µm和1.556∼1.56µm的双折射都在10−4左右,在1.55µm的双折射为1.33×10−4。如图8(c)所示为损耗随波长变化的曲线图,当波长大于1.546µm时,y偏振分量损耗都小于1 dB/m,在1.55µm处的损耗约为0.03 dB/m。图8(d)为偏振消光比随波长变化的曲线图,在1.547∼1.554µm的7 nm范围内偏振消光比都大于100(20 dB),偏振消光比在1.55µm附近达到6684(38.3 dB)。

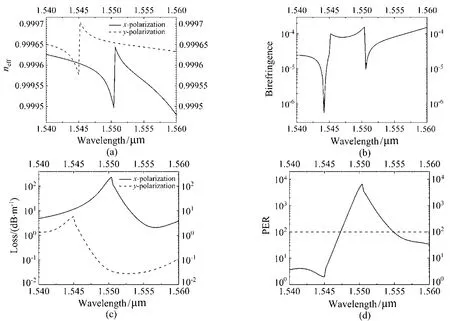
图8 (a)有效折射率随波长变化曲线;(b)双折射随波长变化曲线;(c)损耗随波长变化曲线;(d)PER随波长变化曲线Fig.8 (a)Variation curve of effective refractive index with wavelength;(b)Variation curve of birefringence with wavelength;(c)Variation curve of loss with wavelength;(d)Variation curve of PER with wavelength

3 结论

通过引入横向内包层破坏光纤结构的对称性,利用纤芯模式和内包层的玻璃管模式的反交叉耦合来提高HC-NCF的双折射和消光比,并研究分析影响光纤双折射和消光比的因素,包括内包层管壁厚、内包层管的内直径和纤芯直径。对光纤结构优化后,进一步分析该光纤结构在C波段的双折射特性。最终,在1.55µm波长处的双折射达到1.33×10−4,偏振消光比达到4723(36.7 dB),最低损耗约为0.03 dB/m,并且可实现带宽为7 nm的偏振滤波。本工作将为空心光纤中偏振敏感器件提供有效的解决办法。