三角形截面GaN纳米线中的Fröhlich电子-声子相互作用哈密顿

张 立,王 琦

(1广州番禺职业技术学院智能制造学院,广东 番禺 511483;2北京大学东莞光电研究院,广东 东莞 523429)

0 Introduction

Nitride semiconductor materials including GaN, AlN and their ternary alloy Al GaN and In GaN have continually attracted much attention during last two decades due to their excellent optical and electronics properties,such as wide and adjustable band-gap, strong atomic bond and high thermal stability. These characteristics result in their great potentials on the ultra-fast and super-stability hotoelectron components and devices. Since the pioneering work of fabricating nitride nanowire with circle cross-section[[1],a serious of GaN-based nanowires with different cross-sections,such asrectangular cross-section[2],hexagonal cross-section[3]and triangular crosssection[4],have been grown and synthesized based on the advanced MBE and MOCVD technique.It is well known that a quanta of crystal-lattice oscillation,also called phonon,is one type of important and typical elementary excitation in solid.The phonons in crystal affect greatly not only the transport of carriers,but also the optic and optoelectronic properties,such aselectron-phonon scattering,hot electron relaxation,interband transition and exciton lifetime[5,6].Furthermore, both theories and experiments reveal that, not only the electronic and optical features, but also the polar phonon states and their interactions with carriers are influenced greatly by the shape and size of cross-sections[7−9].Although some phonon modes and their corresponding electron-phonon interactions in GaN-based nanowires with circle cross-section and rectangular cross-section have been studied[8,9],the polar optical phonon modes in GaN-based nanowires with triangular cross-section havenotbeen investigated and fully understood to the best of our knowledge by now.Hence it is necessary and meaningful to investigate the crystal-lattice dynamic in wurtzite nitride nanowires with triangular cross-section.

In fact,the math and physical problems of an equilateral triangle attracted great attention more than forty years ago.For example,Li and Blinder[10,11]derived the exact solutions of the Schrödinger equation for a particle in an equilateral triangle by use of projection operators and nonseparable variables approach.Pinsky[12]discussed the eigenvalues of an equilateral triangle,both the Dirichlet and Neumann boundary conditions were considered.McCartin[13,14]analyzed the eigenvalues and eigenfunctions of the Laplacian with Dirichlet boundary conditions and Neumann boundary conditions on an equilateral triangle by using direct elementary mathematical techniques. The results show that the eigenfunctions form a complete orthogonal system. Pr´aha[15,16]investigated the eigenvalues and eigenfunctions of the Laplace operator on an equilateral triangle based on an approach of transforming problem of an equilateral triangle into that of a rectangle.Freitas[17]proved some new upper and lower bounds for the first Dirichlet eigenvalue of a triangle in terms of the lengths of its sides.

IIn the present paper, we will investigate a phonon modes in GaN nanowire with quilateral triangular crosssection in vacuum for simplicity.The main significance of the work embodies the following four points.First,it is predicted that the exactly confined(EC)phonon modes can appear in the nitride nanowire system,and the characteristic frequency(ωz,L)of ECmodesispointed out,which is obviously different from the case of wurtzite quantum well(QWs)systems[18]due to their different conf ined dimensions(In wurtzite QWs,the characteristic frequency of ECmodesisωt,L).Secondly,the exact and analytical phonon states of ECmodesin the anisotropic wurtzite nanowires with equilateral triangular cross-section have been given based on the dielectric continuum model.Thirdly,the polarization eigenvectors and their orthogonality relations for the EC phonon modes are derived,which could form a set of orthogonal and completed basis vectors.And the free phonon fields and the corresponding Fröhlich electron-phonon interaction Hamiltonian areobtained based on orthogonality relation of polarization eigenvectors and field quantization method.Finally,the electron-phonon coupling functions for ECmodes are numerically discussed,and relative properties and conclusions are derived.

1 Theory

Let us consider a wurtzite GaNNW with equilateral triangular cross-section located in vacuum(refer to Fig.1).Thez-axis is taken along the direction of thec-axis of the wurtzite material,and thex-axis(y-axis)is taken along(perpendicular to)the direction of oneside of equilateral triangle.Dueto theanisotropy of wurtzitecrystal,the dielectric functionεbecomes direction dependent.Considering the isotropy inx-direction andy-direction,onecan writeεx=εy=εt.Thusεisgiven by

Fig.1 Schematic view of the model of wurtzite GaN nanowires with equilateral triangular cross-section

where

As discussing in our previous works[8,9],it can be confirmed that there are five distinct types of phonon modes including interface optical(IO)modes,half space(HS)modes,propagating(PR)modes,quasi-confined(QC)modes and EC modes in wurtzite nitride quantum systems.Shi[18]pointed out that,due to the anisotropy of structure,the EC modes of wurtzite quantum structures usually can not be strictly confined in someone materiallayer.But if the phonon frequencyωapproaches the characteristic frequenciesων,L(ων,Lis the frequency of longitudinal-optical(LO)phonon inν-direction,ν=t,z),the electric potential of EC phonons nearly can be confined in one material-layer.Namely,the electrostatic potentials of EC modes are strictly confined to someone wurtzite material,and will disappear at the interfaces of the quantum structure.The situations are very similar to the bound electron states in quantum structures with infinite potential[8,18].In fact,the EC modes can be obtained from the QC modes in the limit ofωEC→ων,L.

1.1 Analytical phonon states of EC modes

On the basis of the single particle states in equilateral triangle quantum systems[10,11],we can write the phonon potential of EC modes in wurtzite nanowires with equilateral triangle cross-section as

with symmetric solutions

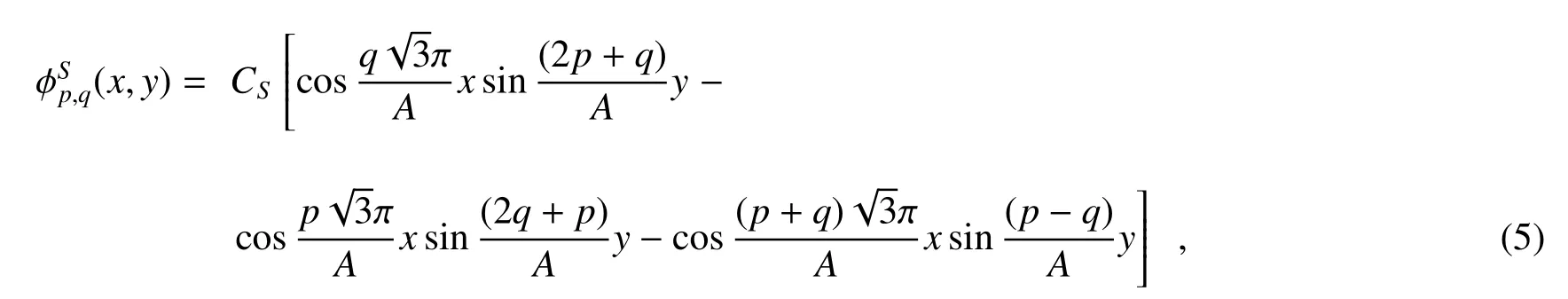
and anti-symmetric solutions

wherekzis the wave-number of EC modes in freez-direction,Ais the altitude of the equilateral triangular crosssection,CSandCAare the normalization constants determined by Eq.(16),andp,qare quantum numbers which are a serial of integers satisfied the relationshipq=0,1,2,···,p=q+1,q+2,q+3,···

1.2 Orthogonality relation of polareigen-vectors for EC modes

In order to obtain the analytical electron-phonon interaction Hamiltonian of ECmodes in the structures,let us discuss the orthogonality of polar eigen-vector of EC modes.The polarization fields of the symmetrical EC phonon modes in the system are given by

The polarization fields of the anti-symmetric EC phonon modes are given by

In theabove Eqs.(7)and(8),ex,eyandezdenote the unit vectors inx−,y−andz-direction,respectively.Using the orthogonality of the sine and cosine functions,we can obtain the following orthogonality relation for the polarization eigenvectoras

In Eq(9),Lzdenotes the length of the wurtzite nanowires inz-direction.

1.3 Fröhlich electron-phonon interaction Hamiltonian for EC modes

In order to derive the free EC phonon Hamiltonian in the system,the dynamic equation of motion of the wurtzite crystal latticecan bewritten as

Moreover,the polarization vector can be written as

whereµis the reduced mass of the ion pair,uis the relative displacement of the positive and negative ions,n∗is the number of ion pairs per unit volume,ω0tandω0zare the frequency associated with the short-range force between ions,αtandαzare the electronic polarizability per ion pair,andare the effective charges of the ions,andEloc,tandEloc,zarethelocal f ield at theposition of the ionsalong thetandzdirections,respectively.

The Hamiltonian of the free vibration in wurtzite crystal can be written as

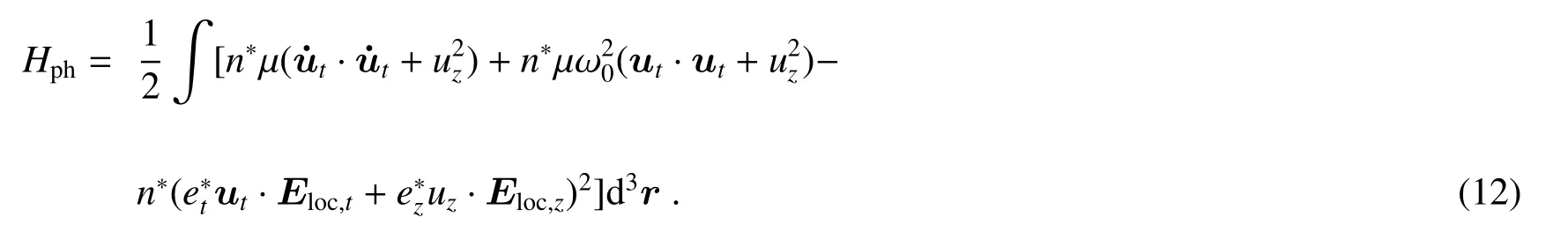
Making use of the well-known Lorentz relationEloc=E+4πP/3[19],we have

and

Substituting Eqs.(13)and(14)into(12),we can writethe ECphonon Hamiltonian as

If we choose the coefficientCS/Ato be

The operators for the (kz,p,q)EC phonon modes satisfy the commutation relation for bosons. The eigenfunction of the EC phonon modes Φ(r)could be expanded in terms of the normal modes, so the Fröhlich Hamiltonian between the electron and EC phonon is obtained as

where

with

It should be noted that the static and high-frequency dielectric constants of GaN bulk material int-andzdirections are almost the same,so they are not distinguished in Eq.(20).

2 Results and discussion

In order to see more clearly the distributions of phonon potential and strength of electron-phonon coupling for the EC modes in the nitride nanowires with triangular cross-section, the numerical calculation on the function Γkz,p,q(x,y)is performed for a wurtzite GaN nanowire. The material parameters used in the calculations are listed in Table 1.(x,y)[in 10−8(meV C2nm−1)−1/2]as functions of the coordinatesxandyare plotted in Fig.2 when the wave-numberkzis kept as1/A,the quantum-numberqis fixed on 0 and another quantum-numberpequals1,2,3,4,respectively.The side length of the GaN nanowire is chose to be6 nm.From the figure,it is seen that the electrostatic potential of the EC modes are strictly confined in the triangular ranges of the GaN nanowire.Furthermore,if one uses a plane which is parallel to the side of the triangle and the axis line of the nano wire(i.e.thez-axis)to cut into the two-dimensional curved surfaces,the section lines obtained are obviously symmetrical.This just explains the reason why these EC modes are called as symmetric phonon modes.From Fig.1(a),it is found that only one peak appears,which means that it is the ground-state phonon potentials of EC modes asp=1 andq=0.With the increase ofp[see Fig.1(b)-(d)],the

Fig.2 Symmetrical electron-phonon coupling function (x,y)[in 10−8(meV·C2·nm−1)−1/2]as functions of the coordinates x and y.(a)p=1,q=0;(b)p=2,q=0;(c)p=3,q=0;(d)p=4,q=0

Table 1 Zone-center energies(in meV)of polar optical phonons,dielectric constants of wurtzite GaN material[18]

The symmetrical electron-phonon coupling function peaks and troughs of the function(x,y)also increase correspondingly.An interesting phenomenon is that,the peak number is larger than the trough number,and the total number of the peaks and trough of these curved surfaces is just the square of quantum numberp(i.e.p2).For example,in Fig.1(b),there are three peaks and one trough asp=2.So the total number of peaks and troughs are four,and it is just the square of quantum numberp=2,namelyp2=4.In Fig.1(c),the total number of peaks(six)and troughs(three)is nine,and that is just the square of the quantum numberp=3,i.e.p2=9.On the other hand,the absolute values of peaks and troughs of(x,y)become smaller and smaller as quantum numberpincreases.This reveals that the coupling strengthen of electron-phonon interaction of the high-order ECmodes is weaker than that of the low-order ones.

The anti-symmetrical electron-phonon coupling function(x,y)[in 10−8(meV·C2·nm−1)−1/2]asfunctions of the coordinatesxandyare displayed in Fig.3 when the wave-numberkzis kept as 1/A,the quantumnumberqis f ixed on 1 and another quantum-numberpequals 2,3,4,5,respectively.The side length of the GaN nanowire is chose to 6 nm.In the same way,the anti-symmetrical coupling functions(x,y)are also rigorously bounded in the equilateral triangular range.As one uses a plane which is parallel to one side of the triangle and thez-axisline of the nanowire to cut into the two-dimensional curved surfaces,the section lines obtained areobviously anti-symmetrical.Thisobservation isillustrated that the reason why these ECmodesare called asanti-symmetric phonon modes.For certainpandq,the peak number of the anti-symmetrical coupling functionsisequal to thetrough one.For example,both thepeak number and thetrough number aresix asp=3 andq=1 in Fig.3(b),and both the peak number and trough number are 9 asp=4 andq=1 in Fig.3(c).The phenomenon that the coupling strengthen of electron-phonon interaction become weaker and weaker asthe quantum numbersporqin creasesisobserved again.

Fig.3 Anti-symmetrical electron-phonon coupling function(x,y)[in 10−8(meV·C2·nm−1)−1/2]as functions of x and y.(a)p=2,q=1;(b)p=3,q=1;(c)p=4,q=1;(d)p=5,q=1

Next let us brief ly discuss the quantum size effect on the electron-phonon coupling function of EC modes.Fig.4 plotsthe electron-phonon coupling function(x,y)[in 10−8(meV·C2·nm−1)−1/2]as functions of the coordinatesxandyfor the lowest-order symmetrical ECmodes withp=1 andq=0.The freewave-numberkzis mixed at 0.5×109m−1.Four different sizes of equilateral trianglecross-section of nanowires[namely the side lengthL=1 nm(a),L=20 nm(b),L=50 nm(c),L=100 nm(d)]are selected.From the figures,it is seen that the strength of electron-phonon coupling decrease obviously with the in crease of the side length of nanowire cross-section.Comparing the four figures,it is found that,as the side lengthsLincrease from 1 nm to 100 nm,the maximum values of coupling strength nearly decrease to be one fourth of the first one.

Fig.4 Electron-phonon coupling function(x,y)[in 10−8(meV·C2·nm−1)−1/2]asfunctions of the coordinates x and y for the lowest-order symmetrical ECmodes.(a)L=1 nm;(b)L=20 nm;(c)L=50 nm;(d)L=100 nm

Similar to Fig.4,the electron-phonon coupling functions[in 10−8(meV·C2·nm−1)−1/2]as functions of the coordinatesxandyare plotted in Fig.5 for the symmetrical ECmodes withp=2 andq=0.The free wave-numberkzinz-direction is mixed at 0.5×109m−1.Also four different sizes of equilateral triangle cross-section of nanowires[namely the side lengthL=1 nm(a),L=20 nm(b),L=50 nm(c),L=100 nm(d)]are chosen.Similarly,it is also observed that the strength of electron-phonon coupling become weaker and weaker with the in crease of side length of nanowire cross-section.Moreover,as the side lengthsLdecrease from 100 nm to 1 nm,the maximum values of coupling strength nearly increase to be four times of the first one.

3 Summary

In summary,the polar optical phonon states of a wurtzite nitride nanowire with equilateral triangle crosssection are investigated for the first time in the present paper.The exact and analytical phonon states of EC modes are obtained based on the dielectric continuum model.The characteristic frequency of EC modes in the nanowire structures,namely the frequency of longitudinal optical phonons inz-directionωz,Lis specif ied,which is obviously different from the situation of the EC modes in wurtzite QW system[18]due to their different conf inement and dimensions.In GaN-based QWs,the characteristic frequency of EC modes is the frequency of longitudinal optical phonons in freet-directionωt,L.Furthermore,the polarization eigenvectors and their orthogonality relations for the EC phonon modes in the systems are derived,and these polarization eigenvectors could form a set of orthogonal and completed basis vectors.Moreover,by using the orthogonality relation of polarization eigenvectors and the usual f ield quantization method,the free phonon f ields and the corresponding Fröhlich electron-phonon interaction Hamiltonian are obtained.Numerical calculationson a GaN nanowire with trianglecross-section are per formed.The electron-phonon coupling functions of the symmetrical ECmodes and anti-symmetrical ones as functions of the coordinatesxandyare depicted.The potential of these EC phonon modes are strictly confined in the triangle ranges.And the symmetries and coupling strengthen are analyzed in detail.Relationship of the total number of peaks and troughs with the quantum numbers are discussed.The results obtained here are quite useful for the investigation of the electron-phonon scattering[5]and polaronic effect[20]in the wurtzite nanowire with triangle cross-section.