基于ICPSO-BP神经网络的光纤SPR传感器开环系统优化研究

付丽辉,戴峻峰

(1淮阴工学院自动化学院,江苏 淮安 223003;2淮阴工学院电子信息工程学院,江苏 淮安 223003)

0 引言

光纤表面等离子共振(SPR)传感器的开环结构具有简单、无需复杂的信号处理以实现闭环反馈之优点,但是在测量过程中,由于放弃了对SPR传感头共振吸收中心的锁定,其测量结果具有“开放性”,输出光电流相对于探测光中心频率有所偏离[1,2],而以调频光一阶边带处SPR吸收谱的一阶微分值为比例系数,当波长偏离程度提高时可以使分辨率培增,但由于SPR共振吸收机理的复杂性,导致光电流与波长偏离程度之间的线性难以保证,动态范围变窄,对应可测量折射率变化范围减小,系统性能劣化[3]。因此,如果没有相应措施以有效应对开环系统的上述弊端,光纤等离子共振传感器开环测试结构将不具有应用可行性。

目前,神经网络在众多已有非线性系统识别和校正中的应用效果,使其尤为适合SPR开环结构非线性校正的要求。人工神经网络是一种模拟人脑的算法,其主要特点是并行处理、分布式存储、运算速度快、具有较理想的容错性,同时,还具有自学习、自组织、自适应能力[4,5],这些结构特点使人工神经网络在非线性系统矫正方面具有很大的应用前景。随着对光纤SPR传感结构研究的进一步深入,对传感器的准确度、线性度等均有更高的要求,而神经网络所具有的良好非线性映射和逼近能力,使其非常适合SPR传感器开环测试结构的非线性校正应用。采用神经网络方法,不需要深入了解其内部结构就能很好地解决传感器的“黑箱问题”。因此,本文利用神经网络对SPR开环结构的非线性传感系统进行逆向建模,从而实现对其进行非线性补偿。

1 补偿原理

SPR开环检测结构对应的传递函数具有非线性,其反函数也为非线性。并且,在处理过程中很难精确获得这种非线性模型,必然影响其测量结果的准确度。另一方面,神经网络可以映射非线性函数,具有较强的推广和泛化能力,能够实现盲学习[5],通过选取少量样本让神经网络进行训练,即能映射该反函数,运用这一原理,在光纤SPR传感器开环测试系统输出后接入神经网络,可以实现对SPR传感器非线性失真的校正,以此消除SPR开环测试结构对传感器性能的影响,对应的非线性补偿原理如图1所示。

图1 SPR传感器神经网络补偿原理图Fig.1 Neural network compensation schematic diagram of SPRsensor

设被测介质折射率为n,SPR传感器输出值为u,神经网络输出值为y,则y能无限逼近n。其中,SPR传感器输出为u=f(n),开环SPR传感结构特点决定u为非线性函数;补偿环节输出为y=F(u),F(u)为补偿环境传递函数。

若使得F(u)=f−1(u),则

由此,测量值n与系统输出y相同,从而获得理想的传输特性。另一方面,F(u)为非线性函数,其表达式具有黑箱性,因此,本研究利用神经网络对其内部映射进行学习及训练,从而取代F(u)。

2 合作粒子群算法(ICPSO)优化的反向传播(BP)神经网络

目前,BP神经网络是一种比较成熟的神经网络,其局限性主要体现在:

1)基于保证网络的稳定性需求,常取较小的学习率,导致网络训练的收敛速度慢;

2)基于误差函数曲面的“凸凹不平”性以及BP算法采用的最速下降法—沿曲面下降方向滑向曲面某“谷底”,导致网络训练容易陷入局部极小点;

3)基于神经元所采用的S型激励函数自身特点,导致网络训练容易陷入S型函数的饱和区。

由此,众多学者提出了一些改进算法[6],但大多为局部搜索算法,其全局最优解及泛化能力经常无法保证。因此,本研究提出基于改进的粒子群算法优化的BP神经网络补偿模型。粒子群算法计算量小且具有全局优化能力,己被广泛地应用于各类离散及连续问题的参数优化中。

2.1 PSO及其改进

Kennedy和Eberhart于1995年首次提出粒子群算法(PSO),该算法初始化为一群随机粒子[7],通过迭代找到最优解。在每一次迭代中,粒子通过跟踪两个极值来更新自己,一个极值是粒子本身个体最好值,另一个极值就是整个种群寻优的全局最好值,每个粒子通过上述的两个极值不断更新自己,从而产生新一代的群体。其主要缺点是过分依赖全局最优信息导致其易陷入局部最优[8],主要原因为粒子早熟收敛,即粒子状态趋同,丧失其多样性。由此,人们进行了不同的改进和尝试[9,10],其中,比较常见的有调整加速度系数或权重的方法,但其调整过程具有较强随意性,优化能力有限;而划分子群的方法能够较好地克服粒子状态趋同问题,但子群信息权重的选择又成为新的隐患。为此,提出一种动态信息调整且速度可控的合作粒子群算法(ICPSO)。通过设定子群,引入子群最优信息并利用迭代次数来动态控制子群与全局最优信息的作用,以实现在寻优前期以全局最优信息引导为主,子群最优信息的作用会随着寻优过程的深入而逐渐提高,以此来保持粒子的多样性。

基本PSO算法中的粒子状态更新方程为[10]

式中:vt+1为第t+1次迭代中第i个粒子第m维速度,xt+1为其对应位置;pit为第i个粒子第t次迭代的自身最优值,pgt为其全局最优值;r1,r2是[0,1]间随机数;c1,c2是加速系数;ω是惯性因子。

ICPSO算法粒子状态更新可表示为

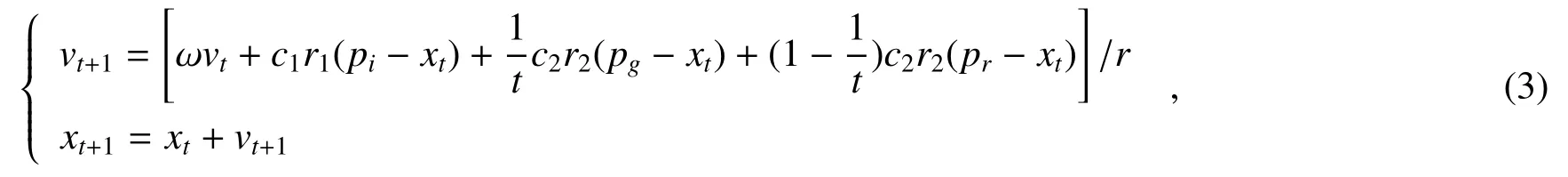
式中:r为子群数,pr为子群的最优值,其余各参数含义同(2)式。ICPSO算法的粒子移动过程如图2所示。

图2 ICPSO算法的粒子移动过程Fig.2 Particle moving process of ICPSO algorithm

由(3)式可见,粒子飞行速度更新迭代方程中增加了第四项,该项表征了子群最优信息对粒子寻优的影响,同时,第三及第四项中引入参数1/t和(1−1/t),用以动态调整全局及子群最优信息对粒子状态更新的影响,1/r则考虑分组数对寻优速度的影响。

当种群划分为r组后,在确定粒子状态时会考虑以下几个方面:子群最优与粒子当前位置间的方向pr,全局最优与粒子当前位置间的方向pg,自身最优与当前位置间的方向pi,当前速度vt。

在寻优中,粒子利用1/t和(1−1/t)因子动态调整全局最优、个体最优、子群最优的共享信息,具体地,当t值较小,寻优过程处于前期时,各粒子以全局最优为主要共享信息;当t值逐渐变大,迭代次数增加,子群最优值则为重要的共享信息,由此避免了粒子状态过早趋同,从而保证算法兼具更好的全局及局部寻优能力。另外,1/r系数用于收敛速度的控制,当r处于[1,∞]时,1/r则处于[0,1],由此可调整并达到与收敛精度更相适合的收敛速度,相应证明见文献[11]。

表征寻优算法质量的重要指标有寻优精度及收敛速度,应用中需综合平衡二者的关系。由(3)式综合分析可见,有效调控子群内粒子数、粒子总数、子群数可以将ICPSO算法的理论优越性变为现实性。根据基本原理,局部最优及早熟可以通过分组避免,该方式通过将子群最优信息引入迭代方程并采取分组方式获得,因此,子群数的提高在一定范围内有利于改善收敛精度。但是,在此过程中,收敛速度也会由于额外信息的引入受到影响,也就是说,在某种程度上,ICPSO算法的收敛精度是以寻优速度为代价换取的。另外,当粒子总数给定,收敛精度也会因子群数产生负面影响。因为,当粒子总数确定,子群数增加,子群内的粒子数必然变小,导致该子群最优信息与其他子群最优信息之间的差别性不足,同时,对内代表性不足,无法充分体现算法初衷,考虑增加分组数对收敛速度的影响,算法的总体性能会有较明显下降。另外,当确定子群数,存在双向性的粒子总数变化影响,也就是说,总粒子数被适当增加,子群内粒子数即可提高,群间差别性及最优群内代表性会相应提高,其收敛精度也得以提高,同时,对收敛速度的影响并不大,当粒子数被进一步提高,导致群内粒子数过大,群数下降,群差别对全局最优修正力不足,而粒子数的增加导致收敛精度改进不足,这与收敛速度的问题又彼此制约,导致算法整体性能下降[11]。

2.2 ICPSO优化BP神经网络

利用ICPSO对BP神经网络的权值及阈值进行优化处理。首先,通过将BP网络结构中的各层权值和阈值映射为粒子的速度,建立BP网络结构与粒子群算法的联系通道,再利用神经网络结构算出其对应输出,同时,将网络实际输出与目标输出代入适应度函数,计算均方误差,以此作为后续粒子群寻优的基础,最后,利用粒子群合作式寻优过程获得全局最优位置,从而得到网络的最优权值和阈值,至此,该网络模型得以构建完成。

ICPSO优化的BP神经网络的具体实现过程如下。

第一步,构建三层BP神经网络,并对其进行初始化。

1)层数设计:网络层数设计为3层,即输入层、输出层、隐层层数。

2)输入层节点数设计:基于光纤SPR传感器的神经网络补偿原理,SPR传感器通过检测共振波长、半峰全宽以及共振点极值来反映被测环境介质的折射率,故输入节点数设计为1∼3个,用以建立不同结构的神经网络,以验证不同光谱信息(共振波长、半峰全宽以及共振点极值)表征测量的组合能力。

3)隐层节点数设计:利用经验近似公式来确定隐层节点数,算法可表示为

式中:n1为输入层节点数,n2为隐层节点数。

4)输出层节点数n3设计:基于SPR传感器神经网络补偿原理,补偿结构输出可以无限逼近被测介质折射率的输出,故设计网络输出节点为1个,表征为被测介质折射率。

5)适应度函数的设计:利用训练中产生的均方误差作为ICPSO的适应度函数,具体定义为

式中:l为训练样本数,n3为输出节点数,yk为BP网络训练实际输出,tk为目标输出,即被测介质折射率的真值。

第二步,对粒子群进行初始化。

1)加速系数c1,c2的设计:经仿真最后确定取c1=c2=2.05;2)惯性因子ω的设计:经仿真最后确定ω=0.9;3)粒子的数量设计:经仿真最后确定取粒子数N=160;4)代次数设计:根据实验中具体的寻优效果取k1=100;5)r1,r2设计:由经验数据,设计其取值为介于[0,1]之间的随机数;6)对于合作粒子群中的子群数r的设计:基于前期研究结论,子群数较多时,可参考的子群最优值信息多,粒子多样性好,全局寻优能力得到优化,但子群数过多,反而使得子群内粒子数少,子群最优信息的子群内代表性、子群间差异性不足,从而导致其寻优精度下降,甚至可出现精度劣化,训练过程将对子群数分别取2、4、6、8组,并取精度最高的一组输出作为网络的结构权值及阈值,子群数r初始化为2组;7)粒子维数设计:基于本节利用粒子群算法ICPOS对BP网络权值和阈值进行优化处理的目标,粒子维数d设计为

式中:p为输入层-隐含层连接权个数,n2为隐含层阈值个数,q为隐含层-输出层连接权个数,n3为输出层阈值个数。

第三步,利用适应度函数计算全局最优值pg、个体最优值pi以及子群最优值pr。

在设计中,先将各粒子的位置及速度初始化为随机数,同时,将各个粒子分成2组,并将各个粒子不同维数所代表的连接权或阈值代入BP神经网络的结构参数计算公式中,分别计算网络隐层节点及输出层节点的输出,通过适应度函数计算网络实际输出与目标输出的均方误差,最后,经比较获得初始化pg、pi及pr。

第四步,根据合作粒子群更新公式(3),调整各粒子的速度vt+1及位置xt+1。

第五步,更新最优值。

根据适应度函数来比较当前最优值与pg、pi及pr三者的关系,若当前最优值优于其中任何一个参数,即将其替换。

第六步,检查结束条件。

如果叠带次数k大于给定最大次数k1或评价用误差值大于给定值,则整个程序停止迭代,并转第七步,否则,程序转到新一轮的粒子位置及适应度计算的过程(即第四步)。

第七步,保存该组全局最优值。

第八步,检查分组结束条件。

如果分组数为8组,则转第九步,否则分组数加2,并将粒子按规定分组,转第四步。

第九步,根据适应度函数比较各个分组输出全局最优粒子的位置,并将其中位置最优的一组全局最优粒子位置映射为神经网络的权值及阈值。

3 优化结果

3.1 实验数据采集

在测试过程中,首先采集待测试水质样品,并将其分类为预测集样品及训练集样本。其中训练样本集经过两方面处理,一是经由阿贝折射率仪进行真值测定,并作为ICPSO-BP神经网络的输出,一是经SPR开环传感系统测试而获取其光谱信息,并通过后续光谱处理算法提取其三个信息,分别为共振波长、半峰全宽及共振点极值,作为神经网络的输入,由输入输出数据构成的训练样品集对网络进行训练,当训练结束网络收敛后,该传感测量校正模型即创建成功;另一方面,预测样品集也同样经过以上2个处理步骤,该组样品集的真值和光谱信息用作模型校验,通过将其对应的共振波长、半峰全宽以及共振点极值信息输入已建立的ICPSO-BP模型中,获得网络对应输出,再将其与真值进行比较,从而验证网络的可行性。

在测试过程中需要确定折射率的样品集,采用甘油配置不同浓度溶液,再利用阿贝折射仪测试其折射率作为预测和训练样本的目标值,具体实验系统为反射式SPR检测系统,如图3所示。其中,SPR传感器纤芯选用石英光纤,并利用离子束溅射法在其端面镀银膜(50 nm)。白光光源产生的入射光(波长为400∼1000 nm)通过P偏振片后再由Y型光纤耦合器的一端进入,经其另一端传入传感光纤,并作用于SPR传感头,该入射光线与液体介质相互作用会产生SPR效应,最后由端面全反射镜形成反射光线,通过Y型光纤出射端送光谱仪,利用计算机处理获得被测介质的待测信息。

图3 光纤SPR传感器检测实验平台Fig.3 Experimental platform of optical fiber SPRsensor

将光纤SPR传感器放入配置好的甘油溶液中,利用光谱分析仪采样其输入光谱,并利用光谱分析软件采集至电脑,获取所有溶液的光谱信号,求取滤波后光谱线的归一化强度为0.5处对应的波长间距,即半峰全宽(FWHM),同时采集滤波后光谱曲线的共振波长及共振光强,整理待训练数据,如表1所示。

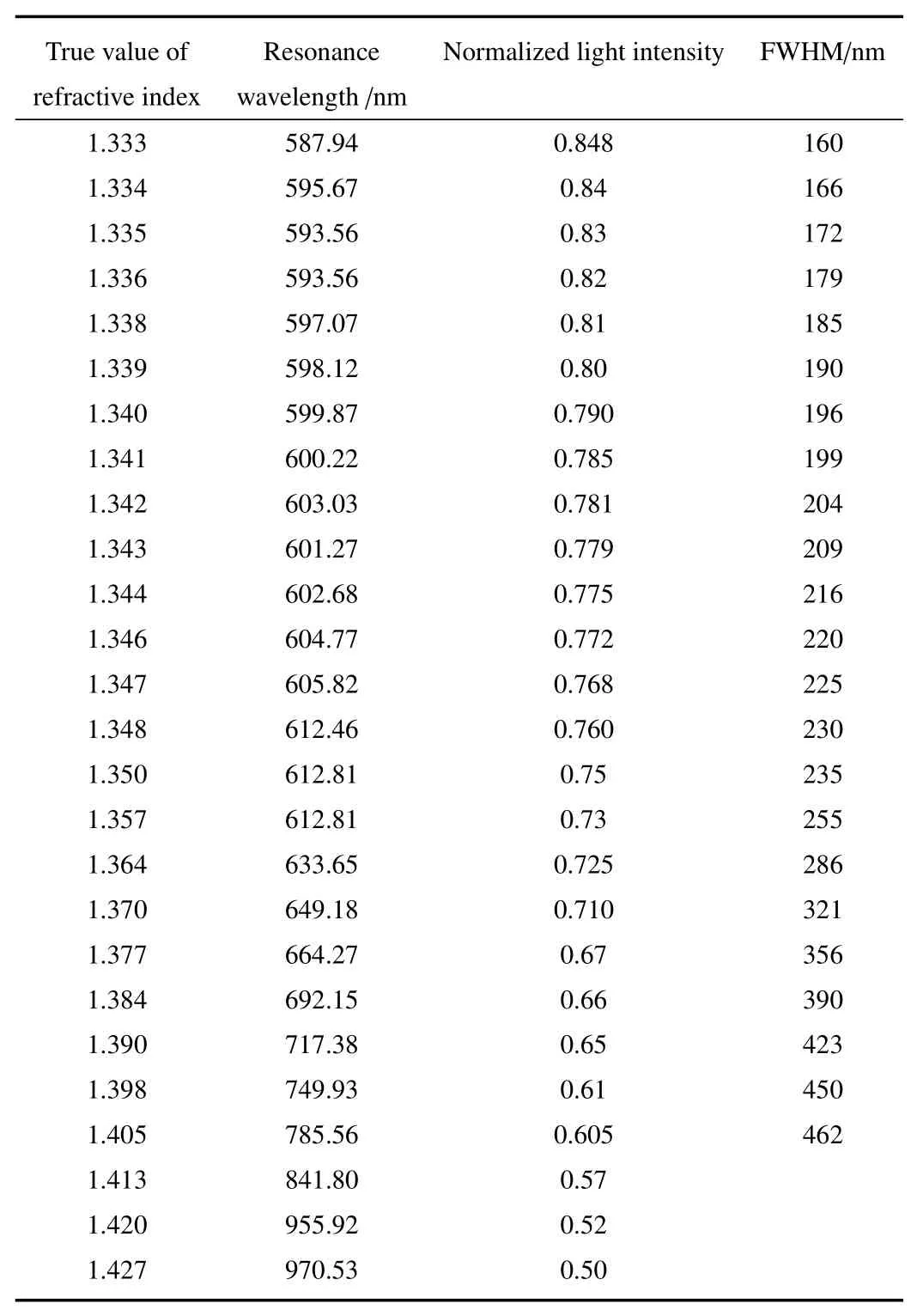
表1 不同折射率待测液体参数Table 1 Parameters of liquid to be measured with different refractive index

可见,当被测介质折射率在1.333∼1.427范围内变化时,光谱均呈现共振点,且共振波长随折射率增大而增大,并在587.94∼970.53之间变化,归一化共振强度则呈下降趋势,在0.809∼0.606之间变化,FWHM随折射率增大而增大,在160∼462之间变化。但是,归一化共振光强、波长、半峰全宽与折射率的关系均呈一定程度非线性关系,这就是传感系统固有的测试结构带来的本质问题。

在训练之前,共振光强可以由光谱仪直接获取其归一化数据,而其他参数的样本数据差别较大,若直接进行训练,则会导致延长网络训练时间,甚至可能影响整个网络无法收敛,故对样本进行归一化处理,以保证将不同量纲和取值的样本数据变换为相同取值尺度范围[−1,+1]内。第i个样本数据的归一化值可表示为

式中:xi为第i个样本数据实际值,xmax为该样本集最大值,xmin为该样本集最小值。

3.2 仿真实验

基于归一化共振光强、波长、半峰全宽与折射率的关系均呈现一定程度非线性,针对这种光纤SPR开环传感系统的固有结构问题,提出如图1所示的模型对其进行补偿。通过SPR传感器输出的光谱信息u可以获得三个与其输入折射率相关的参数:共振波长、共振光强、半峰全宽,为了获得更为良好的补偿效果,利用三个参数分别建立单输入、双输入、三输入类型的神经网络,并将表1中的归一化数据作为样本,其中,实验样本中的奇数序号数据用于训练,偶数序号数据用于预测,通过MATLAB 6.5编写补偿模型的仿真程序,完成如下验证实验。

1)建立单输入ICPSO-BP神经网络的非线性补偿模型

建立单输入ICPSO-BP神经网络的非线性补偿模型,以共振波长、共振光强、半峰全宽分别作为输入,对应实际被测折射率作为输出,训练ICPSO-BP神经网络。ICPSO-BP的主要参数设置如下:适应度函数为均方误差,网络训练算法为改进ICPSO,加速系数c1=c2=2.05,惯性因子ω=0.9,粒子数N=160,初始迭代次数k1=100,r1、r2为介于[0,1]之间的随机数,子群数r分别取2、4、6、8,r初始化为2,输入神经元个数为1,隐层神经元个数为3,输出神经元个数为1。

基于三个参数所建立的非线性补偿模型分别如图4∼6所示。

图4 共振波长非线性补偿模型Fig.4 Nonlinear compensation model of resonancewavelength

模型建立并训练成功后,将表1中的偶数序列数据作为预测数据,输入以上训练好的网络中进行检验,获得如图7所示的校正结果。

图5 共振光强非线性补偿模型Fig.5 Nonlinear compensation model of resonance intensity

由图7可见:三种不同输入下的校正效果差别较大。其中,以共振波长作为输入所建立的ICPSO-BP补偿网络的校正效果最好,其次是以共振光强作为输入的情况,最差为以半峰全宽作为输入的情况,计算可知三种情况下的最大绝对误差分别为0.005、0.006、0.008,也就是说,在等离子共振传感器的测试参数中,利用共振波长信息表征被测信号的特征性更强,但无论单独利用以上任何参数作为输入,都难以再达到与理想特性更为接近的线性关系,其表征效果有待完善。

图6 FWHM非线性补偿模型Fig.6 Nonlinear compensation model of FWHM

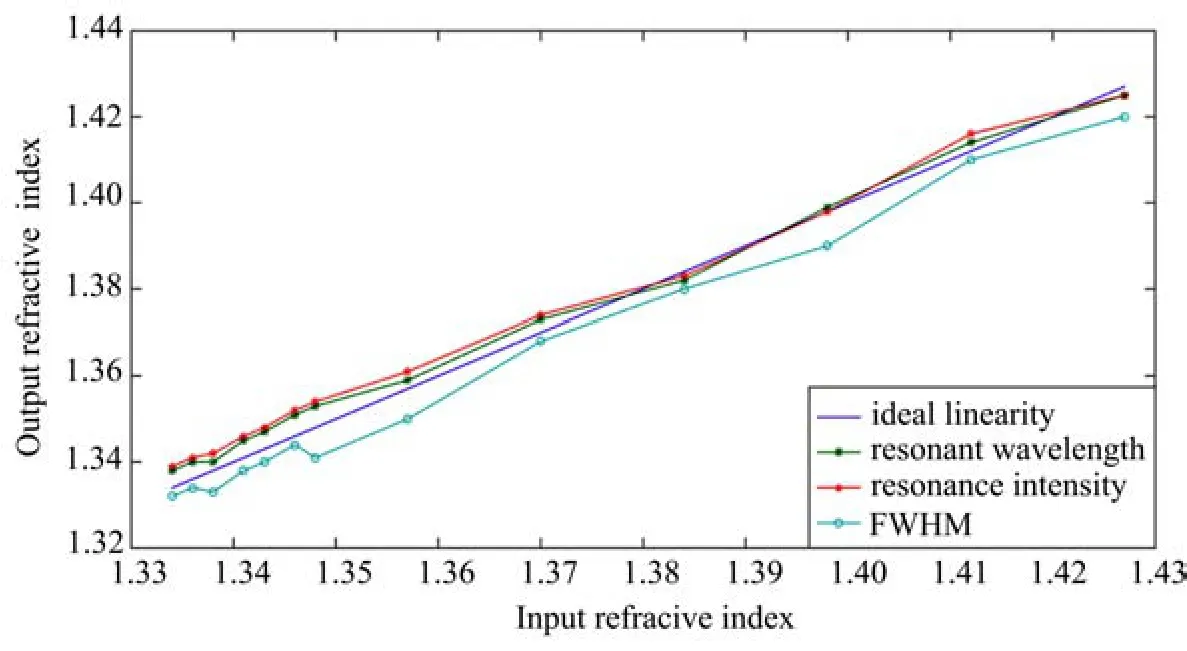
图7 单输入ICPSO-BP补偿后传感器的输入输出关系Fig.7 Relationship between input and output of sensor by single-input ICPSO-BPcompensation

2)建立双输入ICPSO-BP神经网络的非线性补偿模型

建立双输入ICPSO-BP神经网络的非线性补偿模型,并以共振波长与光强、共振光强与半峰全宽、共振波长与半峰全宽作为其两个输入信号,以实际被测折射率作为输出对网络进行训练。ICPSO-BP参数设置为:输入神经元个数为2,隐层神经元个数为5,输出神经元个数为1,其他结构参数同上。

以上三种情况的实验结果如图8所示。由图8可见:三种情况下的非线性校正能力比较接近,但相对来说,从校正误差来看,以共振波长与光强作为输入的组合校正效果最好,其次是以共振光强与半峰全宽作为输入的情况,最差是以共振波长与半峰全宽作为输入的情况,计算可得三种情况下的最大绝对误差分别为0.003、0.004、0.005,从稳定性方面来看,前两种情况的初期波动都较大,后期较为稳定,而最后一种情况的共振波长与半峰全宽作为输入的组合,其校正效果最为稳定,但缺点是误差相对偏大。总体来说,与单输入形式相比,各种双输入的校正效果都有了一定程度的改善,这也说明:在校正过程中,模型同样需要尽可能全面的参考信息,信息越全面越具有代表性,从而在不深入了解传感器内部结构的情况下,很好地解决SPR传感器的“黑箱问题”,保证补偿系统线性关系体现得更为良好。

图8 双输入ICPSO-BP补偿后传感器输入输出关系Fig.8 Relationship between input and output of sensor by dual-input ICPSO-BPcompensation

3)建立三输入ICPSO-BP神经网络的非线性补偿模型

建立三输入ICPSO-BP神经网络的非线性补偿模型,以共振波长、共振光强与半峰全宽作为其三个输入信号,以实际输出折射率作为输出对网络进行训练。ICPSO-BP参数设置为:输入神经元个数为3,隐层神经元个数为7,输出神经元个数为1,其他结构参数同上。

将三输入与双输入、单输入校正获得的最好非线性校正结果进行比较,获得如图9所示的结果。其中,单输入、双输入与三输入的最大绝对误差分别为0.005、0.003、5×10−4。与双输入和单输入校正最好的情况相比较,三输入ICPSO-BP的预测结果与理想线性非常接近,其主要原因是三输入ICPSO-BP网络结构可以更为全面地借鉴传感器输入输出关系的参考信息,使其具有更为良好的非线性映射和逼近能力,从而更好地消除SPR结构对传感性能的影响,保证其校正的线性化程度更为优良。

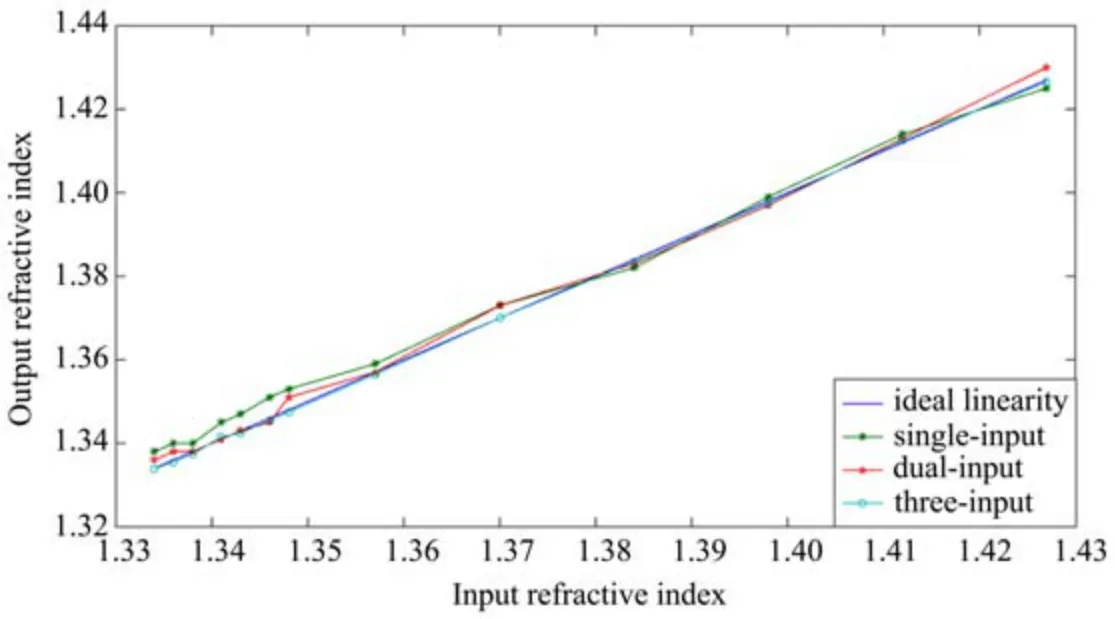
图9 三输入ICPSO-BP补偿后传感器输入输出关系Fig.9 Relationship between input and output of sensor by three-input ICPSO-BPcompensation

另外,抽取部分实验数据进行泛化能力检验,测试结果如表2所示。根据表2测试数据并结合具体真实值可知:各组测试误差均小于0.001,也就是说,利用三输入ICPSO测试被测介质折射率,具有很强的泛化能力,从而进一步证实了三输入的ICPSO-BP神经网络在等离子共振传感器非线性校正中的可行性。

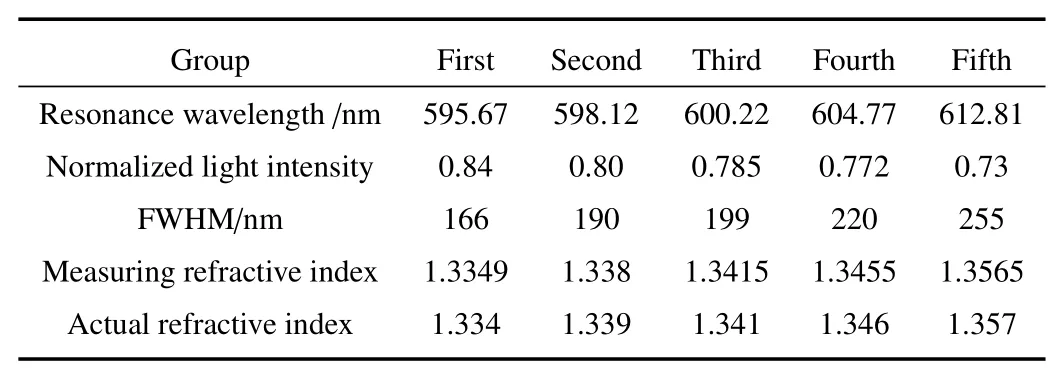
表2 ICPSO-BP神经网络泛化能力检验Table 2 Test of generalization ability of ICPSO-BPneural network

4)建立三输入不同神经网络非线性补偿模型

为了验证神经网络在光纤SPR传感器非线性校正中的作用以及ICPSO-BP神经网络算法的可行性,利用MATLAB编程,分别建立RBF、BP、PSO-BP以及ICPSO-BP神经网络对SPR传感器进行非线性校正,各种网络均设置为三输入,其他主要参数如下。

传统BP神经网络训练采用误差反向传播学习算法,网络层数为3,输入层神经元个数为3,隐含层神经元个数为7,输出神经元个数为1,初始权值取为[−1,1]之间的随机数,学习速率为0.1,期望误差为0.001,隐层神经元采用Sigmoid函数,具体定义为

PSO-BP和ICPSO-BP网络权值寻优的最大进化代数为100,适应度函数为均方误差,加速系数c1=c2=2.05,惯性因子ω=0.9,粒子数N=160,初始迭代次数k1=100,r1、r2为介于[0,1]之间的随机数,输入神经元个数为3,隐层神经元个数为7,输出神经元个数为1,其他网络结构方面的参数设置同传统BP网。另,ICPSO-BP涉及到的子群数r取2、4、6、8组,r初始化为2组。RBF网络的均方差精度为0.02,散布常数为1,输入及输出神经元个数等同BP网络,隐层神经元数在网络工作时通过自适应来获得,其他参数等同BP网络设置。四种网络的校正结果如图10所示。

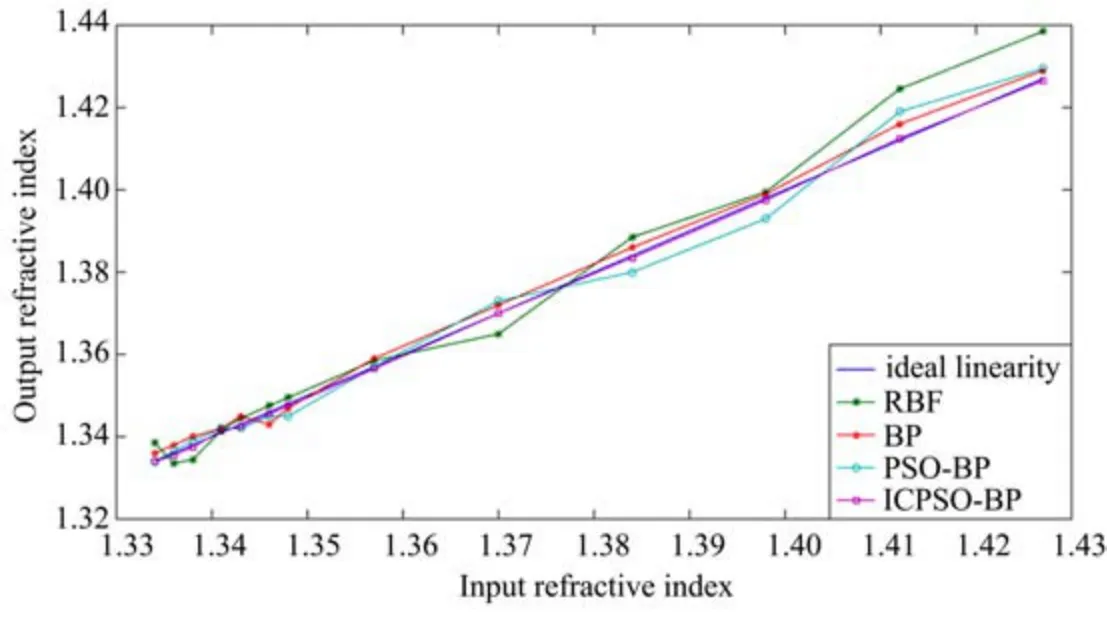
图10 不同神经网络校正比较Fig.10 Comparison of different neural network

由图10数据计算得到RBF、BP、PSO-BP、ICPSO-BP四种网络的最大绝对误差分别为0.013、0.004、0.007、0.001,统计其误差标准差分别为0.005、0.002、0.003、0.001。由此可见,RBF网络校正效果最差,BP网络校正效果较好,PSO-BP网络校正效果不稳定,前期效果较好,后期则线性程度退化,主要原因是PSO本身寻优过分依赖全局最优信息导致易陷入局部最优,这与粒子早熟收敛有关,从而影响寻优及校正效果;而ICPSO-BP在整个输入范围内都表现良好,根本原因是引入子群最优信息,且通过迭代次数动态调整子群最优信息与全局最优信息的作用,寻优前期以全局最优信息引导为主,随着寻优过程的深入,子群最优信息作用逐渐提高,从而保持粒子多样性,使得该神经网络泛化能力更强,保证ICPSO-BP补偿模型与等离子共振传感器所组成系统具有更为良好的线性及更高的测试精度。

进一步获得四种神经网络测量结果,见表3,并获得四种神经网络的校正误差曲线及训练误差曲线,如图11、12所示。

表3 各神经网络补偿模型测量结果对照Table 3 Comparison of measurement resultsof each neural network compensation model

由图11可知,在1.334∼1.427折射率测量范围内,RBF、BP、PSO-BP、ICPSO-BP算法的最大测量误差分别为0.013、0.004、0.007、0.001,也就是说,ICPSO-BP算法的校正误差最小,具有最高的精度,从而进一步验证了该算法在光纤SPR传感器非线性校正中的可行性。另外,由图12可见,在设置训练目标精度为0.001的情况下,BP神经网络只需要8步就可以达到预定目标,ICPSO-BP和PSO-BP网络则分别需要13和16步,速度最慢的为RBF网络,需要21步,与RBF、BP、PSO-BP相比,ICPSO-BP算法的校正精度最高,且其学习训练速度也与其他网络速度相当,也就是说,在通过分组提高算法精度的前提下,其速度也可以得到保证。

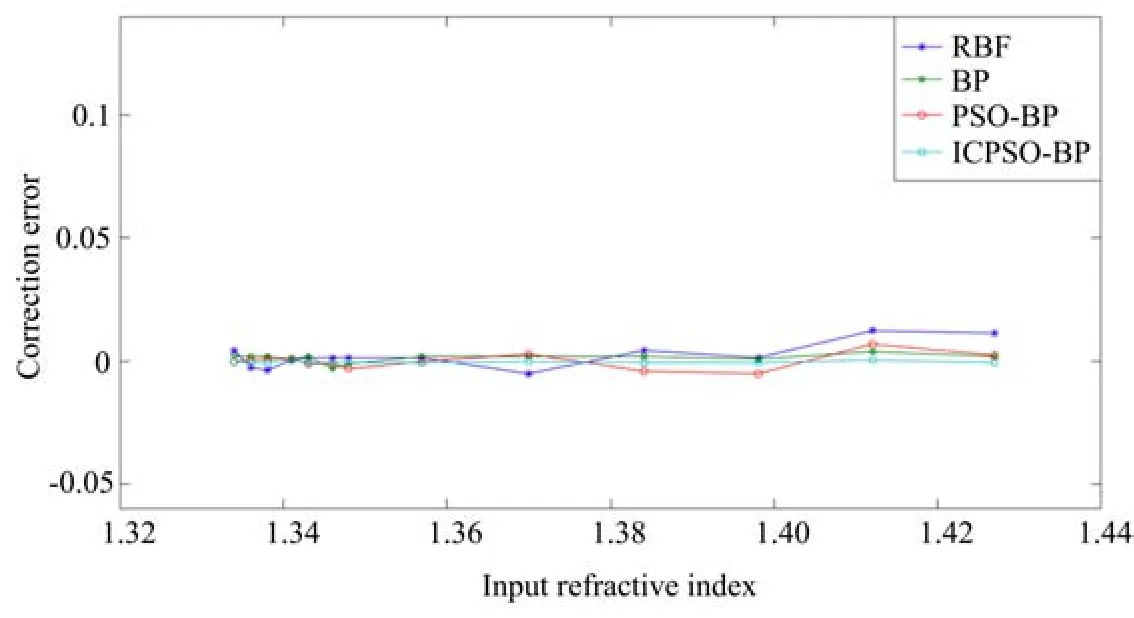
图11 各神经网络校正误差Fig.11 Correction error of each neural network

图12 各个神经网络训练误差曲线Fig.12 Training error curveof each neural network

4 结论

针对光纤SPR开环系统的弊端,利用ICPSO-BP神经网络对光纤SPR测试系统模型进行辨识补偿,基于人工神经网络的开环结构进行分析、讨论与实验研究,建立光纤SPR补偿模型,通过SPR传感器输出的光谱信息获得三个与其输入折射率相关的参数:共振波长、共振光强、半峰全宽,并利用三个参数分别建立单输入、双输入、三输入三类神经网络,将归一化测试数据作为训练和预测用样本数据,利用MATLAB 6.5编写仿真程序,验证了该补偿模型在光纤SPR测量精度和速度上的可行性,从而为光纤SPR传感器的进一步应用打下一定的基础。在人工神经网络设计方面,基于神经网络训练问题属于非线性高度复杂优化问题,而梯度下降训练方法依赖初始权重选择,算法复杂且易陷入局部最优,研究全局搜索算法PSO,并针对其可能出现早熟收敛的问题进行改进,提出一种动态信息调整且速度可控的改进型合作粒子群算法ICPSO,将其作为神经网络的训练算法,通过在粒子飞行状态控制的迭代方程中引入子群最优信息,利用寻优次数对全局最优信息、子群最优信息进行融合与动态调控,较好地保持了粒子多样性,从而有效地避免粒子的早熟收敛,实现较好的寻优精度。