基于粗糙集理论的多标记数据互补决策约简加速算法

李 华,王思宇,王雅茹

(石家庄铁道大学 数理系,河北 石家庄 050043)

0 引 言

现实世界中，一个样本可能同时与多个标记相关联，被称为多标记学习。例如，一幅图片可以同时具有沙滩、山和天空等多个信息标注[1]；一首音乐可以表达开心、高兴和放松等多种情感类[2]。由于多标记学习框架更加准确地刻画了实际应用中大量存在的多义性现象[3]，因而被广泛应用于文本分类[4]、图像标注[5]和社交网络[6]等领域。

随着信息技术的高速发展，视频、文档和音频序列等多标记数据的维数显著增加，呈现出高维化的趋势。多标记数据的高维特征不仅增加了计算成本和存储代价，而且还会导致所谓的“维数灾难”[7]问题，因此对多标记数据的高维特征进行降维处理显得尤为重要。

众多的降维技术中，基于粗糙集理论[8]的特征选择方法受到了广泛关注。在粗糙集理论中，特征选择也称为属性约简，其是在保持可识别能力不变的情况下，通过去除冗余特征来获取知识的属性约简。近年来，已有学者将粗糙集理论的属性约简技术应用于多标记学习。段洁等人应用前向贪心策略提出了基于邻域粗糙集的多标记特征选择算法[9]；H.Li等人提出了基于粗糙集理论的互补决策约简启发式算法，去除不必要属性的同时保持了由标记所传递的不确定性不变[10]；Y.Lin等人提出了多标记模糊粗糙集理论并给出了相应的属性约简方法[11]；Y.Li等人提出了一种基于模糊粗糙集的多标记特征选择算法[12]；Z.Qiao等人利用标记集正域进行多标记数据的属性约简[13]；W.Qian等人基于特征依赖度和粗糙集理论，提出了标记分布学习的特征选择算法[14]。

上述针对于多标记数据的属性约简算法都能有效地减少冗余属性，但对于大规模数据集而言，他们都不同程度地存在着计算耗时较大的问题。因此，多标记数据属性约简算法的加速机制就成为了一个亟待解决的关键问题。

在粗糙集理论中，基于集合的包含关系，当属性幂集中的属性集由粗到细变化时，可以确定由粗到细的粒度序列，称为正粒化序列[15]。当粒度由粗到细变化时，目标概念的正域逐渐增大。如果逐步去掉正域，那么数据集的规模会逐渐缩小。本文首先研究了当数据集规模逐步缩小时，互补决策约简中属性外部重要度的保序性质。特别地，当粒度由粗到细变化时，在逐步去掉正域的数据集上，具有最大外部重要度的属性是保持不变的。基于此，本文提出互补决策约简启发式算法的一种加速算法，该加速算法是在粒度由粗到细的变化过程中，通过逐步去掉正域来降低数据集的规模，缩短计算约简的时间；同时，虽然数据集的规模不断缩小，但具有最大外部重要度的属性是保持不变的，而约简是通过不断在核属性集上增加具有最大外部重要度的属性得到的，因此加速算法可以得到与原算法相同的互补决策约简。

1 基本概念

1.1 多标记决策表

多标记数据可以用多标记决策表[10]S=(U,A,L)来形式化表示，其中U={x1,x2,…,xn}是对象集合，称为论域；A={a1,a2,…,am}是条件属性集合，称为条件属性集；L={l1,l2,…,lq}是标记的集合，称为标记集。每个条件属性a∈A形成一个满射a:U→Va，其中Va表示条件属性a的值域。每个标记l∈L形成一个满射l:U→Vl，其中Vl={0,1}表示标记l的值域。如果对象x和标记l相关联，那么l(x)=1，否则l(x)=0。

在多标记决策表中，条件属性集A与标记集L互不相交，即A∩L=∅；U中的每一个对象至少关联于标记集L中的一个标记[16]；L中的每一个标记至少与U中的一个对象相关联[17]。本文不考虑无标记的对象。

下面是多标记决策表的一个实例。

例1多标记决策表S=(U,A,L)是由中医冠心病数据集[18]中部分数据组成，如表1所示。论域U={x1,x2,x3,x4,x5}为患者集合。条件属性集A={a,b,c}是由3个症状组成的条件属性集，其中条件属性a表示“胸痛特点”，其值域为{1 隐痛 2 刺痛 3 胀痛}；条件属性b表示“诱发因素”，其值域为{1 劳累后加重 2 饮酒后加重 3 气候骤冷加重}；条件属性c表示“心悸”，其值域为{1 出现 2 不出现}。L={l1,l2,l3}是由3个证型组成的标记集，其中l1表示“心气虚”，l2表示“心阳虚”，l3表示“气滞”。显然，U中的每个对象至少关联于L中一个标记，L中的每个标记至少关联于U中的一个对象。

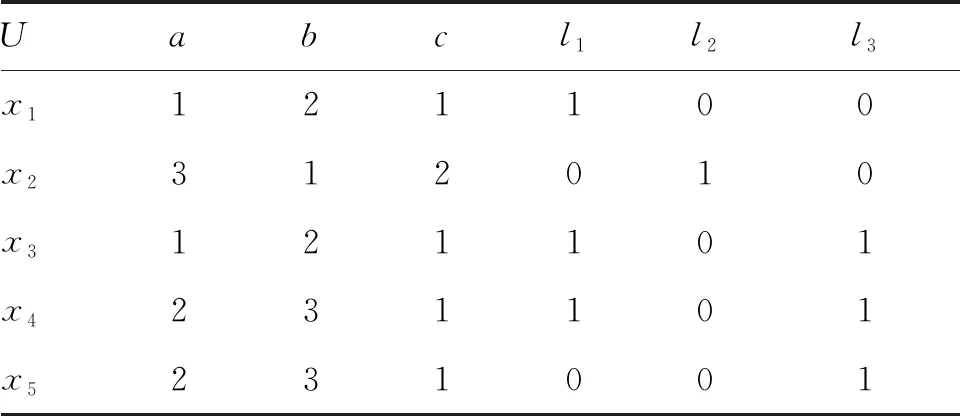
表1 多标记决策表S=(U,A,L)

1.2 互补决策约简

定义1[10]设S=(U,A,L)是多标记决策表，其中A={a1,a2,…,am}，L={l1,l2,…,lq}。给定一个标记li∈L，称

Ei={x∈U:li(x)=1}

(1)

为对应于标记li的一个标记信息集。

标记信息集是所有与标记li相关联的对象集合，描述了多标记数据中隐含的标记信息。

(2)

(3)

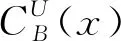
定义3[10]设S=(U,A,L)是多标记决策表，B⊆A。B称为S的一个互补决策约简当且仅当B满足下面的条件：

(1)对任意x∈U，

(4)

(2)对任意的B′⊂B，存在x∈U，使得

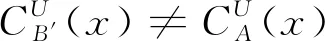
(5)

若B只满足条件(1)，则称B是一个互补决策协调集，否则称B是不协调的。

2 动态粒度下多标记决策表的粗糙集近似

由等价关系所确定的分划为描述目标概念提供一个粒化世界[19]。用一组具有偏序关系的等价关系族来刻画目标概念被称为动态粒度下的粗糙集近似[15]。如果在这种粒度变化下，采用逐渐细化的思想，即粒度由粗变细，称为正向近似。对于粒度计算和粗糙集理论，动态粒度下的正向近似思想为其提供了一个新的研究方向，并且在属性约简算法中得到了广泛且有效的应用[20-21]。本节主要探讨动态粒度下多标记决策表的粗糙集近似及其相关性质。

设S=(U,A,L)是多标记决策表，在2A上定义偏序关系≤：设P≤Q(或者Q≥P)表示P比Q精细(或者Q比P粗糙)，当且仅当满足对任意的Pi∈U/P，存在Qj∈U/Q使得Pi⊆Qj，其中U/P={P1,P2,…,Ps}和U/Q={Q1,Q2,…,Qt}分别是由P,Q⊆A所确定的划分。如果P≤Q且U/P≠U/Q，称P严格细于Q(或者Q严格粗于P)，用PP)来表示。

性质1[10]设S=(U,A,L)是多标记决策表，设B,C⊆A，那么

(1)如果B≥C，则

(6)

(2)对任意x∈U，

(7)

下面由粗决策函数和细决策函数来定义多标记决策表的正域。

定义4设S=(U,A,L)是多标记决策表，B⊆A，对于任意x∈U，标记集L关于条件属性集B的正域定义为：

(8)

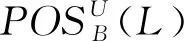
下面基于动态粒度下的正向近似思想表示正域。

定义5设S=(U,A,L)是多标记决策表，B={R1,R2,…,Rn}是属性集族，其中R1≥R2≥…≥Rn(Ri∈2A)，设Bi={R1,R2,…,Ri}，标记集L关于Bi的正域可表示为：

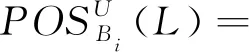
(9)

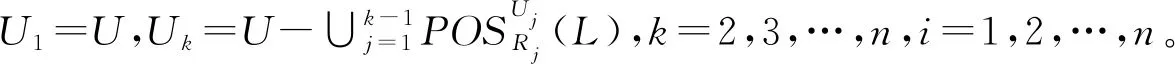
性质2设S=(U,A,L)是多标记决策表，B={R1,R2,…,Rn}是属性集族，其中R1≥R2≥…≥Rn(Ri∈2A)，设Bi={R1,R2,…,Ri}，则

(10)

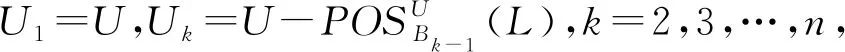
i=1,2,…,n。

证明：根据定义5，可得

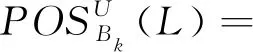
其中，U1=U，

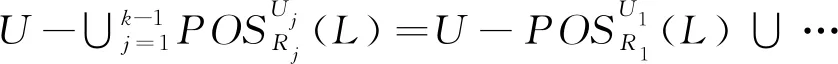
性质2表明标记集L关于属性集族Bk的正域可由属性集族Bk-1的正域和在逐渐减少的论域上的属性集Rk的正域来表示。

性质3设S=(U,A,L)是多标记决策表，B={R1,R2,…,Rn}是属性集族，其中R1≥R2≥…≥Rn(Ri∈2A)，设Bi={R1,R2,…,Ri}，i=1,2,…,n，则

(11)

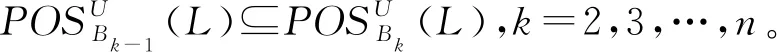
性质3表明随着属性集族中属性集数目的增加，标记集L关于属性集族的正域是单调递增的。

3 多标记数据互补决策约简加速算法

当粒度由粗到细变化时，在逐步去掉正域的多标记决策表上，互补决策约简中属性外部重要度具有保序性质，并基于此提出互补决策约简启发式算法的加速算法。

3.1 属性重要性的度量

定义6[10]设S=(U,A,L)是多标记决策表，B⊆A，条件属性集B的标记依赖度为

(12)

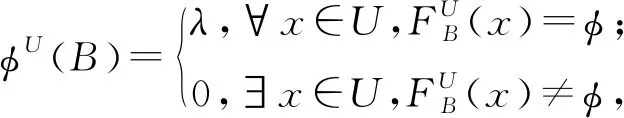
这里λ∈(0,1)是常数。

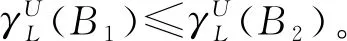
标记依赖度反映了条件属性子集B对标记集L的近似能力或依赖程度，由依赖度也可以定义每个条件属性的重要度。

定义7[10]设S=(U,A,L)是多标记决策表，B⊆A，a∈B的内部重要度定义为：

(13)

定义8[10]设S=(U,A,L)是多标记决策表，B⊆A，a∈A-B关于B的外部重要度定义为：

(14)

不同的条件属性在保持标记不确定性方面的作用是不同的，可将这些属性分为两类：不必要的和必要的。

定义9[10]设S=(U,A,L)是多标记决策表，B⊆A，称条件属性a∈B是B中的不必要属性，如果对于任意的x∈U，

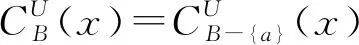
(15)

否则称a为B的必要属性。

A中所有必要属性组成的集合称为A的核，记为CORE(A)。

下面性质表明核可由内部重要度定义。

性质5[10]设S=(U,A,L)是多标记决策表，则

CORE(A)={a∈A:Siginner(a,A,L,U)>0}

(16)

标记依赖度和属性的内部重要度也可用于描述互补决策约简。

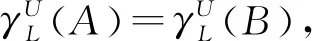
由性质5可知，通过计算属性的内部重要度可得到多标记决策表的核属性集。然后，依次在核属性集上添加具有最大外部重要度的属性，可以得到一个互补决策协调集。由定理1，若该互补决策协调集中的每个属性都是必要的，则该互补决策协调集为一个约简。基于上述理论，文献[10]提出了互补决策约简启发式算法，用来计算多标记决策表的一个互补决策约简。

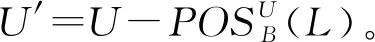
定理2表明在多标记决策表中，在原始数据集和去掉正域的数据集上，属性基于外部重要度的序是保持不变的。因此，在约简的启发式算法中，在去掉正域的数据集上具有最大外部重要度的属性也是原始数据集上具有最大外部重要度的属性。所以，该定理保证了去掉正域的数据集的约简和原始数据集的约简是相同的，其为互补决策约简的加速算法提供了理论保证。

3.2 互补决策约简的加速算法

互补决策约简的加速算法，其主要思想为：首先计算属性内部重要度来寻找多标记决策表的核属性集RED。在核属性集的基础上，逐次从数据集中去掉已选属性集对应的正域，然后在剩下的数据集上选择外部重要度最大的属性，依次放入属性集RED中，直到该特征子集满足停止准则，就得到了多标记决策表中的一个互补决策约简RED。

算法1互补决策约简的加速算法(A-CDR)。

输入：多标记决策表S=(U,A,L)；

输出：S的一个互补决策约简RED。

1.令RED=∅；

2.for (k=1;k≤|A|;k++)

{计算Siginner(ak,A,L,U)；

如果Siginner(ak,A,L,U)>0，

则RED=RED∪{ak}；}

3.令i=1，R1=RED，B1={R1}，U1=U；

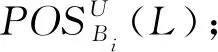
i=i+1；

依次计算并选取

Sigouter(a0,RED,L,Ui)=max{Sigouter(aj,RED,L,Ui),aj∈A-RED}

RED=RED∪{a0}；

Ri=Ri-1∪{a0}；

Bi={R1,R2,…,Ri}；}

5.输出属性约简结果RED。

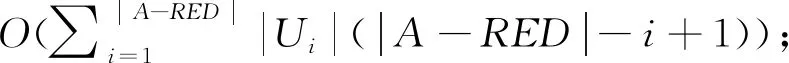
4 实验及分析

本节在6组多标记公开测试集上比较互补约简启发式算法(CDR)和加速算法(A-CDR)的计算性能。表2为数据集的详细信息。

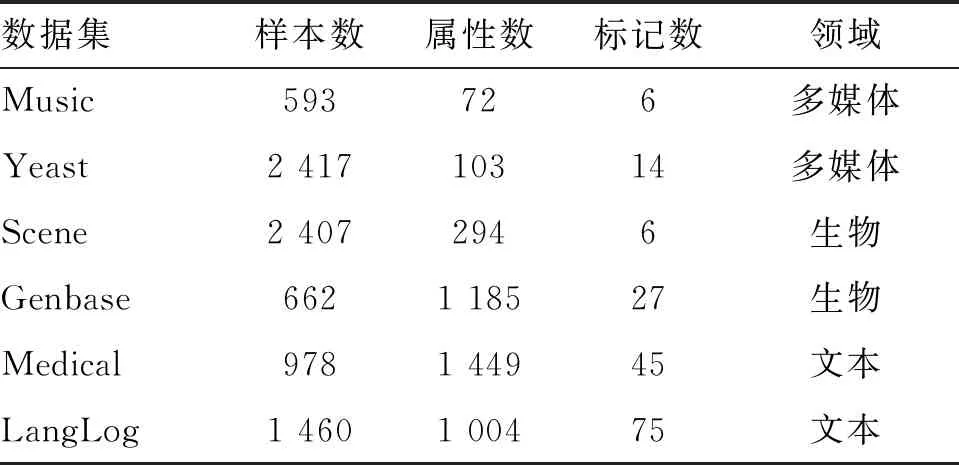
表2 数据集

本次实验在硬件配置为Intel(R) Core (TM) i5-5200U CPU @2.20 GHz，内存4 GB的计算机上，用Matlab语言编程实现算法。依赖函数中的参数λ设置为0.1。

表3列出了两种算法在6个数据集上属性约简的结果和计算时间。

由表3可知，在同一个数据集上，加速算法可以得到和原始算法相同的约简，但加速算法的计算时间明显减少。

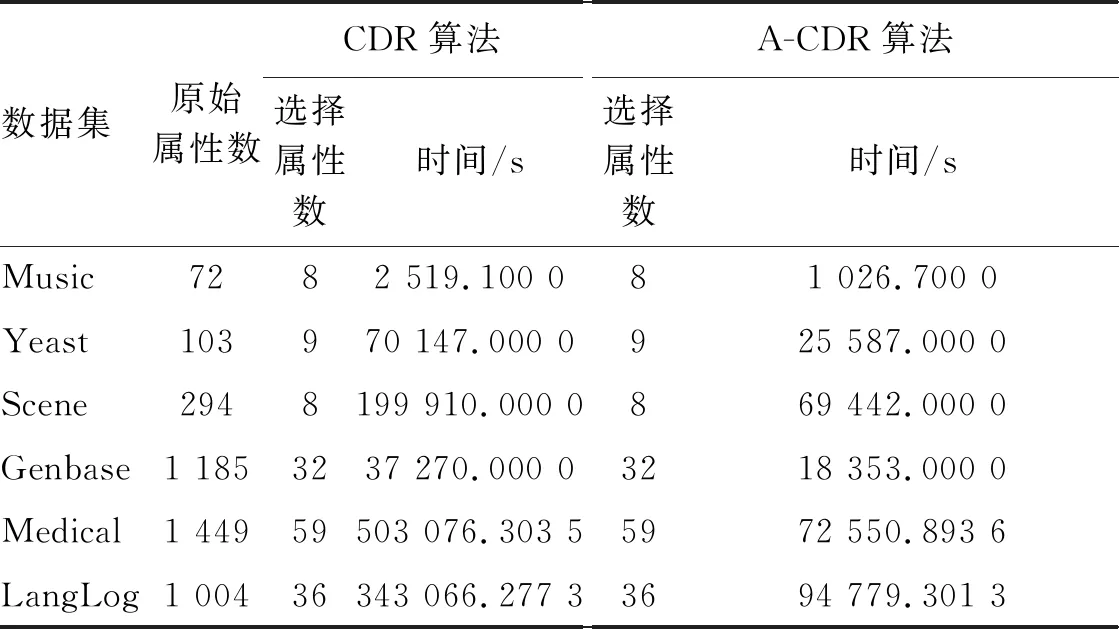
表3 CDR算法和A-CDR算法的约简结果及计算时间

为了更好地比较两种算法计算约简的时间，表2中的每个数据集都被平均分为20份，记为xi(i=1,2,…,20)，实验所使用的20份数据中的每一份记为Xi(i=1,2,…,20)，其中X1=x1，X2=x1∪x2，…，X20=x1∪x2…∪x20，最后一份数据即是数据集本身。

图1是两种算法分别在6组数据集上的约简计算时间，其中X轴表示上述20份样本数目由少到多的数据集Xi(i=1,2,…,20)，Y轴表示算法在不同数据集上的计算时间(单位：秒)。

如图1中(a)～(f)实验结果所示，随着数据集规模的增加，原始算法和加速算法计算约简的时间也在增加。样本的数据规模越大，两种算法计算约简的时间消耗差值就越大。这表明加速算法有效地加速了属性约简的过程，对于大规模的数据集来说，加速算法的计算效率更高，更加高效。

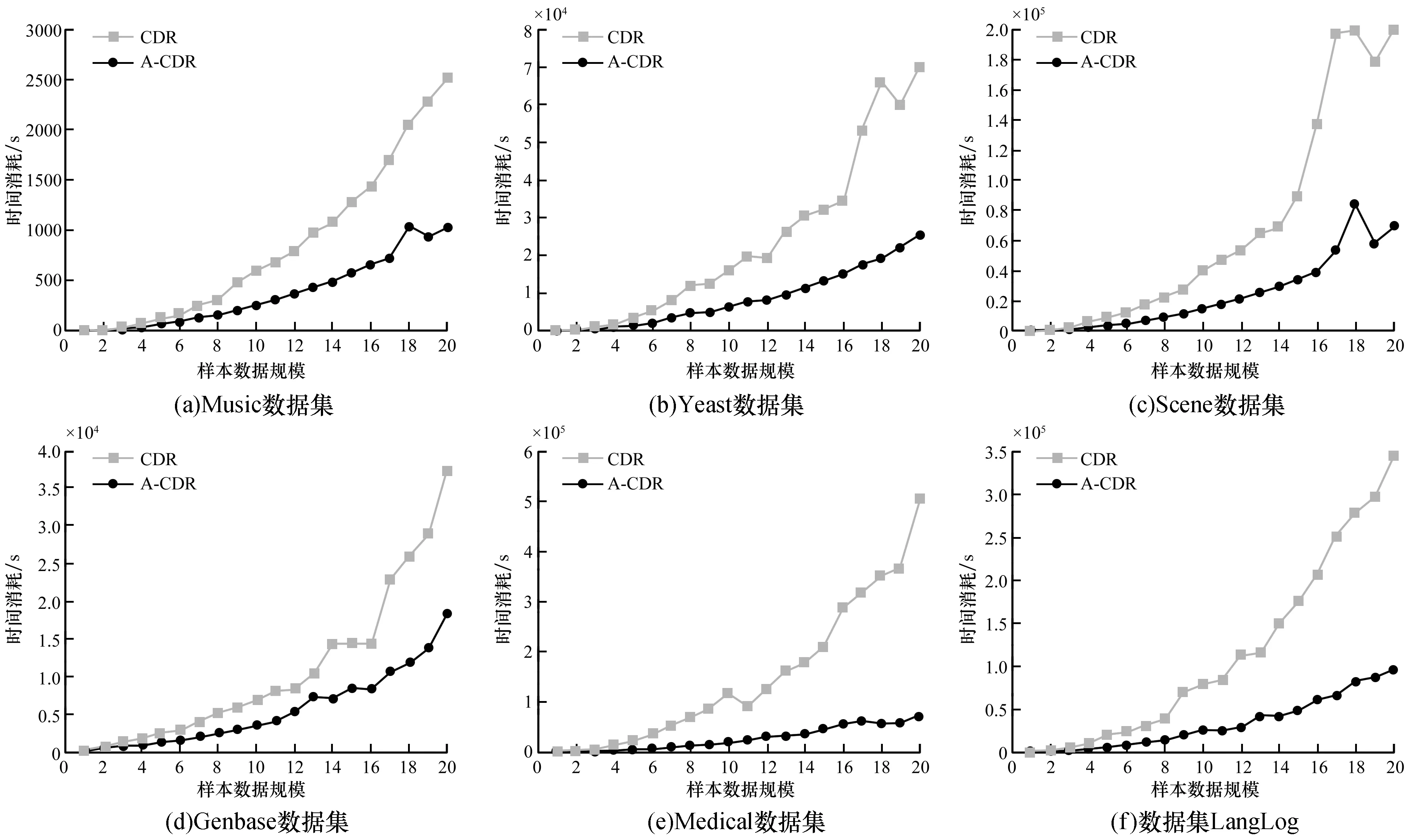
图1 CDR与A-CDR的计算时间

5 结 论

针对互补决策约简启发式算法计算耗时过大的缺陷，本文首先研究了动态粒度下互补决策约简的属性外部重要度的保序性质，并基于该性质，提出了互补决策约简启发式算法的加速算法。该加速算法通过逐步缩小数据规模来降低计算耗时，加速了属性约简的过程，并且可以得到与原始算法相同的约简。最后，在多标记数据集上有效地验证了加速算法的有效性。