沥青混合料复合结构层间稳定性破坏研究

彭 成,方 凯*,钟启明

(1.南华大学 土木工程学院,湖南 衡阳421001；2.南京水利科学研究院,江苏 南京 210000)

0 引 言

沥青路面结构由多层组成，S.Hakimzadeh等认为沥青路面上下层之间的层间稳定性是影响路面使用寿命的关键问题之一[1]。一方面，直接拉拔、剪切等试验是评价沥青路面层间稳定性的重要方法，而剪切试验存在着操作复杂所需试样较多，主应力方向固定不变，而且是在轴对称情况下进行的，与实际情况尚不能完全符合。另一方面，有限元模拟也是分析其层间稳定性的有效手段。

然而，实验只能观察路面结构的宏观破坏模式，并获得有限的参数或变化趋势。为了研究沥青混合料的低温强度，A.C.Falchetto采用了间接拉拔和半圆弯曲试验方法，获得沥青混合料的名义强度和断裂参数[2-3]。也有学者通过黏结强度试验，W.Huang和Q.Lv研究了影响沥青与集料黏结强度的因素[3]。此外，为了验证相关的层间实验和补充多尺度试验数据，相关学者基于内聚力模型建立了一系列二维有限元模型，基于内聚力模型方法估算了半圆弯曲试件沿裂缝表面的最大应力，结合间接拉拔试验，J.Gerber提出了基于半圆弯曲断裂试验的间接拉拔无缺口试件沥青混合料强度预测的新关系式。同时，有学者建立了基于内聚力模型的二维有限元模型，分析了各种破坏机理[4]，Y.Zhao通过简历模型，估算了沥青混凝土试件界面的抗裂性[5]。而采用双线性内聚力模型可以描述了黏聚力和位移，Y.R.Kim验证了双线性内聚力模型用于接触破坏的可行性[6]。

然而，二维模型很难量化沥青混凝土复合结构的层间破坏过程。因此，有必要进行三维有限元模拟，研究上下层界面的破坏。三维模型的收敛问题与计算精度之间存在矛盾，这是三维模型的模拟应该解决的问题。

沥青混凝土试验的加载速率一般小于60 mm/min[7]。采用隐式静力分析方法计算三维模型时，存在收敛问题。Dassault认为显式动力分析可以解决收敛问题，但计算精度较差，因此，综合考虑隐式静力分析与显式动力分析计算方法的优点和应用，准静态分析方法被应用于解决低速动力问题[8]。O.Kaitila采用这两种方法(准静态分析和隐式静态分析)，通过壳体有限元模型研究冷弯薄壁型钢箱形截面的腹板破坏行为，结果表明，隐式静态分析存在显著的收敛问题，而准静态分析可以解决收敛问题[9]，因此，准静态分析已经被越来越多的学者所认可。A.Baroutaji，Z.Fan等比较了管系在准静态动态横向载荷下的压碎行为和能量吸收响应，发现存在一个临界速度，该速度被确定为模态变化[10-11]。P.Natário采用壳体有限元模型和准静态分析方法分析了法兰破碎现象，讨论了不同参数对计算速度的影响[12]。因此，为了高效、准确地描述沥青混凝土的破坏过程，需要找到适合沥青混凝土的准静态参数。与此同时，Z.P.You利用X射线计算机断层成像技术建立了动态荷载作用下沥青混凝土的三维离散元模型，并采用频率温度监测技术缩短计算时间[13]。

针对上述问题，本文以拉拔破坏试验为例，基于双线性内聚力模型建立了相应的有限元模型，模型采用准静态法计算。同时，系统分析了影响模型计算效率和精度的参数，推荐了准静态计算参数。最后，根据推荐参数对模型进行了计算，从细观力学角度分析了沥青混凝土层间破坏过程。

1 直接拉拔试验

双层车辙板沥青混凝土试件(300 mm×300 mm×100 mm)，采用车轮碾压法成型。两层的沥青混凝土类型(AC-13)和沥青含量(按骨料重量计为4.7%)相同，在层间刷黏层油，黏层油用量为0.15 kg/m2。AC-13的骨料级配和黏结层的性能分别见表1和表2。

表1 AC-13试验用骨料级配

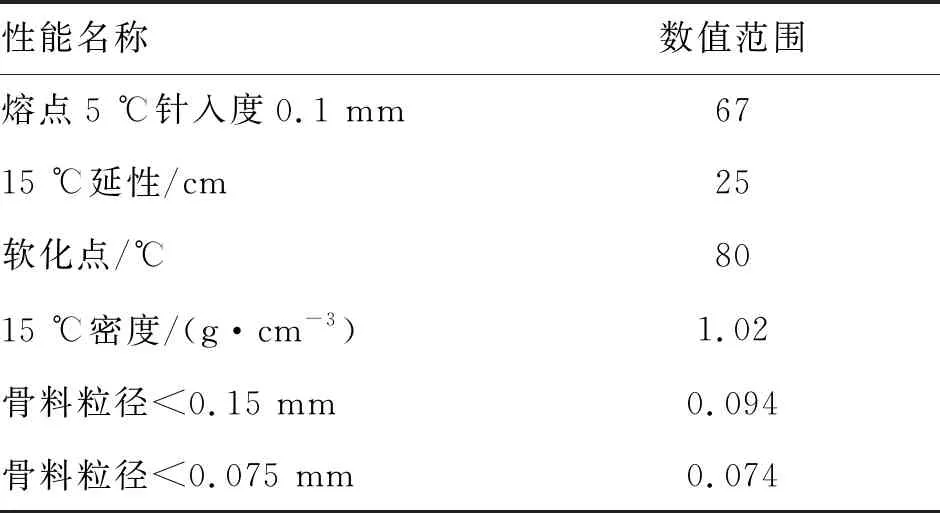
表2 黏结层(SBS聚合物改性沥青)材料的性能

从双层车辙板沥青混合料中钻取4个直径为100 mm的试件，如图1所示。试样干燥后，用高强度环氧树脂黏合剂将试样顶部和底部与金属拉延板黏合，黏合剂固化后，通过路面拉拔仪在20 ℃温度下进行拉拔试验，通过连接的计算机实时记录拉拔力随拉拔位移的变化趋势。当试样从沥青混凝土之间的界面断裂时，记录数据。实验拉拔速率分别为60 mm/min、30 mm/min和10 mm/min；每个拉拔速率条件的试验重复4次。

图1 拉拔试验过程

2 三维建模理论

2.1 内聚力本构模型

近年来，双线性内聚力模型被广泛应用于结构界面破坏分析。采用双线性内聚力模型可以模拟了沥青混凝土的断裂行为[14-15]。而以往的研究表明，双线性内聚力模型用描述于沥青混凝土的开裂过程[16-17]。

图2 典型双线性内聚力模型

双线性内聚力模型的本构关系可用式(1)表示：

(1)

初始刚度系数如式(2)所示：

(2)

标量损伤变量如式(3)所示：

(3)

在式(4)中，kn表示损伤起始和演化的程度。

(4)

表3 材料损伤模型参数

2.2 有限元模型

如图3(a)所示，模型与试验钻芯取样试件保持一致，直径为100 mm，高为100 mm，分为3层，即上、下面层与中间黏结层，上下用模具固定，计算时，以一定速率向Z轴方向移动，如图3(b)所示。在运动过程中连续读取张力，并根据读数计算黏结强度。

图3 拉拔系统有限元模型

应力与应变与随时间的变化，拟合公式为式(5)：

(5)

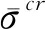
2.3 准静态分析方法

在动力学问题中运动方程为式(6)

(6)

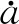
当进行准静态分析时，运动方程变为式(7)：

(7)

其中，K和Q(t)为刚度矩阵与荷载矩阵，质量矩阵可表示为式(8)：

(8)

其中，ρ表示密度，N表示差值函数，V表示体积，e为相关单元。

首先求解系统的自由振动方程，在式(8)中令Q(t)=0，即为式(9)：

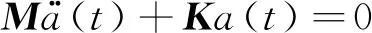
(9)

可以得到沥青最低阶模态频率为385.6 Hz。

3 准静态法的影响因素分析

任何计算和试验中都应考虑加载速率对沥青混凝土的影响。此外，在研究拉拔速率对计算效率和计算精度的影响之前，需要确定许多次要影响因素，如有限元网格尺寸、加载曲线和质量缩放。

3.1 网格尺寸和荷载曲线的影响

根据数值算例的计算结果，模拟拉拔速率取0.01 m/s。对于不同的单元长度，图4中比较了应力-位移曲线。很明显，由于曲线几乎重合，网格依赖性很小。考虑到精度和效率之间的平衡，在以下模拟中，所有网格中使用的单元长度为5 mm(网格1)。

图4 不同网格的平均应力-位移曲线

研究了三种加载曲线下的系统动态响应：抛物线(parabola，PA)、平滑线(smoothline，SM)和直线(straightline，ST)。荷载曲线如图5所示，其中t0为静态总荷载时间；t为加载时间；f(t)是荷载振幅。动能Ek和位移δ之间的关系用于评估荷载曲线，如图6所示。

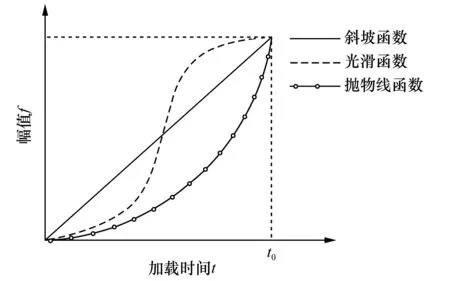
图5 三种不同的加载曲线

图6 动能Ek随位移δ的变化趋势

当加载曲线为PA时，Ek在很短的时间内直接从零增加到峰值。在后一阶段，它接近一个恒定值，即峰值的一半。以SM曲线加载时，动能Ek与位移关系为抛物线关系。当加载曲线为ST时，动能Ek呈现稳定的上升趋势，并在最后阶段达到峰值。

由以上分析可知，当加载曲线为SM时，Ek随位移δ关系与实际拉拔中的关系一致。因此，SM最有利于准静态拉拔系统稳定性。

3.2 质量缩放的影响

动态分析中，一次数值迭代对应一个关于幅值函数位移或荷载时间增量，表示为式(10)、式(11)：

Δt=Le/cd

(10)

(11)

式中：Le特征单元长度，cd材料的膨胀波速。E弹性模量，ρ材料密度。

由于采用质量缩放可以减少模型的计算时间，所以接下来拉拔速率取0.01 m/s，更接近试验的速率。在不同的质量缩放条件下，支反力R与位移δ的关系，动能Ek、内能Ei以及两者的比值Ek/Ei与位移的关系见图7。

图7 不同质量缩放条件下各评价指标随位移的变化趋势

如图7(a)所示，质量缩放不同时，支反力与位移的关系保持一致，差别不大，但质量缩放对黏结性的破坏较大，随着质量缩放倍数的增大，黏结性破坏程度越大。

能量方面分析，首先由图7(b)中Ek/Ei-δ可知，质量缩放系数越大，Ek/Ei的比值越大。以拉拔全过程Ek/Ei的比值大于5%的比例作为评价指标，具体见表4。由图7(c)可知，质量缩放对系统整体的内能没有影响。为了更清晰地分析质量缩放对动能Ek的影响，以lgEk为纵坐标绘制图7(d)。由图7(d)可知，质量缩放并不会影响动能的变化趋势，但是会引起动能以10倍数量级的增长。

表4 质量缩放的评价指标

3.3 加载速率的影响

一个准静态加载过程结束时其速度为零，此时分析即达到稳态。所以可加快分析过程中加载速率，只要结果保持与静态结果几近相同，而且动态效果保持不明显，就是可以接受的。质量缩放参数设定为100，拉拔速率设定为0.001、0.01、0.02、0.04、0.06、0.08和0.1 m/s。

当质量缩放取100，在不同的拉拔速率下的支反力R与位移δ的关系，动能Ek、内能Ei以及两者的比值Ek/Ei与位移的关系见图8。

图8 不同拉拔速率条件下各评价指标随位移的变化趋势

由图8(a)可知，当质量缩放取100时，拉拔速率对支反力随位移的变化趋势的影响较明显。拉拔速率从0.04 m/s增加到0.1 m/s的这个速率区间较明显，当拉拔速率小于0.04 m/s时，拉拔速率对支反力随位移的变化趋势的影响不明显。

所以，以黏结强度为评价指标，黏结强度按式(12)进行计算，可以得到如图9所示的黏结强度随拉拔速率的变化趋势图。

图9 黏结强度随拉拔速率的变化趋势

g=F/S

(12)

式中：g为黏结强度，MPa；F为破坏峰值，N；S为截面面积，mm2。

当模拟拉拔速率为0 m/s时，相应的黏结强度为0.041 7 MPa；当模拟拉拔速率为0.01 m/s时，相应的黏结强度为0.042 5 MPa。与0 m/s情况相比，黏结强度的相对差异为2%，因此当模拟拉拔速率采用0.01 m/s时，拉拔速率对黏结强度的影响可以忽略。

由图8(b)可知拉拔速率越大，Ek/Ei的比值越大，相应地(Ek/Ei<5%)的比值越小。以拉拔全过程Ek/Ei的比值大于5%的比例作为评价指标，具体见表5。

由图8(c)可知，拉拔速率对系统整体的内能没有影响。为了更清楚地研究模拟拉拔速率对Ek的影响，图8(d)使用了两个坐标系(lgEk和Ek)，对应于纵坐标Ek的模拟拉拔速率为0.02、0.04、0.06和0.08 m/s，对应于纵坐标lgEk的模拟拉拔速率为0.001、0.01和0.1 m/s。质量缩放并不会影响动能的变化趋势，但是会引起动能的量变，评价指标动能的最大值具体数值见表5。

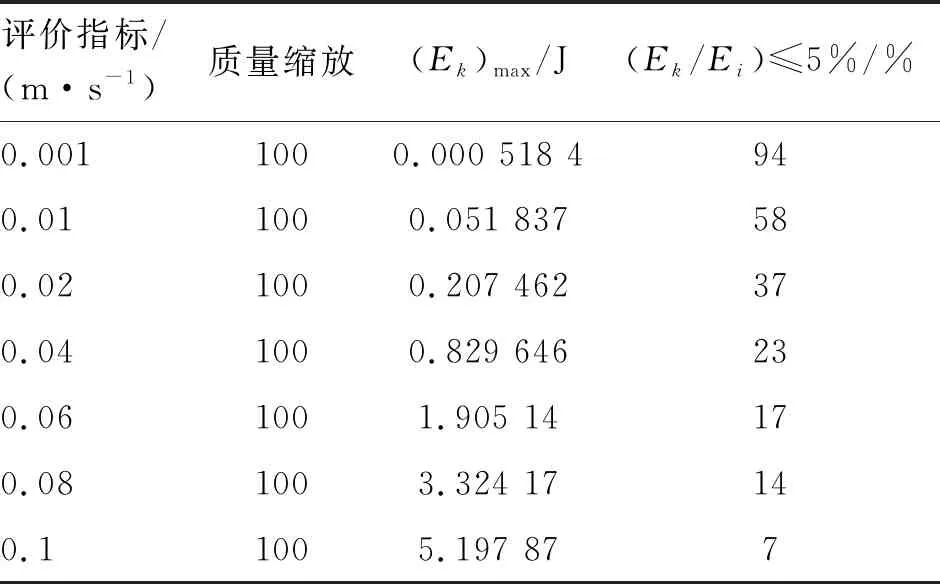
表5 拉拔速率评价指标

对(Ek/Ei<5%)的比例随拉拔速率的变化趋势进行非线性回归，可得式(13)

P(EK/Ei<5%)=86.107 97×(2.019 79×

10-26)v+11.896 02R2=0.982

(13)

当v≤0.014 m/s，P(EK/Ei<5%)值大于50%。由评价标准可知，此时的系统可以被当做准静态系统，所以为了取整，拉拔速率可取0.01 m/s进行模拟计算。

4 试验验证

综上所述，拉拔速率设计设计参数取0.01 m/s，质量缩放设计参数为100时，以平滑曲线形式进行加载，模拟结果可以与拉拔速率为0.001 m/s(60 mm/min)的拉拔试验相比较。有限元模拟(finite element simulation，FE)和试验(experiment，EX)的对比如图10所示。试验中拉拔试验速率设计参数为60、30和10 mm/min。当质量缩放为100时，模拟的拉拔速率是试验的10倍。

如图10所示，有限元计算结果与试验结果变化趋势一致，随着位移的增大，支反力呈现先增大后减小的趋势，这是因为当拉拔位移达到一定值时，上层与下层已经完全分离，层间已经完全被破坏，通过有限元结果与试验结果对比，说明准静态加载计算方式具有可靠性。

图10 有限元结果和试验结果的对比

5 层间破坏的细观力学响应分析

5.1 层间界面的应力分布

有限元模拟(拉拔速率600 mm/min)能较好地反映和模拟(拉拔速率60 mm/min)的力学响应。因此，可通过模拟来研究层间破坏力学响应(拉拔速率为600 mm/min)，不同位移下沥青混凝土上下层层间界面法向应力如图11所示。

图11 层间界面法向应力变化云图

如图11所示，拉拔时层间存在着应力集中现象，且最大应力集中位置分布存在着一定规律，即分布在图中标记的环形区域，因此，环形区域更容易发生破坏。

5.2 拉拔破坏过程的三个阶段

如图11所示，随着拉拔位移的增加，层间界面的应力分布存在应力集中现象。本文将正应力云图中最大正应力与平均正应力之比作为应力集中系数α。

应力集中区是法向应力云图中的环形区域，如图11所示。利用图像识别方法，将同一颜色区域内像素的累积，得到应力集中面积的数值。为了统一标准，将位移δ=2 mm的应力集中区域的面积设置为分母，其他位移下的应力集中面积为分子，在这种情况下，他们的比率是应力集中区域的比率。

在不同拉拔速率下，应力集中面积比与位移δ之间的关系如图12所示。

如图12所示，应力集中面积占比随着拉拔位移的增加，呈现明显的下降趋势。应力集中面积占比下降可以分为三个阶段：首先为膨胀阶段，此时应力集中面积占比呈现明显的线性减小趋势，下降速率较快；其次，为应力集中阶段，应力集中面积占比保持不变；最后，随着拉拔位移的增加，进入了损伤阶段，结构开始破坏，应力集中面积占比可以明确地反映其拉拔破坏过程变化。

如图13所示，层间最大应力随着位移的增加，呈现先增加、后降低趋势，其对应的破坏过程可以分为初始阶段、裂纹产生和扩展阶段以及破坏阶段。在初始阶段，随着位移的增加，层间应力开始出现，且慢慢变大；在裂缝产生阶段，当位移增大到一定值时，层间开始产生破坏，裂纹产生；在扩展阶段，位移迅速增大，层间应力也增加到其最大值，应力集中值达到最大；在破坏阶段，试件破坏已接近破坏尾声，随着位移的增加，试件最终完全破坏，应力集中现象消散。在拉拔破坏过程中，拉拔速率对层间最大应力的影响很小。如图12和图13所示,前两个阶段之间的区别在图12中更清楚。第二阶段的起点对应于试件的初始损伤，应予以重视。

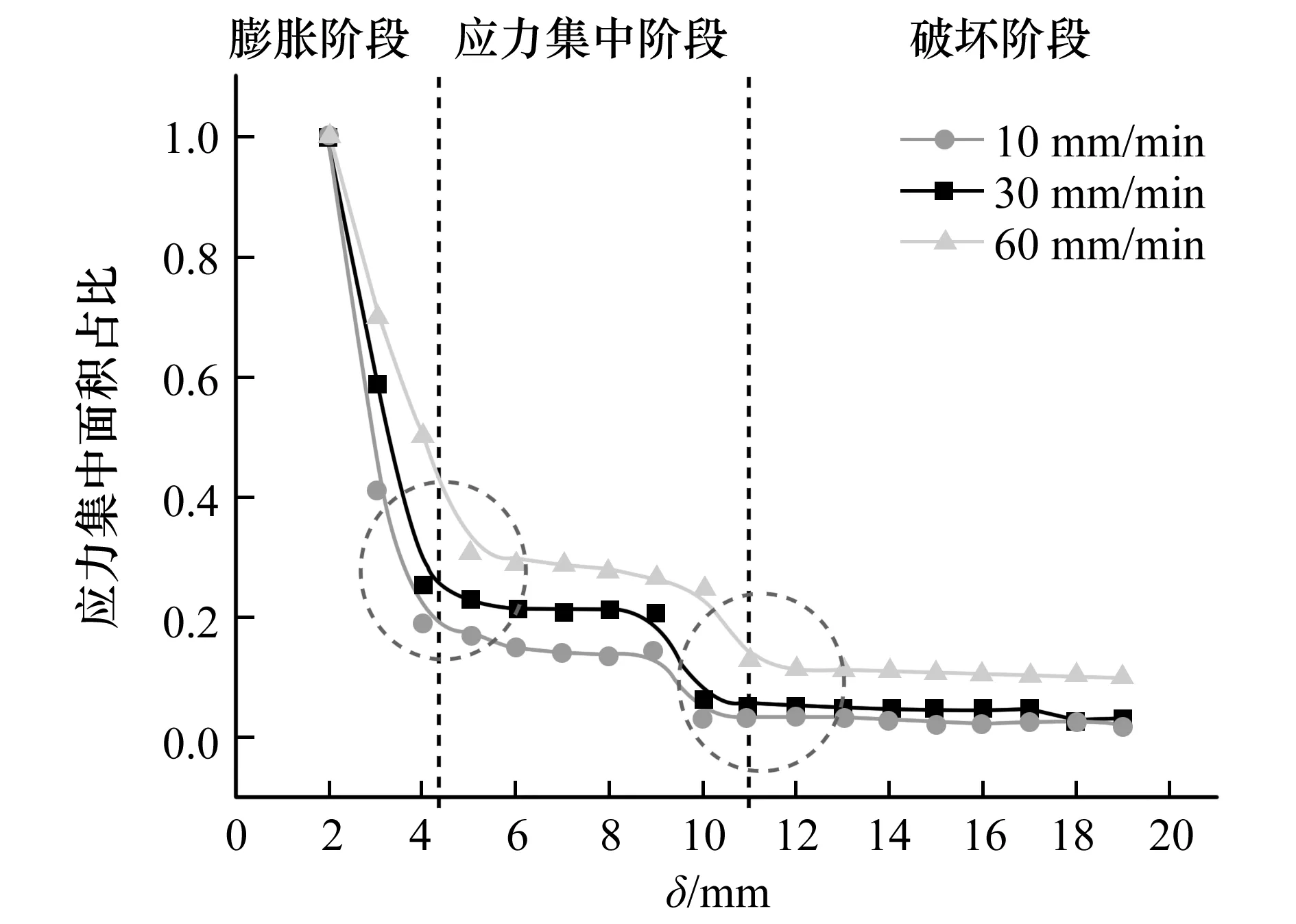
图12 应力集中面积比与位移δ的关系

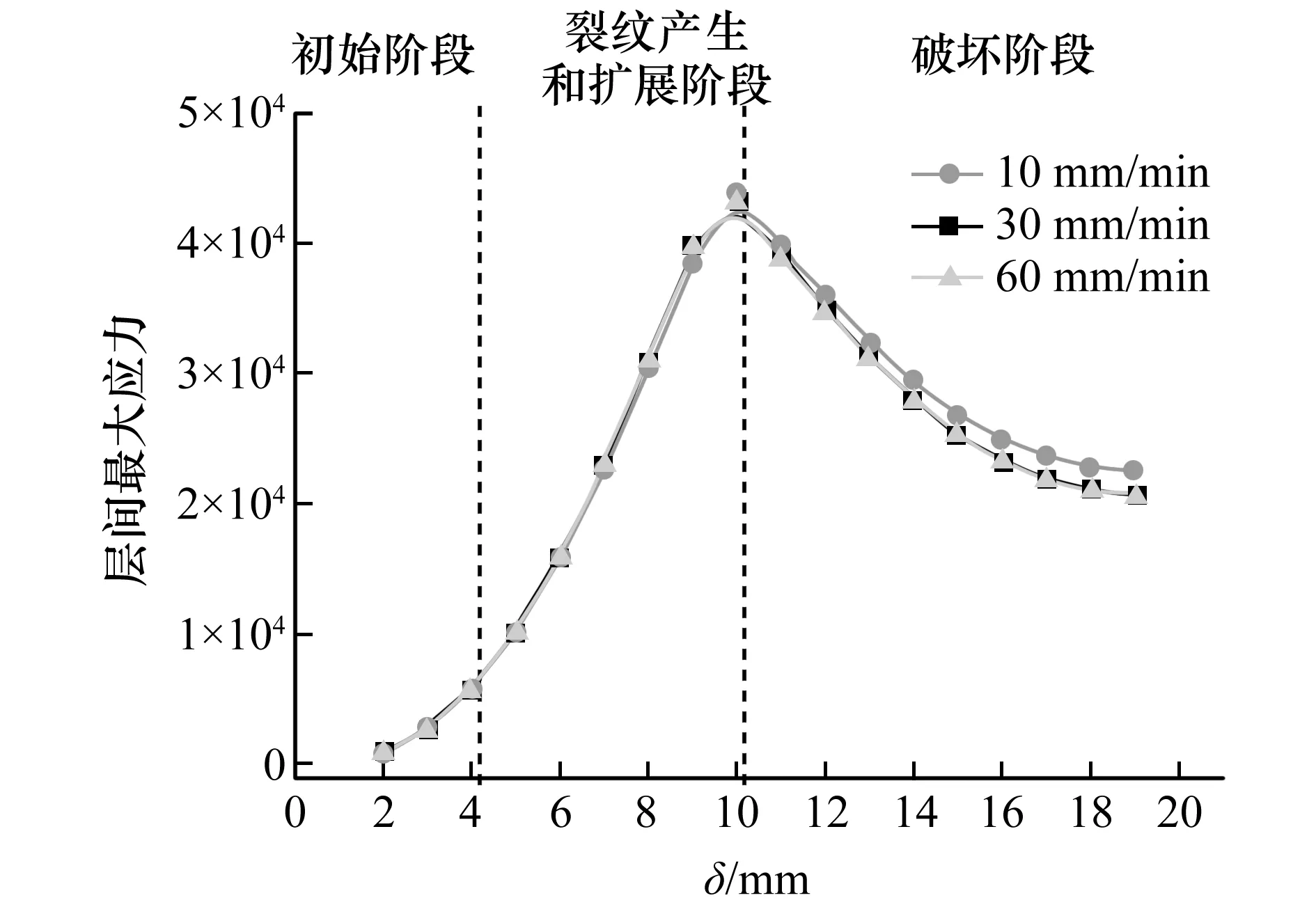
图13 层间最大应力与位移δ的关系

5.3 层间稳定性评价指标

拉拔速率是最重要的影响因素(如图15所示)，为了获得不同拉拔速率下的初始损伤位移，建立了回归方程的前两个阶段，如式(14)～式(16)所示：

(14)

(15)

(16)

式中：S是应力集中面积占比，δ是拉拔位移。

拉拔位移δ和应力集中面积比S之间存在的关系，如式(17)所示：

(17)

其中a、b、c为相关系数，均与拉拔速率相关。

通过对公式(17)求导，得到最大坡度变化点，作为第一阶段的转折点，即初始损坏点。可以得到不同拉拔速率下的初始损伤点，初始损伤位移与实验拉拔速率之间的关系如图14所示。

图14 拉拔速率与初始损伤位移之间的关系

如图14所示，初始损伤位移随实验拉拔速率的增加而线性增加。初始损伤位移与实验拉拔速率之间的关系为：

δI=4.65+0.022 7×v

(18)

其中：δI是初始损伤位移，mm；v是实验的拉拔速率，mm/min。

结果表明，拉拔速率越大，初始破坏位移越大。拉拔速率和黏结强度之间的关系与此一致。因此，初始损伤位移也可以作为层间稳定性的评价指标。

6 结 论

本文为了定量描述沥青混合料复合结构的层间破坏过程，基于双线性内聚力模型，建立了直接拉拔试验中圆柱形沥青混凝土的三维有限元模型。该模型采用显式准静态方法求解收敛问题。同时，研究准静态参数的变化对计算精度与效率的影响，主要结论如下：

1)双线性内聚力模型模型可应用于三维模型，可以描述沥青混凝土复合结构的层间拉拔破坏，包括损伤规律和破坏过程，当加载曲线为光滑线(SM)、模拟拉拔速率为实验的10倍、质量缩放为100时，准静态计算方法不仅解决了收敛问题，而且兼顾了计算效率和精度，并通过宏观实验对微观分析方法进行了验证。

2)拉拔破坏过程中层间界面的最大应力集中在环形区域。根据法向应力集中区随拉拔位移的变化，拉拔破坏过程呈现出三个阶段，即膨胀阶段、应力集中阶段和破坏阶段。

3)提出了初始损伤位移来评价拉拔速率对双层沥青混合料层间稳定性的影响。