高中数学课堂应用问题导学模式的策略

万广生

（甘肃省庆阳市环县第四中学，甘肃 环县 745700）

一、联系生活，巧设问题

（一）教师巧设问题

巧设问题是问题导学的第一项活动，也是有效应用问题导学模式实施高中数学教学的基础。新课标提出了数学教学生活化的倡导，要求教师紧扣数学与生活的关系，从生活中挖掘数学资源，在课堂上创设生活活动，引导学生们迁移生活经验体验课堂活动，掌握数学内容，增强数学认知。此外，学生们是沿着“波浪式前进”这一过程进行学习的。简单地说，已有经验和知识储备是学生们学习新知的基础。生活经验是学生们已有经验的重要构成。对此，在应用问题导学模式实施高中数学教学的时候，教师可以联系学生生活经历巧妙设置数学问题，引导学生们迁移生活经验进行探究。

以《直线与平面垂直的判定》为例。在生活中随处可见直线与平面垂直的现象，为教师设计生活化的问题提供了便利。所以，教师围绕挖掘到的直线与平面垂直的生活现象，设计了如此问题：

问题一：旗杆和地面的关系、旗杆和地面上的影子的关系、大桥的桥柱和水面的关系之间有哪些异同之处？

问题二：建筑工人在建房子的过程中，会使用一条绳子绑着小铅锤确定墙面与地面是否垂直，为什么要这样做？

如此问题中涉及的生活现象是学生们尤为熟悉的。受到熟悉的生活现象的影响，学生们会产生浓厚探究兴趣。特别的是，不少学生主动迁移生活的经验进行思考，顺其自然地与新知内容互动，为深入地探究、理解新知内容做好了准备。

（二）学生巧设问题

学生是体验生活的主体。在体验生活的过程中，大部分学生在数学认知的作用下，与部分生活现象进行了互动，窥探到了其中蕴含的数学内容，初步地建构了数学认知。已有数学认知是学生们自主提问的依据。学生们提出的问题，正是教师有效实施课堂教学的关键。所以，在应用问题导学模式实施数学教学的时候，教师要尊重学生们的生活经历，从生活中挖掘数学场景，并将其展现给学生们，引导学生们体验场景，迁移生活经验，自主地提出问题。

以《集合的概念》为例。在实施课堂教学之前，教师先利用导学案为学生们呈现了如此生活场景：“某超市周一早上购买了一批新鲜的水果和蔬菜，有苹果、西瓜等。新上任的采购员看到这些水果和蔬菜很是头疼，不知道如何处理这些水果和蔬菜。你有什么办法帮助采购员吗？或你可以根据这一生活场景提出哪些问题呢？”在导学案内容的作用下，大部分学生自觉迁移生活经验，按照蔬菜、水果的方式对其进行分类。在分类的过程中，部分学生提出了如下问题：“如何用数学的语言描述这样的分类情况？如此分类活动中包含了哪些数学知识？什么是集合？集合是由哪些对象构成的？”在了解了学生们提出的问题后，教师联系教学需要进行整理，选取恰当的问题展示给学生们。

采用SPSS 4.0统计学软件对数据进行处理，计量资料以“±s”表示，采用t检验；计数资料以百分数（%）表示，采用x2检验。以P＜0.05为差异有统计学意义。

如此做法，不仅使学生们与生活中的数学内容进行了互动，便于产生数学探究积极性，还使学生们在课堂上对熟悉的生活内容产生兴趣，自主探究问题，推动课堂教学发展，有利于提高课堂教学质量。

二、精心预设，提出问题

正所谓，凡事预则立，不预则废。教师的教学准备活动对实施课堂教学活动起着重要作用。新课标要求教师把握教学时机，做好教学预设。教学预设是教师应用自身的教学经验对教学做出的一种主观判断。教师的主观判断虽然和课堂教学实际情况存在出入，但却可以在一定程度上做到心中有数，有利于在课堂上冷静地对学生们进行引导，尤其根据课堂生成情况提出其他问题，推动课堂教学发展。所以，在应用问题导学模式实施数学课堂教学的时候，教师要先精心预设，接着提出设计好的问题。

比如，在《直线与平面垂直的判定》教学之前，教师可以先对设计好的问题进行分析，判断学生是否可以迁移生活解决这些问题、在解决问题的时候可能会出现哪些新问题等。接着，教师要针对预设的内容，设想其他问题，以此对学生们进行进一步引导。在预设问题的时候，教师还可以设计微课、自主学习任务单，辅助学生们自主学习新知内容。受到数学学习能力的影响，大部分学生存在自学问题。自学问题正是教师预设问题的抓手。教师可以课前引导学生反馈自学问题，分析问题成因，据此有针对性地预设其他问题，引导学生们迁移自学经验地进行深入探究。

如此做法，不仅可以使教师锻炼教学能力，提升专业水平，还可以夯实教学基础，引导学生们逐步思考、解决问题，提高课堂学习效果。

三、鼓励质疑，点拨引导

质疑是学生们学习主体性的具体体现。思考是学生们有效学习的“法宝”。在缺乏思考的情况下，学生们是难以对所学内容建构深刻理解的。应用问题导学模式实施数学教学的目的之一是引导学生们有效思考。大部分高中生思考能力不强，在数学课堂上往往难以自主思考问题。教师在数学教学中起着引导作用，是学生们思考的引导者。质疑是学生们思考的结果，是学生们发展思考能力的重要途径。所以，在应用问题导学模式实施数学教学的时候，教师要发挥好自身的教学引导作用，借助适宜的方式引导学生们质疑，并立足具体质疑内容对学生进行点拨，由此推动学生们分析、解决问题，理解所学，顺其自然地形成思考能力和质疑品质。

以《圆的方程》为例。在实施课堂教学活动的过程中，教师利用课件向学生们展现了如此问题：求解经过点（5，2）（-3，2）（3，0）的圆的方向。大部分学生迁移课堂所学，将三点坐标带入圆的方程中，通过求解方程的方式得出a、b、r 的值。此时，教师可以先评价学生们得出的结果，接着进行引导：“能不能从平面几何的角度求解出圆心呢？”受到教师的引导，部分学生产生疑问，同时产生了继续探究的兴趣，自主地从平面几何的角度进行思考。然后，教师对于学生展现的思考结果有针对性地给予点拨。如此做法，不仅使学生们多角度地思考、解决了问题，还使学生们因此开放了思维，便于提高思维水平。立足学生们的课堂学习情况，教师可以继续展示其他问题，引导学生们灵活地应用不同方法进行解决，同样地根据学生们的问题解决情况进行点拨，实现预期的教学效果，提高教学质量。

由此可见，在数学课堂上有效地引导学生们质疑，不但可以引导学生们一步步地探究数学，深入地理解数学内容，还可以使学生切实地锻炼数学思维能力和问题解决能力，有利于提高数学学习效果。

四、深入分析，探究问题

探究问题的过程是学生们建构知识，形成科学观念，掌握有效方法的过程。探究问题是问题导学模式的重要构成，直接影响问题导学模式的应用效果。教师是课堂教学的引导者，要引导学生们发挥自主性地解决问题。但是，大部分学生受到学习能力和问题解决能力的影响，在解决数学问题的时候会遇到诸多问题，不利于有效地解决问题。合作学习是学生们集思广益的主要途径。在体验合作学习活动的过程中，学生们会碰撞思维，获得解决问题的思路和方法，从而增强探究问题的有效性，为有效地解决问题奠定基础。

以《二面角的概念》为例。在实施课堂教学的过程中，教师结合重难点内容向学生们提出问题：“观察课件内容，思考如何能找到这样的平面角？”在提出此问题后，教师鼓励学生们在小组中进行交流，合作完成实验。为了使学生们顺利地解决此问题，教师做出如此引导：“在一个二面角模型上找到∠AOB，将这个角的顶点放到棱a 上，此时角的两边都位于两个平面内。据此可以得出这样的规定：如果能做到这一点，我们就可以用这个角的大小表示二面角的大小？你们觉得这个规定合理吗？说出理由。”

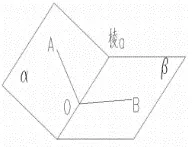
在教师的引导下，学生们继续合作探究。通过碰撞思维，大部分学生认为这样的规定是不合理的。因为改变∠AOB 的大小，如上规定是不变的。基于此，教师继续引导：“应用什么样的规定度量的方法才能使上述规定合理呢？”在教师的引导下，学生们继续探究。教学实践证明，教师的不断引导，不仅可以使学生们通过探究、解决一个个问题，逐步地掌握数学内容，还可以使学生们切实地锻炼数学探究能力、数学思维能力和合作学习能力，有利于提高数学学习效果。

五、应用探索，解决问题

解决问题是问题导学模式中不可缺少的一部分。这里的解决问题与上文提到的问题解决存在差异，主要是指学生们应用课堂所学解决问题。引导学生学以致用是新课标中提出的教学要求。学生们有效地学以致用，不仅可以加深对所学的理解，还可以锻炼应用能力。从上文论述可以看出，学生们在数学课堂上通过解决一系列问题，由浅入深地理解了数学知识。对此，教师要把握时机地设计练习题，引导学生们应用探索，灵活应用所学解决问题，提高知识学习效果。

以《等差数列前n 项和》为例。在学生们理解了等差数列前n 项和的公式之后，教师顺势呈现了如此练习题：已知等差数列的{an}的公差是2，第20 项a20=29，前20 项的和是多少？这个练习题难度不大，大部分学生迁移课堂所学可以解决。在学生们解决问题后，教师利用交互式电子白板随机选择学生展示解决问题的方法和过程，并有针对性地进行点拨。如此做法，不仅使学生们通过解决问题加深了对“知三求三”的理解，还因此实现了查漏补缺，有利于增强数学认知水平，提高课堂学习效果。

此外，教师还可以在课堂上引导学生们以小组为形式的合作设计练习题。因为设计练习题的过程是学生们应用所学的过程，合作设计练习题可以使练习内容愈加丰富，学生们通过大量练习可以加深对所学的理解。

六、走进生活，拓展问题

拓展课堂是新课标提出的一项要求，是学生们从数学课堂走向现实生活的主要途径。新课标指明了学生学习数学的目的是应用数学知识解决现实生活问题。拓展问题是拓展课堂的具体体现，是学生们带着数学问题走进现实生活中，在体验生活的过程中发现新问题、分析问题、解决问题的活动。结合生活拓展数学问题，不仅可以丰富数学问题内容，增强数学问题趣味，还可以使学生们通过解决问题加深对数学知识的理解，同时锻炼数学应用能力。此外，不少学生还因此意识到数学与生活有密切关系，便于用数学的眼光看世界，学会把数学知识应用在社会生活中，提高生活参与水平。

以《随机抽样》为例。在实施教学活动后，教师想到不少学生在课间讨论的《奔跑吧！兄弟》节目，决定针对高一、高二和高三开展一次抽样调查活动，了解学生们对该节目的看法。在开展抽象调查活动之前，教师立足高中三个年级学生的差异，以提高样本的代表性为目的，要求学生们在总体中选取10%的学生进行调查，确保样本容量与总体个数之间的比是1:10。之后，教师为学生们呈现调查内容：

1.你最喜欢《奔跑吧！兄弟》这档节目中的哪一项游戏？A.撕名牌；B.指压板；C.A 和B；D.其他。

2.你认为《奔跑吧！兄弟》这档节目有什么是值得学习的？A.这只是一档娱乐节目，娱乐众人罢了，没有什么可以学习的；B.兄弟们之间展现的合作精神是值得我们学习的；C.兄弟们在游戏过程中体现出的“友谊第一，比赛第二”的精神是值得我们学习的；D.B 和C。

3.在这档节目中，你最喜欢的人是A.邓超；B.陈赫；C.李晨；D.杨颖；E.王祖蓝；F.其他。

然后，学生们带着调查任务和调查内容，与小组成员一起走进校园中，选择高一、高二和高三学生，有针对性地进行调查，记录调查结果，使用所学内容分析结果。

在体验整个活动的时候，学生们有效地应用数学所学，通过解决问题，增强对随机抽样的理解。同时，不少学生通过完成这样的作业，形成了数学应用意识，便于今后自主地在生活中应用数学，切实提高数学应用能力。

综上所述，应用问题导学模式实施高中数学教学，可以在改进传统教学模式的同时，提高课堂教学效果。所以，教师在实施高中数学教学的时候，可以以“巧设问题——提出问题——点拨引导——探究问题——解决问题——拓展问题”这样的路径为切入点，根据教学需要，应用多样的策略引导学生们与“问题”互动，通过自主、合作、探究，解决问题，掌握数学知识，锻炼问题解决能力，提高数学学习效果。