基于遗传模糊控制的风电机组偏航系统疲劳载荷研究

李忠信， 王大龙， 庄佳才， 刘志恒， 姚 琦， 周振波

（1.南方海上风电联合开发有限公司，广东珠海 519080；2.中国能源建设集团广东省电力设计研究院有限公司，广州 510663；3.暨南大学能源电力研究中心，广东珠海 519070）

风能作为一种清洁的可再生能源，对“双碳目标”的实现具有关键作用［1-2］。随着风电装机容量的快速增加，机组层面的优化运行控制已显现出重要的研究价值［3］。

偏航系统作为风电机组的重要组成部分，在风向发生变化时控制机舱转动以实现风轮对风［4］。传统的偏航系统优化控制聚焦于提升偏航精度，涵盖先进偏航控制算法［5-7］和偏航系统硬件设计［8］等领域。然而，由于风向的随机性，偏航系统需频繁进行对风操作，长期的启停循环会导致偏航轴承持续承载，引起机械结构疲劳损伤，间接增加发电成本［9］。因此，有必要在偏航系统的控制过程中考虑疲劳载荷的抑制［10］。

在偏航系统疲劳载荷抑制领域，已有学者对偏航系统疲劳载荷的影响因素和相应的优化控制进行了研究。针对偏航系统疲劳载荷的影响因素，Zhao等［11］研究了偏航速度和偏航压力对机组偏航系统疲劳载荷的影响。刘为等［12］进一步考虑了不同空气密度、湍流强度和平均风速等因素对偏航轴承、叶根和轮毂等部件疲劳载荷的影响。Xu［13］研究了不同偏航角度对偏航系统疲劳载荷的影响。上述研究考虑了不同因素与风电机组偏航系统疲劳载荷的耦合关系，为进一步优化控制提供了一定的理论基础。

针对偏航系统疲劳载荷抑制的优化控制，Stubkier等［14］提出了一种液压软偏航结构，利用硬件结构的改进降低偏航系统的载荷。张家旗［15］提出了一种根据实际风况制定的变速偏航策略，达到抑制偏航系统疲劳载荷的目的。Stubkier等［14］和张家旗［15］针对偏航系统选择了不同的优化对象，均取得了一定的载荷抑制效果，但并未进行考虑疲劳机理的量化寻优，优化结果难以保证有效性。陈思等［16］提出了一种考虑启停载荷的偏航系统优化控制方案，在偏航系统疲劳损伤指标的基础上对启动阈值进行了寻优，以改善结构疲劳情况。但是陈思等［16］仅考虑了偏航的启停优化，未考虑运行过程中的优化。同时，在上述偏航优化控制过程中，遗传算法［15］、粒子群算法［16］和模糊控制［17-19］等先进算法均有在相关研究中应用，但目前针对偏航过程的优化控制参数主要依靠研究人员的经验得到，主观性明显，缺乏合理的参数选取方法。

基于以上研究现状，笔者从风电机组偏航系统疲劳载荷机理出发，分析偏航轴承各个力矩的作用，基于机理分析引入2种衡量偏航系统疲劳载荷的指标参数。依据前述偏航系统疲劳载荷的量化指标，在基于经验的模糊偏航控制器基础上，笔者设计了一种通过载荷指标量化寻优的遗传模糊偏航控制算法，并基于FAST［20］平台对不同工况下的偏航过程进行仿真分析，验证所提出的遗传模糊偏航控制算法的有效性。

1 偏航系统疲劳载荷分析

1.1 偏航系统结构

风电机组偏航系统由风向标、偏航控制器、偏航驱动电机、偏航液压制动器、扭缆保护装置、偏航计数器、传感器和放大器等构成［21］。偏航系统框图如图1所示。

图1 偏航控制系统框图Fig.1 Block diagram of the yaw control system

1.2 偏航系统疲劳载荷表征参数

图1所示偏航系统运行过程中，风轮上的载荷与机舱的重力载荷会传递至偏航机构。载荷以力矩形式作用于偏航系统，主要表现在偏航轴承滚动力矩（M x）、偏航轴承俯仰力矩（M y）、偏航轴承偏航力矩（M z）3个维度，如图2所示。其中，M x与M y会改变偏航机构偏航爪与偏航齿圈的正压力，以此改变偏航爪上下表面的摩擦力。

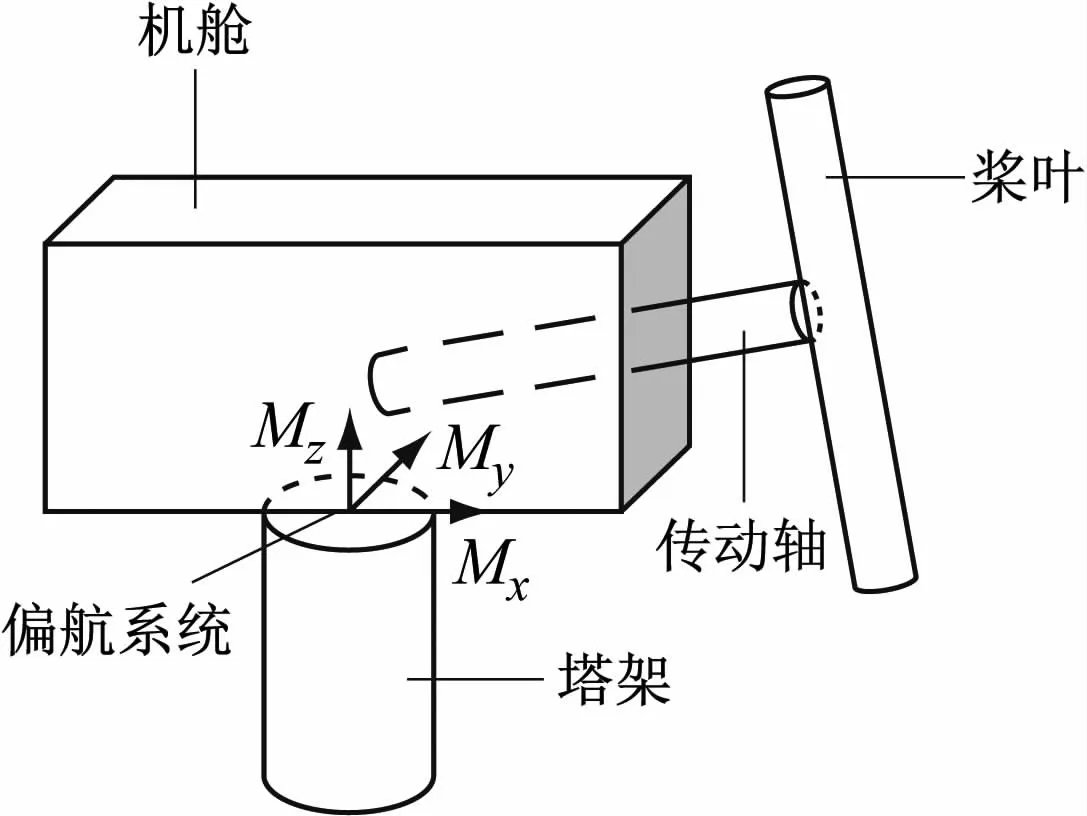
图2 偏航系统坐标系Fig.2 Yaw system coordinates

考虑到偏航系统的疲劳损伤是由于大量瞬态冲击的长期累积而产生的，在研究偏航系统疲劳载荷时将同时考虑疲劳的累积情况和单次偏航的瞬态冲击情况，计算前述力矩的等效损伤载荷（DEL，Damage Equivalent Load）［22］和最大瞬态冲击（MTI，Max Transient Impact）。

（1）等效损伤载荷（DEL）

DEL是材料力学中衡量机械结构累积疲劳损伤的一个重要指标。根据载荷时间序列，通过雨流计数法和Miner定理，DEL计算方法如下：

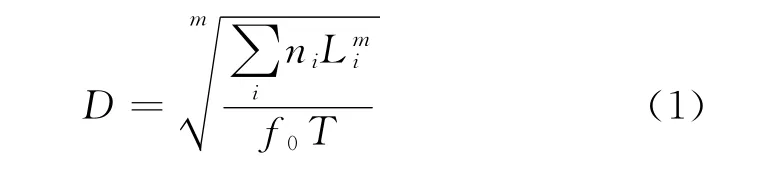
式中：L i为第i级的载荷；ni为第i级的雨流循环次数；m为疲劳指数，与结构部件材料相关；f0为等效循环载荷的循环率；T为载荷施加的总时间。

下文用D Mx、D My和D Mz分别表示力矩M x、力矩M y和力矩M z的等效损伤载荷。

（2）最大瞬态冲击（MTI）

由于风向的不确定性和湍流风的影响，偏航系统频繁启动制动，会对偏航轴承外齿圈产生剧烈冲击，这种瞬态冲击较其他时段的载荷影响更明显，应当采用适当的控制方法来抑制这种瞬态冲击，保护偏航系统。偏航系统的最大瞬态冲击可以用M x、M y和M z3个偏航轴承力矩在一段时间内各自的最大瞬态变化量来描述，即：

式中：M Mx、M My和M Mz分别为M x、M y和M z在时间t1至t2内相邻采样点差值绝对值的最大值。

1.3 FAST偏航系统模型

为研究风电机组偏航系统疲劳损伤特性，笔者以NREL 5 MW机组为研究对象，利用FAST平台设计风电机组偏航实验。机组主要参数见表1［23］。

表1 NREL 5 MW机组参数Tab.1 NREL 5 MW unit parameters

为了描述风电机组整体的动力学特性，FAST一共设置了17个自由度，通过设置这些自由度，FAST可以模拟塔筒的前后俯仰、偏航系统的左右转动、叶片运行的扭转和弯曲等。将Simulink接口与FAST相连接，可以利用Simulink设计控制器。FAST在Simulink中的模块如图3所示。

图3 FAST平台仿真界面Fig.3 FAST platform simulation interface

2 经验模糊控制器设计

2.1 整体设计

基于现有研究可知，风速、偏航角度偏差和偏航速度等对机组偏航系统的疲劳载荷均有影响，而偏航速度为唯一可控变量。因此，利用模糊控制算法设计考虑载荷抑制的偏航控制器时，输入变量可选风速和偏航角度偏差，输出变量选偏航系统的偏航速度。图4为所设计的模糊控制系统框图。其中，e为机组偏航角度与实际风向之间的偏差；w为风速；E和W分别为反映偏航角度偏差和风速的模糊量；V为输出变量，即偏航速度的模糊量；v为偏航速度的精确量，即经过偏航模糊控制器计算得出的最终风电机组偏航速度。

图4 模糊控制系统框图Fig.4 Block diagram of the fuzzy control system

2.2 隶属度函数与模糊规则

根据风电机组的运行工况，笔者所设计的经验模糊控制器假设偏航角度偏差在30°（0.523 6 rad）以下，偏航速度控制在0.8（°）／s（0.014 rad／s）以下，风速则在25 m／s以下。由此可设置如表2和图5所示的模糊控制器隶属度函数μ。其中，表2提供了输入输出变量的基本论域和模糊语言变量的设置；图5提供了输入输出变量隶属度函数图，均采用三角隶属度函数。

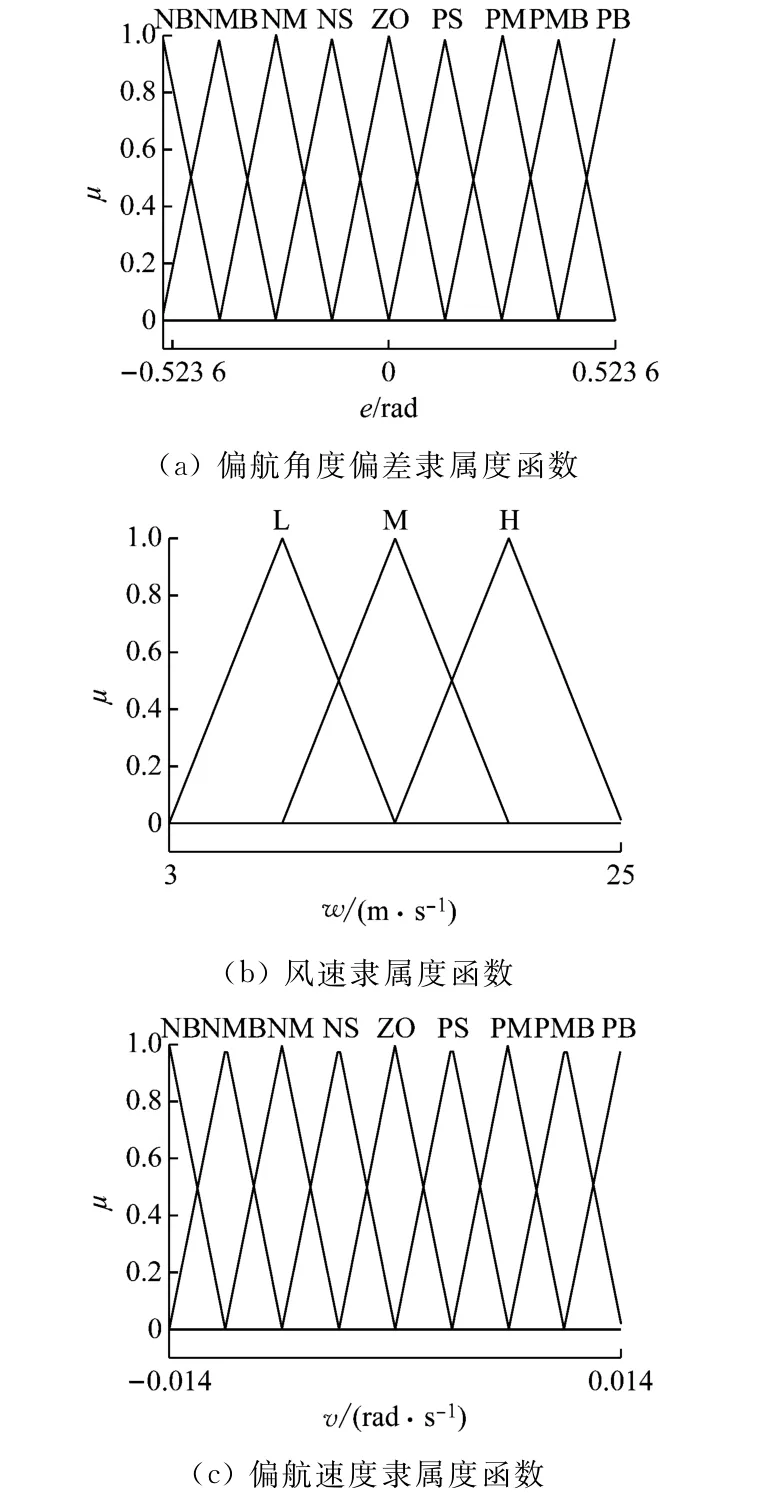
图5 模糊控制器隶属度函数Fig.5 Membership function of fuzzy controller

表2 基本论域和模糊语言变量Tab.2 Basic domain and fuzzy linguistic variables

为了达到抑制载荷的效果，传统的模糊偏航控制算法在偏航角度偏差小、风速低的工况下降低偏航速度，以柔化偏航系统的动作。基于这一思想，可设置表3所示的经验模糊控制规则。

表3 根据经验的模糊控制规则Tab.3 Fuzzy control rules based on experience

2.3 模糊控制输出

对模糊输出量V利用面积重心法［24］进行精确化，即可得到精确的偏航速度v。至此，完成了经验模糊控制器的整体设计。

3 遗传模糊控制优化的偏航系统

基于经验的模糊控制器在控制规则上依赖运行人员的主观判断，无法保证对偏航系统疲劳载荷的准确抑制。因此，本节将利用第1.2节中所提载荷指标作为优化目标，基于遗传算法对偏航模糊控制规则进行优化。基于遗传算法优化的模糊控制框图如图6所示。

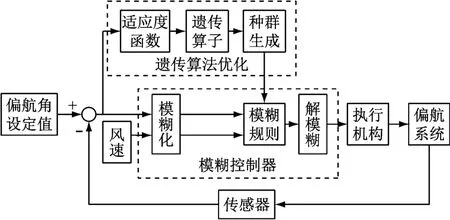
图6 基于遗传模糊控制的偏航系统Fig.6 Yaw system based on genetic fuzzy control

根据图6，首先生成规定数量的初始种群（即初始模糊规则），并输入到模糊控制器，然后再利用遗传算法对模糊规则进行寻优。当得到最优的模糊规则后，再根据输入变量进行模糊判决，最后经过解模糊后得到最优偏航速度。

3.1 编码

采用运算效率较高的实数编码方式［25］，即NB、NMB、NM、NS、ZO、PS、PM、PMB、PB分别编码为1～9。对于第2节中所建的经验模糊控制器，模糊控制规则可以用长度为3×9=27的染色体表示。如表3中的经验模糊规则可进行如下编码：

3.2 适应度函数选择

为了达到抑制偏航系统疲劳载荷和快速对风的目的，采用前文引入的载荷表征参数M Mx、M My、M Mz、D Mx、D My、D Mz和时间积分绝对误差（I）作为适应度函数的优化量。适应度计算方程设置如下：

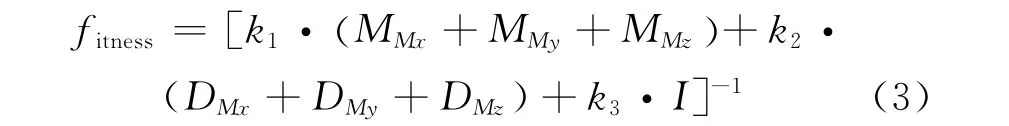
式中：k1、k2和k3均为权重系数，后续仿真中k1取1，k2取0.08，k3取0.03。

D Mx、D My、D Mz根据式（1）进行计算，M Mx、M My、M Mz根据式（2）进行计算，I的计算式如下：

式中：t为当前时间；e（t）为当前偏航角度与期望偏航角度之间的偏差值。

3.3 选择、交叉、变异

选择操作采用转盘式选择算子［26］，首先通过式（5）计算得到第i个个体的选择概率P i，再由此概率决定第i个个体是否被选择。为防止最优个体在选择操作中丢失，每一代适应度最高的个体会直接遗传到下一代。

式中：f i为变异个体的适应度。

为了提高全局搜索能力和避免早熟现象，采用自适应调整交叉概率和变异概率的方法［27］。自适应调整交叉概率Pc和自适应变异概率Pm如下：

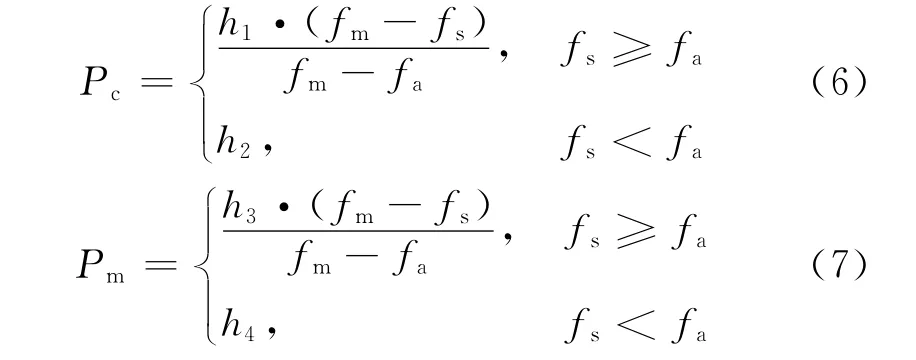
式中：fm为最大适应度；fa为平均适应度；fs为交叉个体中较大的适应度；h1取0.5；h2取0.9；h3和h4均取0.1。

3.4 优化结果

针对模糊偏航控制系统，取遗传算法的种群数量为40，迭代次数为50，进行模糊控制规则的寻优。适应度函数进化曲线如图7所示。优化后的模糊控制规则见表4。

图7 适应度函数收敛图Fig.7 Convergence graph of fitness function

表4 优化后的模糊控制规则Tab.4 Optimized fuzzy control rules

4 算例分析

基于FAST／Simulink软件，对NREL 5 MW风电机组偏航系统疲劳载荷在不同工况下的情况进行分析。以经典恒速控制策略（限速0.3（°）／s和0.8（°）／s）和经验模糊控制策略作为对照组，设置表5所示的不同稳态风速、湍流强度和偏航角度工况，验证所提出的遗传模糊偏航控制器的偏航系统疲劳载荷抑制效果。

表5 工况参数统计Tab.5 Working condition parameter table

4.1 工况1载荷情况分析

工况1为稳态风，风电机组在4种不同偏航控制策略下的偏航情况如图8所示，对应的风电机组偏航轴承力矩情况如图9所示。由图8和图9可以看出，4种策略均能有效跟踪偏航角度，而采用模糊控制的2种策略在跟踪过程中更加平滑，偏航轴承力矩波动较不明显。

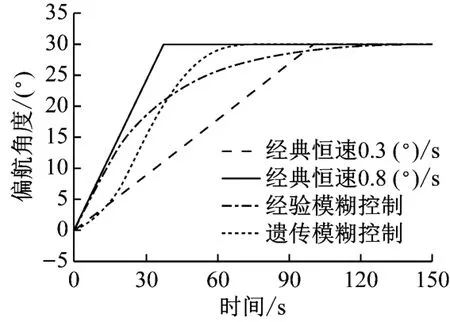
图8 工况1偏航角度时域曲线Fig.8 Time domain curves of yaw angle in condition 1

表6给出了量化计算得到的工况1偏航系统疲劳载荷参数。由表6可知，遗传模糊控制对于抑制MTI效果明显，其中，遗传模糊控制的M Mx分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了53.07%和83.58%，比经验模糊控制减小了85.62%；遗传模糊控制的M My分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了4.94%和18.59%，比经验模糊控制减小了21.21%；遗传模糊控制的M Mz分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了47.69%和80.91%，比经验模糊控制减小了82.76%。遗传模糊控制的D Mx分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了2.85%和3.72%，比经验模糊控制减小了6.08%；遗传模糊控制的D Mz分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了7.74%和56.59%，比经验模糊控制减小了50.71%；但遗传模糊控制会使D My增大，分别比0.3（°）／s和0.8（°）／s经典恒速控制增大了2.3%和6.25%，比经验模糊控制增大了5.29%。总体上，所提出的遗传模糊控制在开始和结束偏航时刻均不会产生大的瞬态冲击，而3种对比方案分别会在开始和结束时刻产生明显的瞬态冲击，遗传模糊控制在稳态风工况下显示出明显的载荷抑制效果，这一结果也与图9呈现的偏航轴承力矩波动情况相符。

图9 工况1偏航轴承力矩时域曲线Fig.9 Time domain curves of yaw bearing torque in condition 1

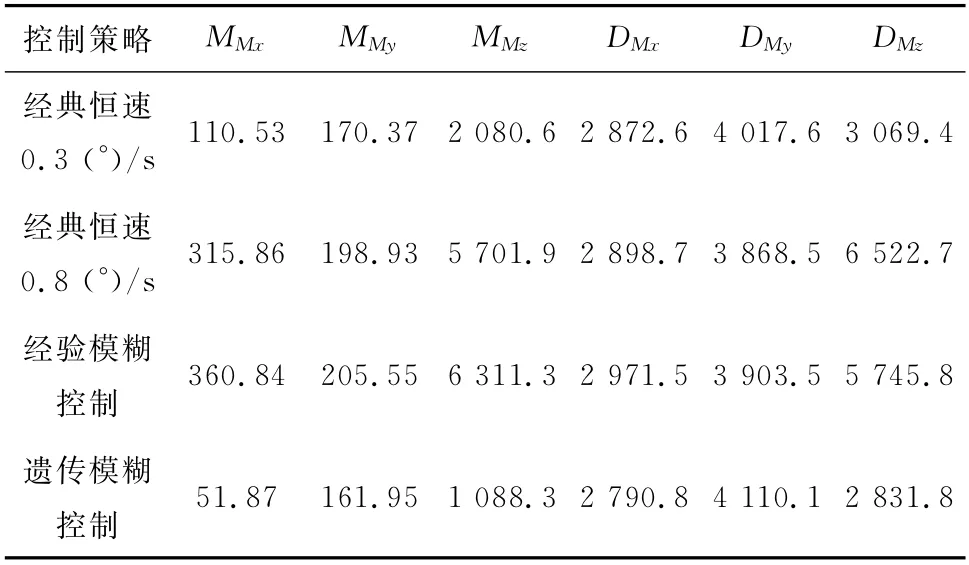
表6 工况1偏航系统疲劳载荷对比Tab.6 Comparison of fatigue load of yaw system under condition 1 k N·m

为了描述机组偏航过程中的有功功率，笔者计算了150 s偏航仿真实验过程中4种控制策略下的平均功率，结果如表7所示。由表7可知，所提出的遗传模糊控制的平均功率比经验模糊控制下降1.2%，比0.8（°）／s经典恒速控制下降了1.1%，比0.3（°）／s经典恒速控制则上升了2.5%。可以看出，所提出的遗传模糊控制在考虑传动系统疲劳载荷抑制的基础上对偏航动作进行了柔化，导致一定的功率损失。但综合考虑，所提出的遗传模糊控制造成的功率损失明显较小，而对偏航系统疲劳载荷的抑制效果更为显著。

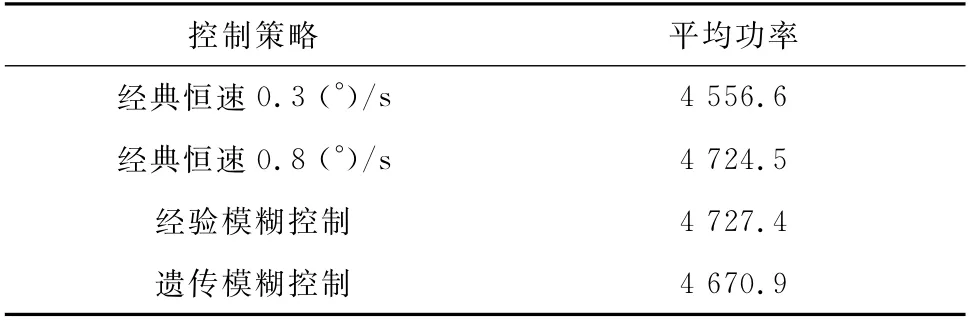
表7 工况1平均功率对比Tab.7 Comparison of mean power under condition 1 kW

4.2 工况2载荷情况分析

工况2模拟的情景为湍流风，风速时域曲线如图10所示。4种不同控制策略的偏航角度随时间变化的情况如图11所示，相应的风电机组偏航轴承力矩如图12所示。载荷计算结果如表8所示，平均功率的对比如表9所示。

图10 工况2湍流风速时域曲线Fig.10 Time domain curves of turbulent wind speed in condition 2

图12 工况2偏航轴承力矩时域曲线Fig.12 Time domain curves of yaw bearing torque in condition 2

由图11可知，湍流风工况下4种控制策略均能有效跟踪偏航角度，满足偏航精度要求。而从表8可知，在湍流风工况下，遗传模糊控制可以较好地抑制M Mz和D Mx、D Mz的数值。其中，遗传模糊控制的M Mx分别比0.8（°）／s经典恒速控制和经验模糊控制减小了51.69%和57.82%，但比0.3（°）／s经典恒速控制增大了30.2%；M Mz分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了73.29%和90.03%，比经验模糊控制减小了91.24%；D Mx分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了0.09%和6.18%，比经验模糊控制减小了3.48%；D Mz分别比0.3（°）／s和0.8（°）／s经典恒速控制减小了5.83%和95.89%，比经验模糊控制减小了20.64%。相比之下，本文所提出的遗传模糊控制在湍流风工况下对M My和D My的抑制效果不理想，主要是由于湍流风工况下偏航系统的俯仰动态难以通过改变偏航速度进行调节。

表8 工况2偏航系统疲劳载荷对比Tab.8 Comparison of fatigue load of yaw system under condition 2 kN·m

图11 工况2偏航角度时域曲线Fig.11 Time domain curves of yaw angle in condition 2

由表9可以看出，与稳态风工况下的平均功率结果相似，湍流风工况下采用遗传模糊控制的机组平均功率比采用经验模糊控制降低1.4%，比0.8（°）／s经典恒速控制降低1.2%，但比0.3（°）／s经典恒速控制上升1.6%。因此，在湍流风工况下，采用遗传模糊控制同样产生了较小的功率损失。综合考虑，所提出的遗传模糊控制在更接近实际风况的湍流风工况下也展现出良好的偏航系统载荷抑制效果。

表9 工况2平均功率对比Tab.9 Comparison of mean power under condition 2 kW

5 结 论

（1）根据偏航系统运行机理引入2种疲劳载荷表征参数，综合考虑了累积损伤和瞬时极限损伤的影响，用于指导优化控制器设计。

（2）在经验模糊控制基础上，利用遗传算法优化模糊控制规则，有针对性地设计了一种遗传模糊控制，获得最优偏航速度。

（3）在稳态风工况下，遗传模糊控制对于抑制偏航轴承的MTI和DEL效果显著，其中M Mx和M Mz相比恒速控制和经验模糊控制策略大幅度下降40%以上，DEL也有所下降；在湍流风工况下，遗传模糊控制对偏航轴承的MTI和D Mz有较好的抑制效果，其中M Mz相比恒速控制和经验模糊控制策略下降70%，D Mz相比恒速控制和经验模糊控制策略下降5%以上。

（4）所提出的遗传模糊控制对风电机组偏航系统的载荷抑制具有明显效果，对于降低偏航系统损耗和提升风电机组运行经济性具有一定的现实意义。