SOFC阳极尾气循环进气系统特性建模与流量控制方法

熊星宇， 薛振忠， 武 鑫， 畅雨薇

（华北电力大学能源动力与机械工程学院，北京 102206）

固体氧化物燃料电池（SOFC）是一种全固态结构的燃料电池，具有燃料适用范围广、能量利用率高、高效清洁等特点。在能源和环境矛盾日益尖锐的当今社会，固体氧化物燃料电池成为世界各国争相开发的新一代能量转换技术。固体氧化物燃料电池发电系统主要由燃料电池电堆、阴极进气系统、阳极进气系统、水热管理系统和电控系统等组成［1］。其中阳极进气系统为电堆内的电化学反应提供燃料气，对电堆的电化学反应速度、温度、工作效率、阴阳极之间的压力、寿命与安全等具有重要的影响，是固体氧化物燃料电池发电系统中一个重要的子系统，对系统的高效、稳定运行具有重要作用。

从满足并网需求、运行成本与寿命等角度来说，需要严格控制阳极进气，使发电系统维持高效稳定运行。Qi等［2］针对外界电流干扰的情况下，为维持电堆电压稳定，设计了一种比例-积分-微分（PID）控制器，通过调节氢气流量使电堆电压维持在稳定值。Ferrari［3］提出了前馈与标准PID结合的控制方法，该方法能有效避免干扰电流对电堆温度、电压和寿命的影响。Li等［4］基于建立的关于电堆的支持向量机模型，提出一种基于数据驱动的非线性控制方法，可通过控制阳极进气有效地应对外界干扰。综上所述，阳极进气对维持电堆稳定运行具有重要意义，而阳极尾气循环作为阳极进气系统的一部分，同样也需要严格控制。阳极废气再循环有利于避免重整器积碳，防止燃料电池热裂；废气再循环也可使系统在更宽的温度范围内安全运行，同时提高燃料利用率［5］。

SOFC阳极进气系统的控制是一个复杂的问题，内部参数之间、外部不确定因素之间以及内外部参数之间都具有强耦合性，这就对SOFC阳极进气系统的控制提出了较高的要求，常规的控制策略性能有限，需要一个精准且可靠的系统模型来实现其性能优化和控制。甚至为了解开参数与子系统之间的耦合性，需要分别对子系统的核心部件进行建模与控制［6］。

阳极尾气循环进气系统对整个SOFC发电系统的高效、稳定运行有重要影响。阳极尾气一般有2种循环方式：喷射器和气体压缩机（泵）［7］。由于喷射器的操作条件要求较高，较小的偏差便会使整个喷射器系统性能显著降低，因此常使用气体压缩机（泵）作为尾气循环的核心部件［8］。爪式泵因其高可靠性、结构简单、紧凑和无油而被广泛应用于燃料电池［9］。此外，由于爪式泵具有内置压缩功能，与罗茨鼓风机相比，高压比下的容积效率得到了优化，同时具有结构简单和高可靠性的优势［10］。因此，爪式泵在燃料电池中有广阔的应用前景［11］。

爪式泵作为阳极尾气循环进气系统的核心部件，对其进行特性建模与流量控制研究至关重要，而目前针对爪式泵的研究相对来说还较少。Gu等［12］利用神经网络方法，选择容积效率和轴功率2个重要因素作为神经网络的输入因子，并采用仿真数据训练神经网络来预测爪式泵的性能，可用于燃料电池系统爪式泵的设计和选择。Giuffrida［13］建立了爪式泵的完整数学模型，并分析了2个不同形状参数的爪型对爪式泵性能的影响。崔冬等［14］建立了光滑的弯曲转子型线和光滑的直转子型线的爪式泵数学模型，并比较了这2种转子型线的爪式泵的工作性能和机械性能。武涛等［15］提出了一种新型螺旋无尖点爪式转子结构，并将其抽气性能与传统爪式转子进行了比较，仿真结果表明，所提出的螺旋转子具有更好的机械性能和更高的抽气效率。然而，以上针对爪式泵的特性研究多侧重于描述爪式泵的内部结构，较少分析基于运行数据的爪式泵特性建模与控制策略，不利于实际应用。

笔者针对固体氧化物燃料电池系统中的阳极尾气循环进气系统开展研究，首先搭建了20 k W级SOFC发电系统的阳极尾气循环进气系统模拟实验台，然后基于支持向量回归（SVR）方法建立核心部件爪式泵的特性模型，并提出了基于模型预测的阳极尾气循环进气系统流量控制方法，最后通过实验验证了该控制方法的有效性。

1 阳极尾气循环进气系统模拟实验台搭建与测试

阳极尾气循环进气系统作为阳极进气系统的一部分，对于预防积碳、提高燃料利用率等具有重要的作用。笔者从实际需求、运行安全与成本等角度出发，搭建了一个模拟实验台，研究SOFC阳极尾气循环进气系统。模拟实验台主要由鼓风机、爪式泵、阀门、管道和各类传感器等组成。

1.1 阳极尾气循环进气系统模拟实验台

基于20 k W级SOFC发电系统搭建的阳极尾气循环进气系统模拟实验台的流程图和实物图分别如图1和图2所示，其中Ti（i=1～5）代表温度传感器，Pi（i=1～5）代表压力传感器，Fi（i=1，2）代表流量传感器。

图1 SOFC阳极尾气循环进气系统模拟实验台流程图Fig.1 Flow chart of the emulation testbed of SOFC anode tail gas circulation intake system

图2 SOFC阳极尾气循环进气系统模拟实验台实物图Fig.2 Real diagram of the emulation testbed of SOFC anode tail gas circulation intake system

如图2所示，鼓风机为整个系统提供进气；精小型调节阀是一种差压式调节阀，用来模拟实际气体经过电堆后的压降；球阀与气动阀都可以改变管道口径大小，用于模拟不同负载工况；爪式泵是整个系统的核心部件，可以将部分尾气抽回，再重新加压循环回阳极进气系统。在爪式泵的进出口处分别配置了温度和压力传感器，在出气处配置了涡街流量计。

本实验台的通信方式有CAN线通信和RS485通信2种，除爪式泵外，其余设备均为RS485通信，上位机软件为Labview2018。数据采集模块可以根据采样周期将显示的数据写入Excel表，用于后续的实验分析。在系统运行过程中，爪式泵的转速控制、气动阀开度、各类传感器数据读取和保存等操作，整个通信需要0.5 s。因此，将采样周期根据运行时间设置为0.5 s。

本实验台采用Busch公司的MA0018A型爪式泵，内置PI转速闭环控制。通过测试发现速度闭环快速且稳定，上位机软件给予爪式泵数字信号就可以达到相应的转速要求。根据20 k W级SOFC发电系统的设计要求，同时以H2与CO混合气的燃料进气（其中CO与H2体积比V（CO）∶V（H2）=1∶4）为例，标准状况下进气的体积流量一般在10～14 m3／h，本实验以空气为模拟燃料气，为了模拟实际进气时燃料的体积流量，管路内的压力均在40 k Pa以下，在实际运行过程中，阳极尾气在流经爪式泵前的温度一般已降至40～80℃，因此MA0018A型爪式泵的技术参数可以满足本实验的需求。

1.2 爪式泵流量特性测试实验

1.2.1 实验条件及工况设置

根据20 k W级电堆实际测试实验的进气量，计算得出模拟实验台中鼓风机进气量设置为12 m3／h即可满足实际需求，鼓风机通过PID控制器可以将流量稳定在某一设定值。以V（CO）∶V（H2）=1∶4混合气为燃料气，以燃料利用率为85%为例［16］，为保证有足够的水蒸气参与置换反应［17］，尾气的循环率应在30%以上，通过计算可得循环尾气体积流量最低为4 m3／h左右，因此爪式泵应提供4 m3／h以上的流量数值，对应转速应超过1 300 r／min。考虑到系统运行安全和在实际运行过程中可能会出现的管路负载变化，将球阀划分为4个开度（90°、67.5°、45°和22.5°），气动阀划分为4个开度（20 m A、16 m A、12 m A和8 m A），模拟了爪式泵在16种负载工况下的运行状态，爪式泵转速以100 r／min为间隔从1 300 r／min至4 000 r／min变化，测试了爪式泵在全转速、全工况情况下的运行特性。具体的实验环境条件见表1。

表1 实验工况Tab.1 Experimental condition

实验过程中，先设置鼓风机流量、球阀开度和气动阀开度，然后改变爪式泵转速，记录不同转速下爪式泵的流量特性和相关参数。采集的数据均为爪式泵稳定状态下的数据，共获得500组有效数据。

1.2.2 实验数据分析

爪式泵转速-流量-压比的关系如图3所示。从图3可以看出，爪式泵的流量特性整体与转速成正比、与压比成反比，符合流体机械的一般特性。但从图3也可以看出，数据点之间并不光滑，这与爪式泵流量的非线性特性有关，再考虑到进口温度和湿度对爪式泵的影响，其特性呈现出复杂的非线性。

图3 爪式泵转速-流量-压比关系图Fig.3 Speed-flow-pressure ratio diagram of claw pump

爪式泵在开环状态下的动态流量特性如图4所示。从图4可以看出，从转速指令下达到有流量输出，系统存在4 s的时间延迟，需要在后续控制器的设计中补偿此时间延迟。爪式泵在稳定状态下的流量存在大约设定值2%的波动范围，这是因为爪式泵在工作时具有一定的振动和噪声。而振动和噪声的产生是因为爪式泵与齿轮泵的结构类似，都存在脉动现象，在实际操作环境中很难避免此现象的发生。基于以上研究可以发现，爪式泵流量特性具有强非线性、大迟滞性和复杂性。

图4 爪式泵开环条件下转速与流量的动态特性Fig.4 Dynamic characteristics of speed and flow rate of claw pump under open-ring condition

2 爪式泵特性建模方法与流量控制方法

爪式泵内部结构复杂，可以采用运行数据建模方法建立高效、简便、准确的爪式泵特性模型，以用于流量控制策略研究。因此，基于运行数据，通过支持向量回归方法开展爪式泵特性建模，同时基于此特性模型提出了一种基于模型预测的流量控制策略。

2.1 SVR方法简介

支持向量机（SVM）是一种基于边距的按监督学习的方式对数据进行分类的机器学习方法［18］。SVM相对于其他传统的机器学习方法具有较强的适应性和泛化能力，在系统故障分析和状态预测等方面越来越受到人们的关注［19］。基于以上特点，笔者选用SVM数据建模的方法。其基本模型是定义在特征空间上的间隔最大的线性分类器，间隔最大使其有别于感知机；SVM还包括核技巧，这使其成为实质上的非线性分类器，SVM的学习策略就是间隔最大化，可形式化为一个求解凸二次规划的问题。

如图5（其中X、Y为坐标轴）所示，SVM学习的基本想法是求解能够正确划分训练数据集并且几何间隔最大的分离超平面。wT·x+b=0即为分离超平面，其中w和b分别为分离超平面的法向量和截距，x为样本，对于线性可分的数据集来说，这样的分离超平面有无穷多个（即感知机），但是几何间隔最大的分离超平面却是唯一的。分离超平面关于所有样本点的几何间隔即所谓的支持向量到分离超平面的距离。

图5 支持向量机结构图Fig.5 Structure of support vector machine

对上述公式使用拉格朗日乘子法计算可得到其对偶问题。对每个约束条件加入拉格朗日乘子，则有：

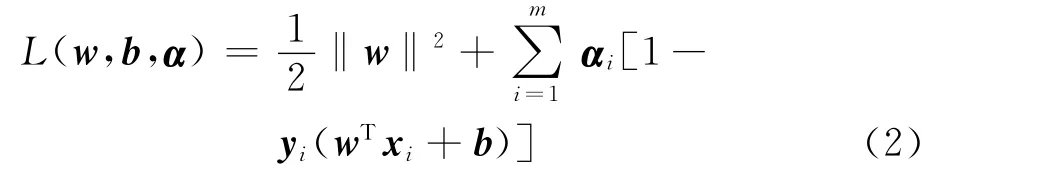
式中：L（w，b，α）为拉格朗日函数；αi为拉格朗日乘数；α为拉格朗日乘子向量。

根据式（2）分别对w和b求偏导，令偏导为0，可得：

约束条件为：

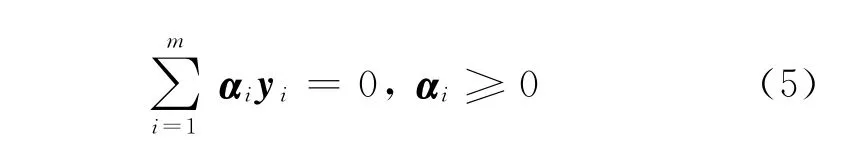
对式（5）关于α求导，求出w和b，得到最终的模型：

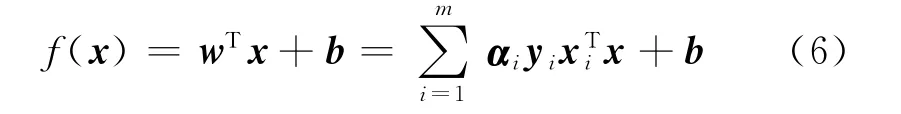
式中：f（x）为点到分离超平面的距离。

SVR是SVM的一种运用，除了一些细微的区别，两者的基本思路一致。使用SVR进行回归分析时，与SVM一样，都需要找到一个分离超平面，不同的是：在SVM中是要找出一个间隔最大的分离超平面，而在SVR中，定义图5虚线内区域的数据点的残差为0，虚线区域外的数据点（支持向量）到虚线边界的距离为残差，其训练的目的就是使这些残差最小。SVR就是要找出一个最佳的条状区域（虚线内区域），再对区域外的点进行回归［20］。

在实际应用中，允许支持向量机在一些样本上出错，为此引入了松弛变量，同时针对非线性模型，又引入了核函数的思想，有关于求内积的问题都可以考虑使用核函数来计算，常用的核函数有线性核、多项式核和高斯核［21］。高斯核函数能够实现非线性映射，相较于多项式核函数参数较少，模型复杂程度更低。因此，笔者选用高斯核作为核函数映射［22］。

2.2 爪式泵特性模型构建

如图3所示，爪式泵在全转速情况下会出现流量过大的情况，与实际应用不符，故在数据建模之前首先进行了数据筛选，只针对满足实际需要的数据进行建模，筛减后共380个数据。

爪式泵特性建模的流程如图6所示，输入特征为转速、进出口温度及进出口压力5个特征，输出特征为流量。将数据集中的80%作为训练数据、20%作为测试数据，开展模型训练与测试，测试结果如图7所示。

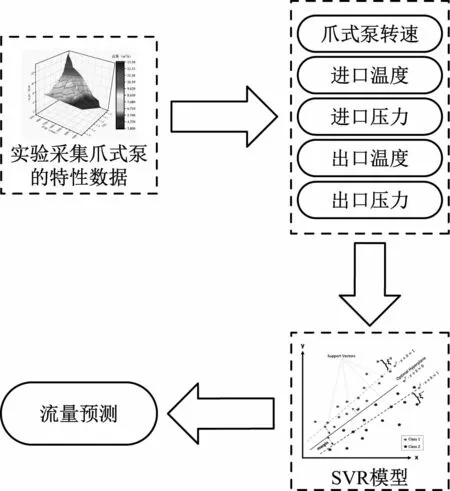
图6 爪式泵SVR特性建模流程图Fig.6 Flow chart of SVR characteristic modeling of claw pump

评价一个回归模型好坏的指标一般有决定系数（R2）、均方根误差（eRMSE）和平均绝对误差（eMAE）。3个指标的具体计算公式如下：

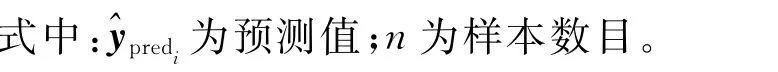
R2可用来表示预测模型的精度，其值越接近于1表明模型的预测精度越高，eRMSE和eMAE的值越小，表明模型的预测能力越强［22］。

考虑到传感器精度，设定流量预测的允许误差为±5%以内。由图7可得，输出流量测试误差（eti）均在允许的误差范围内，R2为0.999 583 081，eRMSE为0.140 310 195，eMAE为0.112 241 166，模型计算时间为0.089 3 s。因此，所建模型满足实际实验需求，可以用于爪式泵流量特性的预测以及控制策略的研究。其中测试误差由式（10）计算得到：

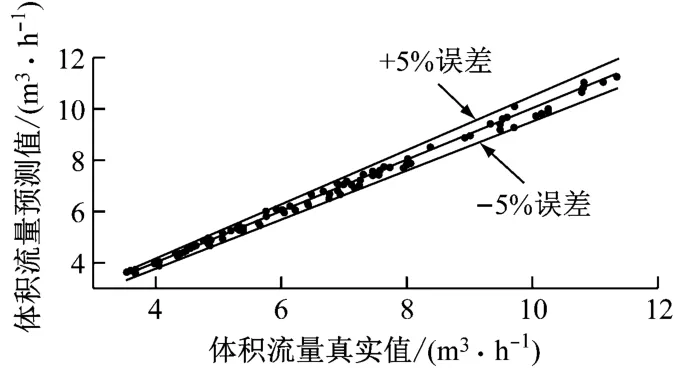
图7 SVR模型测试结果Fig.7 Test results of SVR model

为了实现SOFC电堆高效、稳定运行，在应对干扰电流时，一般希望其能够维持输出电压稳定，这就需要通过调节阳极尾气循环进气系统的流量来达到此目标。因此，提出了基于模型预测的流量控制方法，保证该系统在应对外界干扰时有良好的动态流量跟踪性能。

2.3 Smith预估算法

基于前文爪式泵开环状态下的动态特性测试，可以发现该系统存在较大的时间滞后现象。对于纯滞后系统，Smith预估算法是一种简单而有效的算法［23］。Smith预估算法的结构图如图8所示，其中R（s）为目标值，E（s）为反馈误差，U（s）为控制器输入，Ys（s）为系统反馈补偿值，Y（s）为系统输出值，Gc（s）表示控制器传递函数，Gp（s）和e-τps分别表示被控对象无延迟部分和纯延迟因子，Gm（s）和e-τms分别表示被控对象无延迟部分和纯延迟因子的预估模型，Gm（s）（1-e-τms）为Smith预估器传递函数。

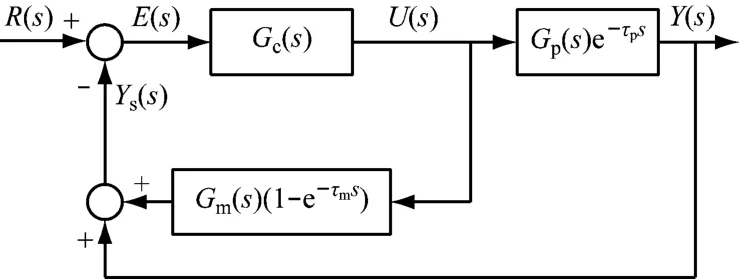
图8 Smith预估算法基本结构图Fig.8 Basic structure of Smith's prediction method

当Gp（s）=Gm（s），e-τps=e-τms时，Smith预估器就可以完全消除系统中存在的纯滞后现象。但是当Smith预估器参数与被控制对象不完全匹配时，系统会出现不稳定渐扩振荡。

2.4 基于模型预测的流量控制方法

PID控制因其稳定性高、算法简单和动态响应快等优点而被广泛应用于如今的工业控制中。由于爪式泵是一个非线性极强的系统，因此采用PID控制方法或Smith预估器很难得到一个与爪式泵匹配度较高的线性传递函数，也很难用Smith预估器来消除系统中的纯滞后现象。

针对Smith预估器效果不理想的情况，Mo等［24］提出了一种基于隐马尔可夫模型的Smith预估器，通过离散隐马尔可夫模型和指数加权移动平均模型预测Smith预估器中的时间延迟，解决了时间延迟不匹配的问题，但是针对时滞对象模型不准确的情况并未提出解决方法。刘逢刚等［25］通过建立准确的数学模型来代替参数未定的系统无延时传递函数，拥有较好的控制效果。基于Smith预估器原理和上述研究，利用爪式泵特性模型预测爪式泵无延时部分的流量输出。因此，针对阳极尾气循环进气系统，提出了一种基于模型预测的PID流量控制策略，具体原理图如图9所示。

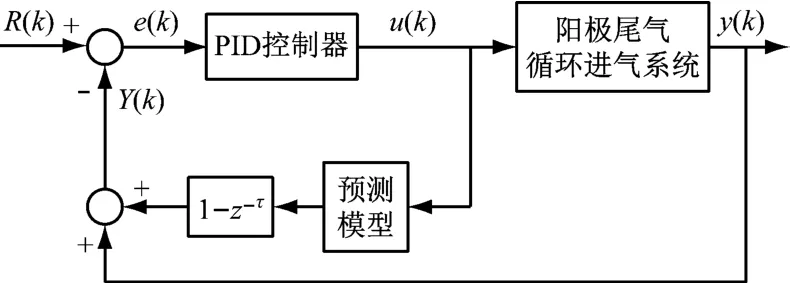
图9 基于模型预测的流量控制方法框图Fig.9 Schematic diagram of model predictive control method on flow rate

图9所示的预测模型为所建立的SVR流量预测模型，其中z-τ为本系统的时间延迟，R（k）为目标值，e（k）为误差，u（k）为控制输入，y（k）为系统输出值，Y（k）为系统反馈补偿值。

2.5 基于模型预测的流量控制方法验证

如上文1.1节所述，实验中的尾气循环最低体积流量设置为4 m3／h，并以此为起点追踪目标体积流量。实际工程中一般在起始阶段采用开环方法，使爪式泵快速达到性能比较平稳的阶段，以提高阳极尾气循环进气系统的响应时间。因此，在实验中当爪式泵的输出体积流量达到4 m3／h后，应采用所提控制策略来提高系统的性能。

本文中系统线性模型利用参数辨识方法获得，PID控制器参数采用Ziegler-Nichols整定法进行整定。实验结果如图10所示，PID和模型预测流量控制方法在三段流量跟踪的响应时间（达到2%稳态误差内的时间）和超调量对比如表2所示。

图10 基于模型预测和PID流量控制方法的跟踪曲线Fig.10 Tracking curve of flow rate by model predictive control and PID control methods

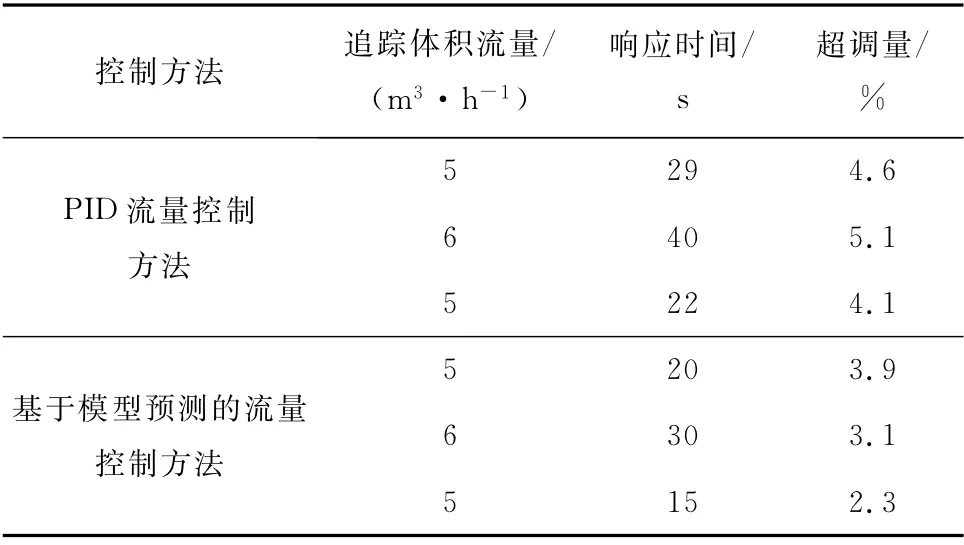
表2 2种控制方法跟踪参数对比Tab.2 Comparison of tracking parameters of two control methods

由于开环状态下系统存在2%的稳态误差，故设定该系统稳态误差为2%。由图10与表2可知，基于模型预测的流量控制方法的平均响应时间为22 s，平均超调量为3.1%；而PID流量控制方法的平均响应时间为30.3 s，平均超调量为4.6%。基于模型预测的流量控制方法的响应时间相对于PID流量控制方法更快，平均每段可减少8 s以上，同时超调量也有所减小，均在4%以下；PID流量控制方法的超调量均在4%以上，最大可达5.1%。因此，相对于PID流量控制方法，基于模型预测的流量控制方法拥有更好的流量跟踪性能，可以更好地满足实际应用。

3 结 论

（1）基于20 k W级SOFC发电系统，搭建了阳极尾气循环进气系统模拟实验台，对该系统的核心部件爪式泵开展了特性分析，发现其流量特性具有强非线性、大迟滞性和复杂性。

（2）基于SVR方法，提出了一种爪式泵的特性建模方法，并将其用于爪式泵流量特性预测。结果显示，模型输出流量预测误差均在允许的误差范围（±5%）内，证明了所提出的建模方法的准确性。

（3）根据上述模型，提出了一种基于模型预测的阳极尾气循环进气系统流量控制方法。实验结果显示，基于模型预测的流量控制方法的调节时间和超调量均小于PID流量控制方法。因此，该控制方法拥有更好的流量跟踪性能，能更好地满足实际应用。