小学拼图作业设计中数学联系的误区与对策

吴志健 江苏省宜兴市新建小学

小学用正方体拼图作业中的数学联系是丰富的，其中的部分联系在作业设计时必须凸显出来，绝不能可有可无。然而一些教师根据自己用正方体拼图的经验，以及对课本、补充练习册上相关作业题的习得，在作业中的学具操作、草图画法、计算方法上形成了自以为是的错误做法，而且这些错误做法隐蔽在学生“正确解题”里面不易觉察，亟需引起大家的关注。

一、书本“捆绑”，致使只是呈现图形，学生没有习得草图画法

书本是指数学课程标准、教科书、教学用书以及教育教学理论书籍。书本“捆绑”，是指教师根据自己对书本的误读通过作业习题去引导学生生成数学联系，其最为明显的特征是作业题情境与数学联系目标机械地割裂，在学生“正确解题”里弱化了作业功能。其最为典型的是用正方体拼图中的画草图问题。《义务教育数学课程标准（2022年版）》（下文简称《数学课程标准》）指出学生在第一学段（1-2年级）就要“会用简单的图形拼图，能在组合图形中说出各组成部分图形的名称”。［1］对于小学生而言，由长方形、正方形、三角形、平行四边形或圆拼成平面组合图形，可以使用方位词与图形名称简洁地描述出来，再根据“描述”来画出草图。但是，由正方体拼成不规则立体图形，怎样拼，拼成后是什么样子，学生很难用言语来表达清楚，也很难简单地与拼平面组合图形的草图画法建立数学联系。因此，在这类作业题中，常常直接给出拼成之后的不规则图形。而一些教师在设计作业时往往急功近利，不去设计提示语引导学生根据给出的不规则图形去描述拼成的样子，更不去设计不规则图形形成过程的图示引导学生探究如何画出草图。

例如，作业题：若干个棱长为1 分米的正方体纸盒放在墙角（如下图）（见图1），体积是（ ）立方分米，露在外面的面的面积之和是（ ）平方分米。

图1

学业一般的学生弄懂题意后，能够联系给出的图形，数出墙角的正方体纸盒共计6个，露在外面的面，共计12 个边长是1 分米的正方形，从而完成填空题。学业优秀的学生能够观察给出的图形，联系立体图形的三视图，根据三视图来算出题中露在外面的面的面积之和。这样设计，学生正确率高，教师自我满意度高，问题是，学生的空间观念并没有获得应有的发展。大家知道，“实物观察与描述、拼摆与画图”“都是发展学生空间观念的有效途径”。［2］也就是学生的空间观念需要通过多种数学联系去有效发展，仅仅依靠上述做法是远远不够的。

破解这种误区的对策有二：一是设计提示语。如，这些放在墙角的正方体纸盒有几层，上层有几个正方体，其中能在图中看到几个正方体；下层有几个正方体，其中能在图中看到几个正方体，为什么？这样的提示语，能够引导学生正确地看图、读图，从平面到空间进行转化，在无形之中“口述”给出的不规则立体图形。二是设计画草图的示意图。如，补充图2以及两个要求：（1）你能根据示意图，把图1画出来吗？试试看。（2）画出草图后，想一想：你是怎么画的，有什么经验？这样设计，就能够引导学生自己画草图，并归纳草图的画法，总结画图经验。虽然画这种图形的草图，对于小学生来讲是比较难的，但是，其对于学生发展几何直观素养是非常有效的。《数学课程标准》指出“根据语言描述画出相应的图形”是几何直观的内涵之一［3］，许多研究也表明，小学生在做作业解决一些数学问题时，画图是一个好办法。

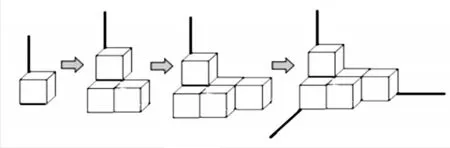
图2

二、经验“禁锢”，致使只见学具操作，学生没有习得想象能力

这里的经验，指教师的教学经验、学习经验、生活经验的综合体，指向于直接感知或领悟到的能够使“好的教学效果”立竿见影的不良经验。经验“禁锢”是指一些教师在通过作业题的设计去引导学生寻找数学联系的过程中，受到自己的不良经验制约，并且在内心适应这种禁锢，拘泥于这种禁锢。其最为明显的特征是机械地割裂“做题”与“意义生成”，忽视重要“联系”。其最为典型的是用正方体拼图中的学具操作问题。也就是，学生在做作业时只是把拼图与学具建立起数学联系，只能借助学具来解决问题。这种误区的表现主要有二：一是安排学生操作学具，甚至提供学具操作过程的示意图，却没有设计让学生想象并推理学具操作过程的提示语与问题。二是绝大多数学生能“正确”解答本道习题，碰到类似习题还需借助学具操作来完成。这样，操作学具就成为了学生正确解题的唯一手段，其目的已不再是帮助学生形成空间想象能力，而是“正确”解题。

例如，作业题：下图（见图3）是由棱长1厘米的绿色正方体木块搭成的。如果表面涂上红色后，其中3个面红色的正方体木块有（ ）个，4个面红色的正方体木块有（ ）个。请先用学具小正方体摆一摆，再填空。

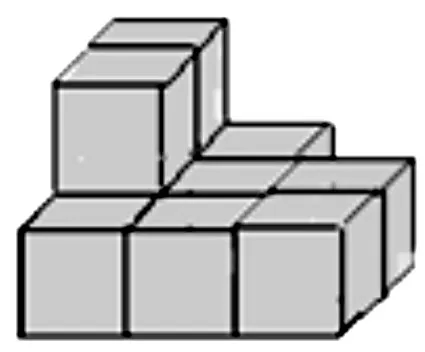
图3

学生对本题进行审题后，会立即按照老师的要求用学具小正方体摆成图3，重点对4 个面红色的正方体木块所在的位置以及其4个红色的面进行观察，然后独立完成填空题。这是典型的教师经验自我“禁锢”致使学生的“习”与“得”割裂的现象。其最直接的负面影响是学具作用被人为夸大，学生只能通过组合正方体来直观解答习题。可以肯定的是，完成这道习题之后，绝大多数学生看着直观图，也无法正确想象出“3 面红”“4 面红”正方体木块所在的位置。也就是，学具操作与空间观念发展没有内在的联结，忽视操作与想象之间的重要“联系”，致使数学思维的跟进滞后，尤其是想象与推理能力的发展没有落实到位。

破解这种误区的对策，简而言之，就是让学具回归本有的地位，把学具的真实操作与想象操作有机结合起来。具体是：首先，在想象与推理的基础上，进行学具操作。设计微视频与提示语，引导学生在操作学具前，通过想象与推理来获得初步结果，并提出解决问题的关键所在。其次，在操作学具的基础上，进行空间位置想象结果的核实与评估。设计微视频与填表题目，让学生通过操作学具来检验初步结果，通过初步反思来完善自己的认识。最后，在总结经验的基础上，进行再想象、再推理。设计微视频与问题串，引导学生再次对学具的操作过程及习题答案的推理过程进行回顾与反思。例如，可以将作业题中原来的提示语改为：请按照以下步骤来摆学具与填空。（1）看着图3想一想：上层有几个小正方体，其中3面红、4面红的小正方体各在哪里，各有几个？下层呢？（2）闭上眼睛，把上述问题再想一遍。（3）睁开眼睛想一想：知道3面红与4 面红的小正方体各自个数的关键是什么？（4）用学具如图3摆一摆，看看你的结论是否正确，并填表（详见表1）。（5）闭上眼睛再次想一想自己解决问题的过程，回答以下问题：3 面红、4 面红小正方体的位置各在哪里，各有几个，为什么？你还能提出什么数学问题？（6）完成作业题中的填空。这样，学生就能够根据直观图来思考，抓住重点位置的正方体木块进行想象与推理。值得注意的是，这道习题中，棱长1厘米的正方体木块总个数是很容易看出来的，但是，它不是3面红木块个数与4面红木块个数之和。

表1

三、现象“迷惑”，致使只盯局部计算，学生没有习得其它方法

本文中的“现象”，指数学作业设计的一种当下状态，是作业与作业设计经历“存在状态”的多样呈现，是数学作业及设计的“图像”。现象“迷惑”是指一些教师自我沉浸于作业设计中的某个数学联系现象，被误导后还津津乐道。其最为典型的是用正方体拼图中的重叠“面”问题。由许多正方体拼成不规则立体图形，一般由两种情况，其一是这些正方体完全相同，其二是这些正方体有大有小。不管是哪一种情况，对于求不规则立体图形的体积来讲，相对于求表面积是容易的。原因何在？这些正方体搭在一起，相邻两个正方体有“面”重叠在一起。换句话讲，求这种不规则立体图形的体积，只要求所有正方体体积的和，而它的表面积则比所有正方体表面积之和少了“许多”。正因为如此，在有关求不规则立体图形表面积的作业设计时，一些教师通过解题思路提示语来引导学生把目光聚焦在相邻两个正方体的重叠部分，就“局部”建立起数学联系，而不从整体上去考虑，不就“整体”建立起数学联系，从而造成误区。

例如，作业题：有四个正方体，棱长分别是2 厘米、2 厘米、4 厘米和6 厘米。把这四个正方体粘合在一起，得到的立体图的表面积最小是（ ）平方厘米。提示：要使得到的立体图形的表面积最小，可以先把棱长6厘米和棱长4厘米的两个正方体粘合在一起，这时，总表面积减少了2 个边长（ ）厘米正方形的面积；再把一个棱长2 厘米的正方体粘上，使它与棱长6 厘米、4 厘米的正方体都有重叠的面，这时，总表面积又减少了4个边长（ ）厘米正方形的面积；最后，把剩下的一个正方体粘上，使它与其余三个正方体都有重叠的面，这时，总表面积再次减少了6 个边长（ ）厘米正方形的面积。

这样设计，看起来引导学生一层一层地深入思考，很是有效。也就是，首先考虑棱长4 厘米的正方体有1 个面与棱长6 厘米的正方体重叠，然后考虑棱长2厘米的正方体有2个面与棱长4厘米、棱长6厘米的两个正方体分别重叠，最后考虑剩下的棱长2厘米的正方体有3个面与其他正方体分别重叠，从而形成下图（见图4）。问题是，仅仅从局部变化去思考，太琐碎，计算不方便，更不利于学生联系自己的长方体表面积计算经验从整体上去解决这类问题。

图4

破解这种误区的对策是“双管齐下”，既从局部去思考，也从整体去架构。本题的“局部思考”作业提示语的设计，上文已经讲过，下面讲如何从整体上去考虑。可以先设计如下提示语：按照题意，把题中四个正方体粘合在一起，得到的表面积最小的立体图形可以见图4。要使得到的立体图的表面积最小，应该使它的三视图面积之和最小。如图4，从上面看，应是边长（）厘米的正方形；从侧面看，应是边长（）厘米、（）厘米两个正方形；从正面看，应是边长（）厘米、（）厘米、（）厘米三个正方形。求这个不规则立体图形的表面积，只要求出三视图的面积和，再乘（）。然后设计如下3 个思考题：这两种解题思路哪一种与长方体的表面积求法完全一致？你更喜欢哪一种？为什么？需要引起注意的是，一般的“迷惑”是解决数学问题的障碍，它本身不能指向问题的解决，而这里的“局部”联系也能解决问题。因此，教师在作业设计中要引导学生加强“双管”的比较，增强学生用这两种方法解这类习题的能力。不仅仅要关注“算法多样化”与“算法优化”，更要关注数感对空间观念的促进作用，关注学生在算法迁移、归纳、优化过程中的思维发展。

综上所述，厘清拼图作业中数学联系的有效性与合理性是数学作业设计的内在要求，明晰拼图作业中数学联系的形式与主体是数学作业设计的重要前提，认清拼图作业中数学联系的设计误区是提高作业设计质量的关键。一些教师由于受习得性思维的束缚，形成了作业设计的误区，制约着学生建立正确的多样的数学联系，需要采取有切实可行的措施来破解误区。