数形结合 直观解题

⦿广东省开平市第一中学

林庆伦

1 引言

数学思想方法相比较于数学基础知识，具有更高的内涵层次和观念性的地位.而数形结合思想，有效实现代数问题与几何问题的等价转化，借助几何直观的分析与代数抽象的探索，寻找更为简单快捷破解问题的方法，从而使得问题得以巧妙破解.

2 破解涉及方程的解或函数零点的问题

在破解涉及方程的解或函数零点的问题时，往往借助两个基本初等函数的构造，结合函数的图象，探讨两函数的交点问题，数形结合，可以直观快捷地处理此类问题.

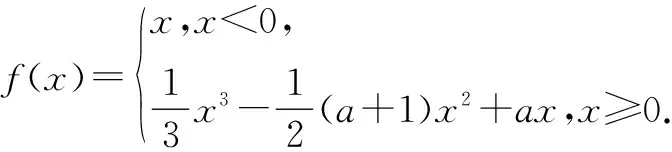
若函数y=f(x)-ax-b恰有三个零点，则( ).

A.a<-1，b<0 B.a<-1，b>0

C.a>-1，b<0 D.a>-1，b>0

分析：利用函数y=f(x)-ax-b恰有三个零点的条件，结合分段函数中自变量的分类讨论，在不同背景下确定零点情况，进而分离参数，根据函数图象，直观剖析参数的取值范围.

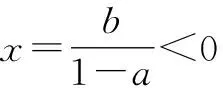
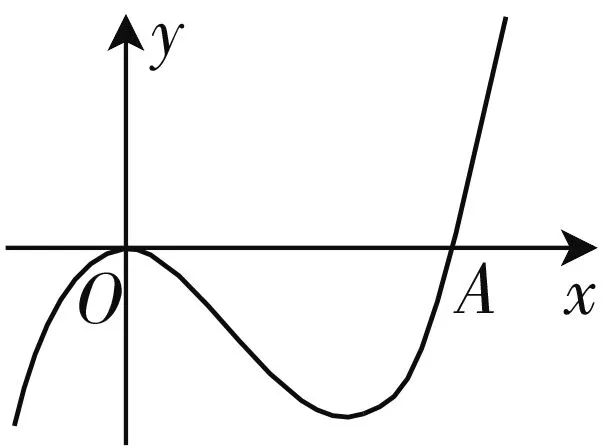
图1

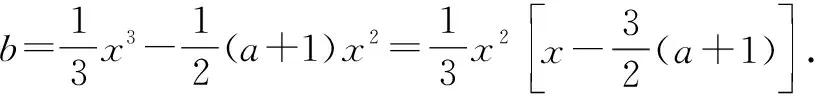
故选:C.

点评：利用数形结合思想破解方程的解或函数的零点问题时，借助函数的图象数形结合，同时一定要注意函数图象的准确性、全面性，否则会得到错解.

3 破解涉及取值范围或最值问题

在破解涉及取值范围或最值问题时，关键是分析题目中相应关系式(等式或代数式)的结构，挖掘其中蕴含的几何特征或几何意义，数形结合.借助几何特征或几何意义的变化情况，直观分析，利用几何法求解.

分析：利用曲线上动点的“动”态，结合两平行线间距离的“静”态及平行直线的设置，数形结合处理.联立方程组，利用方程的判别式加以转化，以代数运算来解决“动”态几何问题，直观有效.

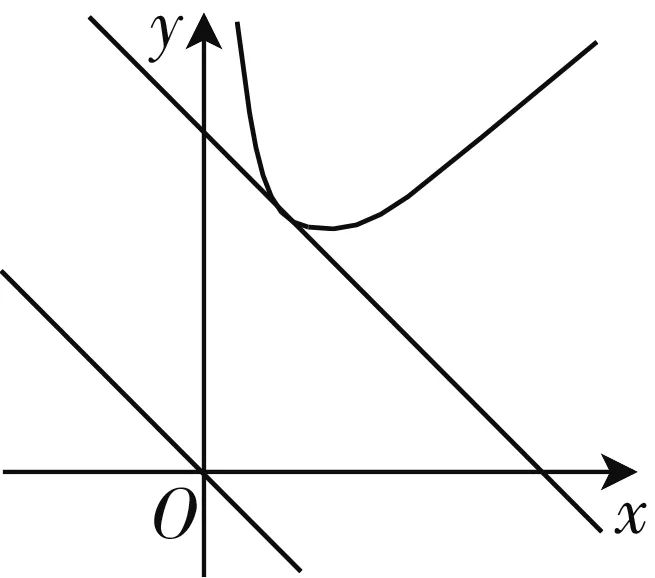
图2

2x2+mx+4=0，

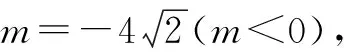
故填答案：4.

点评：在解决一些涉及“动”态的取值范围或最值问题时，通过数形结合，利用对应的几何特征或几何意义的巧妙转化，以及图象的直观想象，对于解决一些参数的取值范围或最值问题有奇效.

4 破解涉及不等式问题

在破解涉及不等式问题时，根据不等式的合理恒等变形，转化为两个熟知的基本初等函数值的大小关系问题.通过数形结合，利用函数图象的位置关系加以直观分析，破解相应的不等式问题.

例3(2020年高考数学北京卷第6题)已知函数f(x)=2x-x-1，则不等式f(x)>0的解集是( ).

A.(-1，1) B.(-∞，-1)∪(1，+∞)

C.(0，1) D.(-∞，0)∪(1，+∞)

分析：通过题目条件中的函数，转化为两个熟知的指数函数与一次函数，结合对应函数的图象，数形结合，直观解决有关不等式的解集问题.

图3

解析：如图3，在同一平面直角坐标系中作出函数y=2x与函数y=x+1的图象.

结合图象可知，两函数对应的交点坐标分别为(0，1)，(1，2).

数形结合可知，不等式f(x)>0的解集是

{x|x<0，或x>1}.

即x∈(-∞，0)∪(1，+∞).

故选：D.

点评：利用数形结合思想破解不等式问题时，借助不等式转化为熟知的基本初等函数问题，一般通过两个基本初等函数的图象加以数形结合，直观处理，往往可以避免繁琐的运算，回避复杂的分类讨论等，获得简捷的解答.

5 破解涉及解析几何问题

在破解涉及解析几何问题时，回归解析几何中点、直线、曲线等之间的图形特征与位置关系，数形结合，通过平面几何图形的特征、性质、关系等加以直观想象，从而快捷简单处理解析几何问题.

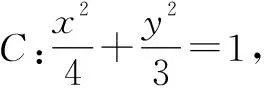
分析：根据题目条件，先确定右焦点F的坐标，数形结合，根据对称点的性质可知x轴平分∠QFQ′，结合垂直确定其角度，得以确定直线的斜率，即可求解对应直线的方程.

图4

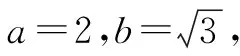
又Q关于x轴对称的点为Q′，且PQ⊥FQ′，如图4所示，根据对称性可知kPF=kl=-1.

所以，直线l的方程为y-0=-1×(x-1)，即x+y-1=0.

故填答案：x+y-1=0.

点评：破解解析几何问题时，经常利用平面几何中点、角、直线、图形等的性质，合理建立相应的关系，直观有效，数形结合破解.

6 总结

合理有效利用数学思想方法破解数学问题，是数学基本内容的深入应用，也是文字和符号的高度抽象与应用，是对数学知识的进一步认识、创新与应用.特别对于数形结合思想的应用，巧妙借助等价性原则、双向性原则、简单性原则等加以分析与处理，直观形象，巧妙破解.