基于自步学习的对称非负矩阵分解算法

王 雷， 杜 亮,2， 周 芃， 吴 鹏,2

(1.山西大学 计算机与信息技术学院 山西 太原 030006；2.山西大学 大数据科学与产业研究院山西 太原 030006；3.安徽大学 计算机科学与技术学院 安徽 合肥 230601)

0 引言

聚类是机器学习常见的任务之一[1-2]，非负矩阵分解(NMF)[3]和K-means[4]都是其重要且经典的算法。但NMF存在一定的局限性：当数据嵌入非线性流形时，NMF不再适用于将其解释为一个原始数据矩阵分解为一个基矩阵与其加权和矩阵。因此，产生了一种NMF的变体——对称非负矩阵分解(SNMF)[5]。一般SNMF的输入为样本间的关系矩阵, 虽然SNMF相对于NMF有了更好的表示能力，但是增加了计算的复杂度。随着对SNMF问题的研究，出现了很多有效的求解算法，例如带有α和β因子的MUR算法[6]；投影梯度下降算法[7]；块坐标下降算法[8]；贪婪梯度下降算法[9]；交替非负最小二乘算法[10]等。但是，SNMF在构造样本的关系矩阵时，会不可避免地出现错误判断的情况。

为解决上述问题，文献[11]引入自步学习框架。自步学习的思想源于课程学习[12]，其核心思想是逐步增加学习的难度来改善模型的训练能力。自步学习有着广泛的应用场景，例如自步矩阵分解[13]；自步聚类集成[14]；基于自步学习正则的无监督特征选择[15]等。本文提出一种基于自步学习的对称非负矩阵分解(SPSNMF)算法，利用自步学习的特性，根据样本损失的大小赋予样本一个可衡量其难易程度的权重变量，以更好地区分正常样本和异常样本，以此来增加模型的稳定性，进而提高聚类任务的准确性。在不同数据集上与多种聚类算法进行对比，实验结果表明了所提算法的有效性。

1 相关工作

1.1 对称非负矩阵分解

对称非负矩阵分解问题是给出一个相似性矩阵X∈Rn×n，其表示一个大小为n×n的对称矩阵，U∈Rn×k为分解得到的低秩矩阵。对称非负矩阵分解的一般问题可以描述为

(1)

其中：U≥0与非对称矩阵分解约束一致。而此时对于模型的求解，从一个二次规划问题转变为一个四次优化问题，复杂度提升。

1.2 自步学习

在聚类任务中，由于数据点的差异性和离群点的存在，在模型训练初期会产生巨大的阻碍，使得模型训练出现偏差，通过加入自步学习框架可以缓解此问题的发生。含有自步学习框架的优化模型可以表示为

(2)

其中：L(θ;xi,yi)为模型的损失函数，θ为决策模型中产生的参数；w=[w1，w2，…，wn]T为用来衡量样本难易程度的权重变量；λ为控制自步函数学习步长的参数。自步函数大体可分为以下两类。

(3)

(4)

2 基于自步学习的对称非负矩阵分解算法

2.1 模型建立

本文模型可以描述为

f(w;λ)，s.t.U≥0,w≥0，

(5)

其中：⊗表示点积；diag(·)表示对角矩阵；w为融入自步学习框架后赋予样本的权重变量，用来衡量每个样本的难易程度；f(w;λ)项用来限定权重，确保模型的合理性。

2.2 模型求解

本文算法的求解采用交替迭代的求解方式。对于U、V的求解采用文献[17]中的求解思路，即采用非对称形式的SNMF模型求解，模型可以描述为

(6)

其中：θ>0为平衡参数。当θ足够大时，式(6)中的任何有界临界点都能满足U=V，并能取到与式(1)中一样的关键点。因此，模型可以重写为

(7)

对于式(7)，U、V、w采取交替更新的方式来进行求解，具体如下。

1)固定w

当更新U和V时，模型可以描述为

(8)

(9)

其中：t表示迭代次数。当固定vi和wi时，式(9)是一个变量为ui的二次方程，对其求导并令其为0，可得ui的更新公式为

(10)

同理，当固定ui和wi时，vi的更新公式为

(11)

因为ui和vi有着非负约束，所以需要给出一个下确界0。

2)更新w

当固定ui和vi时，模型可以描述为

(12)

式(12)是一个变量为wi的凸函数,wi的两种自步函数策略的更新规则分别对应式(3)、(4)。

根据上述描述，本文SPSNMF算法的具体步骤如下。

算法1自步对称非负矩阵分解算法

输入：数据集通过K近邻算法构造相似度矩阵X；聚类数目k。

输出：分解矩阵U。

1: 初始化U0和V0并计算平衡因子θ；迭代次数t=0；

2: 通过计算所有样本的损失函数，选取中位数作为初始自步参数λ的值；

3: while not convergence

4: 通过式(3)、(4)更新w；

5: fori=1:k

7: 通过式(10)更新Ui；

8: 通过式(11)更新Vi；

9: end for

10: 通过式(7)计算目标函数Ft；

12: end while

13: returnU

2.3 模型分析

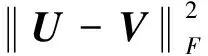
(13)

其中：‖X‖2表示X最大的奇异值；σi(X)表示X的第i个最大奇异值；U0表示U的初始选取值。

2.3.2时间复杂度分析 当更新U时，时间复杂度为Ο(n2k+nk2)，更新V的时间复杂度与U类似。当更新w时，复杂度为Ο(n)。因此，更新所需的时间复杂度为Ο(n2k+nk2)，由于k≪n，故复杂度为Ο(n2k)。假设所有样本全部纳入训练时共进行了P轮(这里的P≪n)，算法在T次迭代后达到收敛条件，故本文算法的复杂度为Ο(TPn2k)。

3 实验与结果分析

对本文所提出的硬加权的自步学习框架(HSPSNMF)和软加权的自步学习框架(SSPSNMF)进行性能评估，将实验参数进行如下设置：平衡因子θ通过式(13)计算，并向上取整；λ的第1次选取为[0.5，1]，随后每次增加10%的样本；设置自步权重在每迭代10次时更新1次，直至所有的样本被纳入训练。为了对比实验的公平性，对每个数据集进行10次实验，取平均值。

3.1 对比方法和数据集

为了衡量本文SPSNMF算法的性能，将其与其他几种密切相关的NMF方法和经典聚类方法进行对比分析。对比方法包括NMF[3]；Ncut[18]；α-SNMF[6]；CIMNMF[19]；L2,1NMF[20]；SPLNMF[21]；SymHALS[17]；CauchyNMF[22]。在对比实验中，将Ncut算法的参数设置为δ∈[2-3，23]，k∈[5，10，15]；将α-SNMF算法的α设置为0.99；CauchyNMF算法采用Nesterov最优梯度法和原始数据自适应加权。数据集的描述如表1所示。

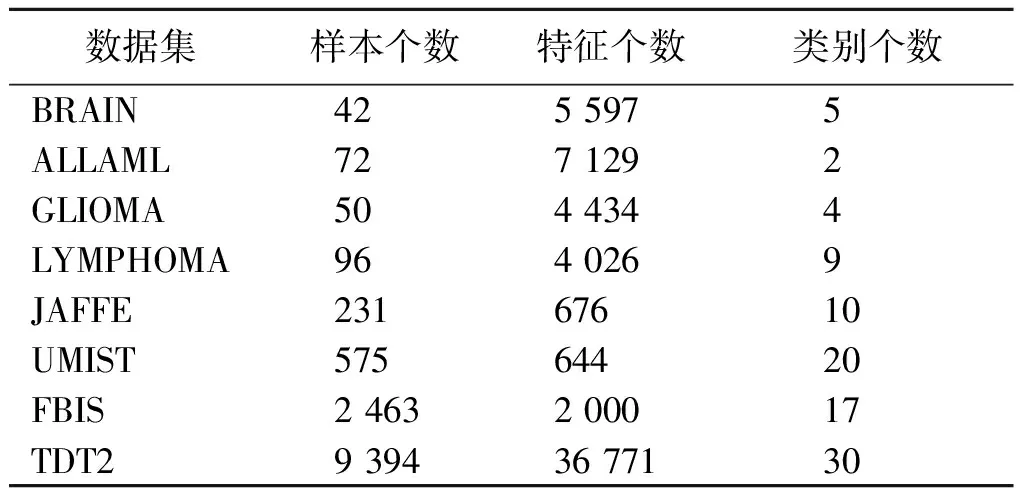
表1 数据集的描述

3.2 收敛性与参数灵敏度分析

以JAFFE数据集为例，将本文HSPSNMF算法与SymHALS算法进行聚类质量和收敛情况对比分析，结果如图1和图2所示。本文HSPSNMF和SSPSNMF算法在JAFFE数据集上添加不同比例样本对聚类精度的影响如图3和图4所示。

图1 HSPSNMF和SymHALS算法在JAFFE数据集上的聚类质量情况

图2 HSPSNMF和SymHALS算法在JAFFE数据集上的目标函数收敛情况

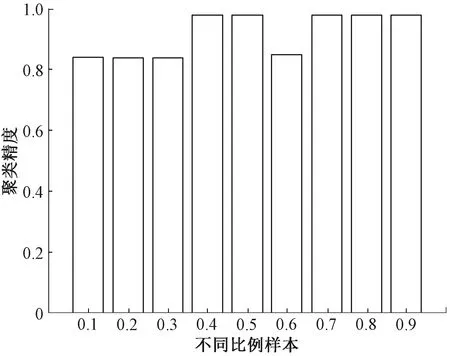
图3 HSPSNMF算法在JAFFE数据集上添加不同比例样本对聚类精度的影响

图4 SSPSNMF算法在JAFFE数据集上添加不同比例样本对聚类精度的影响

图1和图2显示，与SymHALS算法对比，HSPSNMF算法在迭代20次左右即可达到收敛。图3和图4显示，SPSNMF算法中的超参数在初始选取样本比例大于0.4时效果更好。

3.3 评价指标及实验结果

采用的聚类评价指标为聚类精度(ACC)、归一化互信息(NMI)、调兰德指数(ARI)，聚类性能结果分别汇总于表2～4。可以看出，本文方法适用于多个数据集，并且在聚类性能上优于对比算法。

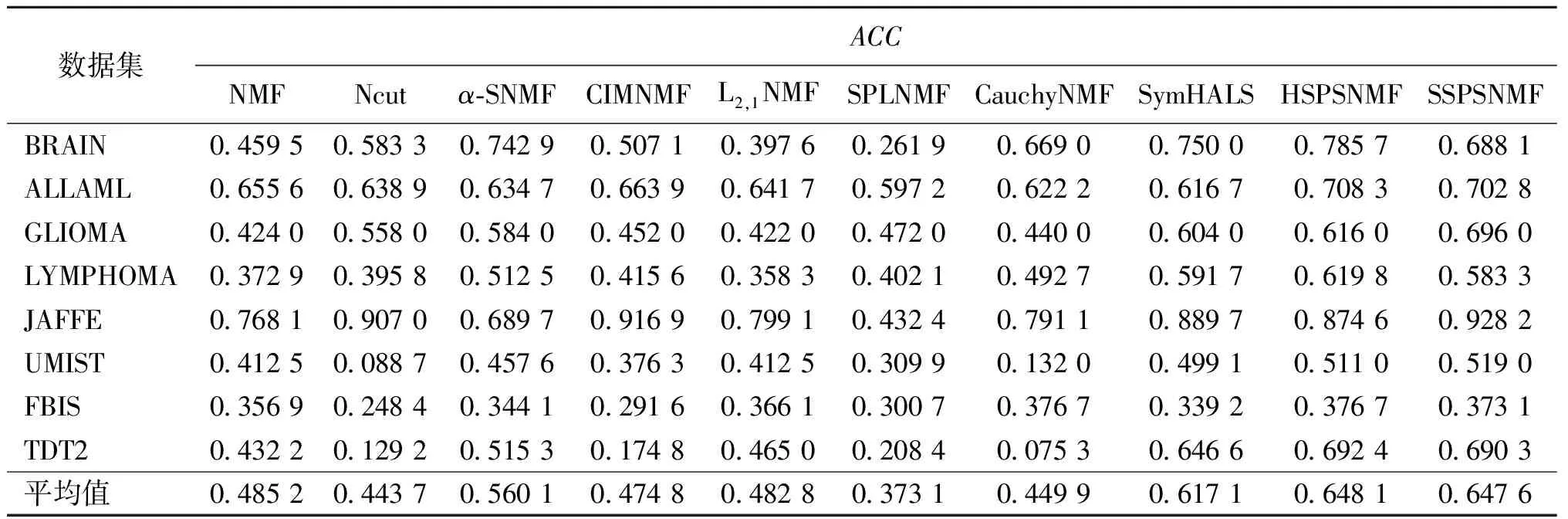
表2 ACC实验结果对比

表3 NMI实验结果对比

表4 ARI实验结果对比

4 小结

本文提出一种基于自步学习的对称非负矩阵分解(SPSNMF)算法，探索了SNMF在加入自步学习框架以后，对其聚类性能的改变以及收敛性。SPSNMF算法具有由简入难地逐步加入样本学习到模型的特性，在很大程度上改善了模型的稳定性和SNMF中相似性矩阵构造时出现错误判断的情况，在聚类性能上相较于其他方法更加稳定。但本文提出的SPSNMF算法存在以下缺陷：在加入自步学习框架后，模型的迭代求解次数增加，进而大大增加了模型的求解时间；对于自步学习中的两种加权策略，未挖掘出其在理论上的可行性以及在不同场景中的适用性。在未来的工作中将进一步探索更高效的SPSNMF求解算法，以及算法在不同类型数据集(例如平衡与非平衡数据)中的应用。