基于Q学习的智能交通信号灯优化

宋国治， 苏鹏博， 刘 畅， 陈玉格

(天津工业大学 计算机科学与技术学院 天津 300387)

0 引言

近年来，随着城市化进程的加快，交通拥堵问题日益严重。交通拥堵所带来的负面影响包括资源的浪费、大气和噪声污染、恶性交通事故的增加等。通过实现自适应交通信号控制智能体可以有效地解决交通拥堵问题，为城市带来经济、环境以及社会效益。十字路口作为提高通行效率的关键位置，理应受到重点关注。目前，许多针对十字路口通行效率的研究都将重点放在优化交通信号灯上。大多数城市的交通信号灯仍然为最传统的定时定序交通信号灯，但其在车流量较大时并不能很好地处理交通流，从而缓解交通拥堵。学者们提出了一些自适应的交通信号灯优化算法，可以根据道路交通的状态来改变信号灯状态，从而实时地对交通流进行调控，但在很多情况下这些算法的收敛速度是有问题的。

随着计算机设备性能的提升，研究人员开始探索使用机器学习等人工智能技术来对信号灯进行优化。目前，使用深度强化学习算法实现自适应交通信号控制是国内外研究的主流方向，出现了一些以DQN(deep Q-network)为研究方向的成果。文献[1]在DQN交通信号控制模型中使用离散交通状态编码(discrete traffic state encoding, DTSE)，将交叉口环境信息用车辆的位置-速度二维矩阵图表示，然后将状态矩阵经过卷积网络提取特征值以获取更有用的信息。文献[2]基于相位切换动作策略实现了一个简单的单交叉口处的信号控制智能体。文献[3]使用自上而下的图像作为DQN的输入，采取DDQN(double deep Q-network)、优先经验池复用、阴影目标网络的集成学习方法，通过训练两个相邻交叉口的交互作用，然后分享学习到的联合Q函数以达到整体最优实现，与DQN相比，DDQN的性能更优。文献[4-5]采取D3QN(dueling double deep Q-network)和优先经验池复用的集成学习方法，在较复杂的单交叉口处实现了一个基于MDP动作空间的自适应交通信号控制智能体，显示出比以往更优的控制效果。本文在上述研究的基础上，提出一种新的交通信号灯优化方法，采用DTSE方式，将车辆的位置-速度二维矩阵图经过卷积网络进行特征提取，以更精确、完整地表示交叉口处实时的环境状态信息，结果表明，基于相位切换和MDP两种动作策略的D3QN交通信号控制模型表现出优秀的信号灯优化效果。

1 Q学习相关算法及其应用

Q学习方法是无模型基于值的强化学习算法[6]，传统的Q学习用表格的方式来记录状态和动作对应的Q值，称为表格型Q学习，适用于解决小规模和离散的状态空间问题。为了使Q学习能解决大规模和连续的状态空间问题，考虑以函数逼近的方法替代表格记录。随着深度神经网络的发展，Mnih等[7]提出一种新的算法DQN，将Q学习与深度神经网络相结合，深度神经网络可以为Q学习提供具有低渐近逼近误差的函数逼近，建立状态到Q值的映射关系。DQN最著名的应用是Deep Mind在2016年推出的AlphaGo围棋系统[8]，使用蒙特卡罗搜索树与深度强化学习相结合的方法，使计算机的围棋水平达到甚至超过了顶尖职业棋手。

因为DQN中动作选取模块和评估模块在同一个网络中，所以会造成过估计的问题。Hado等[9]证明了这种过估计会导致负面的学习效果，并提出将DQL(double Q-learning)[10]与DQN结合，得到一个新的算法DDQN，以解决DQN过估计的问题。DQL防止Q学习产生过估计的基本思想是将选取与评估分开，利用DQN本来就有两个神经网络的天然优势，使用主网络来评估预测值，使用目标网络来估算目标值，有效解决了DQN在学习过程中存在的过估计问题。文献[11]提出dueling DQN,进一步提高了DQN算法的性能。

DQN采用经验池回放算法随机抽取部分经验对主网络的参数进行更新，以消除数据之间的相关性所带来的不良影响。由于经验的采样是随机的，每条经验被挑选的概率相同，不能体现经验之间重要性的不同，而一些更重要的经验应当被优先调用，因此发展出了优先经验池复用[12]，为每条经验赋予优先级以区别不同经验的重要性。D3QN算法结合了上述算法的优点，能以更好的性能进行数据的处理，在信号灯优化上表现出优秀的性能。

2 基于D3QN的交通信号控制模型

2.1 深度强化学习在交通信号控制中的应用

在深度强化学习的交通信号控制方法中，智能体在闭环系统中与环境不断进行交互，根据实时的交通状态获取状态信息，在动作空间中选取动作对环境做出响应，观测该动作所造成的结果给予奖励值，并根据结果来调整自身动作选择机制，最终让智能体可以对外界环境达到最优响应，以获得最大的累计奖励值为目标，从而学习到对自身动作的最优控制方法。

2.2 深度强化学习中的三个重要因素

1)状态空间

DTSE[1]将环境的状态信息用多维表示，一般由三个维度构成：第一维表示区间内是否有车辆；第二维是车辆的速度；第三维是信号灯的时间相位。对于交叉口处每一条驶入车道(驶向红绿灯)，DTSE规定从车道停止线开始往后的固定长度L内，将其按间隔距离c划分为若干个等距区间。DTSE离散矩阵如图1所示。本文采用位置-速度二维矩阵图来表示环境的状态信息，第一维的布尔值0或1表示车辆是否存在，第二维的整数值表示车辆的取整速度，然后再将这个矩阵图输入到卷积网络进行特征提取，得到更精确、完整的状态信息。

图1 DTSE离散矩阵

2)回报函数

在时间步为t时，回报函数rt=wt-1-wt，其中：wt为t时刻所有驶入车道上的车辆的总等待时间；wt-1为t-1时刻所有驶入车道上的车辆的总等待时间。回报值就是当前驶入车道上的车辆的总等待时间减去上一步的车辆的总等待时间。

3)动作策略

策略1(相位切换)。在这个策略中，智能体需要选择下一步是保持当前的绿灯相位或是切换到另一个指定的绿灯相位，当切换相位时，需要设置上一个绿灯相位变为黄灯，再切换到选择的绿灯相位。由于相位切换策略是在相位间进行随意切换，因此在一定程度上会使系统变得不太稳定。

策略2(MDP动作空间)。在这个策略中，动作空间被定义为选择下一个循环中各个绿灯相位的持续时间。在一个循环中绿灯相位的切换顺序固定，这样就避免了相位切换策略中为保持当前相位而造成的规避黄灯时间。每轮完一遍为一个循环，为了避免两个循环之间相位时间差异过大而给系统造成不稳定，相邻循环间相位持续时间应平滑地改变，因此将动作空间建立为一个高维的MDP模型。以图1的交叉口处场景为例来说明MDP动作空间。信号灯有四组绿灯相位：相位1，南北直行右转；相位2，南北左转；相位3，东西直行右转；相位4，东西左转。每个循环的相位顺序为〈phase1,phase2,phase3,phase4〉，对应的持续时间为〈t1,t2,t3,t4〉,t∈[5,60]，智能体在每一步(一个循环结束时)需要选择下个循环中的一个相位，决定其增加或减少5 s，或保持不变。

2.3 D3QN模型的算法介绍

本文使用的D3QN模型是在DQN的基础上添加了double DQN与dueling DQN构成的。本文模型通过卷积神经网络来获取当前道路中的特征信息，使用double DQN来解决过估计问题，并使用dueling DQN来加快收敛速度。此外，通过优先经验池回放与ε-greedy策略来提高算法的性能。

1)卷积网络

D3QN模型架构如图2所示，由三层卷积层和两层全连接层构成，模型的输入大小为50×50×2，对应的交叉口划分为50×50个等大的区间，在每个区间上将包含车辆位置-速度信息的二维矩阵图作为输入，经过三层卷积网络进行特征提取，获取更精确的状态信息。

图2 D3QN模型架构

卷积网络由卷积层、池化层和ReLU层构成。卷积层包含多个具有不同权重的卷积核，通过卷积层获得一张抽象的特征图。池化层选取每个区块上最显著的元素来替代区块，可以有效减少图像的大小。ReLU层使用线性整流f(x)=max(0,x)作为激励函数，可以增强判定函数和整个神经网络的非线性特性，提高神经网络的训练速度。本模型中三层卷积网络的参数设置如表1所示。

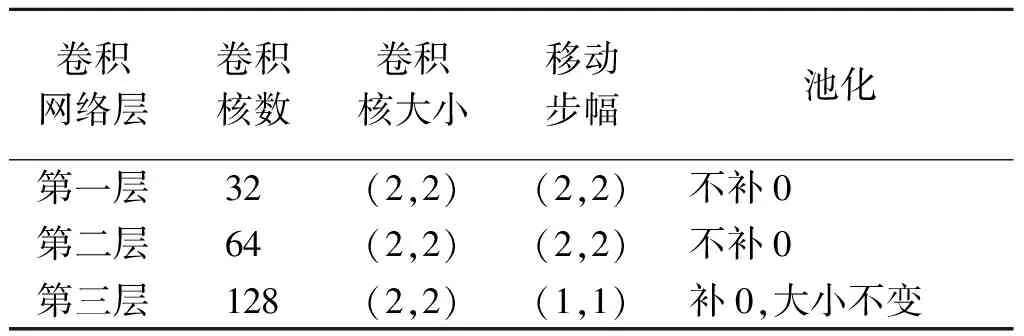
表1 三层卷积网络的参数

2)目标网络

传统的表格型Q学习不适用于大规模和连续的状态空间，更好的办法是找到某一参数θ来近似Q函数，以函数逼近的方式取代表格记录，即

Q(s,a;θ)≈Q(s,a)。

(1)

Q学习中Q值的更新需要每次Q值的预测值及目标值，目标值使用下一个状态Q值的预测值来近似。更新表达式为

Q′(s,a)=Q(s,a)+α(r+γmaxQ(s′,a′)-Q(s,a))，

(2)

其中：Q(s,a)为Q值的预测值；r+γmaxQ(s′,a′)为目标值。

为了避免DQN中目标值的频繁变动，建立了两个结构完全相同但参数不同的网络：一个是主网络，参数θ用于输出预测值；另一个是目标网络，参数θ′用于输出目标值，使目标网络以比主网络更低的频率进行更新，以此保证目标值在一段时间内是稳定的。DQN中主网络通过损失函数的引导进行更新，θ的更新应使损失函数最小化。损失函数定义为目标值与预测值的均方差，其表达式为

L(θ)=(r+γmaxQ(s′,a′;θ′)-Q(s,a;θ))2。

(3)

主网络根据损失函数，通过梯度下降法更新参数θ。目标网络的更新表达式为

θ″=αθ′+(1-α)θ，

(4)

其中：α是更新频率速度参数，表示主网络参数θ对目标网络参数θ′的影响程度。目标网络可以使DQN模型保持稳定。本文模型采用目标网络，使用两个结构相同但参数不同的神经网络，根据损失函数L(θ)通过梯度下降法更新主网络，并根据式(4)使目标网络以更低的频率进行更新。

3)double DQN

在DQN中，由于预测值和目标值都由主网络产生，即动作的选取和评估都由主网络决定，因此造成DQN在学习过程中产生过估计问题。DDQN(double DQN)利用DQN中原有的两个网络，令主网络选取最优动作，令目标网络计算目标值，将动作选取模块与评估模块相分离。DDQN中目标值的计算公式为

TDDQN=r+γQ(s′,argmax(Q(s′,a′;θ));θ′)。

(5)

DDQN中Q值的更新表达式为

Q′(s,a;θ)=Q(s,a;θ)+α(r+γQ(s′,

argmax(Q(s′,a′;θ));θ′)-Q(s,a;θ))。

(6)

DDQN可以有效克服DQN模型中存在的过估计问题，提高算法的性能。

4)dueling DQN

DQN输出n个Q值(n代表可选择的动作个数)，而dueling DQN 输出的是两个变量：状态自身价值V和动作效益A。V代表在当前状态s下Q值的平均期望(综合考虑了所有可选动作)；A代表在选择动作a时Q值超出期望值的多少。Q值间接等于V与A的和。V的计算公式为

Vπ(s)=Eα～π(s)[Qπ(s,a)]。

(7)

A的计算公式为

Aπ(s,a)=Qπ(s,a)-Vπ(s)。

(8)

通过V和A来计算Q值的表达式为

Q(s,a;θ)=V(s;θ)+(A(s,a;θ)-

(9)

A可以体现出一个动作在所有动作中对值函数的重要性。从奖励值上看，如果一个动作的A为正数，那么这个动作的性能在所有可能动作的平均性能之上；如果一个动作的A为负数，那么这个动作的性能在所有可能动作的平均性能之下。

5)优先经验池回放

DQN采用经验池回放，在经验池中进行随机采样，以消除因为采样数据之间相互关联所造成的不稳定性。优先经验池回放在经验回放的基础上，给每条经验加上一个优先级以区分不同经验的重要性，使得模型的训练速度更快且性能更优。本模型中优先级的大小由每条经验的时间差分误差值决定，定义为

δi=|Q(s,a)i-Qtarget(s,a)i|=

|Q(s,a)i-r-γQmax(s′,a′)|。

(10)

时间差分误差值越大，代表这条经验越需要优化，优先级越高。

6)ε-greedy策略

D3QN的学习有个探索过程，智能体在探索时期进行动作的随机选取，前期的探索可以让智能体积累更多的经验。但是，随着学习的推移，D3QN网络趋于收敛，预测出的Q值越来越准确，此时智能体应该减少探索量，更多地选取最大Q值对应的动作去执行，这个动作选取过程被称为利用。ε-greedy策略的作用就是控制D3QN模型在整个学习过程中探索与利用的比重，设置探索概率ε，ε随着迭代次数而衰减，其表达式为

ε=εmin+(ε-εmin)e-λn，

(11)

其中：εmin为最小探索概率；λ为衰减率(0<λ<1)；n为迭代次数。

7)D3QN整体算法

首先对模型的各项参数进行初始化，然后从仿真软件获取状态信息传入卷积神经网络，由神经网络输出预测的动作Q值组，再由ε-greedy策略判断是随机选取动作还是选择动作Q值组中对应最大Q值的动作。仿真软件执行动作后，获取下一个时间步的状态和奖励值，将当前状态s、动作a、回报值r、下一步状态s′组成的四元组〈s,a,r,s′〉存入经验池中。通过优先级排序从经验池中随机抽出一部分经验，用于更新主神经网络的参数，再以较低的频率更新目标网络的参数，重复这个过程进行训练。

3 实验结果与分析

3.1 交通仿真环境

本实验使用SUMO交通仿真软件，利用SUMO提供的Python APIs接口，通过Traci模块获取实时交通环境状态信息，并对信号灯进行动作控制。

实验模拟了一个大小为300 m×300 m的交叉口，如图3所示，交叉口由四条相互垂直的道路组成。每条道路有三个车道：一个车道允许右转和直行，一个车道只允许直行，剩下一个车道只允许左转。绿灯持续时间初始均为20 s，黄灯持续时间为4 s。

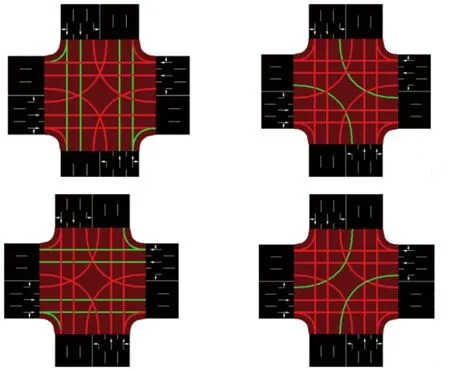
图3 SUMO交叉口模型

车流文件通过随机函数生成，包含车辆的出发时间、出发点以及行驶方向。具体的车辆信息为长度5 m，最小间隔距离2.5 m，出发速度10 m/s，最大速度13.9 m/s，最大加速度1 m/s2，最大减速度4.5 m/s2。模型采用两种迭代训练的方式：第一种是针对同一个车流文件进行重复的迭代训练；第二种是设置随机数种子，将车流文件与迭代回合数关联，每个回合对应固定的车流文件，各个回合的车流文件不相同，以实现训练的重现。

3.2 模型的训练参数

D3QN模型中各个参数的设置相同。经验池大小为20 000，批处理大小为64，初始探索概率为1，最小探索概率为0.01，探索概率衰减率为0.000 1，折扣系数为0.99，学习率为0.000 1，目标网络更新率为0.001。

3.3 传统的定时定序红绿灯控制策略

为了将本文模型与传统的红绿灯控制策略进行对比分析，实现了一个传统的定时定序红绿灯轮转策略，车辆的平均等待时间变化曲线如图4所示。可以看出，传统的红绿灯控制策略在相同的交通环境中车辆的平均等待时间在(46±5)s范围内浮动。

图4 传统的红绿灯控制策略下车辆的平均等待时间变化曲线

3.4 相位切换策略

相位切换策略下累计奖励值变化曲线如图5所示。可以看出，在100轮之前累计奖励值快速增长，接着趋于稳定，在后期略有下降。相位切换策略下车辆的平均等待时间变化曲线如图6所示。可以看出，在训练后期，车辆的平均等待时间稳定在25 s以下，但是有微小的上升趋势。

图5 相位切换策略下累计奖励值变化曲线

图6 相位切换策略下车辆的平均等待时间变化曲线

此外，在训练过程中，相位切换策略下车辆通过数变化曲线如图7所示。可以看出，只有第一轮中车辆的通过数为3 499辆，后续回合中所有车辆(3 500辆)均能通过交叉口。

图7 相位切换策略下车辆通过数变化曲线

对比发现，传统的红绿灯控制策略下车辆的平均等待时间(图4)在46 s上下小幅度浮动，而相位切换策略下车辆的平均等待时间在训练后期稳定在25 s以下，相比传统的红绿灯控制策略减少了约45%，且相位切换策略在训练过程中可以保持稳定的性能，车流量除第一轮为3 499辆外一直维持在3 500辆。

3.5 MDP动作策略

MDP动作策略下累计奖励值变化曲线如图8所示。可以看出，随着训练的进行，累计奖励值稳定增长，在200回合后趋于收敛。

图8 MDP动作策略下累计奖励值变化曲线

MDP动作策略下车辆的平均等待时间变化曲线如图9所示。可以看出，在训练过程中，车辆的平均等待时间呈下降趋势，随着训练回合数的增多下降幅度逐渐平缓，维持在10 s上下小幅度浮动，与初期相比，平均等待时间减少了75%。

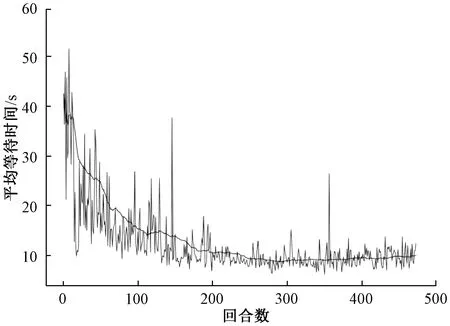
图9 MDP动作策略下车辆的平均等待时间变化曲线

在训练过程中，MDP动作策略下车辆通过数变化曲线如图10所示。可以看出，在第100～200回合，MDP动作策略并不能使3 500辆车全部通过交叉口，但是随着训练的进行，通过的车辆数稳定增长，在200回合后可以基本保持使全部车辆通过交叉口。

图10 MDP动作策略下车辆通过数变化曲线

分析发现，经过200回合的训练后，MDP动作策略下车辆平均等待时间在10 s上下小幅度浮动。与传统的红绿灯控制策略的车辆平均等待时间相比，减少了约78%；与相位切换策略的车辆平均等待时间相比，减少了约40%。因此，从最终结果来看，相比相位切换策略，MDP动作策略对于交叉口处车辆等待时间的优化效果更佳。

相位切换策略在整个训练过程中能基本保持所有车辆在固定步数内通过，而MDP动作策略在第100～200回合的车流量却一度下降到3 000辆以下，最差时仅有约2 200辆车通过交叉口，车流量减少的错误会随着学习回合数的增多而逐渐被优化。在前中期的学习过程中，相位切换策略要比MDP动作策略更稳定。导致此现象主要是由于MDP动作空间的大小为9，而相位切换策略动作空间的大小仅为4，因此MDP动作策略的计算量要比相位切换策略大，收敛速度会更慢些。

4 小结

本文利用基于两种动作策略的D3QN交通信号控制模型在SUMO交通仿真软件上进行了模拟训练，与传统的红绿灯控制策略进行对比发现，相位切换策略下车辆平均等待时间减少了约45%，而MDP动作策略下则减少了约78%。可见，MDP动作策略训练的最终结果要优于相位切换策略，但是MDP动作策略因动作空间稍大，计算量要比相位切换策略大，收敛速度会更慢些，在训练前中期的表现不太稳定。