程序求精新策略及自动验证方法研究

左正康， 黄志鹏， 黄 箐， 王 渊， 王昌晶

(1.江西师范大学 计算机信息工程学院 江西 南昌 330022；2.江西师范大学 软件学院 江西 南昌 330022)

0 引言

随着计算机软件的日益发展，软件的可靠性在各个领域中受到高度重视，而算法程序的正确与否是软件可靠性的关键，尤其在安全攸关的系统中，算法程序错误往往会导致巨大的损失和社会影响[1]。传统的设计与描述方法难以保证算法程序的正确性，而形式化方法[2]是保证程序正确性的根本途径。程序求精是自动推理和形式化方法相结合的技术，能提高算法程序开发的效率和正确性[3]。抽象的形式规约经过一系列的求精变换步骤，最终得到计算机能执行的程序代码[4]。算法程序的生成以及正确性可以通过精化规则来保证，将程序开发与程序验证交替进行，也可以在事后采用验证工具来证明。我国建立了以形式化方法正确构造程序、覆盖软件全周期、以可信要素为核心的航天嵌入式软件可信保障技术体系，并运用于“嫦娥”等重大工程中，软件的可信性得到了重要保障[5]。程序求精策略及自动验证方法的研究对提高软件开发的效率和正确性有一定意义。

从问题规约出发，使用各种规则进行演绎推理，文献[6-7]提出并发展了一种基于演绎推理的程序开发方法，使程序开发和正确性验证同时进行，但其无法求精至可执行程序。文献[8-9]基于PAR方法[10]对多类算法进行程序求精，扩展了PAR方法的应用范围，进一步简化了多类算法的推导和证明，但其生成的Apla抽象程序经人工推导而成，后续并未进行机器辅助证明，验证的可信度较低。文献[11-12]使用Isabelle定理证明器[13]对形式化推导生成的抽象程序进行机械验证，但其验证条件是手工生成的，自动化程度不足。本文针对以Morgan[14]为代表的传统程序求精方法无法求精至可执行程序的问题，利用平台生成可执行程序，提高了程序求精的完整度；利用VCG可自动生成验证程序正确性的条件，大幅度提高了算法程序验证的自动化程度；使用Isabelle定理证明器辅助证明求精得到的IMP程序[15]，确保了验证的可信度。

1 程序求精及自动验证策略

针对传统的程序求精所存在的问题，提出一种新的求精策略及自动验证方法，如图1所示。

图1 程序求精及自动验证策略

1.1 初始规约生成

本策略借助形式化方法来描述问题，首先生成该问题的初始规约(P,Q)，其中P和Q分别为该算法程序的前置条件和后置条件。P为程序执行之前满足的条件，其规约较容易获得；Q表示程序终止时应满足的条件，可用一阶谓词逻辑来形式化描述。一阶谓词逻辑是采用统一形式(θi:r(i):f(i))来表示的,其中：i为量词θ的约束变量；r(i)为逻辑表达式，表示i的变化范围；f(i)为一个函数或表达式。

1.2 形式规约IMP

1)初始规约变换

规约表示方式的不同具体表现在实现其功能的数据结构和算法上。对于生成的初始规约，用一阶谓词逻辑表示后置条件。随着问题复杂度的增加，使用一阶谓词逻辑形式化表示往往显得冗长，且容易出错。本策略使用递归定义函数技术对初始规约进行变换，进一步扩充Morgan精化方法，有利于寻找递推关系和进行算法程序推导，并且递归基于严格的数学逻辑，更容易保证推导过程的正确性，对Isabelle的自动验证也提供了便利。

利用递归定义函数技术对初始规约中的后置条件(θi:r(i):f(i))进行变换，生成与初始规约(P,Q)等价的s:[P,Q]框架，其中s为满足规约P到规约Q求精过程中的框架变量。初始规约变换过程如图2所示。

图2 初始规约变换过程

2)Morgan精化规则

程序求精的过程中要注意保证程序的正确性，即保证所得到的程序是满足初始规约的，那么程序的正确性可以通过求精过程中所遵循的一系列规则来保证。本文的求精策略基于Morgan精化规则，规约通过求精规则完成精化，使用定理证明器辅助验证得到的IMP程序。

1.3 IMP自动验证

1)验证条件生成器(VCG)

VCG可以自动生成验证程序正确性的条件，再由定理证明器进行证明，从而大大提高了算法程序验证的自动化程度。VCG实现了霍尔逻辑规则的自动化和形式化，在Isabelle定理证明器中利用VCG验证算法程序，需要提供该算法的初始条件、前后置断言、循环体和循环不变式[16]，VCG代码结构如图3所示。VCG基于pre和vc两个函数，pre函数类似于Dijkstra最弱前置谓词方法，vc函数的作用则是生成验证条件。

图3 VCG代码结构

2)Isabelle定理证明器

传统的手工验证可信度不高，而机械化定理证明器以数理逻辑和类型论的研究成果为基础，其证明的可靠性远胜于手工验证[17]。Isabelle作为一种通用的定理证明器，支持对数学公式的形式化描述，且为公式的逻辑演算提供了证明工具。

Isabelle定理证明器支持模块化设计，可通过定义新的类型、常量和规则对父理论进行扩充，其系统中的Sledgehammer工具[18]可调用另外的定理证明器来辅助证明，如E、SPASS、Vampire等。利用VCG与Isabelle定理证明器相结合，对IMP程序进行验证，若验证成功，则进入算法程序开发的下一阶段；若验证失败，则人工分析程序求精步骤，对其中的关键步骤进行单步验证，查找失败原因。

1.4 IMP到C++可执行程序

程序求精得到的IMP程序仍然是抽象程序，无法在计算机里编译运行。借助本团队开发的C++程序自动生成系统[19]，将IMP程序转换成C++可执行程序，并将编译工作交付给第三方编译器，从而保证了转换系统的可靠性，实现了从问题描述到正确开发可执行程序的全过程。图4为IMP到C++程序自动生成系统的总体结构。

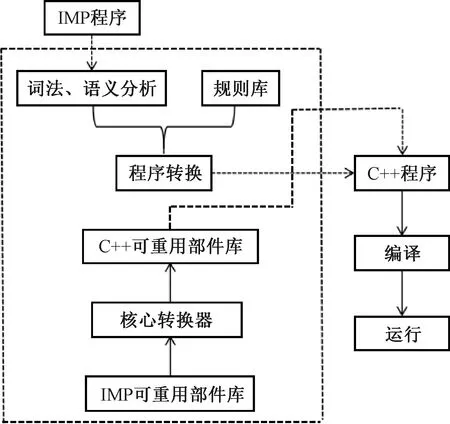
图4 IMP到C++程序自动生成系统的总体结构

2 实例：最长标志基因序列问题

2.1 初始规约生成

问题描述：有一串已知长度的基因序列，如“1010100100001000…”,“0”代表一个标志基因。计算基因序列中标志基因的最长连续长度，将基因序列存放于数组A[0:n]中，其中n=A.len-1，A.len>1，且数组的第一个元素A[0]存放该基因序列的长度值。前置条件表示为P:A.len>1，后置条件用一阶谓词逻辑形式表示，则Q可以表示为

(maxi,j:1≤i≤j≤n∧(∀k:i≤

k≤j:A[k]=0):j-i+1)。

(1)

2.2 程序求精

2.2.1初始规约变换 使用递归定义函数技术对初始规约进行变换，定义递归函数maxj(j,A)，其表示当遍历到节点A[j]时当前的标志基因长度，A[j]存在两种情况，即A[j]=0和A[j]≠0。maxj(j,A)函数的具体说明如图5所示，其中标志基因用“0”表示，非标志基因为空白。

图5 maxj(j,A)函数的具体说明

maxj(j,A)=

maxj(j,A)只记录当前的标志基因长度，因此还需定义函数maxgene(j,A)，其记录基因序列A[0:j]中标志基因的最长连续长度。maxj(j,A)的值与当前A[j]的值有关，不能保存前面标志基因段的长度。maxgene(j,A)函数的具体说明如图6所示。

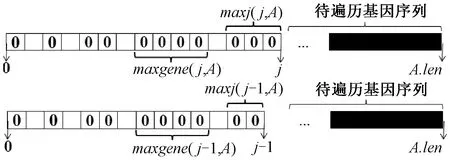
图6 maxgene(j,A)函数的具体说明

maxgene(j,A)=

则(1)式可以表示为

(maxi,j:1≤i≤j≤n∧(∀k:i≤k≤j:

A[k]=0):j-i+1)=maxgene(n,A)。

将生成的前置规约和后置规约进行初始规约变换，形成新的框架，并引入框架变量mg，用来保存基因序列中标志基因的最长连续长度，则有

mg:[A.len>1;mg=maxgene(n,A)]。

(2)

2.2.2开发循环不变式 开发循环不变式如图7所示。选取变量i(0

图7 开发循环不变式

inv≡(mg=maxgene(i-1,A))∧

(mj=maxj(i-1，A))∧i≥1∧i≤A.len。

利用循环不变式与后置断言的关系，添加条件i=A.len，那么问题规约的后置条件可以通过循环不变式来构造，即

(mg=maxgene(n,A))≡(inv∧i=A.len)。

根据文献[12]的强化后置断言规则，原始规约精化为

i,mg,mj:[A.len>1,inv∧i=A.len]。

(3)

2.2.3循环变量初始化 选择inv作为连接前置规约和后置规约的中间断言，根据文献[12]的顺序组合规则，式(3)精化为

i,mg,mj:[A.len>1,inv]；

i,mg,mj:[inv，inv∧i=A.len]。

(4)

对于式(4)的第1部分，根据文献[12]的赋值传递规则，有

因此，上述精化成立。

2.2.4循环过程精化 对于式(4)的第2部分，i=A.len是退出循环的条件，根据文献[12]的循环规则，有

od

C2

其中，V0是V在上一次循环中的值。因为i是从左至右遍历数组的索引，所以可将V定义为A.len-i。设i在上一次循环中的值为i0，将V=A.len-i代入0≤V

接着考虑循环体内部，i是不断递增的，根据文献[12]的赋值传递规则，有

C3

完成对i的精化后，可将约束变量i删去，规约及变换过程更新为

对1≤i+1≤A.len和i0

因为mj的值存在变化，mg始终保存区间(0,i-1]找到的最长标志基因的长度，所以需要取mg和mj的最大值。根据文献[12]的赋值传递规则，对mg进行精化，有

C4

完成对mg的精化后，可将约束变量mg删去，规约及变换过程更新为

mj:[inv∧i≠A.len,(mg=maxgene(i,A)∧

mj=maxj(i,A)∧1≤i+1≤

A.len)[mgmax(mg,mj)]]≡mj:[inv∧i≠A.len,

(max(mg,mj)=maxgene(i,A)∧

mj=maxj(i,A)∧1≤i+1≤A.len)]。

根据文献[12]的选择规则，可得

fi

C5

将语句C1、C2、C3、C4、C5组合，最终生成的IMP程序为

C1

doi≠A.len→

C2

C5

fi

C4

C3

od

2.3 使用VCG的Isabelle自动验证

2.3.1VCG生成验证条件 创建定理maxgene，对生成的IMP程序进行验证。在语句C1前添加前置断言{1

接着使用Isabelle命令apply vcg自动生成程序的3个验证条件，结果如图8所示。

图8 自动生成验证条件

2.3.2Isabelle自动验证 针对3个验证条件，使用Isabelle定理证明器验证其正确性，具体步骤和部分代码如下。

1)定义递归函数maxj和maxgene。

2)创建引理recur1并证明，对定理提供辅助引理：

lemma recur1[simp]: "i ≥ 0⟹(max(maxgene i A)(maxj(Suc i)A))=(maxgene(Suc i)A)"

apply auto

done

3)使用apply命令和Sledgehammer工具对验证条件进行证明，命令如下：

apply simp

apply(smt One_nat_def Suc_le_mono

add.left_neutral add_Suc_right

add_diff_cancel_right

le_add_diff_inverse maxj.simps(2)

nat_minus_add_max recur1 zero_le)

using not_less_eq_eq by force

最终验证成功，结果如图9所示。通过C++程序自动生成系统，可将IMP抽象程序自动生成对应的C++程序。自动生成最长标志基因问题的C++程序如图10所示，左边为最长标志基因序列问题的IMP程序，右边为转换的C++程序。对生成的C++程序进行测试，输入任意一段基因序列，测试结果正确，如图11所示。

图9 IMP程序验证正确

图10 自动生成最长标志基因问题的C++程序

图11 自动生成C++程序的测试结果

3 结束语

本文提出一种新的程序求精策略，以最长标志基因序列问题为实例，从问题描述出发，使用递归定义函数技术对初始规约进行变换，并基于Morgan精化规则对规约进行一系列的求精变换得到IMP程序。使用VCG自动生成验证程序正确性的条件，通过Isabelle定理证明器验证其正确性，在程序正确性得以保证的情况下，开发平台最终生成C++可执行程序，实现了从问题规约到可执行程序的求精全过程，提高了形式化验证的自动化程度和可信度。