含负泊松比超材料肋板的双层板声振特性分析

张兆龙， 朱 翔,2,3， 李天匀,2,3， 付俊勇

(1.华中科技大学 船舶与海洋工程学院，武汉 430074; 2.船舶与海洋水动力湖北省重点实验室，武汉 430074;3.高新船舶与深海开发装备协同创新中心，上海 200240)

负泊松比超材料具有特殊的“拉胀”[1]效应，在受拉时能够在多个方向同时伸展，宏观上体现为负的泊松比值。在航空航天、船舶工业、汽车制造等领域，负泊松比超材料因为力学性能优异而极具研究和应用价值。

目前大多有关负泊松比超材料的研究工作集中于其静态力学性能[2]、冲击力学性能[3]、面内压缩性能[4]等的分析，在单胞设计[5]、制备工艺[6-7]、工程应用[8-9]等方面取得诸多成果。在力学性能方面，Lu等[10]发现在内六角蜂窝构型晶胞中添加肋条会显著提升杨氏模量，结构整体的机械性能得到明显改善。Chen等[11]提出了3种新型负泊松比单胞，该类单胞能够同时具有较好的承载能力和吸能特性。在胞元设计方面，Qin等[12]将拓扑优化技术应用于负泊松比单胞的设计，将评价点的位移比近似为等效负泊松比，提出了一种设计任意负泊松比单胞的通用方法。在声振研究方面，Ruzzene等[13]研究了六边形胞元夹层梁的振动和声辐射特性，对比分析了不同夹层型式梁的结构响应差异和声压分布。Idczak等[14]分析了拉胀材料晶格结构的动力学特性，研究了该类材料的频响特性。总体而言，已有的负泊松比超材料研究中，关注其振动声学特性并将其应用于结构减振设计的工作还相对欠缺。

双层板结构是工程中广泛使用的结构类型，对其开展振动噪声控制研究具有重要意义。本文将含内六角负泊松比胞元的结构用于双层板的连接肋板中，分析其振动特性，并与常规平板连接的双层板结构进行对比，讨论负泊松比层间结构的参数对声振特性的影响，这对于将负泊松比超材料应用于工程中声振控制具有参考意义。

1 内六角蜂窝胞元几何特征与力学性能

本文分析的内六角蜂窝单胞的几何构型，如图1所示。由参数底边长度h、斜腰长度l、特征凹角θ、胞元厚度t确定。单胞的泊松比特性与特征凹角θ有关，以图示为例，定义沿竖直线逆时针方向角度为正，则当θ<0°时，胞元才具备负泊松比特性，当θ>0°时，胞元变为凸六边形，泊松比恢复为正值。

图1 内六角蜂窝单胞几何参数

Gibson等依据线弹性理论，推导了内六角蜂窝单胞的等效泊松比解析式如式(1)，该理论忽略了t/l这一小量，且不考虑轴向变形和剪切变形，仅关注起主要作用的弯曲变形。

(1)

等效杨氏模量、等效剪切模量、相对密度的计算式分别为

(2)

(3)

(4)

式中：Es为胞元本体构造材料的杨氏模量；ρ*为不考虑孔隙的材料真实密度；ρs为单胞围壁面密度。

2 含负泊松比超材料肋板的双层板声振特性

2.1 含负泊松比超材料肋板的双层板模型

本文设计的双层板尺寸为长1 500 mm、宽1 030 mm、上、下面板的间距150 mm。连接上、下面板间的肋板间距为500 mm，肋板宽度为20 mm，负泊松比胞元层数为5层。负泊松比肋板示意图、内六角单胞尺寸和肋板分布示意图如图2所示。

(a) 负泊松比肋板示意图

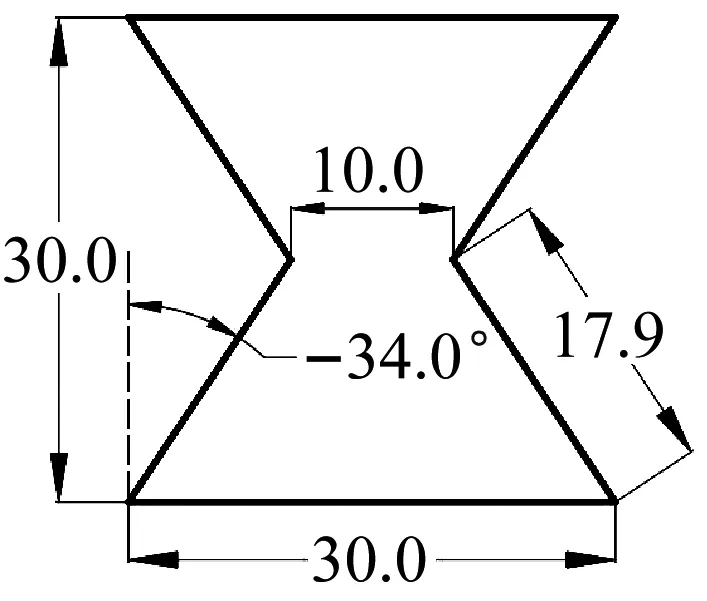
(b) 单胞尺度

采用2D壳单元建立的双层板有限元模型，如图3所示。上、下面板的厚度设置为6 mm，肋板的胞元板厚设置为3 mm。材料参数包括：杨氏模量E=210 GPa、泊松比μ=0.3、密度ρ=7 850 kg/m3。边界条件设定为约束上、下面板四边节点三向位移。

图3 双层板有限元模型

由式(1)～式(4)，可得单胞的等效力学性能参数，如表1所示。

2.2 模态分析

对有限元模型进行模态分析，可得双层板前5阶固有频率如表2所示，部分振型云图如图4所示。

表1 内六角蜂窝单胞的力学性能参数

表2 双层板前5阶固有频率

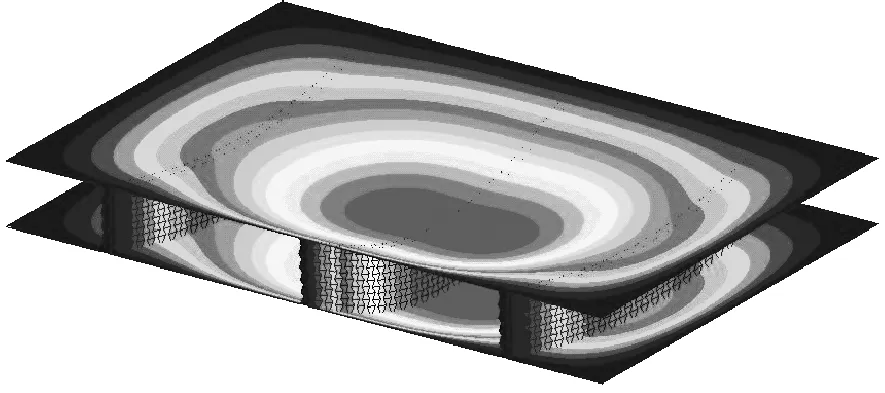
(a) 第1阶云图(48.56 Hz)

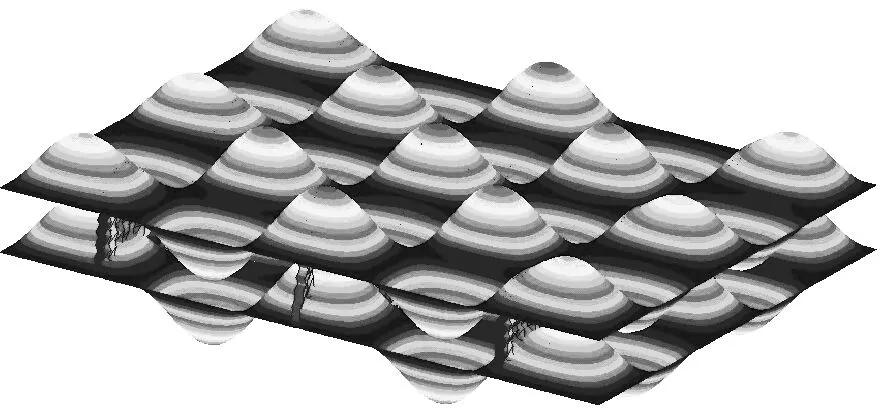
(c) 第60阶云图(526.97 Hz)

从结构固有频率与振型云图分布规律来看，由于负泊松比肋板的刚度值较低，与肋板连接的面板局部区域刚度的增强并不显著，所以在低频范围内，双层板以整体的垂向弯曲模态为主，上、下面板的振型与单层板结构的振型基本一致，且上、下面板之间的振动差异性也并不显著，表明负泊松比肋板在低频时具有较好的振动传递特性。

随着频率的提升，负泊松比肋板的局部模态特征会逐渐凸显，除了垂向弯曲振动，负泊松比肋板在中高频段还出现了明显的横向和纵向上的耦合振动模态。该现象表明在中高频范围内负泊松比肋板局部模态特征更容易被激发，局部变形会更加显著，能够更好地发挥多孔结构易于转化和衰减振动能量的性能优势。

2.3 双层板面板振动响应特性

对上面板施加100 Pa的均布动压载荷，选用模态叠加法进行频率响应分析，计算频段为1～2 000 Hz，步长为2 Hz。考虑到结构的对称性，在上、下面板平面内选取的评价点位置分布如图5所示。

提取各组评价点加速度，按式(5)和式(6)分别计算上、下面板评价点的加速度级及平均振级。

(5)

(6)

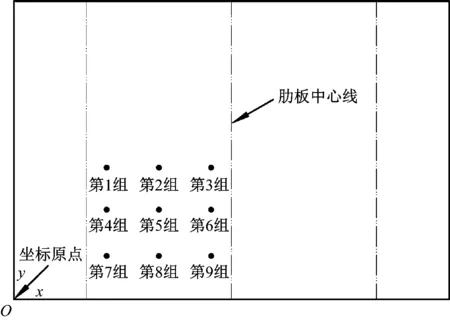
图5 评价点位置分布

定义上、下面板间的平均加速度级之差为上、下面板的振级落差。得到上、下面板的平均加速度级曲线和振级落差曲线分别如图6和图7所示。

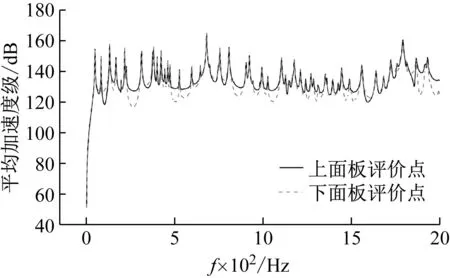
图6 上、下面板平均加速度级曲线

图7 上、下面板振级落差曲线

从图6可见，上、下面板的加速度级差异与结构的谐振频率关系密切。在1～2 000 Hz内，上、下面板的平均加速度级曲线存在多个响应峰值，在谐振频率处，上、下面板的平均加速度级差异较小。在相邻谐振频率之间，上、下面板响应加速度级的差异明显，大部分下面板响应值均低于对应频率的上面板响应值，体现出较为理想的减振效果。

从图7可见，在大多数频段内，上、下面板之间的振动响应存在比较明显的传递衰减，下面板的振动响应得到了有效控制。

2.4 肋板阻尼对振动特性的影响

提升结构阻尼是工程中减振降噪的常用方法之一，多孔结构因为存在更多可利用的孔隙空间，为实施阻尼措施提供更多便利。通过在胞元孔隙间填充轻质橡胶或PUR泡沫[15]、在胞元壁面贴附粘弹性阻尼材料等方法可以有效提升负泊松比肋板的结构阻尼。

本研究中将负泊松比肋板的材料阻尼系数设置为0.5，用于模拟阻尼材料对负泊松比肋板结构阻尼的提升。对比得到肋板有、无阻尼时的上面板平均加速度级、下面板平均加速度级、振级落差曲线分别如图8～图10所示。

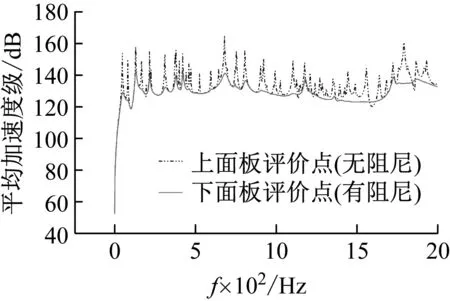
图8 上面板平均加速度级对比曲线

图9 下面板平均加速度级对比曲线

图10 振级落差对比曲线

从图8和图9可见，结构阻尼对振动响应的主要作用体现在大幅削减响应峰值，该“削峰”作用的效果与频率有一定关联，500～2 000 Hz的中高频段“削峰”效果相比500 Hz之前的低频段会更加突出，低频段多以降低响应峰值为主，而中高频段则能够大幅削弱绝大多数的响应峰。在整个计算频段内，在阻尼的“削峰”作用下，整个加速度级响应曲线变得平稳，有效提升了振动控制效果。

从图10可见，阻尼对提升上、下面板间振级落差具有积极作用，且随着频率值的提升，振级落差提升效果更明显。在500 Hz之后的中高频段内，振级落差曲线的大幅振荡现象得到了很有效的控制，在900～1 300 Hz内，有阻尼振级落差值相比无阻尼情形得到了更加明显的提升。

对上、下面板的测点平均加速度在计算频段内计算加速度总级，得到在肋板有、无阻尼两种情形下，上、下面板评价点的加速度总级，如表3所示。由表3可见，增大负泊松比肋板的结构阻尼能够有效控制上、下面板的响应加速度总级，有助于增强负泊松比肋板对振动的损耗衰减能力。

表3 肋板有、无阻尼情形下上、下面板加速度总级

3 肋板刚度对声振特性的影响

本章主要分析负泊松比肋板胞元的厚度与宽度变化对双层板的声振特性的影响。

3.1 对比算例结构参数

保持肋板结构总质量不变，以肋板中心线为基准，调整负泊松比肋板宽度与胞元壁厚，并与等质量的平板构成的实肋板模型对比，设计了4个对比模型，其各自肋板参数如下：① 对比模型1，肋板宽度20 mm、胞元壁厚3 mm；② 对比模型2，肋板宽度40 mm、胞元壁厚1.5 mm；③ 对比模型3，肋板宽度60 mm、胞元壁厚1 mm；④ 对比模型4，6.31 mm厚的等质量平板肋板。

对比模型中负泊松比肋板的胞元层数均为5层，单胞的结构尺寸为底边宽度30 mm、高度30 mm、特征角-34°。

按照式(1)～式(4)计算得到的不同模型内六角蜂窝胞元的力学参数如表4所示。

表4 内六角蜂窝单胞的力学性能参数

3.2 肋板结构参数对静力学性能的影响

考虑使用负泊松比超材料肋板后双层板的结构强度问题，在上面板施加大小为100 Pa的均布压力载荷，肋板参数改变时静力学分析结果，如表5所示。

从表5可见，超材料肋板双层板结构刚度相比于实肋板双层板结构有一定削弱，在静压力作用下，其最大位移与最大应力均大于常规实肋板双层板结构。随着肋板宽度的增大，超材料肋板的刚度因板厚减小而受到相应削减，最大静位移逐步提升。对于超材料肋板双层板而言，肋板宽度变小时，在肋板与面板连接区域、面板约束边界附近更容易产生应力集中现象，因此其最大应力值会偏大。

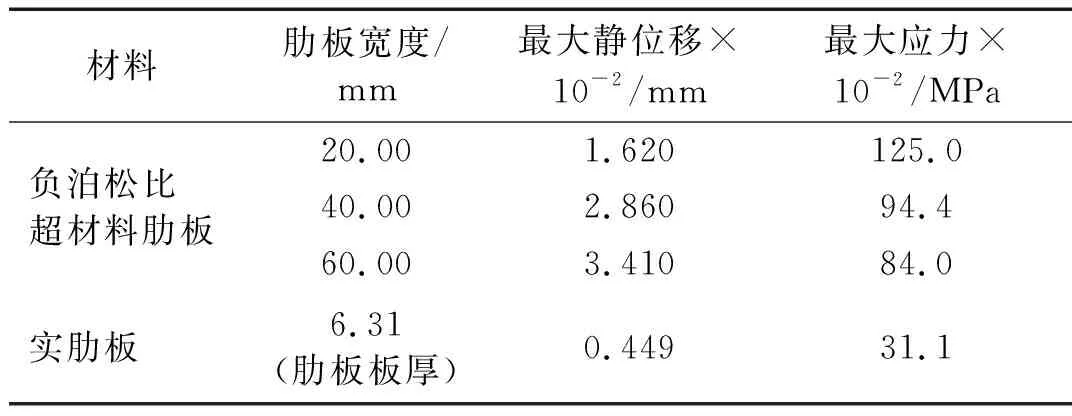
表5 不同肋板形式双层板结构静力学分析结果

3.3 肋板刚度对面板振动特性的影响

使用模态叠加法进行频率响应分析，计算频段为1～3 500 Hz，步长为2 Hz，计算得到各对比模型的上面板加速度级、下面板加速度级、振级落差曲线分别如图11～图13所示。

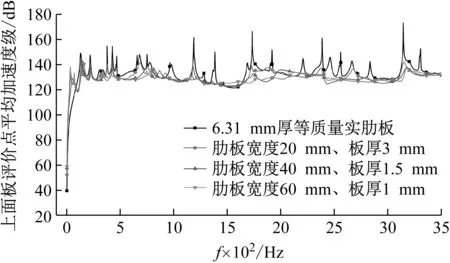
图11 上面板评价点平均加速度级曲线

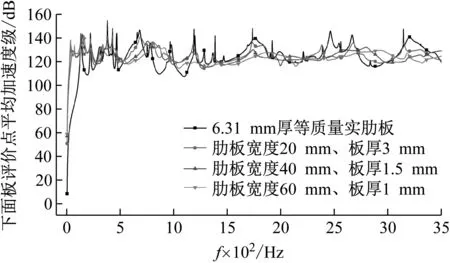
图12 下面板评价点平均加速度级曲线

从图11和图12可见，负泊松比肋板与实肋板双层板之间的振动响应差异与频率有关。由于实肋板刚度较大，其第一阶响应峰频率相比负泊松比肋板的双层板要高。在110 Hz以下的低频区间内，提升肋板刚度可以有效减小振动响应，但对比响应峰值，高刚度的实肋板没有体现出类似优势。随着频率增大，负泊松比肋板的作用会逐渐凸显。在110～500 Hz间，负泊松比肋板与实肋板模型的上面板响应曲线基本类似，但是下面板响应差异较大，含负泊松比肋板的双层板上、下面板响应峰值均比实肋板双层板响应小。在500 Hz以上的频率区间，负泊松比肋板模型的响应峰值相比于实肋板模型明显减小，平均加速度级曲线更加平稳。这说明负泊松比肋板在这些频段对振动能量有良好的吸收和衰减功能，能更好地控制面板的振动响应。

图13 上、下面板振级落差曲线

对比不同厚度的含负泊松比肋板的双层板的振动响应，可见负泊松比肋板的胞元厚度越小，面板的响应峰值也越小。从表4可见，厚度越小的负泊松比肋板，其等效弹性模量和剪切模量越低，因此刚度越低，可以更好地发挥低刚度多孔肋板的减振性能。

从图13可见，在1 500 Hz之前的频段范围内，实肋板的振级落差在多数情况下会更大，尤其是在面板响应谷值附近的频段，实肋板算例的上、下面板间加速度响应差异会更显著。由于实肋板刚度大，上面板上有、无肋板支撑的两类区域刚度差异明显，上面板无肋骨支撑区域振动能量在总能量占比较高，通过实肋板传递至下面板的振动能量较少，导致振动能量在上、下面板间的分配不均衡。相比之下，负泊松比肋板刚度较小，上面板有、无肋骨支撑区域刚度差异没有实肋板显著，振动能量经由负泊松比肋板传递后，上、下面板的振动能量分配的更均衡。在1 500 Hz以后的频段范围内，实肋板在振级落差上已经没有明显优势，负泊松比肋板因为能够更好地分担与吸收振动能量，从而表现出更稳定的减振效果，振级落差曲线的波动相比实肋板更加平缓。

依据式(7)计算4个对比模型上、下面板评价点在1～3 500 Hz内的加速度总级，具体结果如表6所示。

分析表6中数据，在控制质量和激励不变时，负泊松比肋板模型的上、下面板的加速度总级均显著低于实肋板模型，实肋板不能够像多孔的负泊松比肋板一样易于产生形变，导致振动能量主要集中在两个面板上，同时实肋板算例的上面板振动要比下面板振动剧烈更多，加速度总级在计算频段内差异更明显。

表6 对比模型上、下面板加速度总级表

对比不同参数的负泊松比肋板算例，在总质量不变的条件下，当负泊松比肋板的刚度减小时，上、下面板的加速度总级随之同时减小，负泊松比肋板以应变能的形式吸收转化的振动能量会更多。同时低刚度有利于增大上、下面板加速度总级的差值，提升减振性能表现，更好地达到减振的设计目的。

3.4 肋板刚度对面板声学特性的影响

使用直接边界元法计算3.1节各对比算例面板声辐射，将Patran中面板所有节点的速度响应以op2文件格式导出至LMS Virtual.Lab中作为声学边界条件，计算所得的4个对比算例在1～3 500 Hz内的辐射声功率曲线如图14所示。

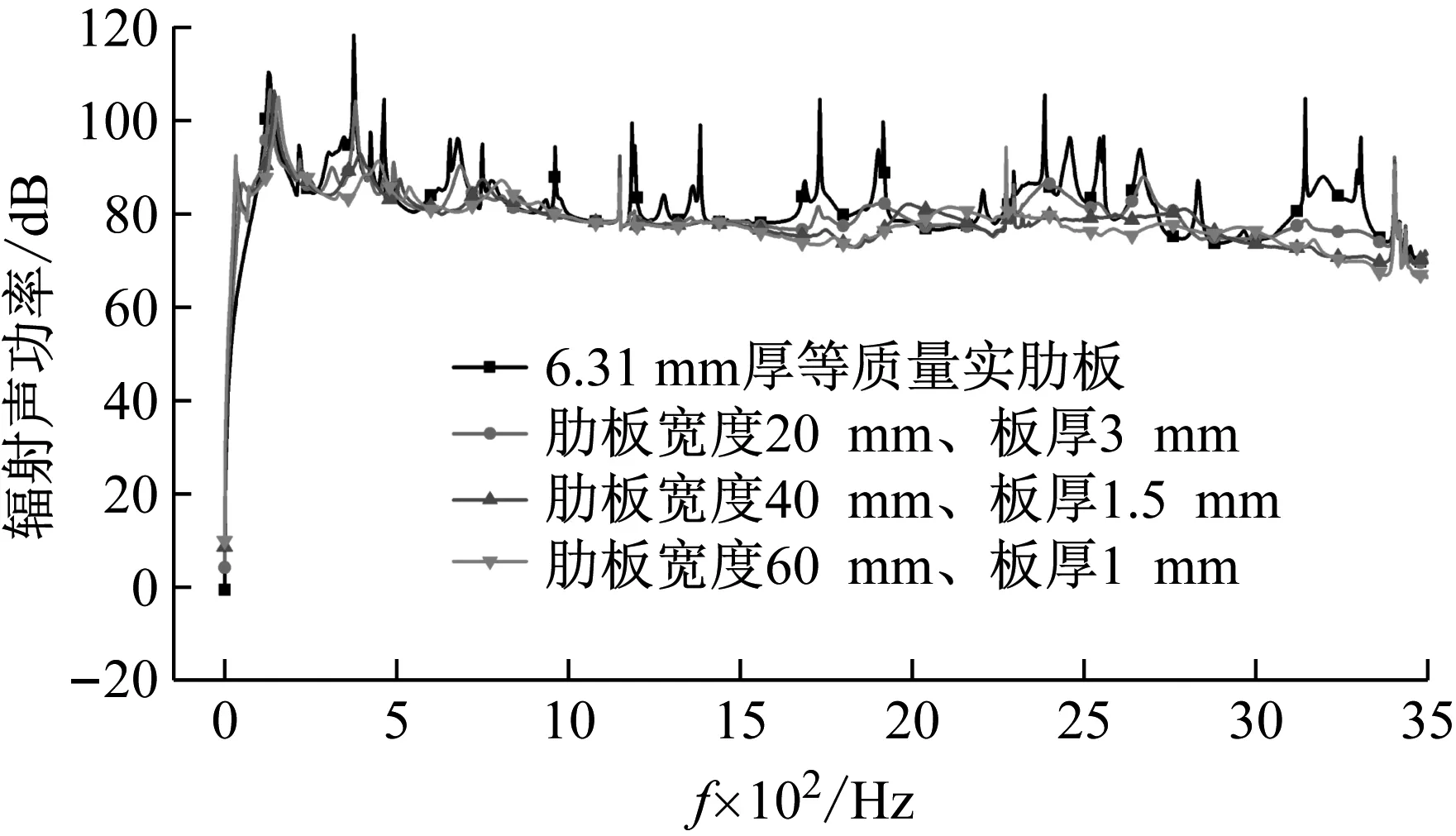
图14 双层板辐射声功率对比曲线

从图14可见，与面板振动响应曲线类似，实肋板与负泊松比肋板对比算例的辐射声功率曲线差异主要体现在峰值位置附近，且随着频率值的提升，这种差异性表现得更加明显。在1～200 Hz内，由于负泊松比肋板刚度小，各阶固有频率整体偏低，辐射声功率曲线先出现峰值。在200～1 500 Hz内，实肋板算例的辐射声功率曲线具有更多的峰值，而负泊松比肋板算例的曲线则相对平缓，且肋板刚度越小，辐射声功率曲线峰值越小。在1 500～3 500 Hz频段的大部分频点上，实肋板算例的辐射声功率明显高于负泊松比肋板算例。该频段内负泊松比肋板算例的辐射声功率维持在80 dB附近，肋板刚度削弱时，曲线更平稳。整体上负泊松比肋板构成的双层板辐射声功率比实肋板结构要低，且负泊松比肋板的板厚越小，层间结构的等效模量越低，辐射声功率也越低。

4 结 论

本文主要研究了含内六角形负泊松比超材料肋板的双层板振动与声辐射特性，探讨了结构阻尼、肋板刚度等参数对声振特性的影响，主要结论包括：

(1) 双层板上、下面板间采用负泊松比肋板连接后，下面板响应相比上面板有一定的衰减。在负泊松比肋板中增加阻尼后能起到较好削弱面板响应峰的效果，且在高频范围内更加明显，同时上、下面板之间的振级落差也有一定的增大。

(2) 控制肋板总质量不变时，负泊松比肋板构成的双层板结构上、下面板加速度均显著低于传统实肋板结构，实肋板不能像多孔的负泊松比肋板一样易于吸收转化振动能量。对于负泊松比肋板构成的双层板而言，增大肋板宽度、减小肋板厚度可以降低等效模量，更好地削减双层板面板的振动响应峰值，有助于提升双层板减振效果。

(3) 不同肋板参数的辐射声功率曲线与振动响应曲线有类似规律特征，负泊松比肋板构成的双层板辐射声功率比实肋板结构要低，且负泊松比肋板的板厚越小，层间结构的等效模量越小，辐射声功率也越低。