反共振双层隔振系统分析

张赣波， 赵 耀

(华中科技大学 船舶与海洋工程学院， 武汉 430074)

经典双层隔振理论建立在Snowdon等[1-2]的研究工作上。相比于单层隔振，双层隔振传递曲线在隔振区以2倍斜率下降而被普遍应用于舰船发电机组、通风机组等辅机隔振装置中[3]。在无阻尼理想条件下，双层隔振传递率在隔振区可达到-24 dB/Oct的最大衰减速率，但为抑制共振峰，一定阻尼必不可少，这反过来将减小传递曲线下降斜率，损失中高频隔振效果。因此，单纯提高阻尼抑制共振峰在双层隔振系统设计中并不可取，应发展一种可抑制共振峰，但又不降低隔振区传递率衰减速率的新方法。

准零刚度隔振器因具有“高静低动”的非线性刚度特性而受到广泛关注，但研究表明其隔振性能同样受阻尼困扰。文献[4-5]分别针对准零刚度单层和双层隔振系统传递率进行过理论推导，结果显示共振峰值和隔振区传递曲线下降斜率受阻尼的影响效果也是相反的。

Karnopp等[6]曾提出天棚阻尼概念，假想阻尼的一个端点在惯性坐标系上，这样阻尼力与另一个端点的绝对速度成正比。这种虚拟的单端点阻尼可采取半主动的开关控制策略实现，在共振区打开阻尼，而在隔振区关闭阻尼，达到有效抑制共振峰而不降低隔振区传递率衰减速率的目的，很好地解决隔振系统中阻尼的设计矛盾。Griffin等[7]提出以动力吸振器作为天棚阻尼的被动实现方法，基于共振峰和隔振区传递率衰减双重目标进行优化计算，隔振效果取决于质量比，较大的质量比带来的问题是被隔振设备承载很大的动力吸振器质量。文献[8]将磁流变阻尼器作为船舶辅机双层隔振系统的半主动控制装置，理论分析结果指出在半主动控制下增大磁流变阻尼器的阻尼可明显抑制主共振峰值，同时对非共振区传递率影响较小，但论文未提及半主动控制算法。

反共振隔振器(anti-resonant vibration isolator，AVI)是一类具有反共振特性的隔振器，融合吸振和隔振的技术特点，其基本原理是在隔振器中引入双端点性质的惯性元件，利用惯性元件的惯性力抵消弹性元件的弹性力[9]。Smith[10]对这类双端点性质的惯性元件进行理论化，首次提出“惯容”概念。因具有两个端点，惯容与弹簧元件进行串、并联连接，按一定的结构规律就可以构成AVI[11]。因增加惯性，AVI可降低隔振系统的固有频率[12]。

基于反共振特性，本文提出以AVI进行双层隔振系统设计，解决其阻尼矛盾问题，在共振区抑制共振峰值，在隔振区维持双层隔振传递率衰减速率，以改善双层隔振性能。由于AVI存在不同的结构形式，本文先针对三型单惯容AVI开展结构选型分析，在优化参数条件下与传统隔振器进行双层隔振特性比较，优选出适用的二级串联型三元件AVI结构；根据传递曲线存在与阻尼无关的固定点，建立了反共振双层隔振系统的调谐优化方法，分别得到了AVI安装于上层和下层两种方式下的动力参数优化数值解，并在调谐优化状态下进行上层和下层反共振隔振效果比较；最后讨论了传统隔振器阻尼的影响，提出了反共振双层隔振系统的阻尼设计方案。

1 双层隔振系统传递函数

双层隔振系统模型如图1所示。由传递矩阵方法，列写出设备和基础的力和响应的传递矩阵方程

(1)

式中:F，X分别为力和响应复幅值；Z为位移阻抗；下标m，i，f分别为设备和中间体、隔振器、基础。

求解式(1)得

(2)

代入基础阻抗Zf至式(2)，整理得力传递函数

(3)

在基础刚性条件下，式(3)简化为

(4)

式(4)表明，隔振器阻抗特性决定双层隔振系统的隔振特性，体现在两方面：一是隔振器阻抗函数的零点对应于隔振系统的反共振特性；二是Zm1Zm2与Zi1Zi2的阶数差对应于传递曲线在隔振区的下降斜率，决定中高频隔振效果。

为以示区分，本文将基于“弹簧-阻尼”结构体系的隔振器称之为传统隔振器(conventional vibration isolator，CVI)，其阻抗函数无零点，因而无反共振特性。AVI建立在“惯容-弹簧-阻尼”结构体系下，利用惯容惯性力和弹簧弹性力在共振状态下等值反向相互抵消形成反共振，抑制共振峰值。

2 AVI结构选型

单惯容元件可以综合三型AVI结构，如图2所示。记作AVI-Ⅰ，AVI-Ⅱ，AVI-Ⅲ。若图2中K为CVI，AVI-Ⅰ，AVI-Ⅱ，AVI-Ⅲ为在CVI结构上分别并联单惯容、串联“惯容-弹簧”二元件并联支路和并联“惯容-弹簧”二元件串联支路。

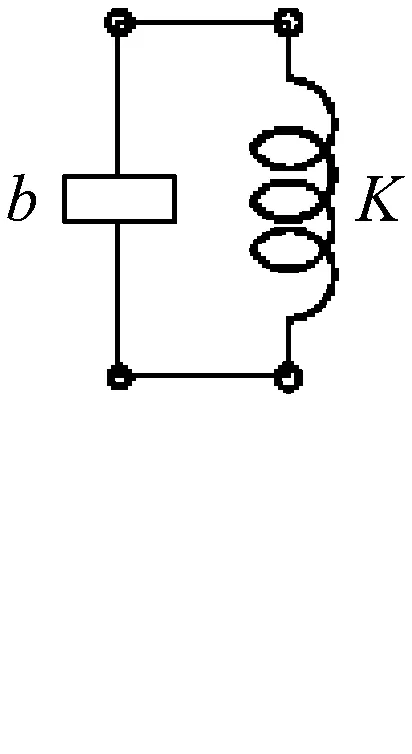
AVI-Ⅰ

AVI-Ⅰ，AVI-Ⅱ，AVI-Ⅲ阻抗分别为

(5)

式中：b为惯质；k，K为刚度；s为复变量。当AVI-Ⅰ，AVI-Ⅱ，AVI-Ⅲ作为上、下层隔振装置时，b，k，K分别加以下标1，2表示。

将设备和中间体看作刚体，质量分别以M1，M2表示，则Zm1=M1s2，Zm2=M2s2。当AVI-Ⅰ同时作为上、下层隔振装置时，Zi1Zi2=(b1s2+K1)(b2s2+K2)是4阶多项式，与Zm1Zm2=M1M2s4阶数相同，传递曲线在隔振区将接近于一水平渐近线而无衰减。即使仅作为一层隔振装置，力传递函数分母多项式和分子多项式的阶数差也仅有2阶，隔振区传递率衰减速率为-12 dB/Oct，相当于单层隔振水平。因此，AVI-Ⅰ不适用于双层隔振。

对于AVI-Ⅱ，AVI-Ⅲ，其阻抗分母多项式和分子多项式具有相同的阶数，作为双层隔振装置时，代入式(4)将不改变力传递函数的阶数差，因而也不影响传递曲线的下降斜率，适用于双层隔振。

以下针对AVI-Ⅱ，AVI-Ⅲ作进一步结构优选。制定比较方案：以传统双层隔振系统M1-K1-M2-K2为参照对象，刚度比λ=K2K1和质量比u=M2M1按两固有频率比值最小化设计，满足λ=1+u；将AVI-Ⅱ，AVI-Ⅲ替换K1，K2，共有8种上、下层隔振器组合方案，分别与参照对象进行隔振特性比较。

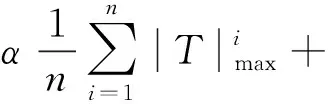
(6)

式中：n为共振峰数量；α为加权系数，取α=0.5。

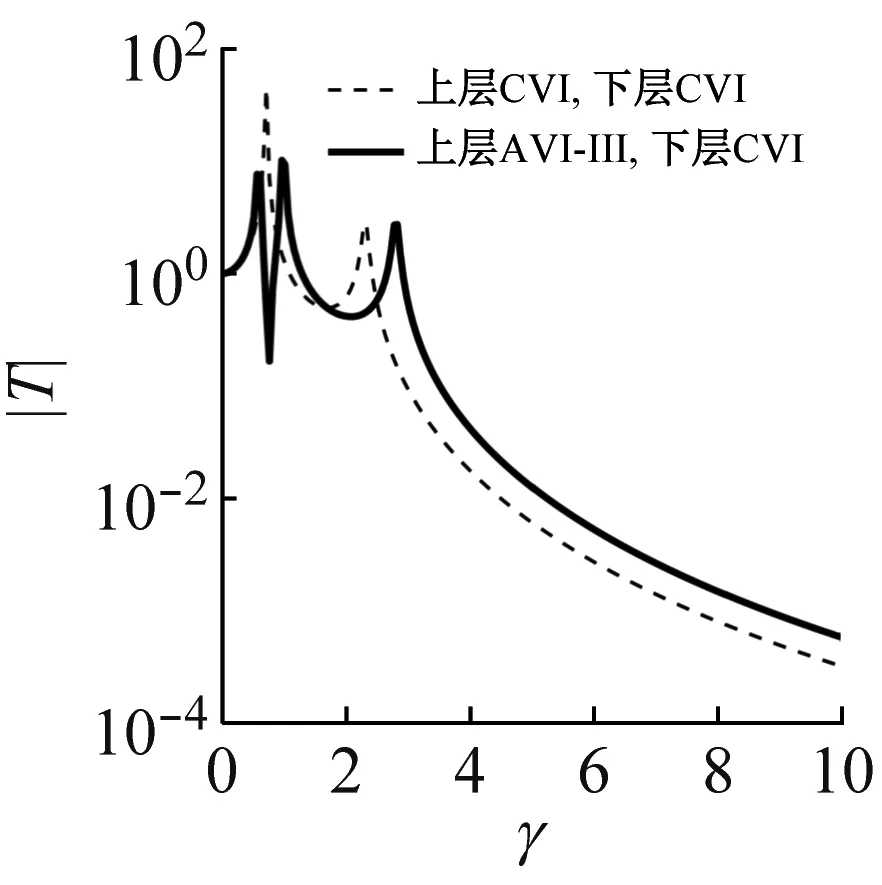
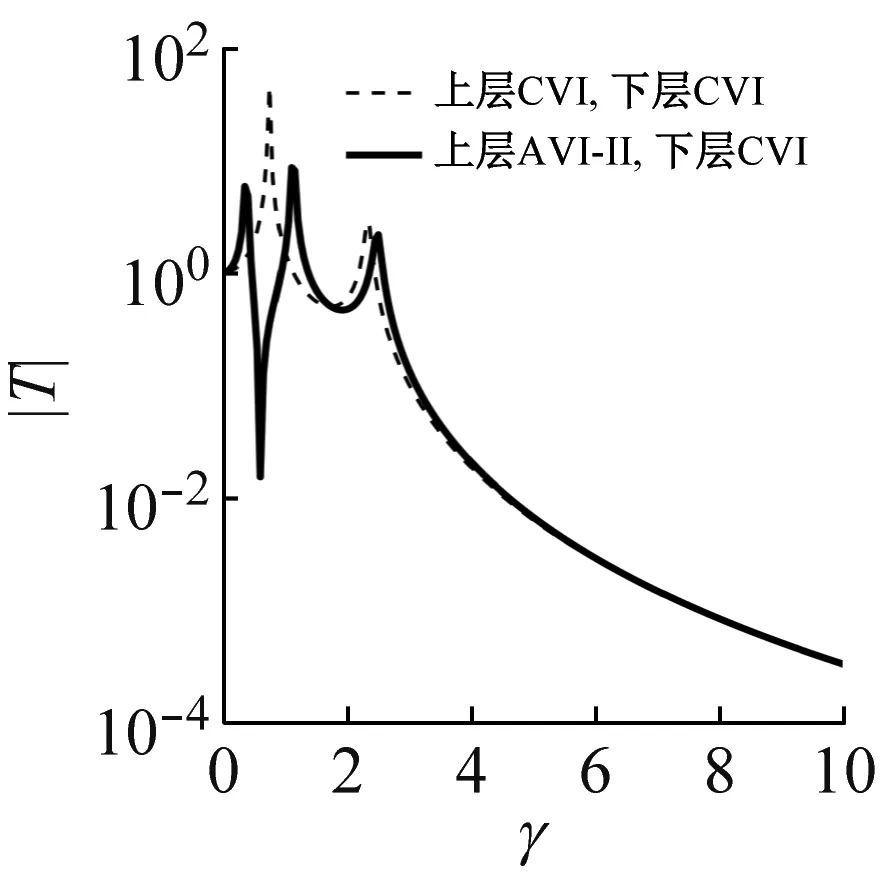
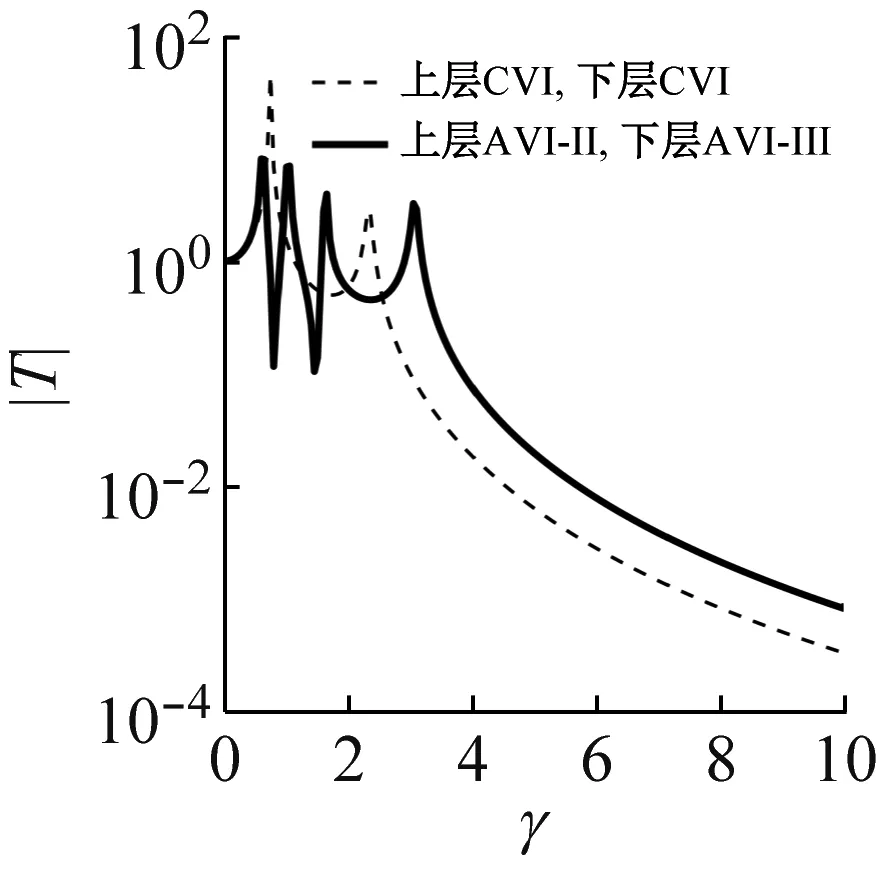
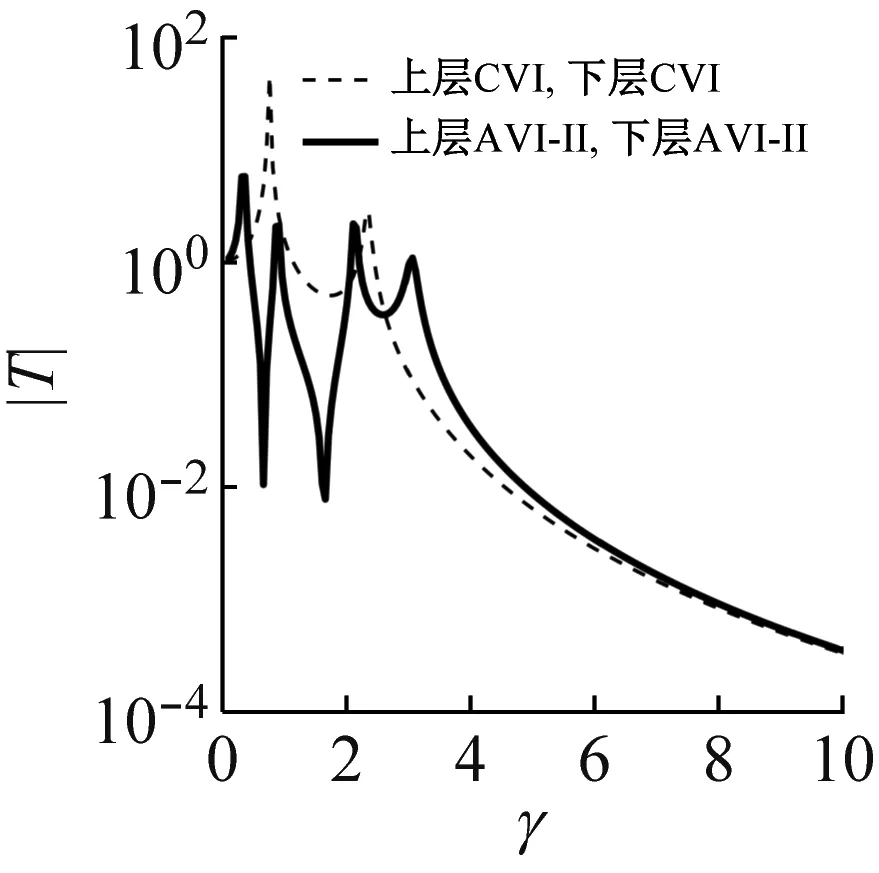
采用粒子群优化算法搜寻优化变量值[13]。作为示例，取u=0.5，λ=1.5，根据优化变量值得到不同隔振器组合方案下传递特性，如图3所示。观察图3，反共振隔振系统传递曲线都有典型的反共振峰。AVI-Ⅱ，AVI-Ⅲ无论作为上层、下层或双层隔振装置，其传递曲线在越过共振区后的衰减斜率均与CVI相当，但传递率幅值存在差异。其中，AVI-Ⅲ对应的传递率幅值高于CVI，而AVI-Ⅱ与CVI基本一致。因此，AVI-Ⅱ更有结构优势，本文以AVI-Ⅱ开展双层隔振系统反共振设计分析。

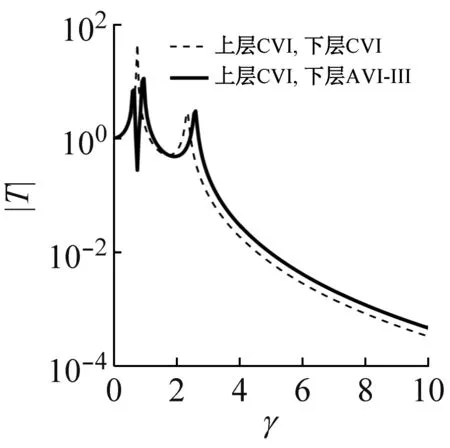
(a)

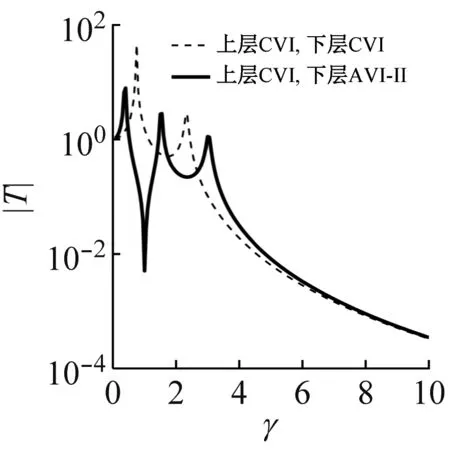
(b)

(c)

(d)

(e)

(f)

(g)

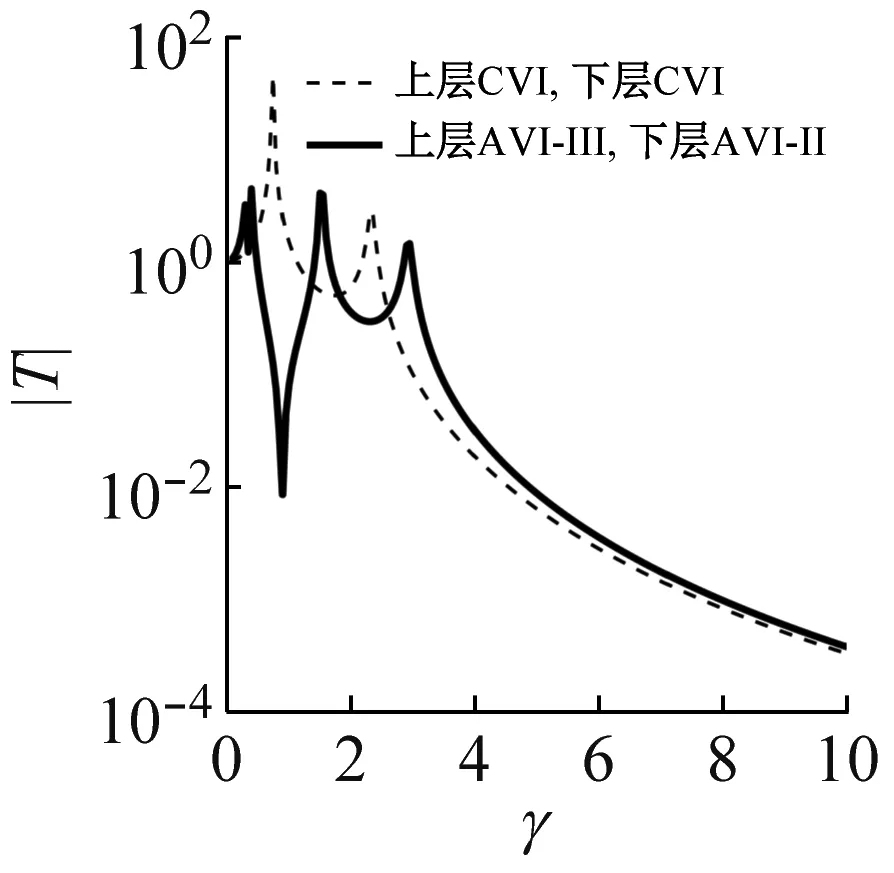
(h)

为抑制隔振系统的共振峰值，在AVI-Ⅱ结构中应增加阻尼元件。根据阻尼与惯容、弹簧的组合规律，并联阻尼不破坏惯容和弹簧的反共振特性。为此在AVI-Ⅱ中引入并联阻尼元件，见图4中虚线所示，共有3种不同排列方式。

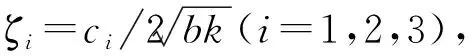
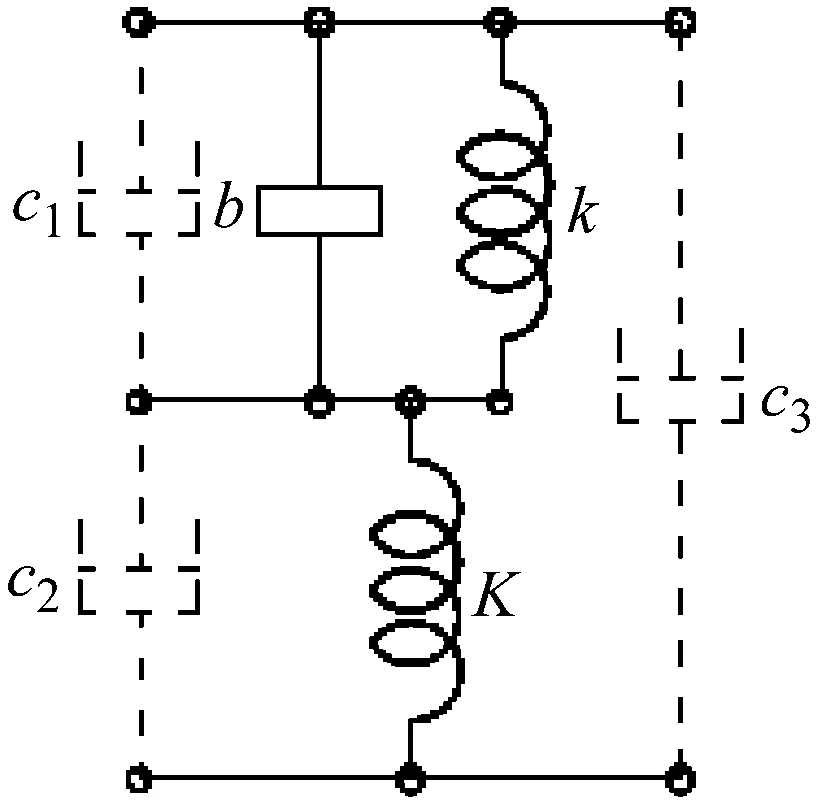
图4 阻尼在AVI-Ⅱ中的排列方式

3 AVI动力参数设计

3.1 固定点

由图3可知，在双层隔振系统中设置一层或双层AVI-Ⅱ都可以抑制原第1阶共振峰。与一层AVI-Ⅱ相比，上下双层AVI-Ⅱ有助于进一步改善隔振性能，如抑制原第2阶共振峰，但考虑到AVI-Ⅱ是二级串联型结构，二级弹簧k，K串联的合成刚度小于K，使得隔振系统的静位移有所增大，尤其在上下双层AVI-Ⅱ时静位移增加量会更大。兼顾隔振系统稳定性，本文研究上下一层AVI-Ⅱ情形，另一层仍采用CVI。

在AVI-Ⅱ结构中并联阻尼c1，忽略CVI阻尼。当AVI-Ⅱ作为上层隔振装置时，根据第2章定义无量纲量，由式(4)推导无量纲力传递函数为

(7)

同理，可推导出AVI-Ⅱ作为下层隔振装置时的无量纲力传递函数为

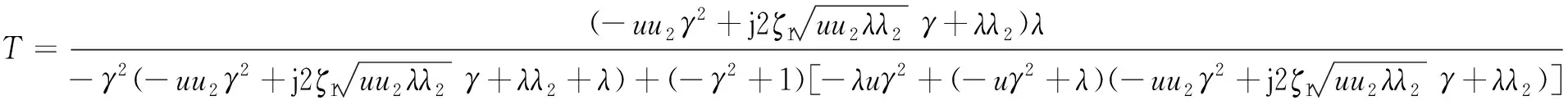
(8)

根据式(7)和式(8)，力传递函数将整理成如下形式

(9)

式中，Nr(γ)，Ni(γ)，Dr(γ)，Di(γ)都为关于γ的函数，并且与阻尼比ζ1无关。

考虑阻尼比ζ1的两极限情况。

当ζ1=0时，有

(10)

当ζ1→∞时，有

(11)

对于任意阻尼比ζ1，将式(9)进一步整理为

(12)

传递曲线Tζ1与Tζ1→∞存在交点，假设交点P，其横坐标γP，代入式(11)和式(12)，有

(13)

对照式(10)、式(11)和式(13)可知，Tζ1=0=Tζ1→∞成立。这说明交点P也是传递曲线Tζ1=0与Tζ1→∞的交点。因此，交点P是传递曲线Tζ1与阻尼比ζ1无关的固定点，其横坐标γP由式(13)唯一确定。

以AVI-Ⅱ作为上层隔振装置为例，Tζ1=0=Tζ1→∞整理后是关于γ的6次方程，有3个解，故传递曲线Tζ1存在3个与阻尼比ζ1无关的固定点。这3个固定点，分别以P，Q，S表示，如图6所示。对于AVI-Ⅱ作为下层隔振装置，固定点特征与之相似。

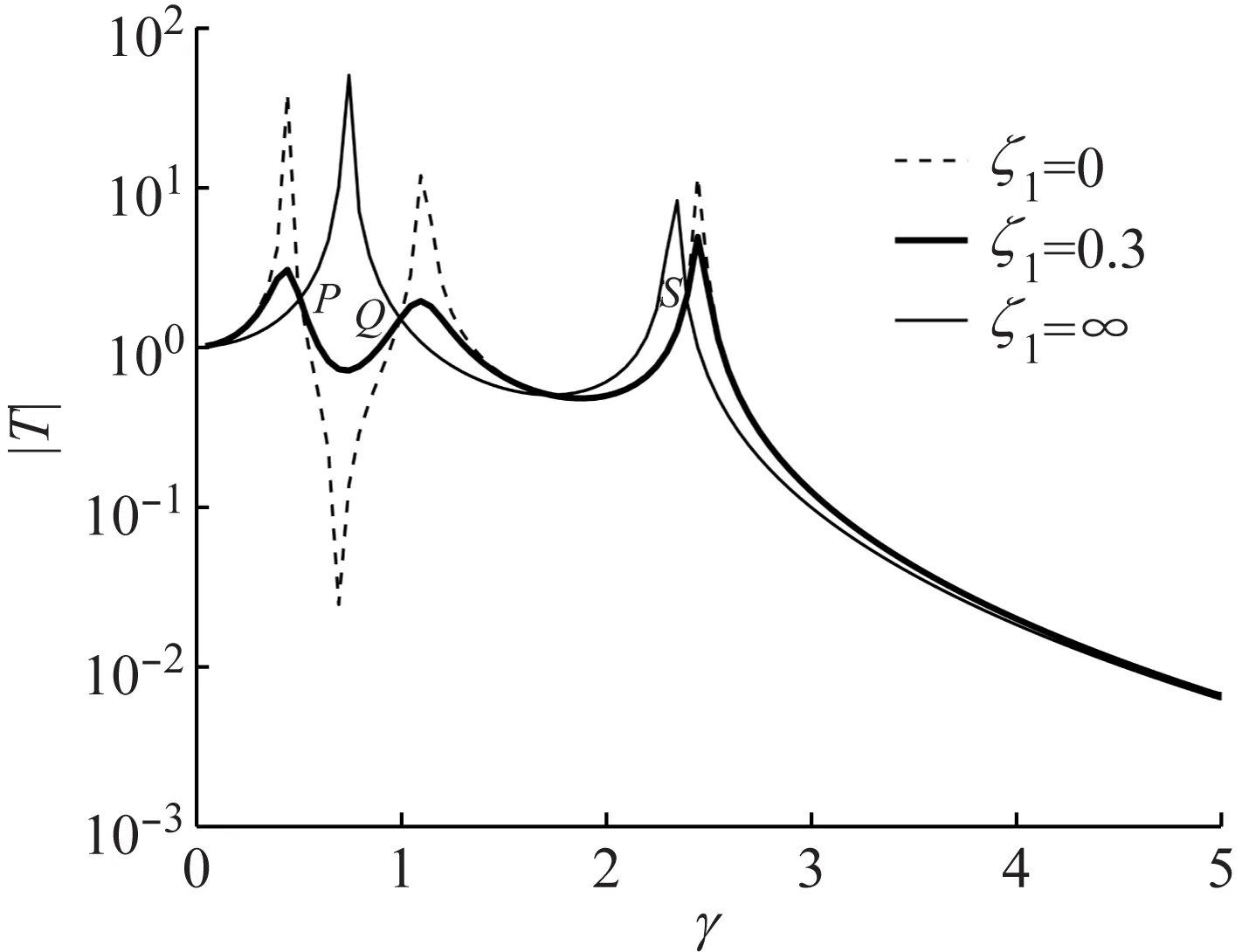
图6 传递曲线固定点

3.2 动力参数优化

3.2.1 调谐优化方法

基于固定点对AVI-Ⅱ动力参数进行调谐优化设计，其基本步骤是：先令两固定点P，Q的幅值相等，确定最优刚度比；再令两固定点P，Q为极大值点，确定最优阻尼比[14]。

以上层反共振隔振说明。由图6可知，两固定点P，Q都在传递率曲线Tζ1=0，Tζ1→∞的相反边上，相位相反，根据Tζ1=0=Tζ1→∞有

Nr(γ)Di(γ)+Ni(γ)Dr(γ)=0

(14)

根据式(7)对Nr(γ)，Ni(γ)，Dr(γ)，Di(γ)具体化，代入式(14)，整理式(14)得关于γ的6次方程，令α=γ2，将式(14)化简为如下标准型一元三次方程

(15)

式中，x，y，z，w为关于u，λ，u1，λ1的关系式。

采用Cardano公式求解。设α=β-y3x，式(15)转化为

β3+pβ+q=0

(16)

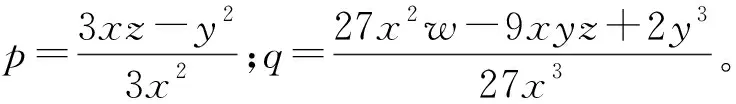
当判别式(q2)2+(p3)3<0时，式(16)有3个不等实根，分别为

(17)

其中

联立式(15)～式(17)，可求解各固定点横坐标γP，γQ，γS。再根据两固定点P，Q在传递曲线Tζ1→∞共振峰的两边，相位也相反，由式(11)得两固定点P，Q幅值相等条件为

(18)

求解式(18)得到最优刚度比λ1opt，由λ，u，u1共同确定。

当两固定点P，Q为极大值点时，满足

(19)

3.2.2 上层反共振隔振优化结果

以u，u1为自变量，λ1，ζ1为因变量，由于方程阶数较高，无法推导出优化解析解表达式，编程计算出其优化数值解。最优刚度比λ1opt和最优阻尼比ζ1opt关于u，u1的等值线，如图7、图8所示。从计算结果看，u1>0.5才有调谐优化解。在u一定条件下，λ1opt与u1成正相关性，而ζ1opt与u1成负相关性，随u1减小，ζ1opt变化灵敏度越大。总体上，ζ1opt受u变化影响很小，λ1opt和ζ1opt主要决定于u1。

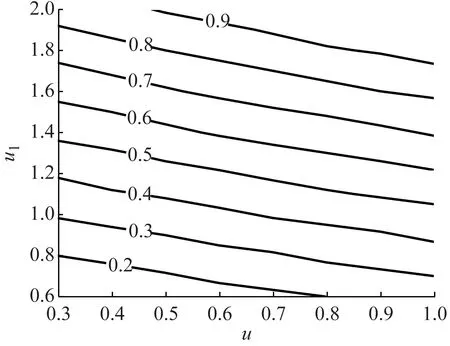
图7 最优刚度比λ1opt关于u，u1的等值线

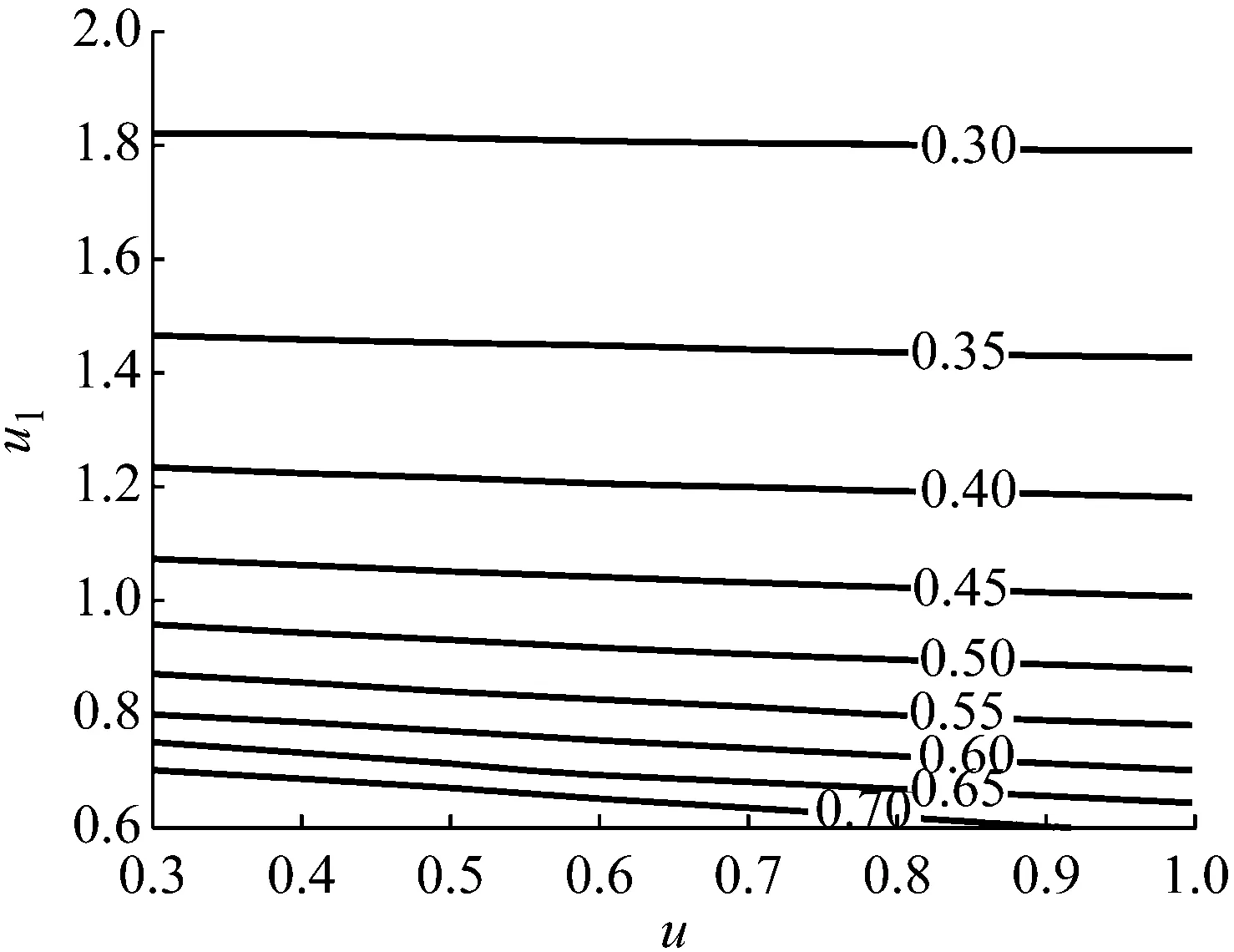
图8 最优阻尼比ζ1opt关于u，u1的等值线

以u=0.5示例，调谐优化后的力传递特性。如图9所示，图9中一并绘制出传统双层隔振系统的力传递曲线。比较可见，原第1阶共振峰在实施反共振隔振后被有效抑制，由尖锐的单共振峰转变为平坦的双共振峰，原第2阶共振峰值也有所降低。在越过共振区之后的隔振区，反共振隔振与传统隔振的传递曲线基本重合，传递率衰减速率无变化，中高频隔振效果无损失。随u1递增，反共振隔振系统共振峰值也随之升高，主要原因在于ζ1opt随u1增大而减小。

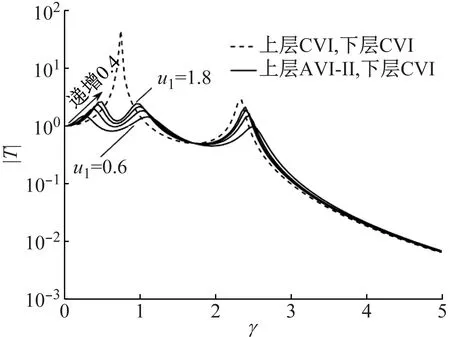
图9 调谐优化后的传递特性

3.2.3 下层反共振隔振优化结果

对于下层反共振隔振，其优化计算结果，如图10、图11所示。从计算结果看，u2>2才有调谐优化解。与上层反共振隔振规律相似，在u一定条件下，随u2增大，λ2opt增大，而ζ2opt减小。λ2opt，ζ2opt与u和u2都存在强相关性，受两者共同影响。当u和u2都较小时，ζ2opt变化较灵敏。

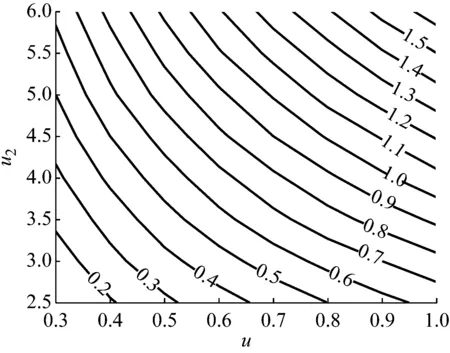
图10 最优刚度比λ2opt关于u，u2的等值线

图11 最优阻尼比ζ2opt关于u，u2的等值线

仍以u=0.5为示例，调谐优化后的力传递特性，如图12所示。下层反共振隔振效果与上层也相似，在维持隔振区传递曲线下降斜率不变化的条件下，实现原第1阶共振峰值的有效抑制；双共振峰值随u2增大而升高，也呈现正相关性。

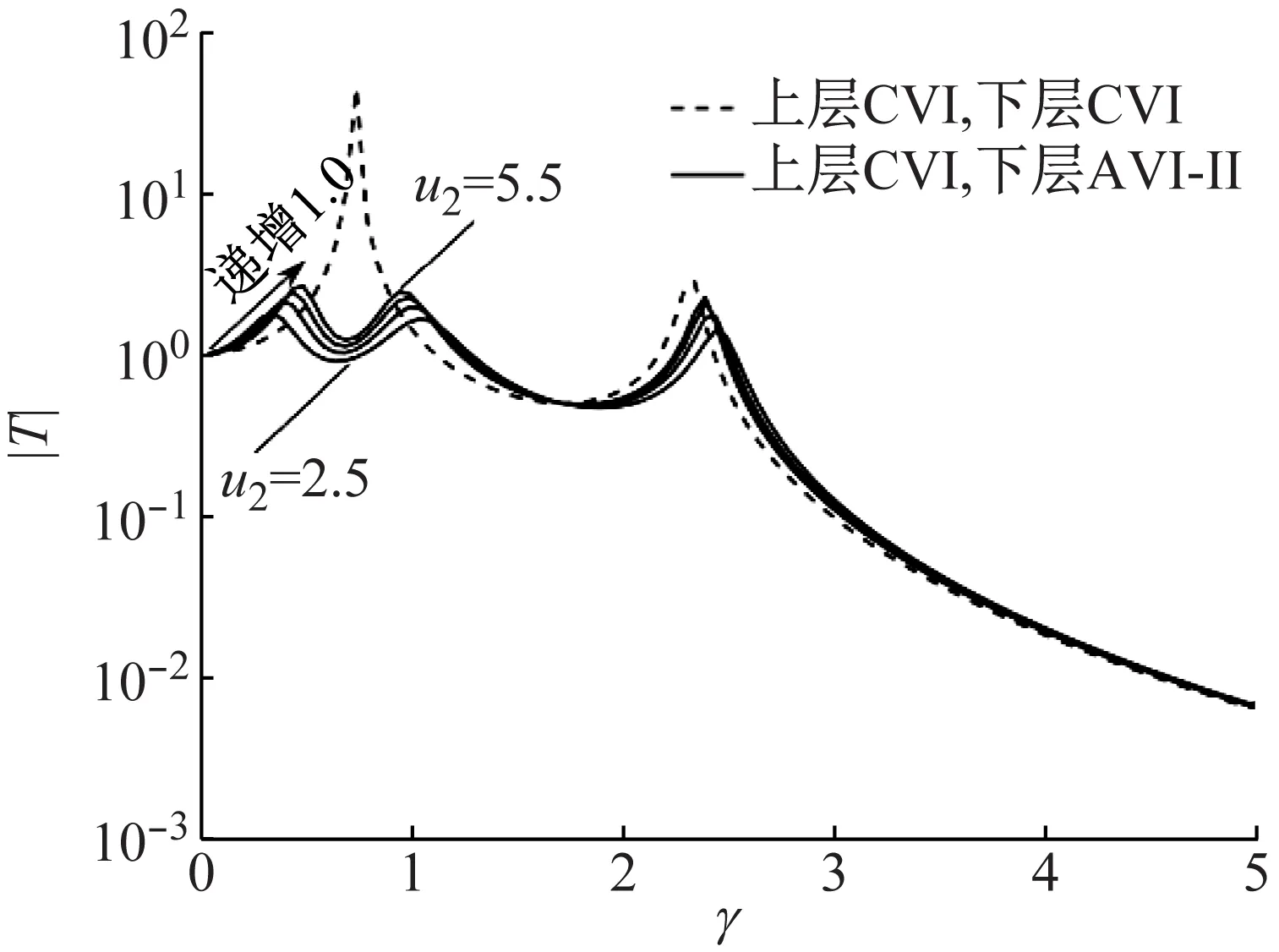
图12 调谐优化后的传递特性

3.3 上层和下层反共振隔振比较

从优化计算结果看，AVI-Ⅱ安装于上层和下层的隔振效果和参数影响规律具有一致性，在u确定后，双共振峰值随u1，u2增大而升高，共振峰抑制效果减弱。

令u1=u×u2(u1>0.5，u2>2)，在同一惯质条件下对上层和下层反共振隔振效果进行比较。在调谐优化状态下，AVI-Ⅱ安装于上层和下层两种方式的双共振峰值比较，如图13所示。图13中计算结果对应于u=0.3，此时双共振峰值最低。直观看出，下层反共振隔振的双共振峰值都低于上层反共振隔振。因此，在工程可行条件下，宜将AVI-Ⅱ作为下层隔振装置。

图13 上层和下层反共振隔振效果比较

4 阻尼影响

第3章分析结果仅考虑AVI-Ⅱ阻尼，而实际上安装于另一层的CVI也存在阻尼，以下进一步分析CVI阻尼对反共振隔振效果的影响。

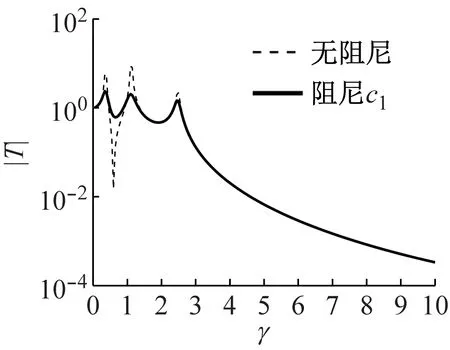
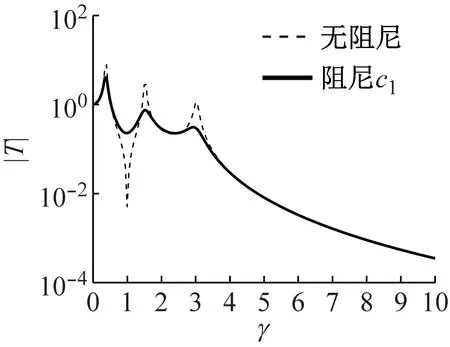
根据调谐优化结果，在u一定时，最优阻尼比ζ1opt，ζ2opt分别与u1，u2成负相关性，为此取u1=2，u2=6进行讨论，此情形下最优阻尼比ζ1opt，ζ2opt较小，以凸显CVI阻尼影响。取u=0.5，上层反共振隔振优化值λ1opt=0.91，ζ1opt=0.28，下层反共振隔振优化值λ2opt=0.92，ζ2opt=0.28。

因此，反共振双层隔振系统合理的阻尼设计方案是：AVI-Ⅱ阻尼以调谐优化值设计抑制共振峰，而CVI阻尼最小化，使得隔振区传递率以接近于理论最大速率衰减。

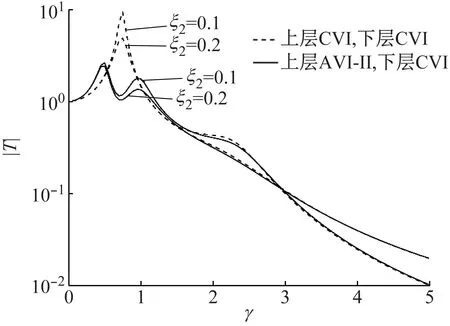
图14 上层反共振隔振时CVI阻尼影响

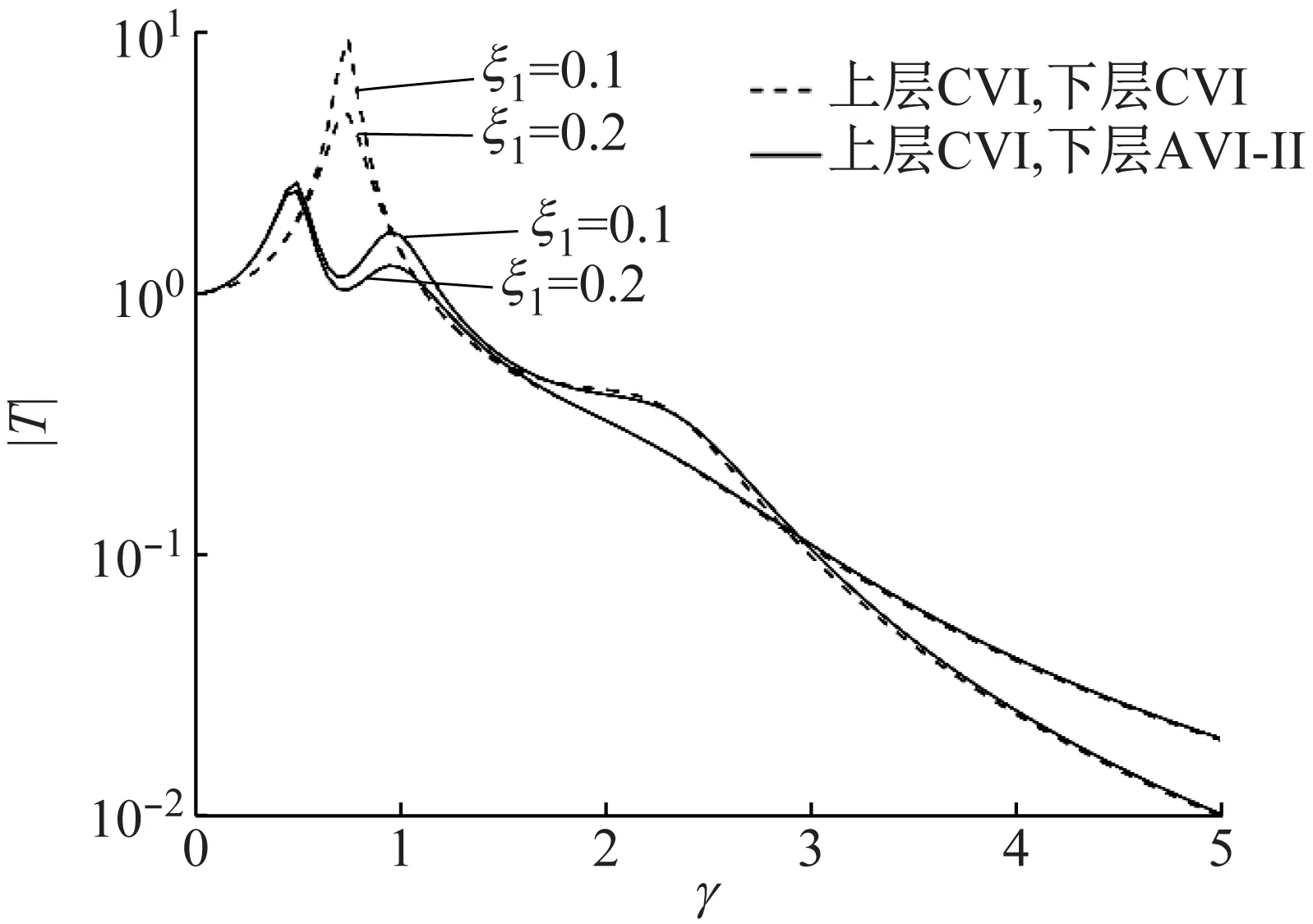
图15 下层反共振隔振时CVI阻尼影响

5 结 论

(1) 在单惯容AVI结构中，二级串联型三元件AVI结构适用于双层隔振系统；与惯容并联的阻尼是全局阻尼，同时控制共振峰值和反共振峰值。

(2) 以AVI-Ⅱ进行双层隔振系统设计，可实现在保持隔振区传递率衰减速率不降低的条件下抑制共振峰值，改善双层隔振性能；在工程可行条件下，宜将AVI-Ⅱ作为下层隔振装置。

(3) 在进行反共振双层隔振系统设计时，可先忽略CVI阻尼，开展AVI-Ⅱ调谐优化，AVI-Ⅱ阻尼按调谐优化值设计，而CVI阻尼应最小化。