基于有限元与能量方法结合的前围板阻尼片布置优化
常光宝,张吉健,罗德洋,白长安
(1.上汽通用五菱汽车股份有限公司技术中心,广西 柳州 545007;2.武汉融声奇科技有限公司,武汉 430014;3.西安交通大学 机械工程学院,西安 710049)
0 引言
阻尼片在汽车行业使用广泛,这些阻尼材料通常由一些柔性材料制作而成(如合成橡胶、橡胶、软木、高密度泡沫和层压材料),被贴装在板件上,用以减小车身板件的振动。正因为这样,阻尼片能够改善金属薄板的隔声效果。优化这些布放位置不仅能够增强隔声效果,还能契合成本控制、轻量化的发展需求。
数值计算已经成为除理论分析和实验测试外的常用研究方式[1],通过有限元的数值计算方法研究结构隔声特性建立在经典力学基础之上,主要包括有限元法和边界元法等。王智文[2]、张若平[3]等对汽车地板阻尼材料与车内振动噪声性能的联系进行了研究,并对车身结构的模态应变能进行分析,优化阻尼,提高NVH性能。赵建轩[4]、郑玲[5]等进一步结合壁板贡献量,降低振动噪声。梅胜军等[6]将模态应变能、壁板贡献量和模态贡献量综合考虑优化阻尼。张一麟等[7]通过观察车身模态并结合壁板贡献度的方法优化阻尼。除了上述的有限元建模外,统计能量方法也是常用的数值计算方法[8],刘春蕾等[9]将60 km/h匀速行驶工况作为计算工况,对司机耳旁声压级进行预测,验证了统计能量分析方法预测噪声的有效性。统计性方法建立在统计力学基础之上,其主要代表有统计能量法等。黄鼎友等[10]利用统计能量法对前围板的隔声性能进行了预测,并与实验测试的结果进行了对比,两者趋势基本一致。但是统计能量法基于统计思想,很难考虑模型细节的影响,因此在计算精度方面有着天然的劣势,主要用于趋势的预测。
在统计能量分析中,模型分子系统或者分块的概念成为近年来的分析热点。相对于单纯的基于网格的有限元方法,分块方法可把若干网格组合成一块,这样整个系统分为若干块,相对于原始网格来说,分块的自由度会降低很多,分析效率会提升很多。基于能量处理的方法可以创建更紧凑的能量模型[11-14],这种方法基于模态,并可以自动将结构划分成多块,分别对每一块计算整体的分布矩阵。这种方法将原来的有限元模型缩减到对每一块的计算上,可以快速地进行指定载荷下的能量评估。
本文采用有限元模型和能量后处理相结合的方法,通过建立更精简的能量模型描述结构部件的动力学响应,并通过编程的方式实现自动计算每个单元块对阻尼的敏感性响应结果。这种方法基于现有的结构模态和刚度质量矩阵,模型中的各结构部件自动划分成很多单元片,并且每个单元片上进行“分布矩阵”组装。该方法可以大幅降低模型计算量,有效提高数值计算效率;同时基于其高效性,可以把该方法集成到优化工作流程中。
1 理论介绍
有限元方法与能量分析方法结合的流程中,基于结构动力学的有限元方法不赘述。能量分析方法是基于有限元结构模态与模型的刚度-质量矩阵(K_M矩阵)来进行分块处理和能量分析,该过程称为能量后处理过程[15]。
能量后处理过程中,首先将有限元模型分解成一系列单元集合(Patch,下文称“单元块”)。每一个单元块是一系列属于相同有限元模型部件的连续的单元集合,且假设在每一个单元块上能量级均匀分布。因此,单元块是这种能量后处理方法的基本构成。图1展示了自动划分的某示意板件的单元块,每个小单元块里面有若干有限元单元网格。
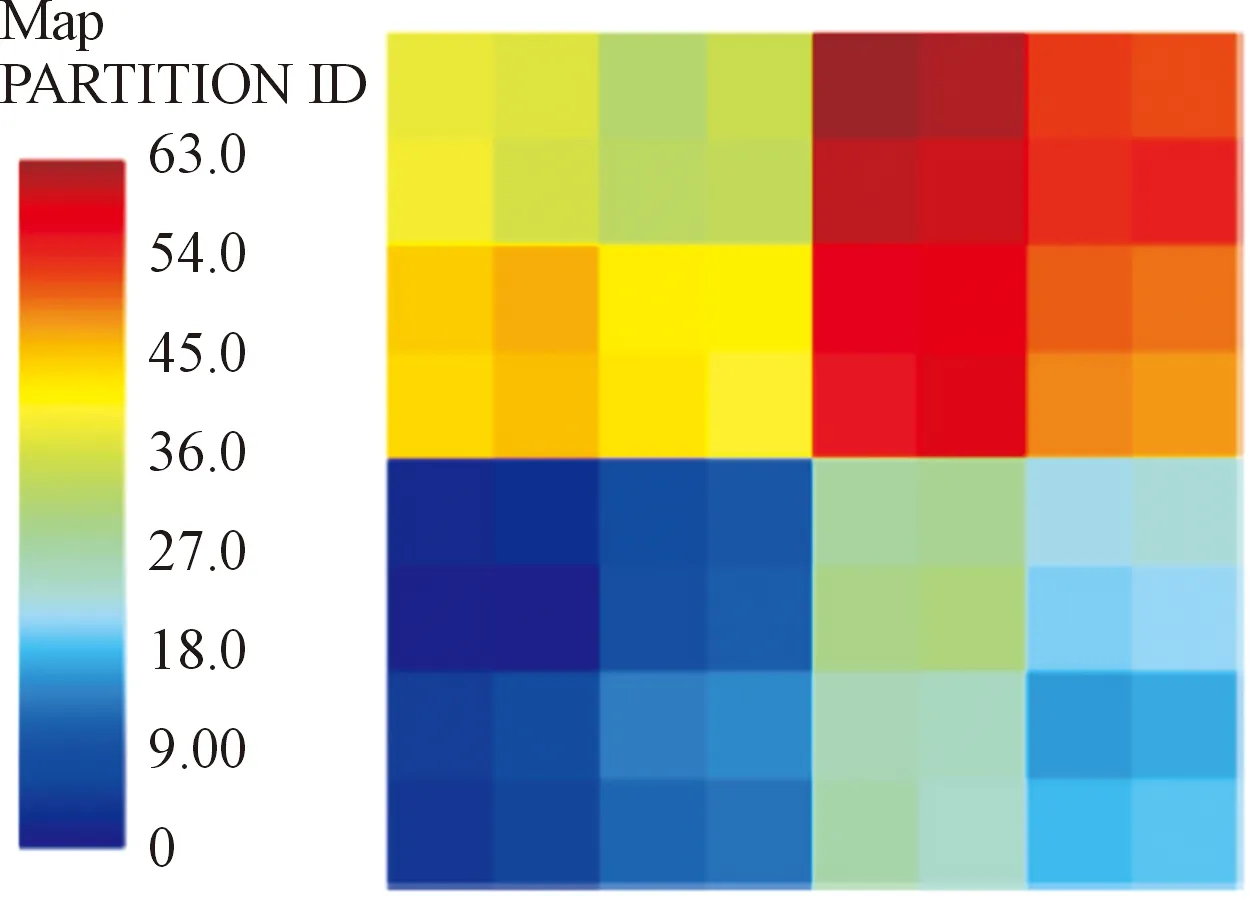
图1 单元块自动划分示意图

(1)
式中:Ki、Mi和Kip、Mip分别为模态坐标系和物理坐标系下的第i个单元块上的刚度阵和质量阵。分布式矩阵Ki和Mi只需计算1次,后续各种载荷作用下的响应计算均调用。
计算单元块的分布式矩阵优势在于可以在单元块的子结构上快速地进行能量计算。也就是说,在各种载荷工况下都可以计算出第i个单元片的动能、势能和耗散功率:
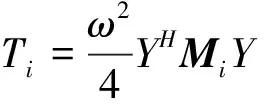
(2)
(3)
(4)
式中:Y为模态坐标位移,Ti、Vi、Wi分别为单元的动能、势能和耗散功率,ηi为阻尼损耗因子,ω为圆频率。
当只有迟滞阻尼决定阻尼片的能量耗散时,可以通过阻尼损耗因子ηi来定义第i个单元块上的阻尼。在每个单元块上定义不同的阻尼因子,就会形成不均匀的阻尼分布。经过循环计算后,可以计算得到哪些单元块对阻尼片较为敏感。
板件的隔声特性仿真分析通常需要用扩散声场作为载荷来模拟无规入射的声能量。扩散声场可以通过多个采样的不相关的、在空间中沿着任意方向传播的平面波叠加获得,可以用来模拟一个弱稳态随机过程,描述这一理论模型的解析表达式如下:
(5)
(6)
式中:k为波数,c为声速,d为声场中2个观察点之间的距离。
2 技术路线
采用数值分析软件与自编程序相结合的方式进行前围板阻尼片位置优化方法研究,研究对象为含钣金件和复合层的前围板结构,其中板件的有限元模型已经确定,采用基于有限元方法与能量方法的敏感性分析流程确定阻尼片的布置位置,技术路线如图2所示。
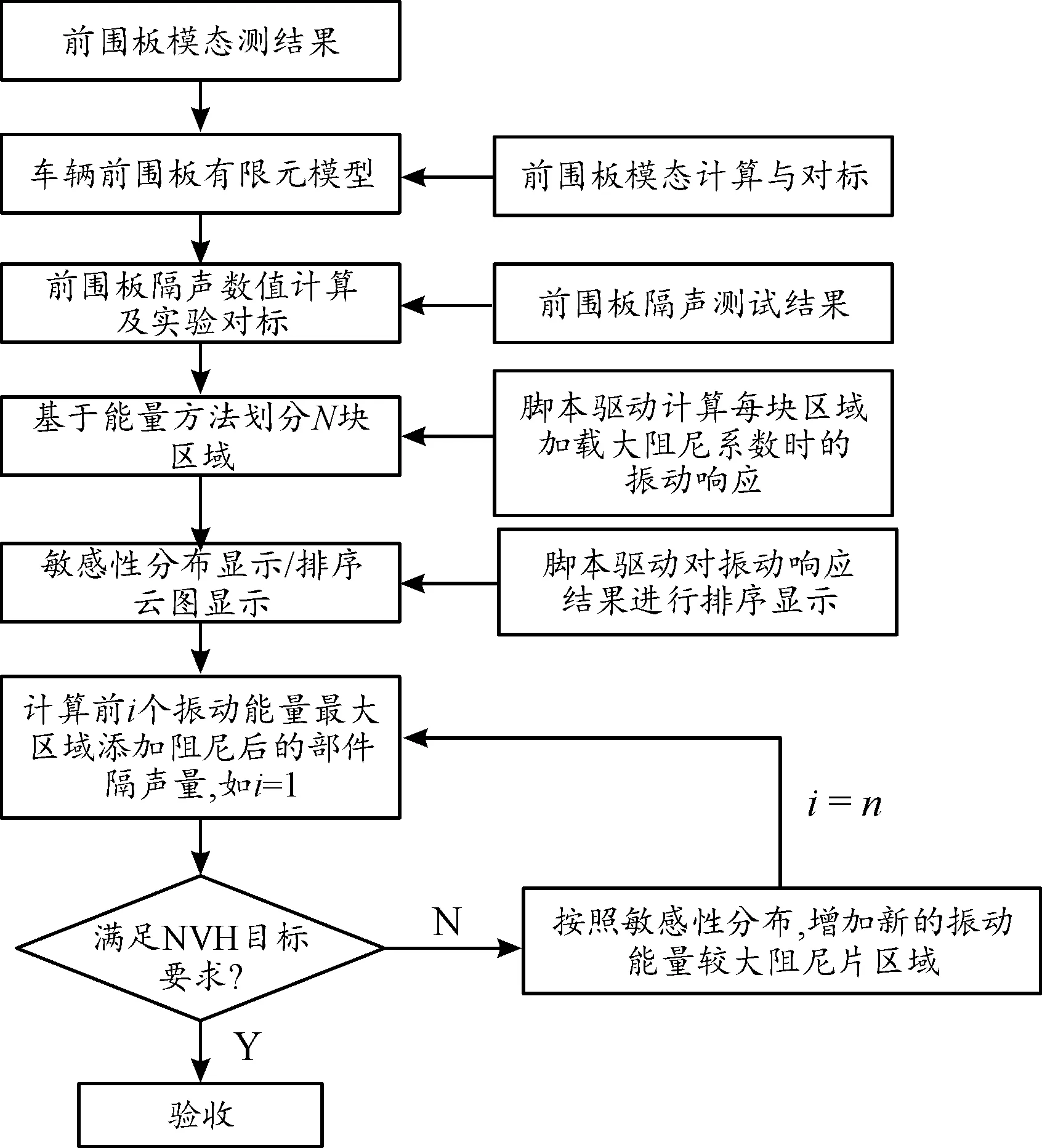
图2 技术路线框图
具体实施所用方法和内容如下所示:
1)在有限元分析软件Nastran中,采用有限元分析的方法进行车辆前围板的有限元模态分析;
2)在声学分析软件Actran中,采用能量分析方法建立能量分析模型,在输入模态结果和刚度质量矩阵(KM矩阵)数据后,设定N个有限元网格组成一个单元块子系统。分析模型中考虑扩散声场激励加载到结构模态上,扩散声场采用25个抽样样本构成随机的分布式载荷激励;
3)使用Python语言编写板件不同单元块对阻尼的敏感性分析程序。因为结构阻尼被认为在各个单元块上是相同的,优化流程最终会得到在各个单元块上阻尼材料的分布量。通过监测扩散声场载荷下的板的法向均方速度来判定板件不同区域对阻尼的敏感性;找到n个阻尼片的最优分布方案:
① 对于每一个单元块,应用一个局部阻尼值;
② 计算对于每一种阻尼材料分布方案的整个板件法向速度的均方值;
③ 每一步都进行针对待优化板件的白车身有限元模型的能量后处理。使用分布矩阵计算每一种阻尼优化方案的残余矩阵。
4)挑选出n个单元块的法向振动速度均方值最小的位置添加阻尼。
在采用传统直接频响法进行每一步计算时,模型自由度由单元数量决定。而能量后处理法中,模型自由度由单元块数量决定。文中优化流程的每一步计算在采用能量后处理方法时,计算模型的自由度都被降低到最少,计算效率更高。在最终验证计算时,采用直接频响法,以确保优化结果的准确性。
3 前围板隔声量性能研究及声学优化案例
3.1 前围板隔声量性能分析
前围板隔声量计算流程如图3所示。隔声量分析模型中,定义前围板结构各部分材料参数,并导入一侧声空间模型,定义为空气材料属性;模型中通过定义耦合面的方式把结构模型和空腔模型耦合起来,保证信息可以正常传递。模型中定义扩散声场激励加载到结构模型上,扩散声场采用25个抽样样本构成随机的分布式载荷激励。
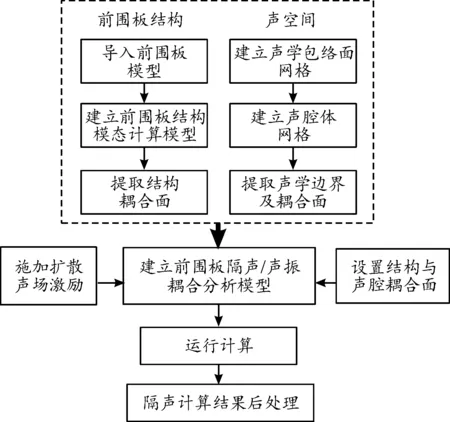
图3 前围板隔声量计算流程框图
隔声量计算模型中,前围板结构有限元模型与声空间有限元模型组合成前围板隔声量计算声振耦合分析模型,模型组成示意图如图4所示。
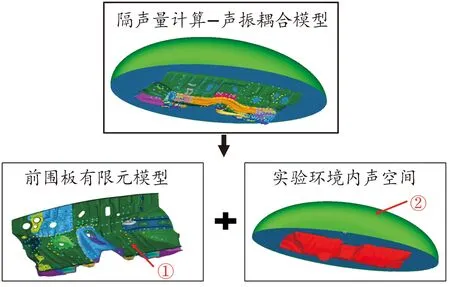
图4 隔声量计算-声振耦合模型组成示意图
图4中,①为扩散声场激励,模拟无规律入射声场激励;②为APML边界,模拟无反射的声场边界。前围板钣金件和阻尼材料参数如表1所示,阻尼材料的阻尼随频率变化。
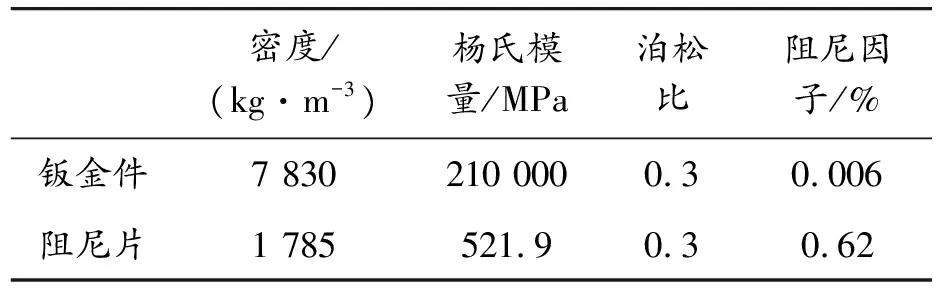
表1 材料参数
隔声量计算完毕,得到隔声量曲线,为了验证仿真计算精度和方法的有效性,取相同模型的实际样件做隔声量测试。前围板隔声测试试验在同济大学声学研究所进行,测试方法按照GB/T 19889.10—2006小建筑构件空气声隔声的实验室测试方法进行,隔声室由两间相邻的混响室组成,如图5所示。试验过程中前围板试验件装置在公共隔墙的开口上,测试温度为16 ℃,相对湿度为80%。试验采用B&K公司的PULSE 3560C作为声源的信号发生器及数采系统,激励信号为白噪声信号。

图5 前围板隔声量测试实验示意图
通过3次测试获得的带阻尼片前围板模型的隔声量数据如图6中红色实线所示;图中蓝色虚线为采用专业声学软件计算得到的带阻尼片前围板模型的隔声量数值模拟数据。
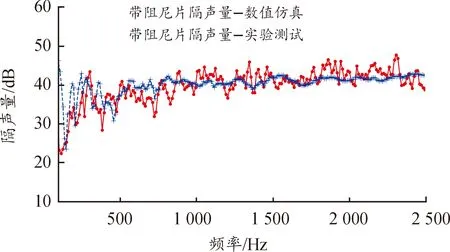
图6 带阻尼片前围板隔声仿真与测试结果曲线
从图6中对比情况来看,两者曲线走向趋势一致,吻合度较高,其中在80 Hz以下频段,隔声计算值与试验值差距较大,这是由于低频一般受边界条件影响较大,而在仿真模型中难以施加与试验状态完全一致的边界条件;在80~2 500 Hz,隔声计算值与试验结果趋势基本一致,计算模型满足工程计算的要求。曲线均在100 Hz处(曲线起始频率)隔声量最小,符合经典板件隔声量曲线中结构共振区隔声量最低的趋势,100~350 Hz为隔声量增大区域。350~450 Hz隔声量逐渐降低,达到吻合频率区,该区间内入射声波的波长在壁板上的投影与壁板中弯曲波的波长相近或相等时,发生吻合效应。450 Hz之后的隔声量曲线呈现逐渐增大的趋势,且实验与数值仿真吻合度较高。计算模型实现了2 500 Hz以内频段的隔声效果,为阻尼片在地板高频段的NVH性能表现提供了预测手段。
3.2 基于能量后处理的阻尼敏感性分析
前围板隔声量计算模型搭建完成且完成隔声量对标后,在后续敏感性分析和位置优化中作为初始输入的基准模型。在声学分析软件Actran中,采用能量分析方法建立能量分析模型,分析模型基于3.1章节隔声量计算模型,在输入模态结果和刚度质量矩阵(KM矩阵)数据后,设定N个有限元网格组成一个单元块子系统。其中前围板结构模态结果如图7所示,图中展示前6阶结构模态的模态位移振型云图。

图7 前围板结构有限元模态位移振型云图(前六阶模态振型)
其中,第一、二、五阶显示局部模态振型;第三、四、六阶显示前围板板件整体模态振型。在做能量分析时,可以设定N个有限元网格为一个单元块,若有限元网格数为S个,最终可以生成的单元块数即S/N个。前围板模型中,有限元网格数为20 945个,如每个单元块包含800个有限元网格,则最终生成25个单元块;为了测试该方法的可靠性,研究了每个单元块中包含200个有限元网格、400个有限元网格、800个有限元网格,共3种计算模型。加载扩散声场激励后,完成能量分析模型。在Python运行程序里设定阻尼循环加载脚本,最终获得每个单元块上的平均振速结果,生成每个单元块对阻尼的敏感性云图,如图8所示。
图8的计算结果中,(a)(b)(c)中左侧图片为安装不同分组方式形成的不同网格数的单元块数的分布图,其中,(a)中每块单元块的网格数最少,所以单元块数最多,(b)次之,(c)中单元块数最少。3个分组图中,右侧图片为加载扩散声场激励后获得的敏感性分析云图,图中颜色代表每块单元块上加载大阻尼系数时整个板件的法向均方振动速度,蓝色表示加载到该区域单元块后,整个板件的振动较小;同理,红色区域表示该区域加阻尼系数后整个板件的振动较大。
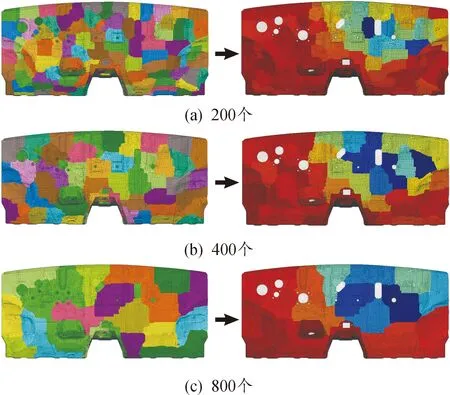
图8 有限元不同分块形式云图
最终在方案选型阶段粘贴阻尼片时,应主要粘贴在蓝色区域,同上考虑到阻尼片质量和工艺加工的要求,从蓝色区域逐次过渡到浅蓝色、绿色区域、褐色区域、浅红区域,最后再选择深红区域。从图8的3种分块方案来看,结果稳定性较好,均在右上区域呈现蓝色且围绕中间孔洞圆周分布,趋势线较为一致。考虑到分块越少,计算效率越高,后续分析时,采用图8(c)方案即可。
3.3 基于敏感性分析的局部阻尼片优化
乘员舱内含大量隔吸声材料,且吸声材料在中高频段的降噪效果更为明显,改进空间较大;相对而言,在中低频范围内的隔声性能,特别是如何提升100~500 Hz的隔声量特性尤为关键。本案例中前围板上原始阻尼片厚度均为0.002 m,总质量为0.85 kg,设定阻尼片增质不超过15%,优化阻尼片位置及其厚度。位置优化依托敏感性分析结果,从蓝色区域开始,选取的区域内按原始厚度0.002 m,其总质量满足原始阻尼片约90%的质量0.78 kg,并把此作为后续阻尼厚度优化的初始模型。
在阻尼厚度优化时,调用声学软件中自带的NLOPT优化算法,以阻尼片厚度为优化变量,以隔声量的平均值为优化目标,迭代20次,计算得到隔声量最大的阻尼厚度方案。图9为迭代后模型与原始模型的隔声量曲线。

图9 阻尼片厚度优化前后隔声量曲线
图9中,蓝色虚线为初始模型隔声量曲线,红色实线为迭代优化后模型的隔声量曲线;2条曲线整体走势一致,优化后模型在140~190 Hz隔声量优于原始模型隔声量。在几个特征峰值频率处,如190、230、250、340和350 Hz等频率处,优化后模型隔声量优于原始模型隔声量,验证了该方法对于优化阻尼片敷设方案的可行性,同时说明了合理的阻尼片敷设方案对于提升隔声量的重要性。
4 结论
1)基于现有结构模态和刚度质量矩阵的能量分析模型,在每个单元块上进行“分布矩阵”组装,并针对具体工况载荷进行计算,将板件结构进行分块处理,并通过脚本实现在每一块板件施加阻尼的计算方式,找到板件对阻尼最敏感的位置。在敏感区域通过自动厚度优化计算,找到各区域最合适的厚度,能够有效地降低阻尼材料的使用量,减重降本。
2)借助声学软件基于Python语言的脚本开发,调用能量后处理方法,对阻尼片有限元建模和实现优化功能。仅需要已有的有限元结构模型作为输入,不需要额外的计算,可非常方便地融入工业设计流程。
3)对于车辆整车阻尼片优化布置,可基于整车结构模态和结构刚度质量矩阵形成能量分析模型,快速获得阻尼敏感性分析结果,且由于考虑真实工况激励如路噪轴头力等,可以快速获得基于真实激励的整车阻尼优化布置方案。对汽车钣金件类零件的前期设计有较好的指导意义。

