面向NVH性能的汽车冷却风扇拓扑结构设计

杨 丽，李奕慈，刘杰昌，黄元毅，陈翔靖

(1.上汽通用五菱汽车股份有限公司，广西 柳州 545007；2.湖南大学 机械与运载工程学院，长沙 410082)

0 引言

轮胎噪音、车身气流噪音与发动机舱噪音是影响汽车室内噪声的主要噪声源[1]。汽车冷却风扇噪声属于发动机舱噪声，是发动机舱的主要噪声源之一，通过降低冷却风扇的噪声可以降低发动机舱噪声，从而提高汽车的振动噪声性能。冷却风扇噪声可分为2种形式：一种是风扇页片转动时扰动气流发出的风噪声；另一种是风扇电机振动传递至车身，使车身钣金振动发出结构噪声。

近年来，国内外许多学者对降低汽车冷却风扇噪声开展了相关的研究。Zhong等[2]采用多目标优化方法对汽车冷却风扇的叶片结构进行优化分析，减小了汽车风扇的噪声。Andrea等[3]分析和对比了不同叶间距变化规律下风扇的噪声值，通过优化设计提出了非均匀叶间距有利于降噪的结论。王涵松等[4]通过设计一种车用冷却风扇的主动降噪装置来降低汽车冷却风扇的噪声。段传学等[5]通过对风扇叶片进行多目标优化得到了高效低噪声风扇并进行了实验验证。彭志刚等[6]提出了一种动-静叶片相位调制的方法，从整体上降低了汽车冷却风扇组件的离散噪声水平。然而，目前对冷却风扇噪声的研究多集中在风扇结构对噪声的影响，很少有人研究风扇的结构优化，以及不同的材料对风扇噪声的影响。

本文提出了一种新的设计方法，即基于玻璃纤维复合材料，对玻璃纤维的体积分数进行选择，应用有限元仿真分析及拓扑优化方法对冷却风扇的结构进行优化，通过替换风扇的材料和优化风扇的结构来降低冷却风扇的振动，从而降低汽车噪声，达到提高汽车NVH性能的目标。

1 冷却风扇振动和噪声问题分析

在某车型的开发中，怠速噪声比竞争车型大 3 dB左右，而且在43 Hz处的噪声要远远大于标杆车型，如图1所示。针对该型汽车在怠速时的噪声和振动进行了测试，如图2所示。图2(a)为该型汽车怠速时驾驶员右耳处声压测试曲线；图2(b)为冷却风扇电机的振动测试曲线，其中43 Hz峰值频率与风扇电机额定转速对应，由经验可初步判断该峰值是由冷却器风扇振动引起的结构噪声。

图1 汽车怠速噪声曲线

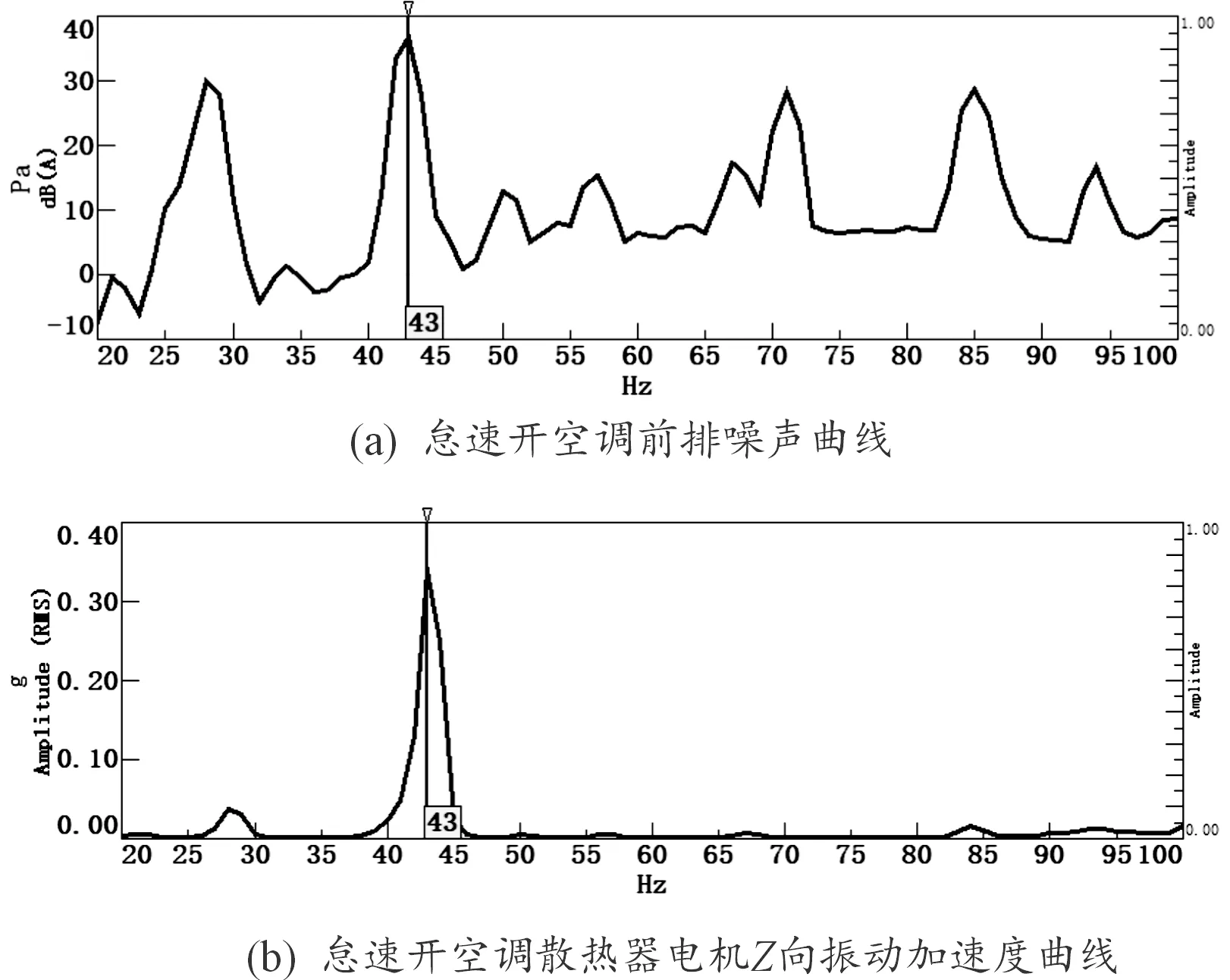
图2 汽车怠速噪声及振动测试曲线

冷却风扇振动的激励来源通常有2种：一种是电机电磁场引起的电磁激励，其频率与电机线圈绕组数量成正比；另一种是电机转动时其动不平衡引起的偏心激励，如图3所示。偏心激励频率计算公式如下：

图3 电机动不平衡示意图

f=w/60

(1)

式中：f为电机偏心激励频率，w为电机额定转速。本研究风扇电机额定转速为2 580 r/min，由式(1)可求得电机偏心激励频率为43 Hz，与图2中冷却器风扇电机振动加速度峰值相吻合，以此可推断偏心激励即为电机振动的激励来源。

电机动不平衡是由材料密度的不均匀性、零件外形加工误差及装配误差等多种因素导致通过电机转子质心的惯性轴偏离旋转轴引起的[7-8]。因此，若试图减小电机动不平衡不但技术困难且会大大增加制造成本。

风扇电机振动可看作是强迫振动系统，其振动能量与激励的关系为：

Wf=πBP0sinφ

(2)

B=P0/Kd

(3)

式中:Wf为激励对系统做的功，B为振幅，P0为电机激励，φ为激励与位移的相位差，Kd为激振点动刚度。

由式(2)可看出，激励对系统做的功Wf与振幅B及激励大小P0成正比，由于激励大小P0很难改变，因此可以通过减小振幅B来减少激励对系统做的功。由式(3)可知，激振点动刚度Kd与振幅B成反比，增大动刚度Kd可以达到减小振幅B与激励对系统做的功Wf的目的。

为了验证推测的结果，对风扇中心的动刚度进行研究，如图4所示为汽车冷却风扇。根据风扇CAD模型建立风扇罩有限元模型，风扇罩结构基本属于薄壁结构，厚度上的尺寸要比其他方向小很多，故在本文中采用基本尺寸为10 mm的四边形壳单元，并对关键部位进行局部细化。整个风扇罩以四边形单元为主，也存在部分用于过渡的三角形单元。此外，考虑到模型的计算时间和精度的平衡，将最小单元尺寸设置为大于3 mm。对风扇罩施加相应的工作工况，在风扇安装处施加约束，在风扇质心处加载Y向与Z向单位激励，如图5所示。最后，把设置好工况的有限元模型提交到Optistruct中计算风扇罩的动刚度。

图4 汽车冷却风扇结构示意图

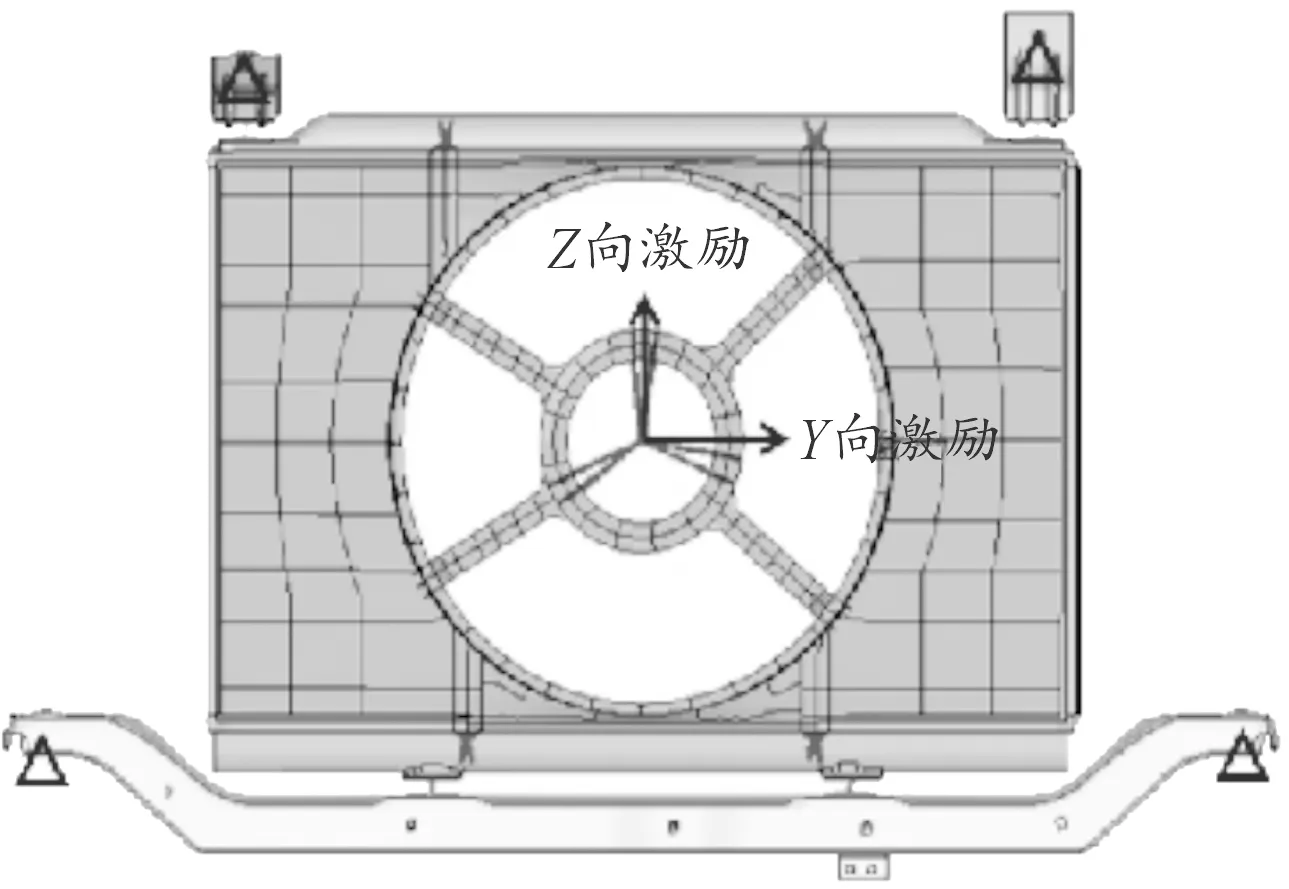
图5 风扇有限元模型示意图

如图6为运用有限元方法计算得到的风扇电机转子中心动刚度仿真曲线。其中Z向动刚度在41 Hz存在极小值，与风扇额定转速频率43 Hz极为接近，极易导致共振从而起到放大振动的负作用。因此，需要对风扇结构进行优化，提高43 Hz附近动刚度。为了实现风扇成本、性能的均衡设计，对玻璃纤维复合材料的体积分数进行选择，并采用拓扑优化的方法实现风扇结构的优化，从而提升振动噪声性能。

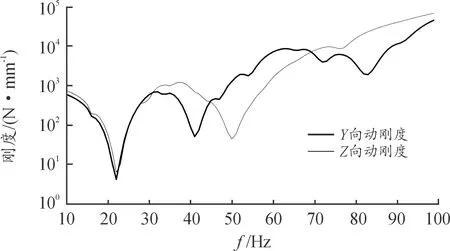
图6 风扇电机转子中心动刚度仿真曲线

2 玻璃纤维复合材料微观参数的设计

玻璃纤维复合材料指以玻璃纤维及其制品为增强材料和基体材料，通过一定的成型工艺复合而成的一种材料[9]。玻璃纤维复合材料具有良好的耐热性、耐腐蚀性，不导电、抗拉强度大，非常适合应用到汽车零部件中[10]。为了寻找玻璃纤维复合材料性能与成本的平衡点，采用均匀化方法对玻璃纤维复合材料的性能进行预测。

2.1 均匀化理论

均匀化方法是一种通过周期性均质材料来代替非均质复合材料[11]，并通过适当的方法求解非均质复合材料的等效弹性模量的方法。假设两相复合材料的代表体积单元(RVE)为，v0为基体相ω的体积分数，则增强相ω1的体积分数为1-v0，有：

(4)

式中：f为RVE中的微场，可以通过对微观坐标x积分求得。此外，可以得到如下关系：

(5)

当边界条件为线性位移时，宏观结构的应变与组分的平均应变〈ε〉ωi之间有如下关系：

〈ε〉ω1=T∶〈ε〉ω0

〈ε〉ω0=[v1T+(1-v1)I]-1∶〈ε〉

〈ε〉ω1=T∶[v1T+(1-v1)I]-1∶〈ε〉

(6)

式中：T为应变浓度张量，其中I表示4阶对称单位张量。因此，复合材料的等效刚度矩阵可以表示为：

〈K〉=[v1K1∶T+(1-v1)K0]∶[v1T+(1-v1)I]-1

(7)

式中：K1为增强相的平均刚度，K0为基体相的平均刚度。

2.2 均匀化方法预测复合材料性能

为了预测玻璃纤维复合材料的性能，结合复合材料的微观结构具有不均匀性的特点[12]，通过建立一个RVE模型来实现复合材料微观尺度和宏观尺度之间的转变，且RVE模型可以完整地体现复合材料微观结构中的纤维取向和体积分数。RVE模型的好坏会直接影响到预测结果的精度，本文运用Digimat建立玻璃纤维复合材料的RVE模型来研究其宏观性能，RVE模型如图7所示，其中(a)(b)(c)分别代表玻璃纤维体积分数为20%、30%、40%时的复合材料的RVE模型，其中红色部分代表玻璃纤维增强体，透明部分代表基质，纤维的取向设置为Random 2D，即在二维平面内绝对随机分布，以保证建立的RVE模型与实际制造出来的复合材料保持高度的一致，纤维的长径比为5保持不变。最后，对RVE模型施加工况，即在RVE边界上施加单轴拉伸应变，初始应变为0，峰值应变为0.04，提交计算并可视化结果。

图7 不同玻璃纤维体积分数的复合材料的RVE模型

不同玻璃纤维体积分数的复合材料应力-应变曲线如图8。

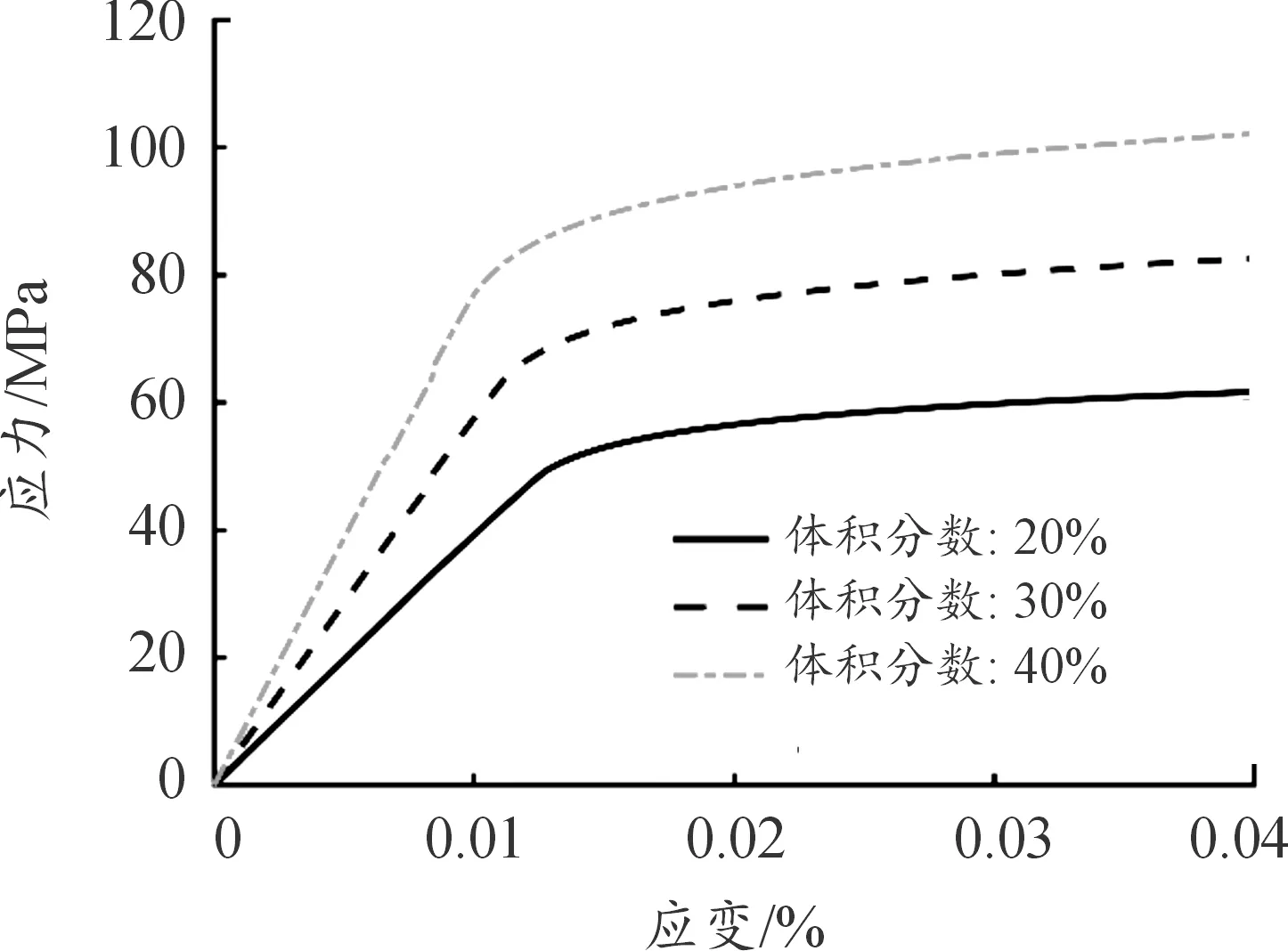
图8 不同玻璃纤维体积分数的复合材料应力-应变曲线

由图8可知，玻璃纤维复合材料的性能虽然低于钢材的性能，但玻璃纤维的质量较小，是非常理想的轻量化材料，故可以在对强度要求不高的汽车零部件上使用。从图8可以看出，玻璃纤维复合材料的弹性模量(图8中曲线弹性阶段的斜率)随着玻璃纤维体积分数的增大而增大，其性能也随之提高。然而玻璃纤维体积分数越高，复合材料的制造成本也越高，因此，需要在性能和成本之间找到一个平衡点，以达到最优的性价比。综合考虑性能和成本，选取玻璃纤维体积分数为30%的复合材料作为替代材料进行研究。

3 基于玻璃纤维复合材料的风扇结构优化

由图4所示汽车冷却风扇结构图可以看出，支撑电机的4根辐条是风扇结构中最为薄弱的地方，也是提高扇页中心动刚度的关键所在。为了提高冷却风扇的动刚度，用玻璃纤维复合材料代替原材料，并对辐条结构进行拓扑优化以达到结构最优的效果。

3.1 拓扑优化理论基础

3.1.1平衡方程及材料插值方案

当物体受外部激励作用时，其振动方程可以表示为：

(8)

式中：M为质量矩阵，K为刚度矩阵，Ft为外部激励。当角频率ωt给定时，Ft可以表示为：

Ft=Fejωtt

(9)

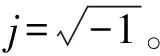
Ut=Uejωtt

(10)

(11)

式中：U为位移响应的幅度。把式(9)-(11)代入式(8)可得给定角频率下对应的结构平衡方程：

(12)

为了减少动态情况下的局部振动，采用如下材料插值方案：

ρ(xe)=xeρ0

(13)

(14)

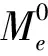
(15)

(16)

3.1.2拓扑优化问题

拓扑优化主要采用变密度法，即将有限元模型设计变量的每个单元的“密度”作为设计变量[13]，其数学模型为：

(17)

式中：γ为目标函数，U为结构位移响应，xe为第e个设计变量，Ne为设计变量的数量，xmin和1为代表单元密度，χ、V0和Ve分别为约束体积分数、设计域体积分数及离散单元体积。

3.1.3灵敏度分析

灵敏度为目标函数对设计变量的偏导[14]，表示如下：

(18)

通过引入一个载荷向量L来计算∂Un/∂xe，可以表示为：

(19)

式中：Ln为第n个目标自由度的载荷向量，ns为第n个目标自由度的序列号，nd为自由度数。因此，∂Un/∂xe。可以描述为：

(20)

根据链式法则可从式(12)中得：

(21)

此外，引入伴随向量Λn，表达式如下：

(22)

把式(20)-(22)代入式(18)可得：

(23)

式中，∂K/∂xe和∂M/∂xe可以从式(15)和(16)中计算得到。因此，灵敏度可表示为：

(24)

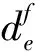
3.2 汽车风扇拓扑优化设计

根据汽车冷却风扇结构CAD模型建立用于结构优化的冷却风扇有限元模型，如图9所示，把风扇结构分为设计域和非设计域，设计域为需要拓扑优化的区域即为风扇的辐条所在的区域，如图9中的拓扑优化变量。冷却风扇拓扑优化的数学模型表示如下：

(25)

式中：M(x)为风扇质量，目标函数为最小化质量；s.t为约束条件；Kz、Ky、Kx分别代表z、y、x3个方向的动刚度；Kz0、Ky0、Kx0分别代表z、y、x3个方向的原始动刚度，x为设计变量，xmin和1为代表单元密度，优化计算后单元密度越大表示该处结构越重要，需要保留；单元密度越小则表示该处结构越不重要，可以去除[15-17]。根据数学模型，设置拓扑优化的参数设置如表1所示。并在模型中设置如图9所示。

表1 风扇结构拓扑优化参数

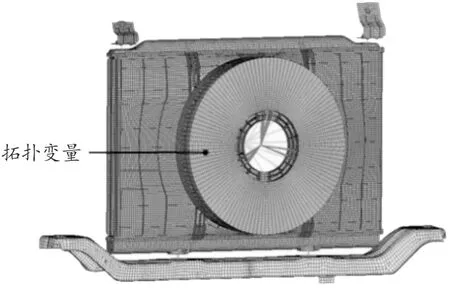
图9 风扇拓扑优化有限元模型示意图

把设置好工况的有限元模型提交到Optistruct进行优化计算，最终得出如图10拓扑形状。

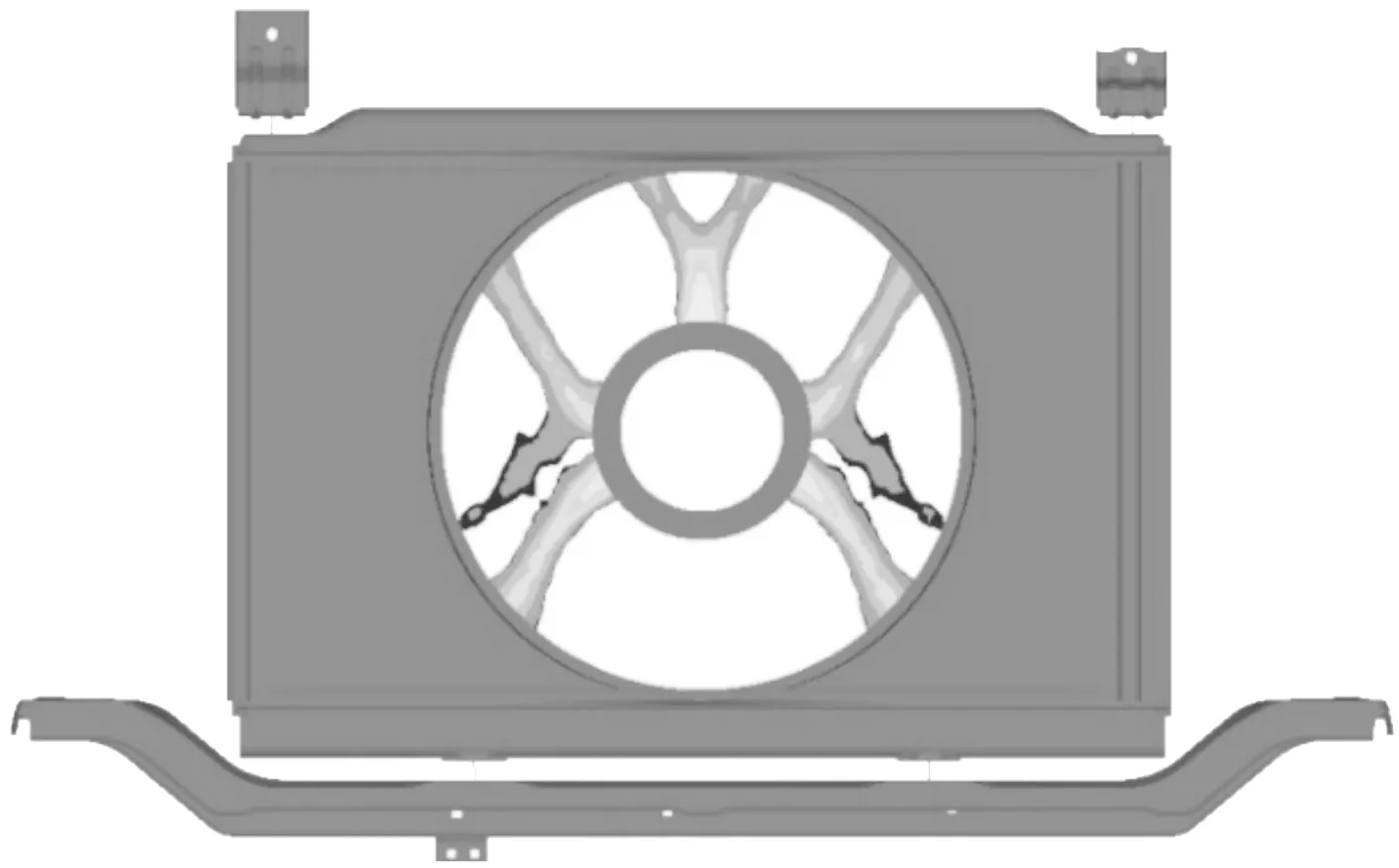
图10 拓扑优化结果示意图

根据图10拓扑概念形态对风扇电机支撑辐条结构进行优化设计，绘制三维CAD模型，如图11所示。根据优化结果建立其有限元模型，并施加与优化前分析模型一致的载荷，如图12所示。

图11 优化方案三维模型示意图

图12 优化后风扇有限元模型示意图

风扇模型的材料分别使用原始材料和玻璃纤维复合材料，并将模型提交到Optistruct进行结构动刚度计算，最后将计算结果与优化前的结构动刚度作图，如图13所示。

图13 优化前后风扇中心Y、Z方向的动刚度曲线

图13为冷却风扇在原始结构及原始材料、优化结构及原始材料、优化结构及玻璃纤维复合材料下风扇中心Y、Z方向的动刚度仿真结果。图13中的原方案代表在冷却风扇原始结构、原始材料下的仿真结果；方案1代表冷却风扇在优化结构、原始材料下的仿真结果；方案2代表冷却风扇在优化结构及使用玻璃纤维复合材料替换了原始材料下的仿真结果。由图13可知，在方案1即只改变风扇结构的情况下，Z方向的动刚度极小值由41 Hz提高至53 Hz，后移了12 Hz，且在41 Hz附近没有产生新的极小值，优化方案使冷却风扇的极小值远离了风扇额定转速频率43 Hz，避免了共振的产生；在方案2即同时改变风扇结构和材料的情况下，冷却风扇的Z向动刚度产生极小值的地方由41 Hz后移到了60 Hz处，提高了19 Hz，有效地避免了与风扇电机的共振的产生，且该优化方案的优化效果明显优于方案1。

表2为汽车冷却风扇优化前后Y向和Z向动刚度。

表2 汽车冷却风扇优化前后Y向和Z向动刚度 N·mm-1

从表2可以看出，在运用原始材料的情况下，冷却风扇优化后的动刚度有了一定的提升；使用玻璃纤维复合材料替换了原始材料后，冷却风扇的Y向和Z向动刚度相对于原始结构都得到了几倍的提升，提升效果非常明显，表明了对冷却风扇材料的替换和对冷却风扇的结构优化设计在提高结构的动刚度上具有非常好的效果。

4 方案实验验证

为了验证仿真优化的结果的可靠性，根据优化结果的三维模型进行样件试制，并安装到整车上验证优化效果，样件如图14所示。将样件安装到该车型上进行怠速噪声测试，测试结果如图15。从图15测试结果中可以看到，相对于原状态的风扇结构，风扇结构优化后的车内噪声在43 Hz频率处下降了12 dBA，改善效果明显；响度下降0.49 sone，有效提升了汽车NVH性能。

图14 试制样件图

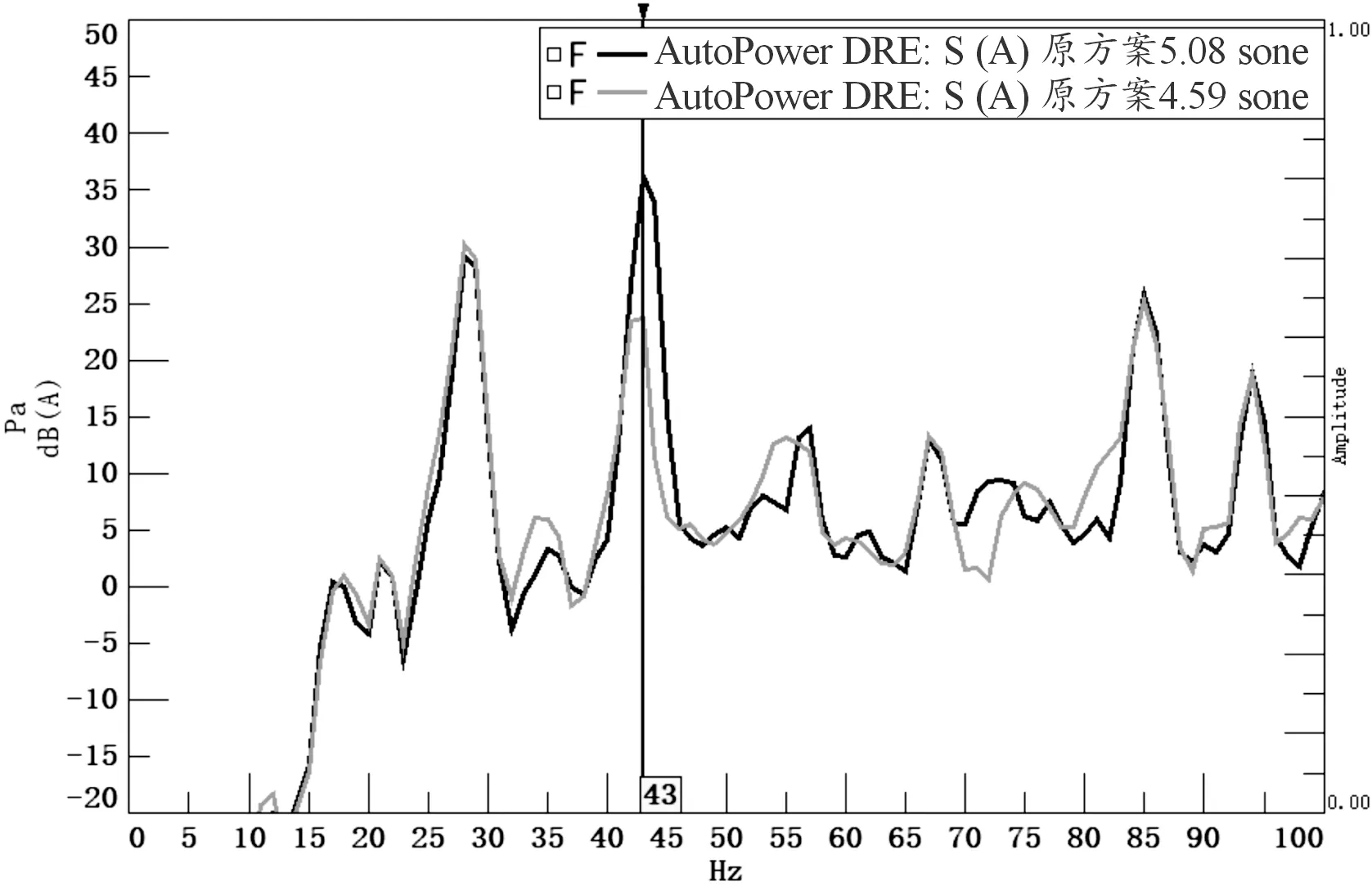
图15 样件测试结果曲线

5 结论

对某型汽车在怠速时的噪声和振动进行测试并确定了噪声来源于汽车冷却风扇，提出了一种基于玻璃纤维复合材料汽车冷却风扇设计优化方法，对玻璃纤维复合材料的体积分数进行优化以实现玻璃纤维复合材料成本、性能的均衡设计；接着应用有限元分析和拓扑优化方法对玻璃纤维复合材料汽车冷却风扇进行设计，同时对比了冷却风扇在结构优化之后使用原材料和玻璃纤维复合材料的性能，结果表明使用玻璃纤维复合材料替换了原始材料后，冷却风扇的结构模态频率和动刚度有了非常大的提升。根据优化方案对冷却风扇进行样件试制，并安装到汽车上进行噪声测试及汽车整车物理实验验证。结果表明，风扇结构优化后噪声下降了12 dBA，响度下降了0.49 sone，优化方案降噪效果明显。