采用HB-AFT方法的多楔带附件驱动系统动态响应计算与分析
李 涛,魏政君,上官文斌,吕 辉
(华南理工大学 机械与汽车工程学院,广州 510641)
0 引言
多楔带传动作为常见的机械传动方式,通过多楔带与带轮之间的摩擦力进行传动,具有结构简单、传动平稳、制造成本低等特点[1]。多楔带附件驱动系统通常是由一个驱动轮,若干个附件轮和惰轮,一个张紧器以及一根多楔带组成[2],如图1所示。当驱动轮的扭转振动传递到该系统中,会引起相关的动态响应,如张紧器的摆动、多楔带的张力波动等[3]。过大的动态响应,会影响系统的平稳传动,并降低多楔带、张紧器等零部件的使用寿命[4]。因此,在设计开发初期,需要检验多楔带附件驱动系统的动态响应情况是否满足使用要求。准确预测系统的动态响应,对该系统的设计开发具有重要的意义。

图1 多楔带附件驱动系统结构示意图
目前已有大量学者对张紧器的建模以及多楔带附件驱动系统动态响应计算方法进行了研究。在张紧器建模方面,Zhao等[5]将自动张紧器内部的摩擦视作干摩擦,摩擦力的大小与方向只与速度方向有关。该模型物理意义明确,表达式简单。Zhu等[6]也将自动张紧器内部的摩擦视为干摩擦,并利用双曲正切函数对其进行连续化,之后展开为傅里叶级数,得到了近似的张紧器模型。Michon等[7]将自动张紧器的输出力矩分解为3部分,即弹性力距、黏性阻尼力矩以及摩擦力矩。在Dahl模型的基础上进行简化,建立了描述自动张紧器迟滞特性的Duhem模型,并推导了Duhem模型中张紧器输出力矩与张紧器摆角的显式表达式。Bastien等[8]则利用修正的Dahl模型和Masing模型描述自动张紧器的迟滞特性。
在多楔带附件驱动系统动态响应计算方法的研究上,目前的计算方法主要分为3类:等效线性化法[3,9-10]、谐波平衡法[6,11]、迭代法[12-13]。将张紧器的摩擦特性简化为库伦干摩擦,用谐波平衡法来求解,其计算精度比等效线性化法高,并可分析张紧器的粘滑运动现象。然而,张紧器的实际特性并不完全等同于库伦干摩擦。为了将更准确的张紧器特性考虑到系统动态计算中,可用迭代方法进行计算,解决张紧器输出扭矩与响应幅值相互依赖的问题,具有很高的计算精度。但是当系统的自由度较大时,需消耗大量的计算时间。
综上所述,为了在保证较高计算精度的同时,又提高计算效率,提出用谐波平衡法-时频域转换技术(HB-AFT)计算多楔带附件驱动系统的动态特性。HB-AFT是一种半解析半数值方法,常被用来求解非线性系统的稳态响应[14-15]。其核心思想是在频域内求解系统微分方程,在时域内求非线性力[16-18]。在计算过程中,通过在时域和频域之间的切换,既可保证计算精度,又可提高计算速度。
以一个三轮多楔带附件驱动系统为研究对象,首先建立其数学模型,并基于HB-AFT方法计算在特定激励下系统的稳态响应情况,在求解过程中考虑了张紧器的非线性迟滞特性。将HB-AFT方法的计算结果与数值积分结果进行比较,验证HB-AFT方法在计算多楔带附件驱动系统稳态响应时具有高精度、高效率的特性。
1 多楔带附件驱动系统的数学模型
1.1 时域数学模型
1.1.1模型假设与简化
以三轮多楔带附件驱动系统为例,在建立三轮多楔带附件驱动系统的数学模型之前,需要先对系统进行一定的简化[10]:
1)多楔带在纵向上的质量分布是均匀的,并且忽略多楔带的蠕变效应;忽略多楔带的弯曲刚度以及纵向拉伸阻尼;忽略多楔带与带轮之间的滑移对系统动态响应的影响,并且不考虑多楔带横向振动对纵向振动的影响。
2)各轮的轴承摩擦等效为黏性阻尼,并认为黏性阻尼系数不会改变。
3)忽略张紧器所受重力的影响。
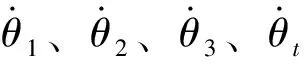
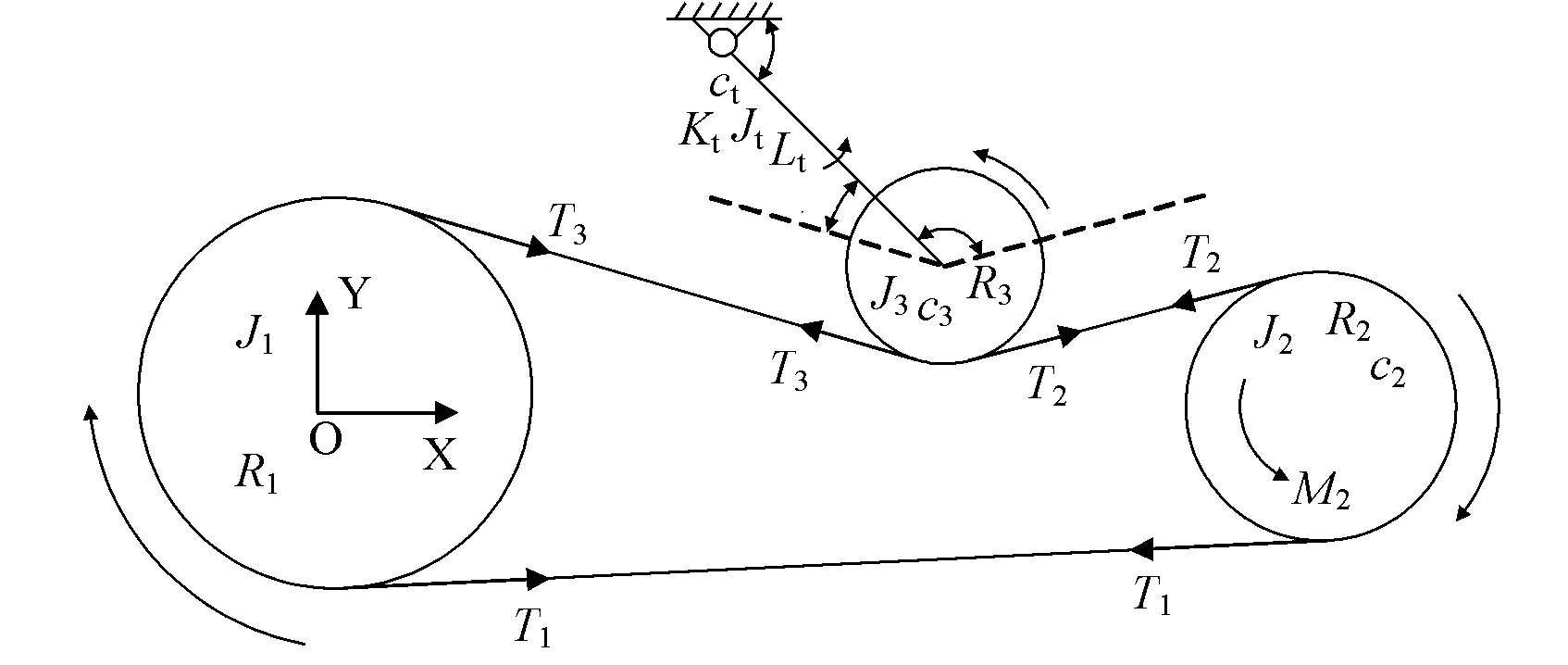
图2 三轮多楔带附件驱动系统示意图
1.1.2系统激励
在稳态工况时,驱动轮的转速往往不是保持不变的,而是在平均转速附近波动,工程上称这种现象为扭振。此时,驱动轮的转角可用下式表示:
(1)
式中:N为驱动轮的平均转速,k为扭振的阶次,Ak(N)代表第k阶扭振的幅值,φk(N)为第k阶扭振的相位,t为驱动轮的工作时间。
驱动轮的扭振会传递到多楔带附件驱动系统中,引起多楔带的张力波动,带轮的转速波动以及张紧器的往复摆动。对于常见的四缸四冲程车用内燃机,2阶扭振是主激励,在常用转速区间其幅值远大于其他阶次扭振的幅值,如图3所示。因此,在本文的计算中只取2阶扭振作为系统的激励,忽略其他阶次的扭振。

图3 四缸四冲程车用内燃机各阶扭振振幅随转速的变化曲线
1.1.3运动方程
Ⅰ 张紧器的模型
如图4(a)所示,利用Masing模型,将张紧器视作由3部分并联组成,分别是黏性阻尼ct、线性弹簧Kt以及由干摩擦副与线性弹簧Kl串联组成的元件[8]。黏性阻尼ct与线性弹簧Kt产生的作用力矩均是线性力矩,而干摩擦副与线性弹簧Kl串联组成的元件产生的作用力矩则是非线性力矩Mt。Mt的非线性特性正是张紧器非线性迟滞特性的来源,Mt与张紧器摆角θt的关系如图4(b)所示。

图4 摩擦式张紧器的Masing模型示意图
在图4(b)中,Mf代表干摩擦副提供的滑动摩擦力矩,θa为张紧臂摆动的平衡位置,θm为张紧臂摆角的幅值,θs为黏滞运动的最大幅值。θs可按照式(2)计算:
(2)
已知张紧臂的摆动角度、摆动方向以及摆角幅值时,非线性力矩Mt的分段表达式如式(3)所示:
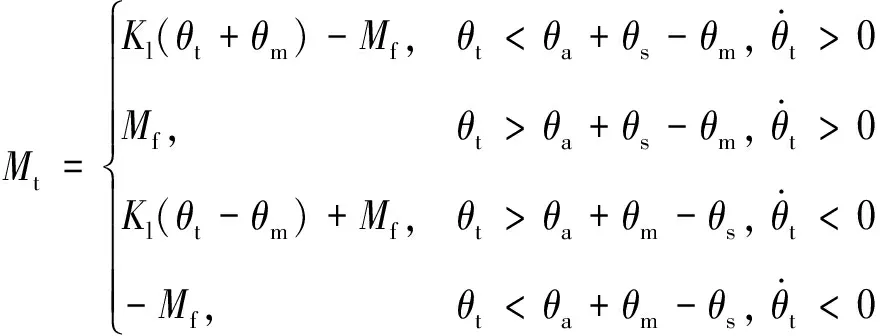
(3)
Ⅱ 张紧臂的运动方程
对于张紧臂,其受力情况如图5所示。张紧器的加载方向为逆时针方向,根据动量矩定理,可以建立张紧臂关于其旋转中心的力矩平衡方程[19]:
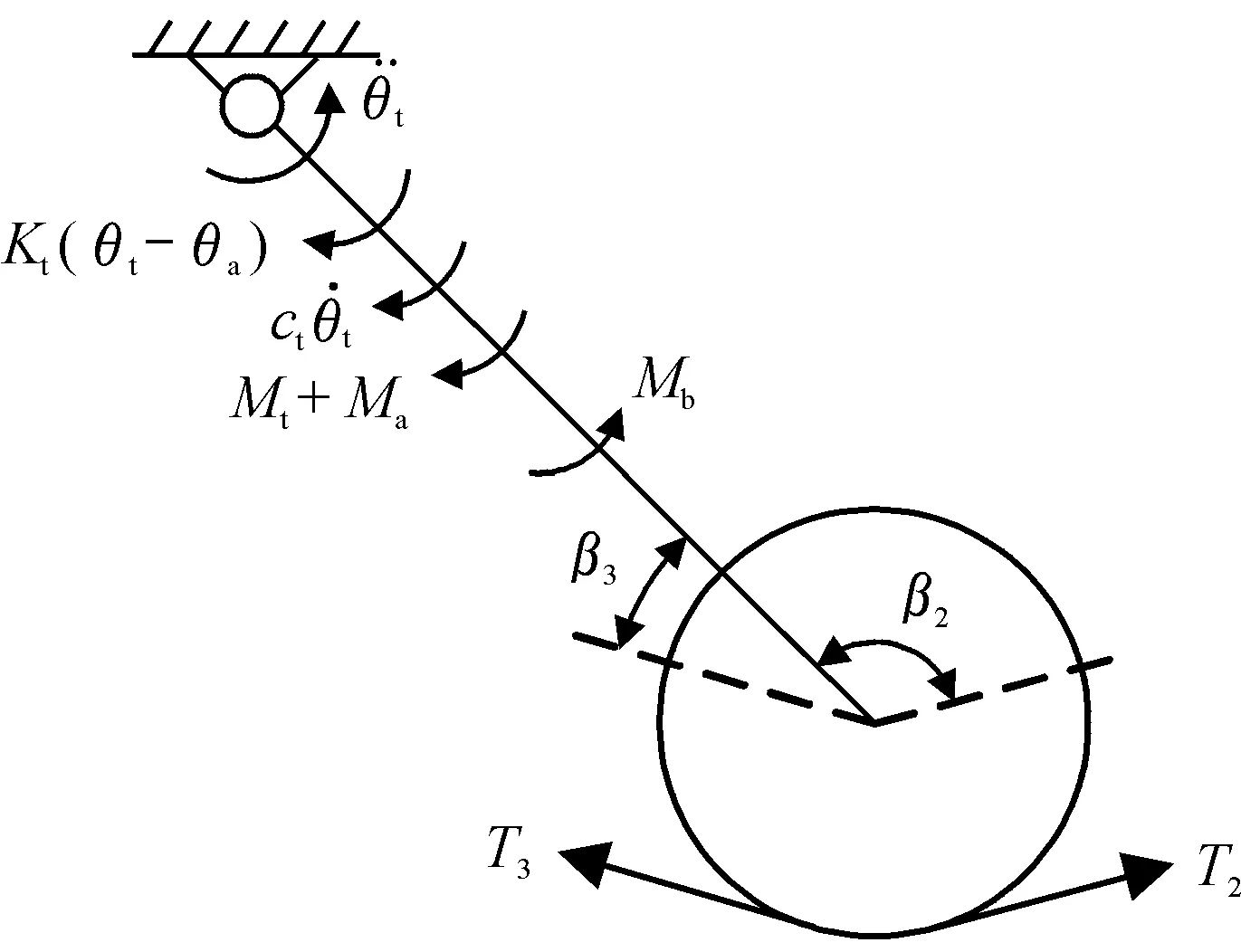
图5 张紧臂的受力情况示意图
(4)
式中:Ma为张紧器在平衡位置时的弹簧预载,Mb为张紧轮两侧带段张力对张紧臂产生的合力矩,其计算方法如下[19]:
Mb=T2Ltsinβ2-T3Ltsinβ3
(5)
Ⅲ 带段张力与带轮的运动方程
带段的张力与带段的伸长量有关系,因此,各个带段的张力可根据式(6)计算[3,10,19]:
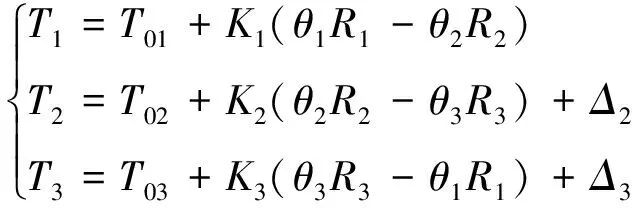
(6)
(7)
式中:T01、T02、T03分别为各带段的初始张力,Ki为带段Bi的纵向刚度,E为杨氏模量,A为横截面积,Δ2和Δ3分别为由于张紧臂摆动引起的带段B2、B3的长度变化,其精确计算方法见文献[3]。
对于带轮i,根据受力平衡关系,其运动方程为[3]:
(8)
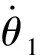
1.1.4几何线性化
式(5)中的β2和β3以及式(6)中的Δ2和Δ3都是关于张紧臂摆角θt的非线性函数,这种非线性关系称为几何非线性。在建立三轮多楔带附件驱动系统的频域数学模型之前,需要进行几何线性化。当张紧臂的摆角较小时,可以在张紧臂摆动的平衡位置附近进行几何线性化[10]。
如图6(a)所示,当张紧臂往加载方向小角度摆动φt时,可以认为张紧轮两侧带段与张紧臂的夹角保持不变,即β2和β3分别保持为β20和β30不变。其中,β20和β30分别为张紧器在平衡位置时张紧轮两侧带段与张紧臂的夹角。张紧臂摆动前后,张紧轮圆心的距离为:
do≈Ltsinφt
(9)
两张紧轮圆心的连线与带段B2的夹角α可通过下式计算得到:
(10)
于是,带段B2的伸长量Δ2为:
Δ2≈-Ltsinφtcosα≈-Ltφtsinβ20
(11)
同理,如图6(b)所示,带轮B3的伸长量Δ3为:
Δ3≈Ltφtsinβ30
(12)
如图6(c)所示,由于假设β2和β3保持不变,则根据式(5)(6)(11)(12)可计算得张紧轮两侧带段张力对张紧臂产生的合力矩为:

图6 几何线性化示意图
Mb≈Lt[T02+K2(θ2R2-θ3R3)-Ltφtsinβ20]sinβ20-
Lt[T03+K3(θ3R3-θ1R1)+Ltφtsinβ30]sinβ30
(13)
经过以上的几何线性化过程,β2、β3、Δ2和Δ3都转化为关于张紧臂摆动的角度φt的线性函数。
1.2 频域数学模型
当驱动轮不存在扭振时,张紧器处于平衡位置。再根据1.1.1中的假设,可得各带轮之间的转角和转速的关系:
(14)

于是,由式(6)得各带段的张力为
T1=T01,T2=T02,T3=T03
(15)
将式(14)(15)代入式(8)可得

(16)
当驱动轮存在扭振时,作以下变量替换
(17)
将式(6)(16)(17)回代式(8),再结合式(4)(11)—(13)可得三轮多楔带附件驱动系统在张紧臂平衡位置处几何线性化后的控制方程,整理为矩阵形式,可得:
(18)
(19)

(20)
(21)
在式(18)-(21)中,[φ2(ω)φ3(ω)φt(ω)]T可视为系统的状态量,[φ1(ω)]为系统的输入量,[Mt(ω)]为系统中的非线性量。
2 多楔带附件驱动系统时域稳态响应求解
2.1 HB-AFT法的原理
时频域切换技术的核心思想是在时域中求非线性力,在频域中求解控制方程[16]。时频域切换技术与谐波平衡法结合,可以进一步提高计算效率。HB-AFT法的原理与计算步骤如下。
对于一个非线性系统,其控制方程一般可以整理为如下的形式[17]:
(22)
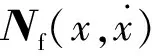
将式(22)转换到频域可得:
L{ω,X(ω)}=F(ω)+Νf(ω,X(ω))
(23)
根据谐波平衡原理,系统的状态量、非线性力以及外激励均可表示为谐波函数叠加的形式[20]:
(24)
式中:ω0为外激励的基频,k为谐波阶次,H为截断阶次。
当外激励F(t)已知时,只需要求出谐波系数ak和bk,则可以确定系统的响应情况。
步骤1:迭代初值的求解

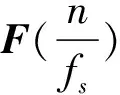
(25)
3)假设非线性力为0,即ek和fk均为0向量。将式(24)(25)代入式(23),可得方程:
(26)
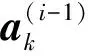

(27)
步骤2:迭代求解过程
(28)
(29)
2)对非线性力的时域序列式进行离散傅里叶变换,得到对应的谐波系数:
(30)
3)将式(24)(25)(29)代入式(23),可得方程:
(31)
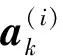
(32)
4)当需要的计算精度为1%时,如果相邻2次求得的谐波系数满足式(33),可认为迭代过程收敛,系统的响应为式(34)。
(33)
(34)
式中:||·||1和||·||∞分别代表向量的1范数和无穷范数,P为系统的自由度数。
2.2 时域稳态响应求解
对一个已知系统参数以及激励大小的三轮多楔带附件驱动系统,可以使用HB-AFT法计算其稳态响应。计算流程如图7所示。
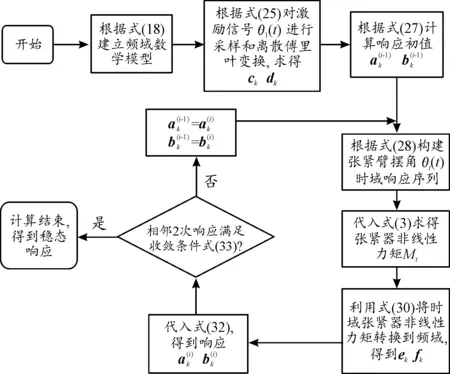
图7 使用HB-AFT法计算多楔带附件驱动系统稳态响应计算流程框图
一个三轮多楔带附件驱动系统的系统参数如表1所示。

表1 三轮多楔带附件驱动系统的系统参数
利用HB-AFT法计算以下2种工况的稳态响应:
1)工况1:驱动轮的平均转速为600 r/min,只考虑2阶扭振,2阶扭振的扭振幅值为3°,初始相位为0。采样频率fs取1 000 Hz,采样时间T取1 s,截断阶次H取5。
2)工况2:驱动轮的平均转速为900 r/min,只考虑2阶扭振,2阶扭振的扭振幅值为2°,初始相位为0。采样频率fs取1 000 Hz,采样时间T取1 s,截断阶次H取5。
将4阶龙格库塔算法与迭代方法进行结合,计算三轮多楔带附件驱动系统的稳态响应的过程见图8。
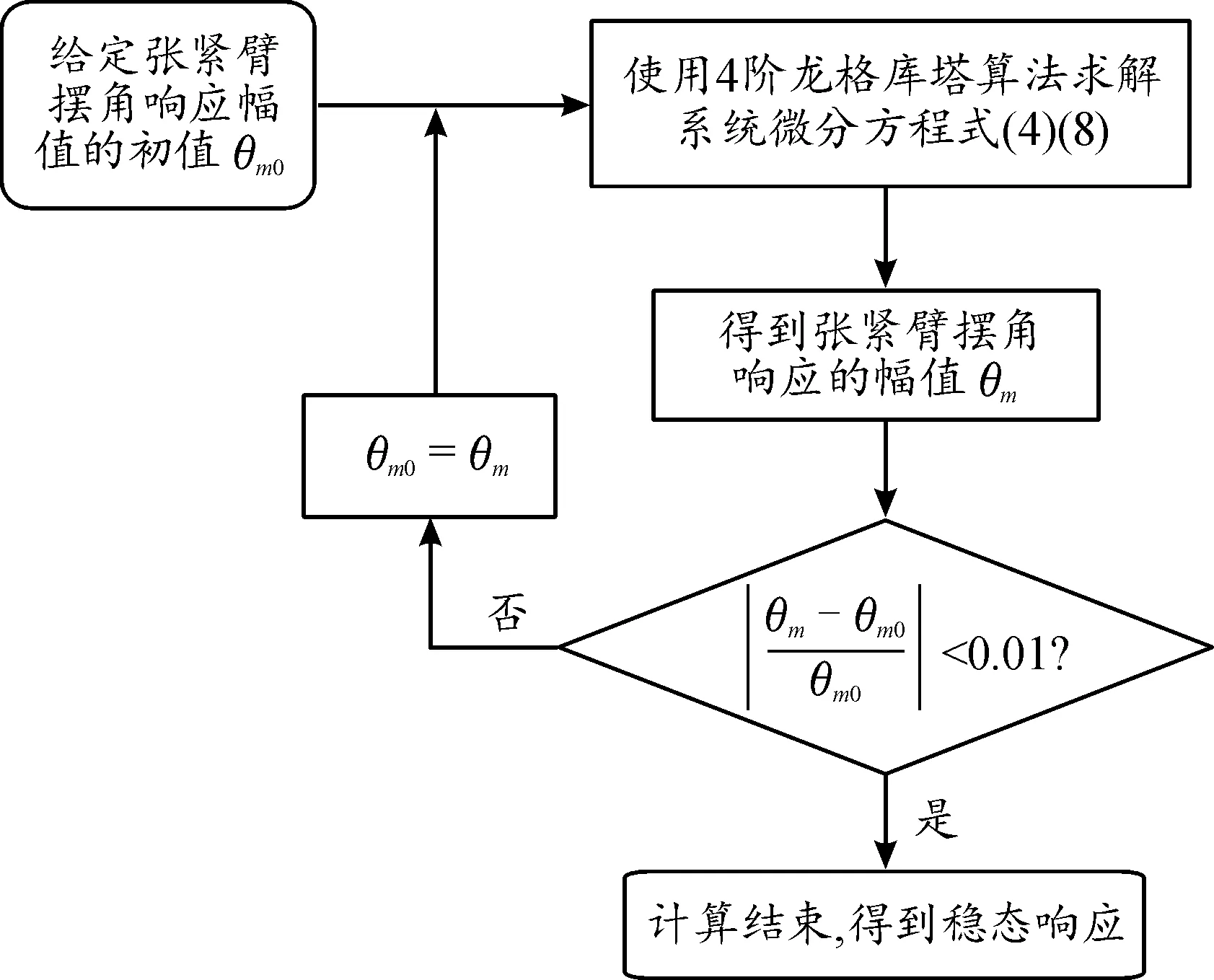
图8 使用数值迭代方法计算多楔带附件驱动系统稳态响应的过程框图
利用以上2种方法计算得到的张紧臂摆角的稳态响应如图9所示,稳态响应计算结果及计算时间见表2。
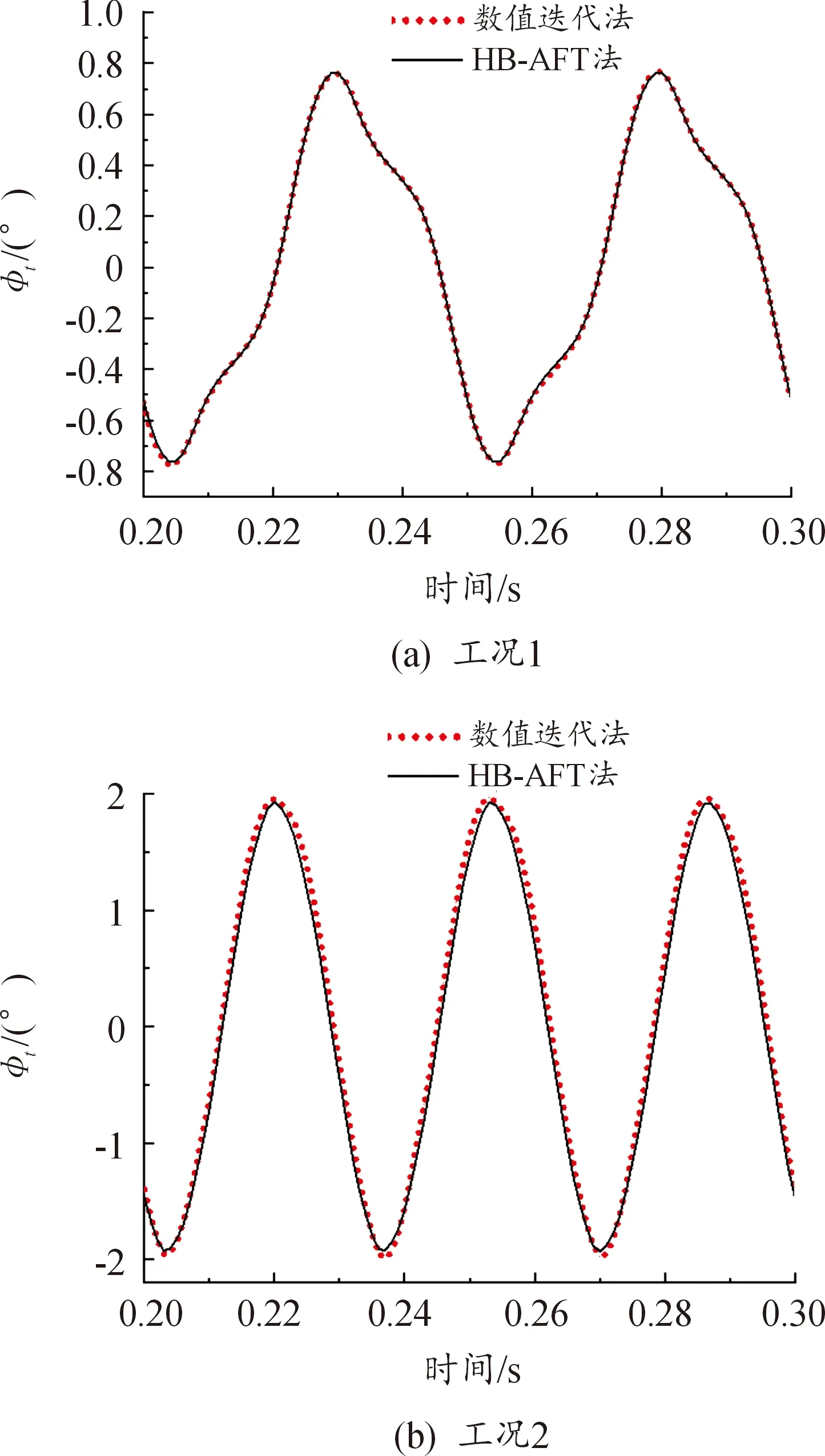
图9 张紧臂摆角的稳态响应曲线

表2 稳态响应计算结果及计算时间
由图9可以看到,2种计算方法求得的稳态响应的幅值和相位非常接近。从表2可知,当截断阶次H取5时,HB-AFT法已经有很高的计算精度,并且计算效率非常高,计算速度是数值迭代法的40倍以上。因此,HB-AFT是计算多楔带附件驱动系统稳态响应的一种高精度、高效的方法,基于此方法可以方便地开展参数分析以及优化的工作。
下面分析截断阶次H对计算精度的影响。选择工况1作为分析工况,截断阶次H依次取为1、3、5、7、9,根据图8的计算流程分别计算不同截断阶次下系统的稳态响应。计算结果以及误差分析见表3和图10。
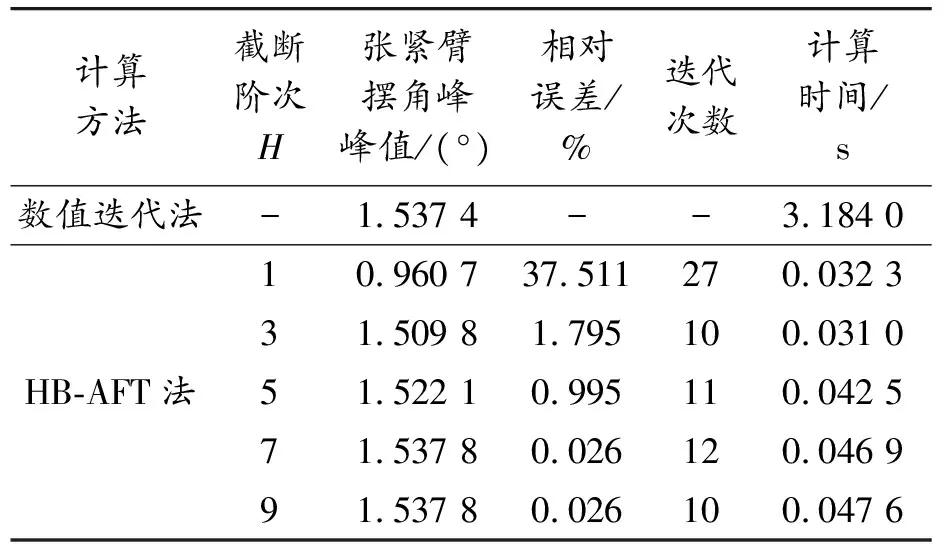
表3 不同截断阶次H下稳态响应计算结果
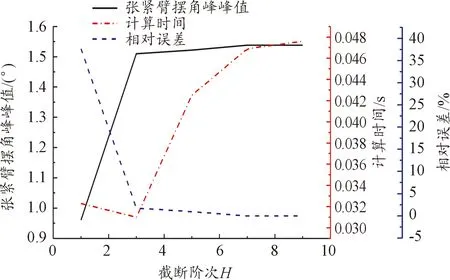
图10 计算结果、计算时间及相对误差随截断阶次H的变化曲线
由表3和图10可知,随着截断阶次H的增大,计算得到的张紧臂摆角峰峰值逐渐收敛于一个稳定值,相对误差逐渐减小。当截断阶次H取5时,已经有相当高的计算精度,相对误差小于1%。计算时间随着截断阶次H的增大呈现出先减小后增大的趋势。截断阶次H为1时计算时间不是最小的原因是,在计算过程中忽略了高阶谐波响应,导致计算误差偏大。计算误差偏大使迭代过程不容易收敛,因此需要进行更多次的迭代计算,使消耗的计算时间增多。由于非线性系统不具有频率保持性,在计算过程中不能忽略高阶谐波响应,只保留1阶谐波会引起较大的计算误差。因此,在使用HB-AFT法计算多楔带附件驱动系统的稳态响应时,截断阶次H建议取5或7,此时兼具较理想的计算精度与计算速度。
3 结论
以三轮多楔带附件驱动系统为研究对象,在一定的扭振激励下,采用HB-AFT法求解了系统的稳态响应。采用HB-AFT法计算多楔带附件驱动系统的稳态响应能够解决张紧器的输出力矩与响应幅值相互影响的问题,并且具有高精度、高效率的特点。保留5阶谐波进行计算时,与传统的数值迭代法相比,响应的相对误差小于1%,而计算速度提高40倍以上。张紧臂的摆角响应中除了含有激励频率的频率成分,还包含一些高次谐波成分。在计算时忽略高次谐波成分,会导致计算精度下降,计算速度也得不到明显的提升。

