大学生的线上学习成效影响因素分析——以微积分课程为例

杨松林，邵永存，徐 婷

(1.苏州城市学院，江苏 苏州 215104；2.苏州大学 东吴学院，江苏 苏州 215000)

新冠肺炎疫情的来临打破了高校原有的线下教学模式，在“停课不停教，停课不停学”的背景下，我们开展了微积分课程的线上教学。微积分课程是本校工科专业的一门重要基础课，内容抽象，学习难度较高，对学生后继课程的学习和逻辑思维能力的培养起着重要作用。微积分课程教学团队利用自主教学资源基于超星学习平台开展线上教学，每次课前给出学习要领和学习视频的任务点，每周针对性地对章节的知识点进行一次课堂练习，随时掌握学生的学习成效。为尽量缩短线上教学与线下教学的差距，我们充分利用网络平台(腾讯课程、QQ 屏幕共享等)对微积分课程中的重点、难点及学生学习中出现的问题进行详细讲解，帮助学生仔细梳理和总结知识点。

经过一个学期的线上教学，我们对线上教学的成效和存在的问题进行了总结，对线上教学与线下教学进行了比较分析，为今后线上教学提出建议。在总结分析的同时，我们思考几个问题：(1)线上教学的效果如何评价？师生如何看待线上教学？是否满意？文献[2-6]等构建在线教学质量评价体系的基本原则，构建了基于评教与评学相融合的质量评价体系和线上教学的教学效果分析，普遍认为高校线上教学情况良好，教学效果较佳，师生的满意度较高。(2)有哪些因素影响学生的线上学习效果和学习成绩，以及这些因素对线上学习效果和学习成绩的重要性与支持度？我们从苏州大学文正学院2019 级通信专业中随机抽取20 名学生作为研究样本，以其微积分课程的期初平均成绩、课堂练习平均成绩、观看视频平均完成比例和作业完成等级作为影响学习效果与学习成绩的条件属性，基于属性依赖度和支持度分析的粗糙集数据挖掘方法，通过对各属性依赖度和支持度了解不同属性对决策的不同作用，得到这些学习数据的定性分析。

波兰数学家PAWLAK 于1982 年提出的粗糙集理论能够处理粗略数据与模糊数据，通过集合的边界区域而不是隶属函数来表达模糊性，是分析不确定现象的一个有效及科学的工具，因此被广泛应用于数据挖掘的属性约简、数据处理等方面。这一理论已经成为数学与信息科学最为活跃的研究领域之一，并在金融学、材料科学和教育学等学科得到了广泛应用。本文所涉及粗糙集理论中的一些基本概念均请参阅文献[7，9]。

一、学习数据粗糙集模型的建立

本文从苏州大学文正学院2019 级通信专业中随机抽取20 名学生作为研究样本，利用粗糙集理论的约简原理，剔除了一些“可依赖”和“可忽略”的影响因素，我们选取这些学生在2019 年至2020 年学年第二学期微积分(二)课程的线上学习数据：期初成绩、课堂练习成绩、观看教学视频完成比例、作业完成等级和期末考试成绩作为分析数据(表1)。

说明：表1 中“期初平均成绩”为学生在2019 年至2020 年学年第一学期微积分(一)的课程平均成绩；“课堂练习平均成绩”为学生在本学期六次课堂练习成绩和四次章节练习成绩的加权平均值，课堂练习要求学生在15～20 分钟内完成3～4 道练习题，在规定时间内上传到教师端，这些练习完成情况能较为真实地反映学生的学习情况；“观看教学视频平均完成比例”为学生在本学期观看教学视频完成比例的平均值；“作业完成等级”为学生在本学期完成课后作业的综合情况；“期末考试平均成绩”为学生的本学期期末考试平均成绩，而非学期成绩。

为了用粗糙集方法分析线上学习数据，需要建立线上学习数据的信息系统S={U，C∪D}。信息系统S 中论域U 为表1 中20 名学生的集合，并用u，u，…，u分别表示表1 中的20 名学生；条件属性集C 为{c，c，c，c}，其中c，c，c，c分别表示期初平均成绩、课堂练习平均成绩、观看教学视频平均完成比例(%)和作业完成等级；决策属性集D 为{d}，其中d 表示期末考试平均成绩。

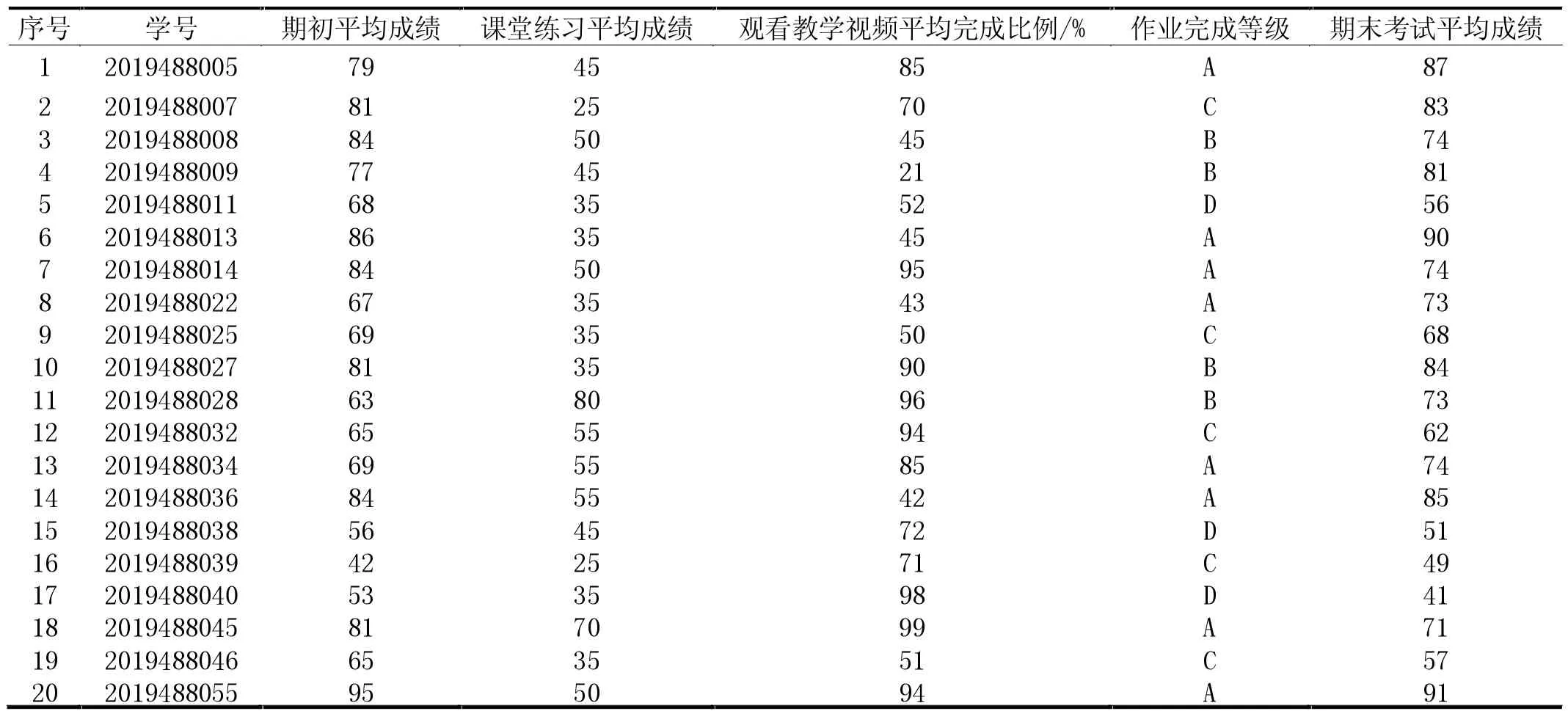
表1 微积分(二)线上学习数据表

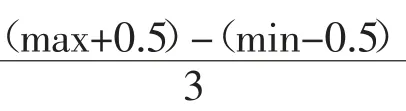
(1)对期初平均成绩c而言，全距为r=53，组距为h=18.0，采用等距分组法，其组区间为(41.5，59.5)，[59.5，77.5)，[77.5，95.5)。因此我们用c表示期初平均成绩介于77.5 分与95.5 分之间；c表示期初平均成绩介于59.5 分与77.5 分之间；c表示期初平均成绩介于59.5 分与41.5 分之间。

(2)对课堂练习平均成绩c而言，我们用c表示课堂练习平均成绩介于61.9 分与80.5 分之间；c表示课堂练习平均成绩介于43.2 分与61.9 分之间；c表示课堂练习平均成绩介于24.5 分与43.2 分之间。

(3)对观看教学视频平均完成比例(%)c而言，我们用c表示观看教学视频平均完成比例(%)介于73.1与99.5 之间；c表示观看教学视频平均完成比例(%)介于46.8 与73.1 之间；c表示观看教学视频平均完成比例(%)介于20.5 与46.8 之间。

(4)对作业完成等级c而言，我们用c表示作业完成等级为A；c表示作业完成等级为B；c表示作业完成等级为C；c表示作业完成等级为D。

(5)d 为决策属性：期末考试平均成绩，我们用d表示期末考试平均成绩介于74.5 分与91.5 分之间；d表示期末考试平均成绩介于57.5 分与74.5 分之间；d表示期末考试平均成绩介于40.5 分与57.5 分之间。

基于表1 和上述离散说明(1)到(5)，我们得到信息系统S 的决策表(表2)。

表2 微积分(二)线上学习数据决策表

二、学习数据对期末考试成绩的重要性和支持度

根据线上学习数据信息系统S 的决策表(表2)，我们通过计算信息系统S 的相关粗糙集和正域得到正域元素个数，见表3。

表3 信息系统S 的正域元素个数

(一)期末考试平均成绩对学习数据的依赖度

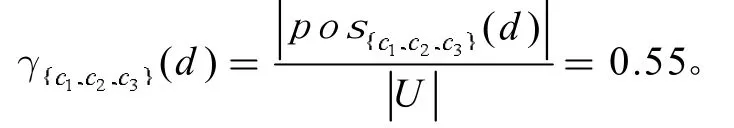
按照上述方法，依次去掉其他属性以求取剩余条件属性的依赖度，结果见表4。

表4 期末考试成绩对学习数据的依赖度

其中：依赖度是决策属性d 关于条件属性c，c，c与c，c，c和c，c，c以及c，c，c的依赖度。如图1 所示。

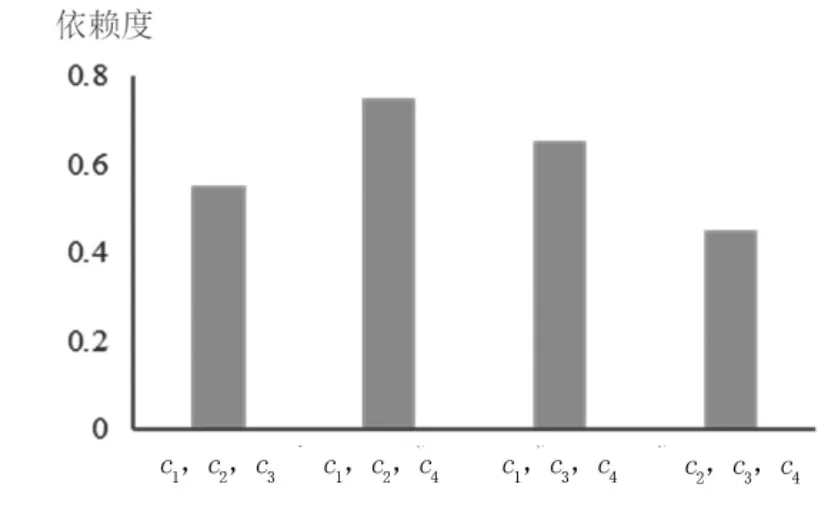
图1 期末考试成绩对学习数据的依赖度

当去掉的条件属性不同时，剩余条件属性组合的依赖度也不同，表明被去掉的条件属性对决策属性的影响也是不同的，各条件属性组合对决策属性的影响程度从大到小排序为组合c，c，c>组合c，c，c>组合c，c，c>组合c，c，c。

由此可见，条件属性c对决策属性d 的影响大，条件属性c对决策属性d 的影响小。

(二)学习数据对期末考试成绩的重要性

依据表4，我们通过公式(2)计算出各条件属性对决策属性的重要性，见表5。

表5 学习数据对期末成绩的重要性

条件属性子集C′关于决策属性d 的重要性为：

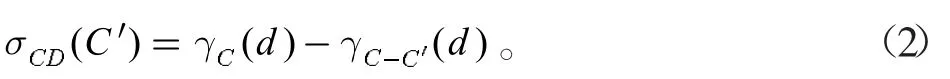
由公式(2)计算得

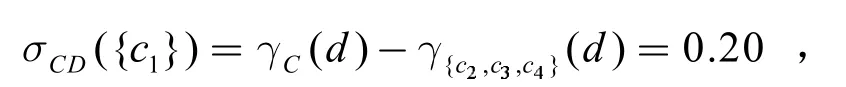
其中σ 值越大，说明条件属性对决策属性的重要性越高。

在表5 中，重要性是条件属性c(k=1，2，3，4)对于决策属性d 的重要性。表中c的重要性为0，并不表示c对决策属性d 无影响，这里的重要性是相对的，注重的是重要性的顺序。如图2 所示。

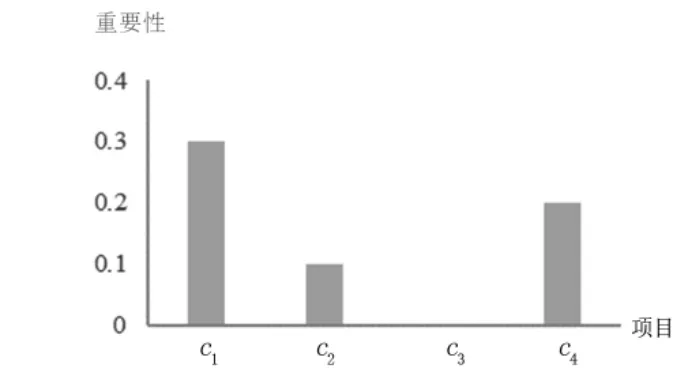
图2 学习数据对期末考试成绩的重要性

表5 表明各条件属性对决策属性的重要性从大到小排序为属性c>属性c>属性c>属性c。由此我们获得条件属性对决策属性的影响程序的排序。

(三)学习数据对期末考试平均成绩的支持度

通过公式(3)计算得决策属性d 关于条件属性c(k=1，2，3，4)的支持度为：

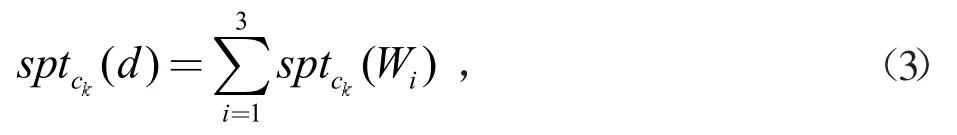
其中W，W，W为等价类U/D 的三个子集。由公式(3)计算得spt(d)=0.15，spt 值越大，说明该条件属性对决策属性的支持越大，则该属性对决策属性的影响越大。按照上述方法，计算各条件属性对决策属性的支持度见表6。

表6 学习数据对期末考试成绩的支持度

在表6 中，支持度是条件属性c(k=1，2，3，4)对决策属性d 的支持度。表中c的支持度为0，并不表示c对决策属性无支持，这里的支持度是相对的，注重的是支持度的顺序。如图3 所示。

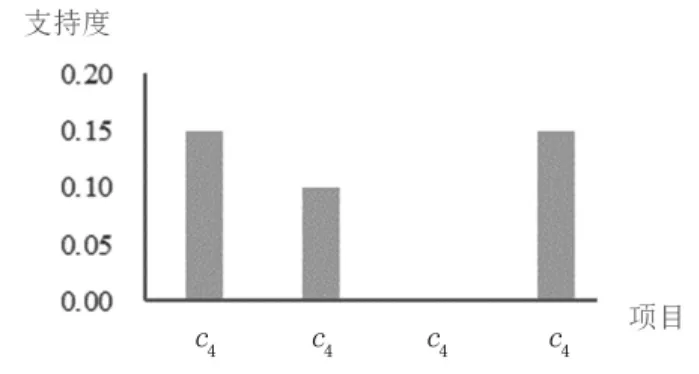
图3 学习数据对期末考试成绩的支持度

三、结论与讨论

根据第二部分的讨论，我们得到下列结论。

1.“期初平均成绩”的重要性最高，“期初平均成绩”是微积分(一)的成绩，也即微积分(一)成绩的重要性最高，这与“多元微积分的基础是一元微积分”相吻合，进一步强调了一元微积分的重要性，也说明了基础的重要性；多年线下教学中，我们也发现学生一元微积分的掌握程度直接影响到多元微积分的学习。

2.“作业完成等级”的重要性其次。验证了“学生作业的完成情况良好对学生的成绩有较大正向的影响关系”。学生能够独立且较好地完成作业，一方面说明学生的学习态度认真，学习主动性比较高；另一方面说明学生较好地掌握了相关知识。

3.“课堂练习平均成绩”的重要性比“作业完成等级”的重要性低，从表1 可以发现有些学生“课堂练习平均成绩”比较低，而“作业完成等级”和“期末考试平均成绩”比较好。一方面说明一些学生在线上课堂的学习中接受能力一般，课堂掌握程度一般，但学生课后及时消化了线上课堂学习的知识，并能够对线上学习的知识进行反思和概括；另一方面说明这些学生学习态度比较认真，线上课堂没有掌握的知识，课后主动学习和复习，认真完成课后作业。

在线下教学过程中，教师通过面对面授课进行实时互动，能较为直观地了解学生的学习状态，但也增加了学生对教师的依赖性。而在线上教学模式下，学生降低了对教师监督的依赖性。化被动为主动，学生的自主学习能力得到一定的锻炼。在线上教学中，我们发现问问题的学生数比线下教学时大幅提高，对线上课堂学习中没有理解的内容、有疑问的内容和作业中遇到的问题等，学生会建立学习共同体，相互探讨，相互讨论；或通过QQ 等工具向老师提问，这是线上教学的优点。

4.“观看教学视频平均完成程度”的重要性相对最低，这与我们的认知相差甚远。我们一直认为大一学生刚从高中阶段的“填鸭式学习”转变过来，他们的自主学习能力和自学能力相对较弱，因此在线下教学时，我们一直强调听课的重要性。这对我们今后的教学有一定的指导意义，说明我们的教学观念和方式亟须改变。文献[13]研究表明教师采用课堂讨论越多及师生互动程度越高，学生主动学习水平越高。因此，我们在今后的线上教学过程中要改进教学方式，采用直播方式，教学过程中多与学生互动，充分发挥学生的主观能动性，培养学生的自主学习能力和自学能力。

“观看教学视频平均完成比例”的重要性相对最低，也解释了“部分同学观看教学视频完成比例为0(我们在选择统计样本时剔除了特殊情况)，但期末成绩大于60 分”的情况。一方面，学生长时间面对着计算机学习，容易疲劳，容易孤独，容易失去学习兴趣；另一方面，由于“教师的不在场”使学生在学习和心理方面的支持不够，导致了学习效果不尽如人意。建议教师在进行线上教学前要告之学生在线上教学中可能出现的问题，正确地引导学生进行线上学习；要重建“师生共场，打通学生与世界的藩篱”，构建虚实结合的教学情境，消除空间上隔阂，给学生提供一个“教师与你同在”的学习情境，最终化解线上教学的不足。最后，在线下教学过程中，教师通过面对面授课进行实时互动，能较为直观地了解学生的学习状态，可以根据学生的学习状态及时调整课堂教学内容，但线上教学无法做到。因此对于线上教学客观环境的改变，教师需要重新思考线上教学课程的内容和结构，对学习资源进行整合和更新，以有利于学生的线上学习，并通过远程提问、课堂练习、线上讨论等及时了解学生的学习情况。

5.“期初平均成绩”和“作业完成等级”的支持度为0.15，相对较高，“观看教学视频平均完成比例”的支持度相对最低，这与它们的重要性指标完成吻合。

对学生线上学习效果有影响的因素，除了本文所讨论的四个因素，还有许多，如学习的主动性、学习方法、智力水平、学习环境等。我们计划就影响学习效果的因素对学生进行一次问卷调研，掌握更多的资料，进行更深层次的研究分析。

本文以微积分课程为例分析了线上学习影响因素对于学习成绩的重要性和支持度，得到一些定量指标，希望分析结果对于教师的线上教学和线下教学有一定的借鉴意义。