面向大规模网络测量的数据恢复算法：基于关联学习的张量填充

欧阳与点，谢 鲲，谢高岗，文吉刚，4

（1.湖南大学信息科学与工程学院，湖南长沙 410006；2.中国科学院计算机网络信息中心，北京 100089；3.中国科学院大学，北京 100089；4.湖南友道信息技术有限公司，湖南长沙 410006）

1 引言

网络吞吐量记录了端到端网络成功传输数据的速率，是衡量网络性能的重要指标.获取全网端到端吞吐量对于了解网络状态、跟踪服务等级协议和定位网络故障等应用［1～3］至关重要.然而，由于测量代价大，现有的网络监控系统难以获得完整准确的全网吞吐量测量值.本文中吞吐量定义为单位时间内端到端网络源节点成功向目的节点传输的实际数据量，不包括包头，并且重传的数据包只计算一次［4］.测量网络吞吐量通常需要从源端向目的端传输一个大的文件，并测量完成文件传输所需要的时间，再将文件大小除以传输时间来计算吞吐量［5］.这种方法会产生大量测试流量，影响网络性能.一些数据包流级别的直接测量技术［6，7］通过跟踪经过设备的数据包将具有相同源-目的地址的数据包汇聚成一个流作为该源-目的地址之间的流量即吞吐量，这种方法可以做到准确测量，不会被背景流量干扰.但是由于缺乏支持设备以及测量开销等原因，直接测量只能够测量部分源-目的地址之间的吞吐量［8］.尽管现在已经有成熟的网络监控系统可以实时测量网络时延，比如微软Pingmesh［9］通过发送探测数据包能够测量大规模数据中心网络中任意两个服务器之间任何时刻的时延，获取每对节点之间任意时刻的吞吐量测量值仍然很困难.

近年来，有研究表明端到端网络性能数据具有隐藏的时空相关性［10］，提出了稀疏网络测量技术.稀疏网络测量技术基于采样的方式降低测量代价，仅测量部分路径和时隙的数据，推测全部数据，将网络测量问题转换成从部分测量值估计全部测量值的数据恢复问题.目前主要有3 种典型的稀疏重构技术：压缩传感、矩阵填充和张量填充.作为一维向量和二维矩阵的高阶推广，张量模型可以充分利用多线性结构，挖掘高维数据之间隐藏的内在联系，达到更好的数据恢复精度.尽管前景光明，现有的张量填充算法针对网络性能数据恢复的研究现状仍然具有很大局限性，具体表现在其算法只考虑了单个网络性能指标的数据恢复，忽略了多个网络测量指标的关联信息.

实际的网络监控系统通常会涉及多个网络性能指标的测量，包括吞吐量、往返时延、丢包率等.有些指标的测量开销比较小，如测量往返时延只需要在源端记录探测数据包发送和到达的时刻，并计算时间戳之间的差值即可.现有的稀疏测量技术没有考虑多指标测量的应用场景，为了保证数据恢复的准确性仍然需要一定比例的吞吐量测量值，为网络带来较大的负担.由于网络中存在低测量开销的指标，同时考虑多个指标间的关系和测量代价，利用低开销的指标推测高开销的指标能够减少高开销指标的测量数量，进一步降低网络测量代价.此外，稀疏测量技术对单个指标在进行数据恢复时忽略了其他测量指标带来的附加信息，考虑到不同的指标之间具有相关性，在利用时空相关性进行稀疏重构的同时加入其他测量指标的外部辅助信息可以提高恢复精度.

基于上述思路，本文提出了一个面向大规模网络测量的数据恢复算法——基于关联学习的张量填充（Association Learning based Tensor Completion，ALTC）.在多指标联合测量背景下，构建从低测量开销指标到高测量开销指标的关联模型，在高开销指标吞吐量数据极少的情况下，尽可能测量低开销指标往返时延，借助关联模型从往返时延推测吞吐量，降低网络测量代价.在传统张量填充的框架中加入多指标关联信息，同时挖掘吞吐量内部的时空相关性和外部关联模型的辅助信息，进一步提高数据恢复精度.本文主要贡献总结如下：

（1）对真实网络数据集进行实验验证，分析了吞吐量与往返时延之间的关联，发现它们之间相关性强，但是关系复杂，难以用普通线性函数建模.针对该挑战，设计了一个基于神经网络的吞吐量-往返时延关联学习模型，捕获两个指标之间的关联，使用低开销的往返时延推测高开销的吞吐量，降低网络测量代价.

（2）由于吞吐量测量数据的内部也具有潜在的时空相关性，可以通过张量填充算法从部分测量推测全部数据.为了同时利用内部时空相关性和其他指标的外部辅助信息，使用关联学习模型的推测值对吞吐量的测量值进行预填充，并设计一个新的张量填充模型，同时拟合吞吐量的测量值和关联模型的推测值，设置关键参数误差平衡权重控制模型对测量值和对推测值的拟合程度，提高数据恢复精度.

（3）真实数据集上的实验结果展示了所提算法ALTC 在同样的吞吐量测量代价下可以显著提高数据恢复的精度.在采样率为2%的极低情况下，ALTC的恢复误差在传统线性张量填充算法的结果上改善了1.5倍，比目前主流的神经网络张量填充算法的误差降低了13%.

2 相关工作

从网络性能数据的部分测量值恢复未测量的缺失数据依赖于稀疏网络测量技术.最开始的压缩传感技术使用单纯的空间或时间信息重构缺失数据［11，12］.由于压缩传感主要作用于一维向量数据，应用范围受限，发展了矩阵填充技术使用简单的时空信息从低秩矩阵中恢复缺失数据［13，14］.然而，二维矩阵的形式在捕获数据潜在相关性上的作用仍然很有限，当数据缺失率较高时，恢复性能会受很大影响.为了克服基于矩阵方法的不足，一些新的研究基于张量填充技术，利用张量的多线性结构捕获网络测量数据更丰富的时空信息达到更精确的恢复效果［15～19］.张量填充算法依赖于张量分解，使用最广泛的张量分解模型有CANDECOMP/PARAFAC（CP）分解［20，21］和Tucker 分解［22］，其他模型都是对这两个模型的改进.

近年来有大量基于张量填充的网络数据恢复研究.Xie等人［15］寻找数据的更强局部相关性来形成和填充更低秩的子张量，恢复网络流量数据.Deng 等人［16］提出了一种基于杠杆分数采样的自适应张量填充方案估计个人设备网络的延迟数据.Wang 等人［17］考虑网络数据中的噪声和异常，将L2，1范数和LF范数引入张量填充模型中，估计网络流量.Xie 等人［18］基于Expectile 回归对张量填充不同数据点的拟合误差设置两种不同的权重，提高大象流的恢复精度.除了这些基于CP 分解或者Tucker分解的线性张量填充模型，Xie 等人［19］使用神经网络模型扩展传统张量填充算法的交互函数恢复网络监测数据，取得了很好的恢复精度.

然而，上述所有的模型或算法全都仅考虑单个网络性能指标，忽略了多个网络性能指标之间的关联，不仅数据恢复的精度受限，测量代价仍然很高.不同于现有研究，本文认为同时考虑多个网络性能指标的测量指标，多测量低开销指标、少测量高开销指标，挖掘指标之间的关联，利用低开销的指标辅助高开销的指标进行填充，同时使用数据内部的时空信息和指标外部的辅助信息，可以降低测量代价并提高数据恢复的精度.

3 问题建模和整体框架

3.1 问题建模

张量是高维数组，数组的维数又称为张量的模或者阶.如图1所示，本文将网络测量数据建模成I×J×K的三维张量，其中I，J和K分别表示网络中源节点的个数、目的节点的个数和测量的时间总数.令X 表示吞吐量张量，其元素xijk记录了源节点i与目的节点j之间在时间k的吞吐量测量值；令Y 表示往返时延张量，其元素yijk表示源节点i与目的节点j之间在时间k的往返时延测量值.如果源节点i与目的节点j之间在时间k没有吞吐量或往返时延测量数据，则X 或Y 中对应的元素为空.

图1 网络测量数据的三维张量模型

由于吞吐量的测量代价大，X 通常是带缺失值的稀疏测量张量.令Ω表示张量X 的测量样本索引集合，表示缺失样本索引集合.如果xijk已测量，则(i，j，k)∈Ω，反之(i，j，k)∈由于往返时延的测量方式简单，Y 为具有大量测量值的稠密测量张量.本文给出网络测量数据恢复问题如图2 所示，给定稀疏测量的吞吐量张量X在Ω上的少量测量值，与稠密测量的往返时延张量Y，建立吞吐量张量X 与往返时延张量Y 之间的关联，利用吞吐量的部分测量值和往返时延的关联估计X 的缺失值，恢复整个吞吐量张量.

图2 网络测量数据恢复问题

3.2 整体框架

为了充分利用多个网络性能指标之间的关联达到更高的吞吐量数据恢复精度和更低的测量代价，本文提出了一个面向大规模网络测量的数据恢复算法，即基于关联学习的张量填充（ALTC）.整体框架如图3 所示，首先研究了真实数据集中吞吐量与往返时延之间的关联，设计了一个使用往返时延推测吞吐量的神经网络关联学习模型（Y →X′），然后使用关联学习模型的输出对部分测量的吞吐量进行预填充（X，X′→），并在传统张量填充的架构上设计了一个组合的加权损失函数，同时利用预填充张量中往返时延的外部辅助信息和吞吐量测量数据的内部时空相关性更精确地重构完整的吞吐量张量

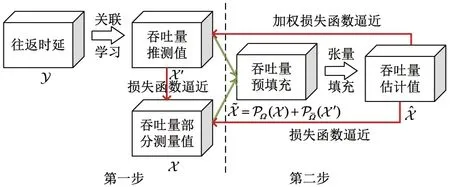
图3 基于关联学习的张量填充算法的整体框架

4 基于关联学习的张量填充算法

4.1 吞吐量与往返时延的关联

为了研究吞吐量与往返时间之间的关联模型，本文首先对真实网络数据集进行实验验证，分析吞吐量与往返时延之间的关联.WS-DREAM［23］数据集记录了142个用户在64个连续时间片（以15分钟为间隔）上的4 500 个Web 服务的服务质量测量结果，包括了吞吐量和往返时延.随机选取了数据集中的若干个源目的（即用户-服务）节点对，并绘制了其中4 组源目的节点对沿着64个时间片的测量值大小.如图4所示，横坐标为时间片的索引，纵坐标为测量值的大小，0 轴的上方为吞吐量大小，0 轴的下方为往返时延大小.图片显示当吞吐量持平时，往返时延也相对稳定；当吞吐量较大时，往返时延相对较小；当吞吐量较小时，往返时延相对较大.尤其当吞吐量极小时，往返时延很大，可能是由于发生了拥塞.

图4 吞吐量-往返时延关联

由此可知，同一网络结构下的吞吐量与往返时延之间存在强相关性，而且大体上成负相关.然而，由于在实际网络中不同的用户或服务具有不同的属性特征，难以使用简单的线性模型直接建模复杂的吞吐量和往返时延关系.这种复杂关系直观地表现在节点行为复杂，如两个具有相同大小的吞吐量源目的节点对的往返时延不一定相同.

4.2 吞吐量-往返时延关联学习模型

学习吞吐量与往返时延之间的复杂关系、从往返时延推测吞吐量的任务，直觉上类似于自然语言处理中的机器翻译，可以看作是序列到序列的问题，应用编码-解码（Encoder-Decoder）模型求解，即输入往返时延序列，输出对应的吞吐量序列.然而由于数据是部分缺失的，无论是提取吞吐量张量的切片矩阵还是纤维向量，都无法形成完整的吞吐量序列，使得编码-解码模型难以训练，推测精度不高.

根据3.2 节的分析，给定源节点i、目的节点j和时间k，在往返时延张量中与吞吐量xijk的值最相关的是对应位置上的yijk.然而，仅通过点对点的关系建模吞吐量与往返时延之间的复杂关联存在2 个局限性：（1）无法利用上下文信息，具体包括同一个源-目的节点对的测量值在不同时刻的变化以及同一时刻下不同源节点或目的节点类型对测量值的影响；（2）对异常和噪声敏感，当网络发生异常时会导致时延发生抖动，进一步导致对应吞吐量的预测值误差大.

在张量建模下，对于往返时延张量Y任意一个点yijk，分别保留下标i，j和k可变，而其他下标固定，可以提取3个纤维向量y：jk∈RI×1、yi：k∈RJ×1和yij：∈RK×1［24］.这3 个向量在张量Y中的交汇点为yijk，且分别对应了3 个坐标轴的上下文信息，其中y：jk表示不同源节点类型对当前目的节点和时间的影响，yi：k表示不同目的节点类型对当前源节点和时间的影响，yij：表示当前源-目的节点对在不同时刻下的变化.

基于以上分析，为了准确地建立吞吐量与往返时延之间的关联，通过往返时延推测吞吐量，本文设计了一个吞吐量-往返时延关联学习模型（Association Learning Model，ALM），提出了从纤维到元素（fibers to element）的推测框架.如图5 所示，给定源节点-目的节点-时间三元组(i，j，k)，关联学习模型首先提取纤维向量y：jk、yi：k和yij：作为输入，其中y：jk、yi：k和yij：分别代表源节点类型的影响、目的节点类型的影响、时序变化的影响，然后依次通过一个特征对齐模块和一个非线性映射模块来推测吞吐量xijk.

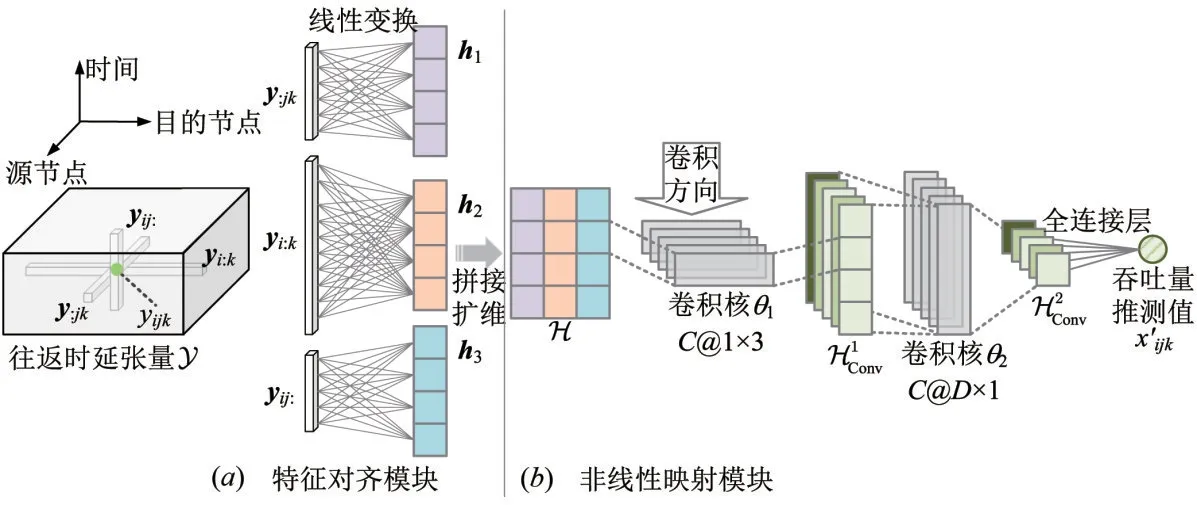
图5 吞吐量-往返时延关联学习模型(图中例子:特征维度D=4,卷积通道数C=5)

在特征对齐模块中，y：jk、yi：k和yij：首先各自进行一个线性变换提取特征，

其中，h1，h2，h3∈RD×1分别表 示y：jk、yi：k和yij：通过线性变换提取的特征向量，W1∈RI×D，W2∈RJ×D，W3∈RK×D为权重矩阵，b1，b2，b3∈RD×1为偏置项，D为特征维度.线性变换的主要目的是对齐3 个纤维向量的特征维度，为了最大程度保留纤维的原始特征，此处没有使用激活函数.再对特征向量h1，h2，h3进行拼接和维度扩展（expand_dims）操作，得到特征张量H.H 包含了往返时延yijk沿着张量3 个模的聚合信息，用于输入非线性映射模块来拟合吞吐量xijk.

非线性映射模块由2 个二维卷积层和1 个全连接层组成.第一层卷积核的大小为1×3，第二层卷积核的大小为D×1.令C表示通道数，即每一层卷积核的个数，θ1和θ2分别表示两层卷积的卷积核参数，ReLU(·)=max(·，0)表示激活函数，则卷积层的计算可形式化为

令x′ijk=f(y：jk，yi：k，yij：|Θ)表示式（1）～（4）的 吞吐量-往返时延关联学习模型，其中，Θ={W1，W2，W3，b1，b2，b3，θ1，θ2，w，b} 表示所有可训练参数的集合，选用均方误差（Mean Squared Error，MSE）作为损失函数，模型的优化目标可以形式化为

其中，|Ω|表示索引集合Ω的基数.梯度下降等算法可用于优化式（5），所有测量元素xijk，(i，j，k)∈Ω，可作为标签对模型进行点对点的有监督训练.在训练阶段完成后，对于吞吐量张量的任意缺失点(i，j，k)∈，可以提取往返时延张量Y 对应的纤维，输入训练好的模型，计算缺失点的吞吐量值，最终获取从往返时延推测出来的吞吐量张量X′.

4.3 基于关联学习的张量填充算法

在学习了往返时延和吞吐量之间的关联之后，如何有效地结合关联学习模型与张量填充算法，同时利用数据内部时空相关性和外部关联信息来提高吞吐量的恢复精度成为了关键.为此，本文提出了基于关联学习的张量填充模型.首先将由往返时延和关联学习模型推测出来的吞吐量张量X′与部分测量的吞吐量张量X合并为完整的预填充吞吐量张量

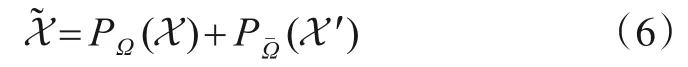
其中，PΩ表达到Ω的正交投影，如果(i，j，k)∈Ω，则[PΩ(X)]ijk=xijk；其他情况下，[PΩ(X)]ijk=0.PΩˉ同理.式（6）中，预填充的吞吐量张量保留了原始吞吐量张量的测量值，仅使用关联学习模型对缺失点的推测值，即当(i，j，k)∈Ω时，吞吐量在该位置具有测量值当时，吞吐量测量值在该位置缺失，使用往返时延和关联学习模型的推测值进行预填充

为了挖掘吞吐量测量数据内部的潜在特征，使用CP分解将预填充的吞吐量张量分解为3 个因子矩阵A∈RI×R，B∈RJ×R和C∈RK×R的形式，即其中R为张量的秩.令ai∈R1×R，bj∈R1×R和ck∈R1×R分别表示A的第i行，B的第j行和C的第k行，其物理意义分别为源节点i，目的节点j和时间k在潜在特征空间R1×R下的因子向量的每一个元素可用因子矩阵对应行向量的内积近似表示，即

在基于CP 分解的张量填充算法中，网络数据恢复问题被转换为张量填充问题，训练潜在因子向量ai，bj和ck，计算其交互，即内积，用于估计缺失的网络数据.传统张量填充算法通常以最小化测量点的测量值与CP分解的估计值之间的均方误差作为优化目标，如式（7）所示.对于每一个源节点-目的节点-时间三元组，式（7）基于源节点潜在特征因子、目的节点潜在因子和时间潜在因子之间的交互来建模吞吐量的值.

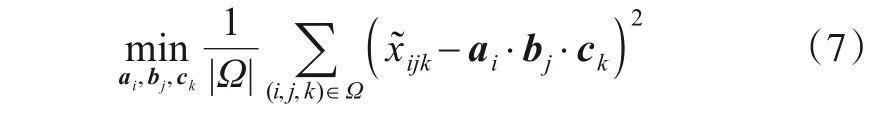
然而，传统CP 分解模型仅使用测量点的数据进行训练，无法有效地利用往返时延及其与吞吐量之间的关联.本文提出了一个组合的加权损失函数，在原有的目标函数中加入了往返时延的辅助信息.所提损失函数如式（8）所示，其中ρ表示关于(i，j，k)的二值函数：如果(i，j，k)∈Ω，则ρ(i，j，k)=1；反之如 果(i，j，k)∈，则ρ(i，j，k)=λ，λ∈(0，1)为事先指定的误差平衡权重.

式（8）整体上利用CP 分解因子向量ai，bj和ck的交互值对预填充张量进行逼近，不仅追求对测量值的最小重构误差，还追求对往返时延和关联学习模型所推测数据的最小重构误差，达到了同时利用时空相关性和关联信息的效果.细节上使用二值函数对两部分的重构误差分配了不同的权重进行区分，使得模型的训练更灵活.类似于同时执行的多任务学习模型，主任务是学习吞吐量测量值的特征，辅助任务是学习往返时延关联信息的特征.辅助任务与主任务的目标是一致的，因为借助往返时延和关联学习模型预先推测的吞吐量也是由吞吐量测量数据训练获得的.加权的辅助任务是必要的，它可以充分利用辅助信息往返时延及其与吞吐量之间的关联，并且能够扩充训练数据集，提高模型泛化能力，改善主任务的重构精度.

图6 为所提框架求解张量填充问题的主要步骤，包括：（1）组合测量张量与推测张量获得预填充张量；（2）基于CP 分解，使用测量样本和推测样本同时训练潜在因子向量；（3）使用训练好的潜在因子向量估计张量元素.在获得了3 个因子矩阵A，B和C之后，吞吐量张量可以用恢复，其元素为

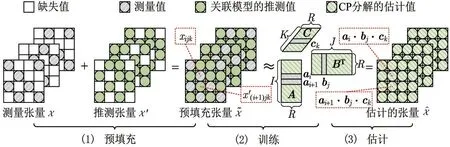
图6 基于关联学习的张量填充算法的步骤

4.4 详细算法流程

算法1 总结了基于关联学习的张量填充算法的完整流程，其中超参数的设置将在实验部分详细说明.在读取数据之后，首先训练吞吐量-往返时延关联学习模型，获得通过关联推测的吞吐量张量.再预填充吞吐量张量，训练基于关联学习的张量填充模型，最后计算吞吐量的估计值.

5 实验评估

5.1 实验设置

数据集为了评估所提算法的性能，本文在WSDREAM 数据集上执行了大量对比实验，将其建模成大小为142×4 500×64 的吞吐量张量和往返时延张量.原始数据集中，吞吐量的数据点占比为62.72%，往返时延的数据点占比为73.79%.仿真实验中，吞吐量张量的所有数据点按照p∶p∶1-2p的比例被划分为训练集、验证集和测试集，其中p∈｛2%，4%，6%，8%，10%｝为训练集所占比例，又称为采样率.吞吐量的采样率与吞吐量的测量代价成正比，采样率越高，测量代价越大.训练集对应于测量样本，测试集模拟缺失样本，验证集用于参数调优和计算迭代停止条件.往返时延的所有数据都用于训练关联学习模型，并在训练之前使用CP 分解对少量的缺失值进行预填充，使得应用场景更灵活.

评价指标本文使用2 个评价指标来评估数据恢复的准确性，分别是归一化的平均绝对误差（Normalized Mean Absolute Error，NMAE）和归一化的均方根误差（Normalized Root Mean Square Error，NRMSE），计算方式分别如式（9）和式（10）所示.

所有的实验结果都报告在测试集上，式（9）和式（10）中缺失样本索引集合特指测试集的样本索引，xijk为实际测量值为估计值.NMAE与NRMSE越小表示模型恢复性能越好.

实验条件所提模型部署在Pytorch 上，使用NVIDIA GPU，GeForce RTX 2060 上运行的CUDA 10.1对训练过程进行加速、Adam 小批量梯度下降算法对模型进行优化，ALM 的批大小设置为128，ALTC 的批大小为1 024，学习率都为10-4.实验中设置了2 个迭代停止条件，满足其一即可：（1）达到最大迭代次数1 000；（2）验证集上的损失函数连续50轮没有下降.

对比算法对比算法覆盖了传统的线性张量填充算法，包括CPals［25］、CPnmu［26］、CPwopt［27］、TKals［25］，前3个算法基于CP 分解，最后一个算法基于Tucker 分解；以及目前主流的神经网络张量填充算法，包括NTC［19］、NTF［28］、NTM［29］、CoSTCo［30］.

5.2 与传统线性算法对比恢复性能

图7 绘制了ALTC 与4 种传统线性张量填充算法在不同采样率下缺失数据的恢复误差曲线.随着采样率的增加，测量样本的增加，所有算法的恢复性能都随着NMAE 和NRMSE 的减少而增加.在所有的采样率下，ALTC 以更小的NMAE 和NRMSE 达到了更好的恢复性能.即使在数据非常稀疏（采样率2%）的情况下，ALTC的NMAE 和NRMSE 约为0.43 和0.45，而传统线性算法（CPwopt）的NMAE 和NRMSE 约为0.64 和0.76，分别是ALTC的1.5倍和1.7倍.这些结果表明，ALTC能够有效地挖掘并利用多指标的辅助信息，达到更好的恢复性能.

图7 ALTC在不同采样率下与传统线性算法对比恢复性能

5.3 与神经网络算法对比恢复性能

表1、表2记录了ALTC与4种神经网络张量填充算法在不同采样率下的缺失数据的恢复性能，其中表1为NMAE，表2 为NRMSE.如表所示，所有算法的恢复性能都随着采样率的增加变得更好，表现为越来越小的NMAE 和NRMSE.对比其他算法，ALTC 在当前采样率和评价指标下都达到了更低的恢复误差，说明在相同的吞吐量测量代价下，ALTC 的恢复效果更好.在采样率2%的情况下，ALTC 比目前主流的神经网络填充结果改进了(0.493 1-0.429 0)/0.493 1 ≈13%的NMAE 以及(0.528 6-0.447 8)/0.528 6 ≈15%的NRMSE.这进一步证实了所提算法的有效性，即使ALTC 是基于CP 分解架构的线性填充算法，训练参数也远小于复杂的神经网络模型，但由于很好地利用了多指标辅助信息，表现出了优异的性能.

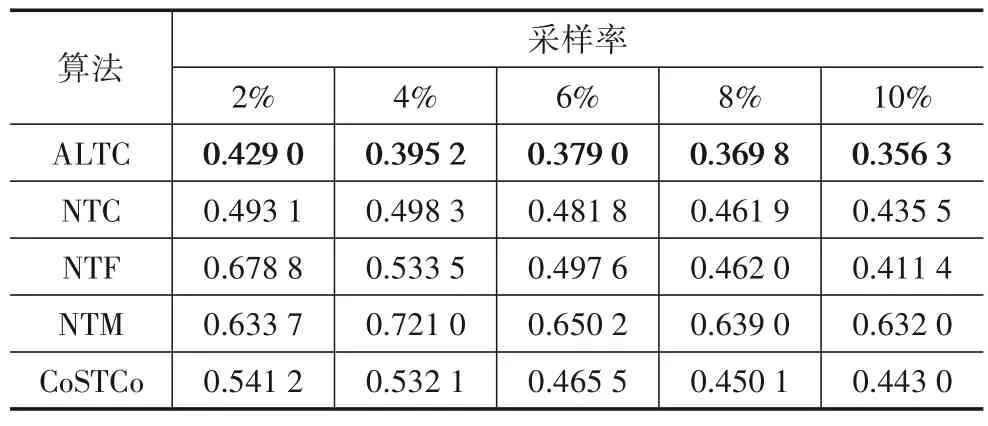
表1 不同采样率下与神经网络算法比较NMAE

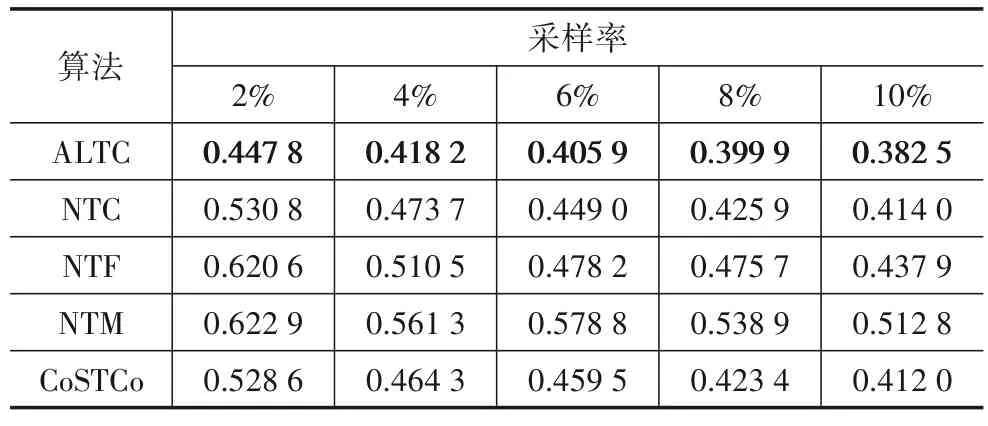
表2 不同采样率下与神经网络算法比较NRMSE

5.4 吞吐量-往返时延关联学习模型分析

图8 给出了仅使用关联学习模型ALM 通过往返时延推测吞吐量在不同吞吐量采样率下的推测效果.为了更直观地展示，同样绘制了ALTC 的恢复性能用于对比.通过图8 可以观察到，ALTC 比ALM 对于吞吐量指标的估计效果更好，因为ALTC 是在ALM 架构上的改进，验证了所提的基于关联学习的张量填充的有效性.对比表1、表2与图8中的结果，可以发现ALM与目前主流的神经网络张量填充算法相比仍然取得了非常有竞争力的性能，这表明了本文所提的关联学习模型在挖掘吞吐量-往返时延关联上的优越性.

图8 关联学习模型在不同采样率下的推测效果

如4.2 节所示，为了考虑上下文信息，关联学习模型输入为张量3个维度的纤维，对应于时间维度的变化以及不同源节点（用户）、目的节点（服务）类型的影响.为了研究最终的吞吐量值与不同上下文信息的关联性强度，固定采样率为10%，在图9 给出了考虑不同上下文信息的关联学习模型的推测效果.图9中，ALM 为原始模型，同时考虑了3 个维度的上下文信息，其他3 个模型是ALM 的变种：ALM-w/o-time 表示在输入时去掉时间纤维，仅考虑不同节点类型的影响；ALM-w/o-user表示在输入时去掉用户纤维，仅考虑不同服务节点类型和时间变化的影响；ALM-w/o-service 表示在输入时去掉服务纤维，仅考虑不同用户节点类型和时间变化的影响.可以观察到，在四个模型中，ALM的误差最小，说明三个维度的上下文信息对推测吞吐量的值都非常有效；ALM-w/o-user 的误差最大，说明考虑不同的用户节点类型对恢复效果的收益最大，即不同的用户节点类型与最终的吞吐量预测值最相关.

图9 考虑不同上下文信息的关联学习模型的推测效果

5.5 超参数研究

本节描述了关键超参数（ALM 的特征数D、通道数C和ALTC 的秩R、误差平衡权重λ）对模型性能的影响，其中采样率固定为10%.为了避免繁琐的超参数搜索，设定以下条件：（1）对ALM 和ALTC 的超参数进行单独调优，即ALM 的参数仅根据其对吞吐量的推测效果决定，不依赖于后续的ALTC 的填充效果；在找到了ALM的最优参数之后，再固定ALM 搜索ALTC 的最优参数；（2）固定ALM 的特征数等于通道数；（3）每次仅变化一个超参数而固定其他，找到可以达到最佳恢复性能的值.

特征数D、通道数C 的影响特征数D和通道数C都表示了模型将往返时延纤维转换成吞吐量值时设定的特征数.D和C越大，可表示的特征数越多，模型的参数规模越大.图10（a）绘制不同特征数和通道数对ALM 推测性能的影响.随着D和C的增大，模型的推测性能随着NMAE 和NRMSE 的减少而提高.一开始误差快速下降，当D和C超过30 后，误差下降速度变缓.考虑到模型复杂度与精度的平衡，本文根据结果设定ALM的特征值和通道数D=C=30.

张量秩R 的影响张量秩R也表示了模型可以捕获的潜在因子的特征维度，它直接影响了模型的参数规模.R越大，提取的特征维度越多，模型需要训练的参数也越多.图10（b）绘制了不同的秩对ALTC 恢复性能的影响.一开始随着R值的增加，模型的恢复性能随着NMAE 和NRMSE 的减少而提高.当R超过20 后，随着R值的增加，模型的恢复性能反而会降低.这是由网络测量数据的低秩特征决定的，R表示使用CP 分解表示吞吐量张量的秩，恰当的低秩可以更好地拟合完整的张量数据，而过大的秩会导致参数量增大，模型对训练集的拟合能力变强、泛化能力变差，即过拟合.因此，在ALTC的设定中，R=20.

误差平衡权重λ 的影响如式（8）所示，损失函数中的λ是为了在模型训练过程中平衡对测量值的拟合程度和对推测值的拟合程度.λ越小，模型拟合测量值的程度越大；λ越大，模型拟合推测值的程度越大.图10（c）绘制了不同的误差平衡权重对模型恢复性能的影响.一开始随着λ的增大，模型的恢复性能得到了提高.当λ超过0.01 之后，恢复性能随着λ的增大开始下降.这说明了为模型选择合适的λ可以帮助提高模型的恢复精度和泛化能力.因此，在ALTC 的设定中，λ=0.01.

图10 不同的超参数对模型性能的影响

5.6 复杂度分析

如算法1所示，本文提出的模型可以分为独立的两个训练步骤：ALM 和ALTC.由于ALTC 是基于CP 分解架构的线性填充算法，相比于传统的线性张量填充算法，仅需要额外的开销用于训练ALM，其训练参数集合Θ的总数据量为(I+J+K+C+3)D+4C+1.表3给出了采样率10%下不同模型的训练时间.ALM 训练一批数据的时间最长，即单位训练时间最长，因为需要更多的时间学习从往返时延到吞吐量复杂的映射关系，而且在实际应用中，可以用历史数据事先将ALM 训练好，在数据恢复时直接使用，大大加快填充速度.ALTC 训练一轮全部数据需要的时间比CP 分解需要的时间更长，即全部训练时间最长，因为训练数据更多，当采样率为10%时，CP分解只有10%的吞吐量测量值用于训练，而ALTC 有10%的吞吐量测量值和90%的吞吐量推测值用于训练，是CP分解的10倍.

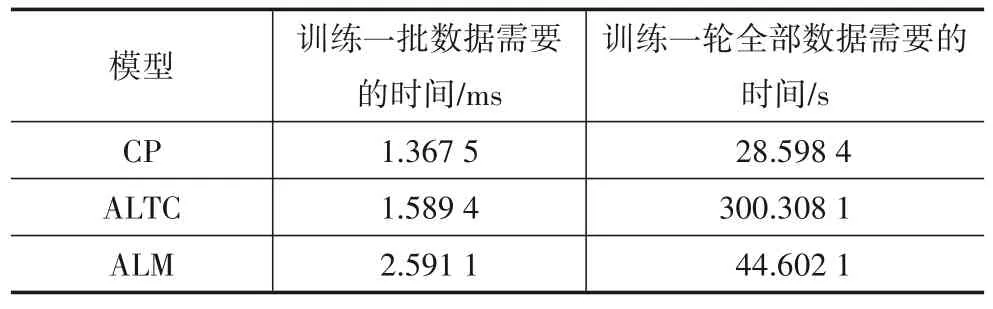
表3 训练时间对比

6 结论

本文提出了一种新的面向大规模网络测量的数据恢复算法，即基于关联学习的张量填充（ALTC），针对网络监控系统难以获得全网吞吐量测量数据的问题，利用吞吐量内部的时空相关性和外部指标的关联，以低测量代价获取全部吞吐量数据.首先研究网络性能指标的实际关联，设计了吞吐量-往返时延关联学习模型，使用低开销的往返时延推测高开销的吞吐量，降低测量代价.为了利用多指标关联模型辅助吞吐量填充，提高数据恢复的精度，进一步将吞吐量的测量值与通过往返时延和关联学习模型的推测值合并为新的张量填充拟合目标，并设计新的张量填充模型，同时学习吞吐量测量值和来自于往返时延的推测值的信息，设置误差平衡参数平衡两部分误差的权重.真实数据集的实验结果表明在相同的吞吐量测量代价下，本文所提的数据恢复算法ALTC 的恢复误差在传统线性张量填充算法的结果上改善了1.5 倍，而且比目前主流的神经网络张量填充算法的恢复结果降低了13%的误差.