被动声纳粒子滤波检测前跟踪的检测门限设置方法

奚 畅，蔡志明，袁 骏

（海军工程大学电子工程学院，湖北武汉 430000）

1 引言

被动声纳因其隐蔽性高、抗干扰能力强、便于提取目标属性信息等诸多优点，被广泛应用于水下目标探测领域.检测前跟踪（Track-Before-Detect，TBD）方法是低信噪比条件下对目标进行检测和跟踪的有效手段，它采用未阈值化的传感器原始观测数据，通过时间上的观测累积提升信噪比，同时实现目标的检测和航迹提取［1］.典型的TBD 实现算法包括Hough 变换［2］、动态规划［3，4］、递推贝叶斯估计［5～7］等.其中，基于递推贝叶斯估计的TBD 方法通过引入目标运动模型和传感器观测模型，完整地体现了跟踪的思想，是当前弱目标TBD的研究热点.由于贝叶斯滤波中的后验概率密度往往不解析，工程上难以计算，因此通常选择基于蒙特卡洛采样近似的粒子滤波算法来实现，其精度可以逼近最优估计.

门限设置是目标检测问题中的关键，TBD 算法中目标的检测和轨迹提取是同时完成的，所以门限检测的对象是目标轨迹，当前TBD 检测门限的研究多针对动态规划算法［8～11］.对于粒子滤波TBD 算法，由于系统观测与目标联合状态之间的强非线性，以及计算过程中所涉及到的高维积分运算，很难定量地对门限设置准则、恒虚警性能进行分析.

目标出现的后验概率和没有出现的后验概率之比被称为似然比［12，13］.文献［14］基于序贯似然比检测方法中的门限设置准则［15］，利用给定的虚警概率和漏检概率计算目标存在概率的检测门限.文献［16］将序贯似然比检验和固定样本长度似然比检验相结合，希望以最小时延检测到目标存在和消失，但对于样本长度的设置缺乏理论分析.

非线性情况下很难通过解析表达式计算检测门限，一种解决方法是借助蒙特卡洛仿真［17］.文献［18］分别以目标存在概率和似然比作为检验统计量，用蒙特卡洛方法计算不同参数条件下的平均检测概率和平均虚警概率，进而选取最佳门限.针对蒙特卡洛方法计算量大的缺陷，文献［19］提出非相干积累检测方法，检验统计量服从广义极值分布，可获得检测概率、虚警概率以及门限的解析表达式.

采用固定的检测门限［20，21］难以稳定地控制系统的虚警率.文献［22］提出利用有目标和没有目标情景下的后验概率分布，根据其变化特点在不同的时刻采用不同检测门限.文献［23］从似然比检测形式入手，推导了检验统计量的表达式，得到了系统虚警概率同检测门限之间的关系，给出了检测门限的近似闭式解.但是，文献［23］假设有目标和没有目标情况下观测单元的输出分别服从莱斯分布和瑞利分布，而实际应用中常见的雷达、声纳传感器观测单元输出均服从指数分布［24］，尚无公开发表的文献对此情况下的检测门限设置问题进行讨论.

在目标检测跟踪领域，常需要根据Neyman-Pearson准则对目标进行检测，即需要按照系统要求的虚警概率设置检测门限.为实现此目标，本文针对粒子滤波检测前跟踪算法，在被动声纳观测量满足指数分布的情况下，设置对数后验概率比为检验统计量并对其进行简化，详细推导了检验统计量与系统虚警概率之间的关系，给出了检测门限的闭式解，利用蒙特卡洛仿真和海上试验数据验证了所提方法的可行性和有效性.

2 系统模型

2.1 目标状态模型

假设目标具备线谱特征，目标与观测站在同一水平面内做匀速直线运动，由于被动声纳探测场景下观测站和目标航速较低、相距较远，可近似认为目标位变率恒定，由于目标方位变化幅度较小且水下目标线谱频率较低，可近似认为相对运动导致的线谱多普勒频移恒定.在极坐标系下建立k时刻的状态向量为

其中，βk为目标方位为目标位变率，fk为目标线谱固有频率与多普勒频移之和，snrk为目标线谱信噪比.

状态转移方程为

其中，F与Q分别为目标匀速直线运动模型的状态转移矩阵以及过程噪声协方差矩阵.设T为观测时间间隔，q1，q2，q3分别为目标运动状态、目标线谱频率、目标线谱信噪比的过程噪声级，则有

状态Ek建模为二元一阶Markov 过程，其状态转移概率矩阵为

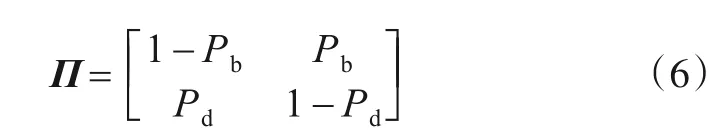
2.2 量测模型

被动声纳低频分析与记录（Low frequency analysis recording，Lofar）谱的横纵坐标分别为方位和频率，设观测的方位范围为分为Nb个方位单元，频率范围为分为Nf个频率单元，观测zk包括Nb×Nf个功率谱数据：

功率P(xk)与状态向量中信噪比snrk的关系为

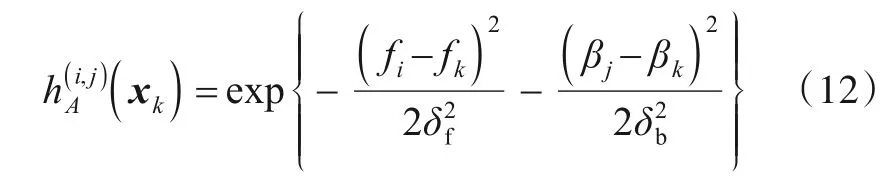
将式（9）和式（10）带入式（8），分析可知任意方位-频率单元的能量观测满足

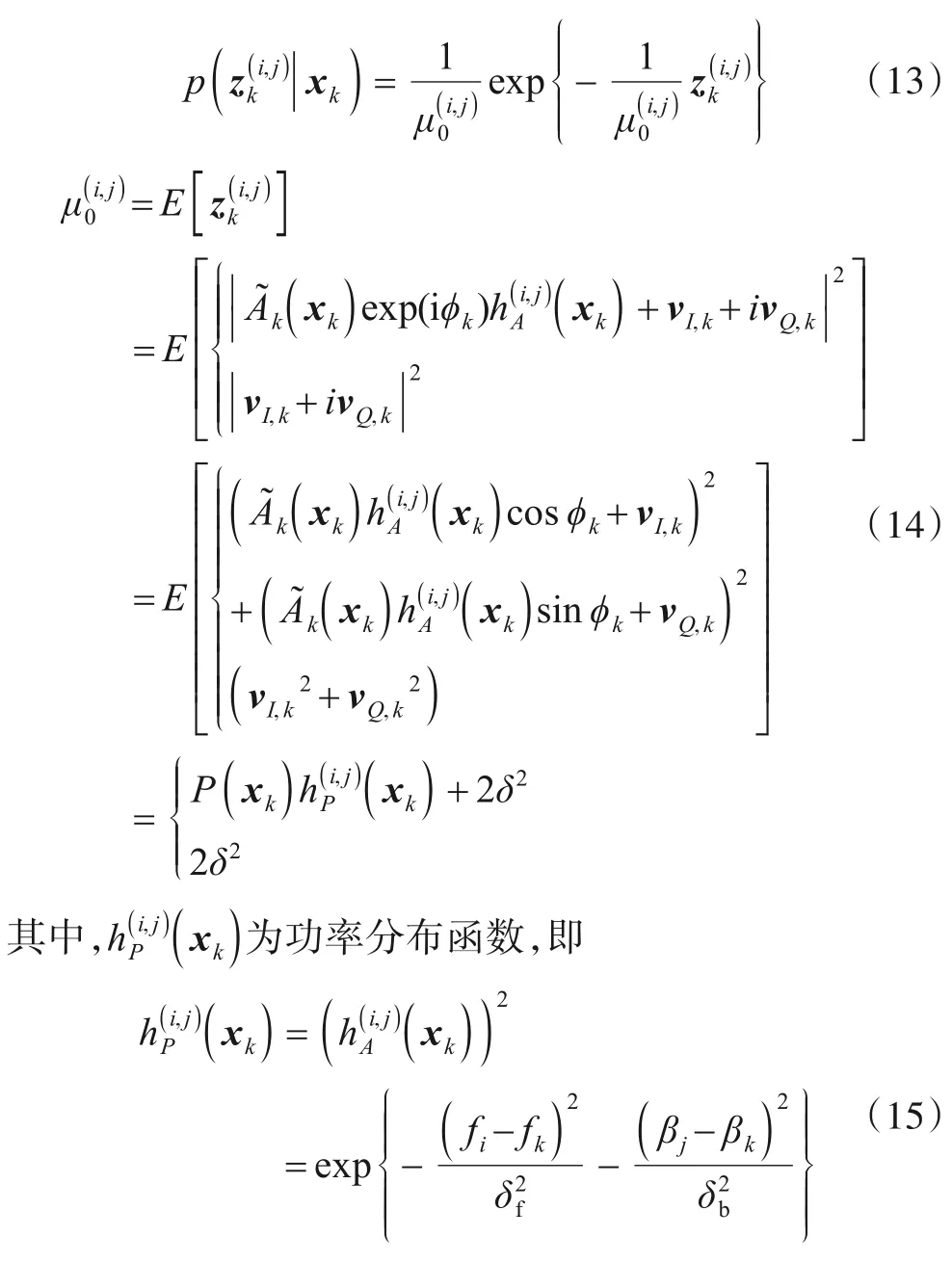
2.3 目标似然比

前述模型假设下，目标xk是否存在于分辨单元(i，j)内的似然函数可分别表示为

对于式（18）中的似然比，如果参与计算的观测区域过大，会带来超大的计算负荷.考虑到目标出现在某一位置时，通常只会对邻近区域的像素强度产生影响，因此在计算似然函数以及似然比时，可以选择部分分辨单元参与计算，以降低计算量.xk中元素βk和fk最接近的观测单元的索引标识为(ik，jk)，pi和pj为方位维和频率维的邻域参数，Cx(xk)和Cy(xk)分别表示受目标影响区域的索引标识集合，定义如下

3 粒子滤波检测前跟踪原理

从递推贝叶斯估计的角度，检测前跟踪问题可被阐述为：利用k-1 时刻目标状态xk-1及存在状态Ek-1的联合后验概率密度p(xk-1，Ek-1|zk-1)，结合最新观测信息zk，通过预测和更新两个过程递推地估计k时刻的联合后验概率密度p(xk，Ek|zk).

Ek=时观测区域内没有目标，讨论其后验概率密度没有意义，Ek=ek时联合后验概率密度函数p(xk，ek|Zk)的预测方程为

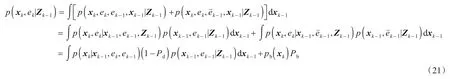
其中，p(xk|xk-1，ek，ek-1)为目标状态转移概率密度函数，pb(xk)为新生粒子状态概率密度函数.

当获知k时刻的量测值zk时，联合后验概率密度函数p(xk，ek|Zk)将更新为

其中，ℓ(zk|xk，ek)为似然比，p(xk，ek|Zk-1)为状态预测密度函数.

k时刻目标的存在后验概率可由式（22）积分得到

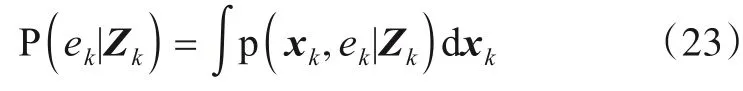
至此，已经得到目标状态的后验概率密度p(xk，ek|Zk)和目标的存在后验概率密度P(ek|Zk)推导式，理论上可以利用它们对目标进行检测和跟踪.但由于系统强非线性及运算中涉及到的高维积分，很难获得其解析形式，通常用基于蒙特卡洛方法数值计算的粒子滤波算法来实现.即通过搜寻一组在状态空间中运动传播的随机带权样本点（粒子）集对后验概率密度函数进行近似拟合，以样本点的加权平均值来替代概率密度函数的积分运算，从而获得系统状态的次优估计.

4 后验概率比计算方法

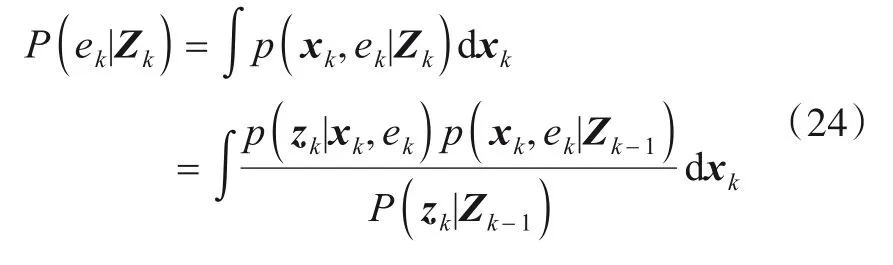
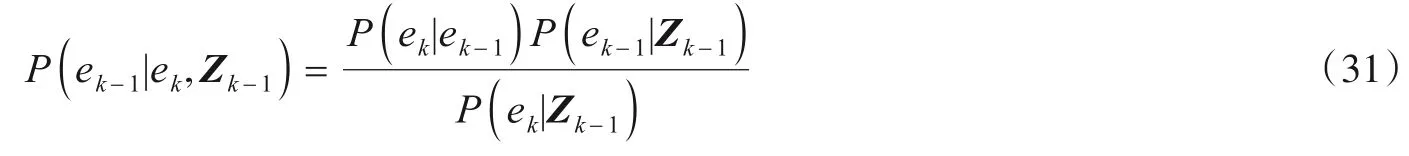
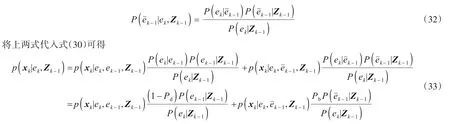
一般情况下目标新生概率Pb较小，若忽略新生密度函数的影响，可得

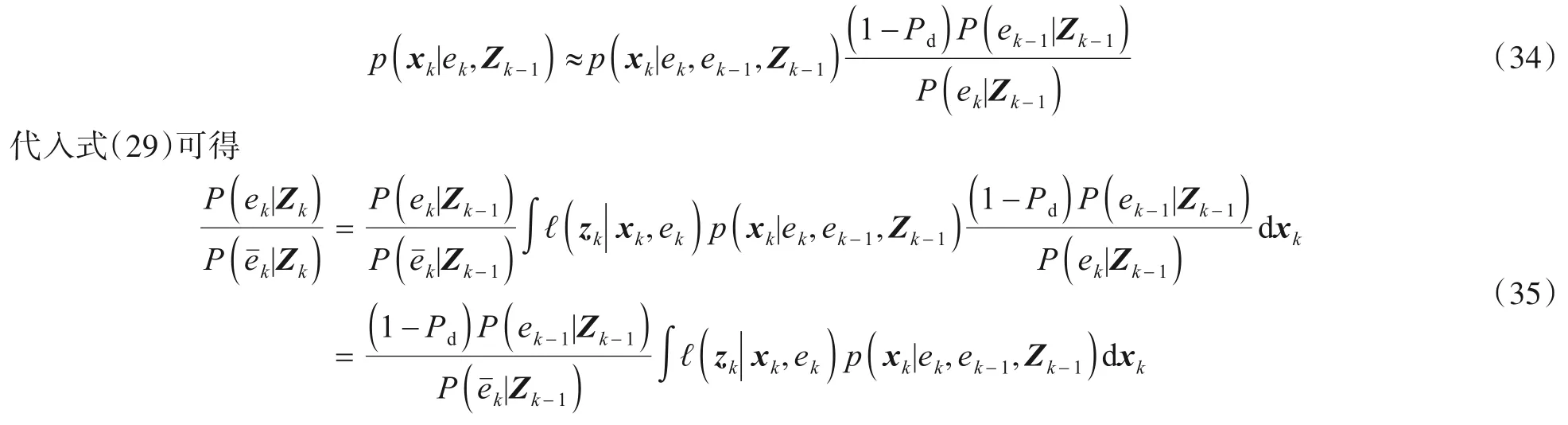
由全概率公式和条件概率乘法定理可知

同样忽略新生密度函数的影响，则有

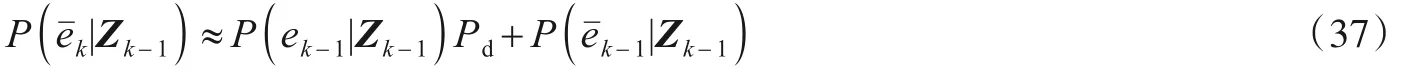
将式（20）和式（37）代入式（35），即可得到后验概率比的表达式：

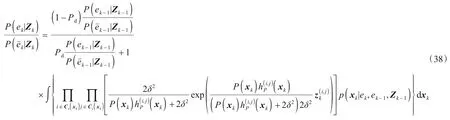
5 检测门限设置方法

5.1 检验统计量的简化模型

用H0表示目标不存在的假设，即Ek=eˉk；用H1表示目标存在的假设，即Ek=ek.选择对数后验概率比作为检验统计量：

其中，Λk为检验统计量，ηk为检测门限.检测门限和虚警概率Pfa之间的关系为

由式（40）可知，检测门限的求取需要利用检验统计量的概率分布，而系统的高度非线性导致无法对其解析计算，针对此问题，首先需对检验统计量进行两个步骤的简化.

第二步，根据Jacobian定理［25，26］，将指数函数累加后求对数运算简化为求最大值运算：

5.2 不存在目标的情况

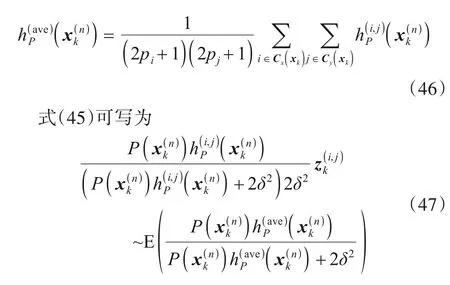
Θ第三项是预测概率密度，由于粒子滤波重采样步骤的作用，粒子群中各粒子的预测概率密度较为平均，可近似认为是常数.

由上述分析可知，在观测区域内不存在目标的情况下，若在粒子群中随机选取一个粒子代入中计算得到ξk，则ξk服从包含位置参数的伽玛分布，分布参数可表示为

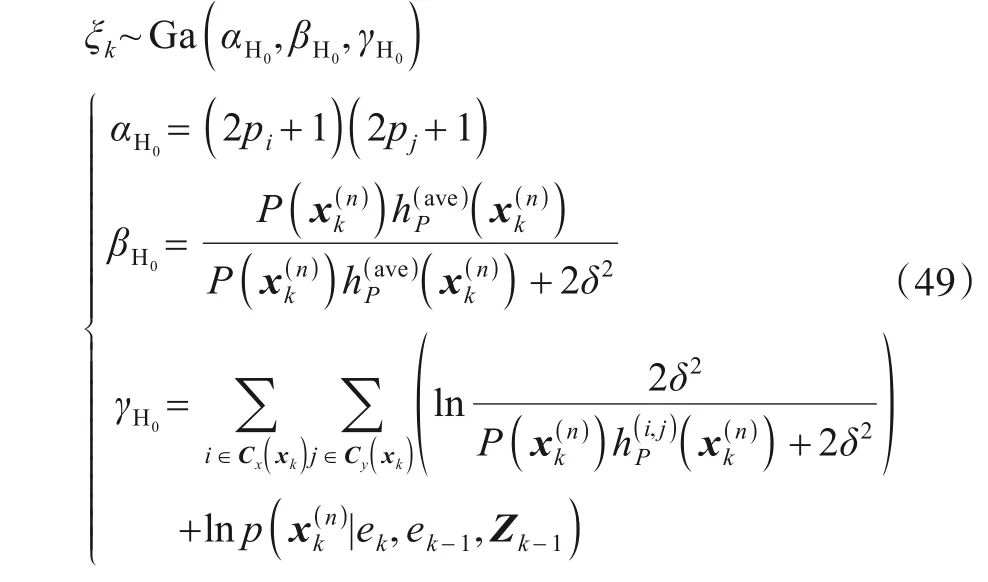
但是，由式（42）可知，在计算检验统计量Λk时并非在粒子群中随机选取粒子代入算式，而是选取了使)最大的粒子，在H0假设下等效于选择了对应的观测区域功率最大的粒子，此时第二项中的不能认为是空间内随机采样，因此不服从指数分布.

针对此问题，对式（42）中的取最大值操作进行近似处理，将集合中元素按降序排列后取较大的前个元素构成子集（Pr为子集占全集的比例，Ns为粒子数），在子集中随机取值，所取的值用εk表示，则检验统计量变为

由于随机变量ξk是在集合中随机抽样得到，随机变量εk是在集合较大元素构成的子集中随机抽样得到，则在ξk的概率密度曲线中截取横坐标较大的部分即可反映εk的概率密度变化趋势.

根据上一时刻的后验概率比，利用式（43）递推地计算Φk，利用式（49）和式（50）计算随机变量ξk的概率分布函数p(ξk|H0)，进而可得p(Φk+ξk|H0)，从中截取横坐标较大的部分可反映p(Φk+εk|H0)变化趋势，即检验统计量的概率密度变化趋势.

设概率密度函数p(Φk+ξk|H0)如图1 所示，将曲线下区域分成A，B，C三部分，若B+C区域对应的概率密度曲线下面积为子集占比，即

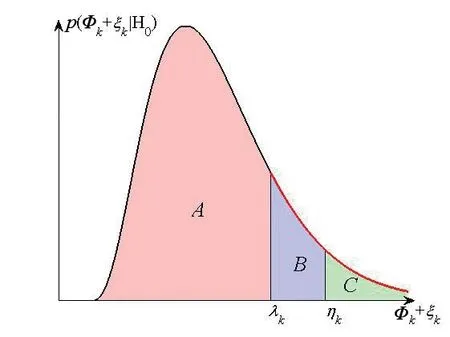
图1 概率密度函数示意图

则B+C区域对应的概率密度曲线（图中红线部分）可反映p(Λk|H0)=p(Φk+εk|H0)的变化趋势.

设B与C区域交界位置横坐标为检测门限，则虚警概率为

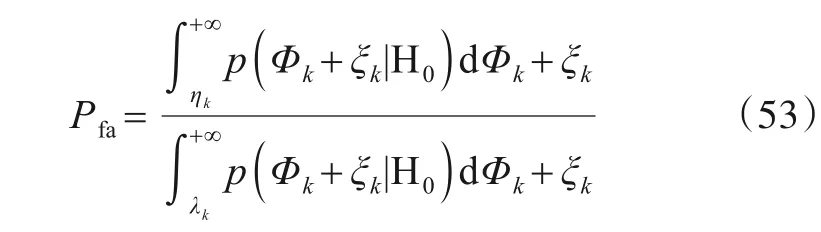
式（52）与式（53）相乘可得

最终可得到检测门限的解析表达式：

5.3 存在目标的情况

观测区域内有目标存在时，由1.2 节分析可知测量值服从指数分布，记为其中xk为真实的目标状态.随着观测时间增加，粒子集中各粒子的状态会逐渐接近目标的真实状态，尤其集合中较大元素构成的子集对应的粒子状态与目标真实状态较为吻合，可认为

1）组织开展年度节能目标责任评价考核。为加强对所属单位节能目标责任的管理，确保所属单位节能目标责任的落实，中国海油将节能计划、节能减排投资计划纳入年度生产计划和预算体系，将节能目标作为约束性指标层层分解到各单位。每年组织专家对所属单位上一年度节能计划完成情况、节能工作开展情况进行评价考核。评价考核结束后，对所属单位的考核结果进行通报，对未完成目标任务的单位，严格实行“一票否决”制度。

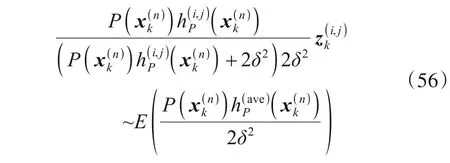
因此，在H1假设下，若利用式（57）所示的伽玛分布参数计算互补累积概率密度函数得到检测门限则理论上检测概率应为PrPfa.但在实际操作中，为控制虚警概率，需利用式（51）所示的伽玛分布参数计算互补累积概率密度函数得到检测门限

式（49）与式（57）之间的差异在于尺度参数，目标线谱信噪比大于0 时，由于伽马分布对尺度参数较为敏感，因此远小于即实际计算的门限远小于使检测概率为PrPfa的门限，使得目标能够以较大概率被检测.目标线谱信噪比越大，相差越大，检测概率越大.

6 仿真试验与结果分析

6.1 仿真场景设置

设被动声纳Lofar 谱的方位观测范围为[0，360]°，方位单元间隔为0.2°，频率观测范围为[150，200]Hz，频率单元间隔为0.1 Hz，观测区域包括1 800×500 个方位-频率观测单元，观测时长1 100 s，观测时间间隔1 s.

在H0假设下，设vI，k和vQ，k的方差δ2为1，利用式（7）至式（9）逐帧在各观测单元加入噪声功率信号，可得到不包含目标的仿真数据.

在H1假设下，设置一种典型的水下目标跟踪场景.设观测区域内存在一个具备线谱特征的目标，观测站航向0°，航速4 kn，目标初始距离7 km，目标初始方位115°，目标航向45°，目标航速6 kn，目标固有线谱频率175 Hz，目标线谱信噪比10 dB.根据相对态势计算目标方位变化情况，根据相对运动速度计算受多普勒效应影响的线谱频率变化情况，结果如图2所示.

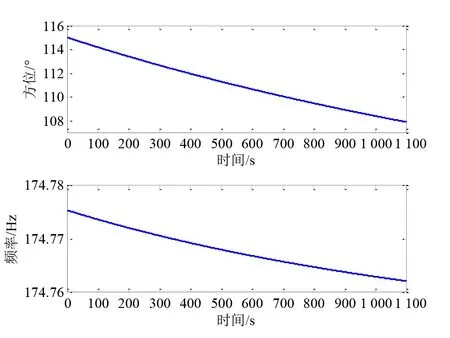
图2 方位及频率变化情况

由图中方位变化情况可知，1 100 s 时间内目标方位由115°逐渐减小至107.9°，变化速度较为稳定；由图中频率变化情况可知，1 100 s 时间内目标频率变化幅度小于0.02 Hz.由此可证，构建目标状态模型时对于目标位变率恒定且线谱多普勒频移恒定的假设是合理的.

在对各观测单元加入噪声功率信号的基础上，利用利用式（7）至式（12）逐帧叠加目标功率信号，可得到包含目标的仿真数据，初始时刻目标位置附近的Lofar谱图如图3所示.

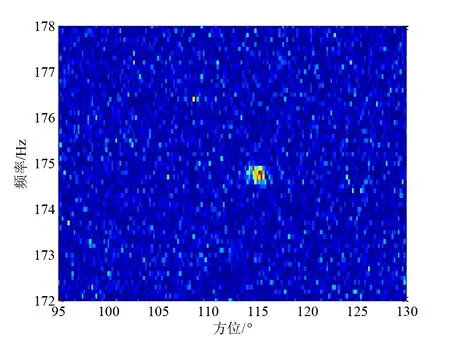
图3 目标位置附近的Lofar谱图

6.2 概率分布情况验证

考虑到水下目标方位变化速度较小，海洋环境的复杂性可能造成线谱信噪比起伏，根据经验将过程噪声协方差矩阵中目标运动状态、目标线谱频率、目标线谱信噪比的过程噪声级分别设置为0.01，0.1，0.1.基于不包含目标的仿真数据，利用粒子滤波TBD 算法对其进行处理，逐帧在粒子群中随机选取一个粒子代入式)中计算得到时间序列ξk，采用矩估计方法［29］计算其分布参数的估计值，利用式（49）计算分布参数的理论值，比较估计值与理论值以验证H0假设下对ξk分布特性的分析是否正确.设邻域参数pi和pj均为1，粒子滤波算法中目标信噪比估计项下限为-10 dB，则分布参数的理论值为分布参数估计值如图4实线所示.

基于包含目标的仿真数据，采用相同的过程噪声协方差矩阵，利用粒子滤波TBD 算法对数据进行处理，设子集占比Pr=0.2，逐帧在集合较大元素组成的子集中随机取值得到时间序列εk，采用矩估计方法［29］计算其分布参数的估计值，利用式（57）计算分布参数的理论值，比较估计值与理论值以验证H1假设下对εk分布特性的分析是否正确.设邻域参数pi和pj均为1，则分布参数的理论值为-26.19，收敛后的分布参数估计值如图4虚线所示.

图4 分布参数估计值

6.3 虚警概率和检测概率验证

基于不包含目标的仿真数据，利用粒子滤波TBD算法进行处理，逐帧计算检验统计量和检测门限，可判决得到虚警概率；基于包含目标的仿真数据，利用粒子滤波TBD 算法进行处理，逐帧计算检验统计量和检测门限，可判决得到对目标的检测概率.设邻域参数pi和pj均为2，子集占比Pr=0.2，系统要求的虚警概率从0.01 到0.1 间隔0.01 变化，对各虚警概率设置情况进行105个采样点的蒙特卡洛仿真，结果如表1所示.

表1 虚警概率及检测概率仿真结果

由表1 可知，对于各虚警概率设置值，虚警概率计算值与设置值之差均小于0.01，检测概率均大于0.95.由此得证，利用本文所提方法可按照系统要求有效控制虚警概率，同时可以实现对目标的检测.

导致虚警概率计算值与设置值存在偏差的主要原因是，利用式（46）对邻域空间内功率分布函数进行取平均值操作，若将邻域参数pi和pj设为0可较大程度地减小偏差，但不利于存在目标情况下对目标的检测.设置的目标线谱信噪比较高，导致计算得到的检测概率较高且浮动范围较小，因此并未出现传统ROC曲线中检测概率随虚警概率增加而增加的趋势.

7 海试数据运用

海试数据来源于某次综合性水声试验，探测装备为被动拖线阵声纳，目标为具备线谱特征的合作声源.数据时长1 200 s，初始时刻目标相对观测站的方位为314°，目标与观测站间距离为8.9 km，观测站以5.5 kn航速、88°航向匀速直行，目标以7.7 kn 航速、241°航向匀速直行，观测站和目标航迹如图5所示，经、纬度坐标刻度的整数部分用字母替代显示.

图5 观测站和目标航迹

初始时刻的实测Lofar 谱如图6 所示，图6（a）中目标方位、频率对应的观测单元位于虚线圆中，将目标所在的局部区域放大显示如图6（b）.

由于被动拖线阵声纳存在左右舷模糊现象，因此图6（a）以观测站航向为轴左右对称.由图6（b）可知，目标方位、频率对应的观测单元及其相邻方位观测单元能量较强，原因是单帧处理利用的时间长度内目标方位发生变化.

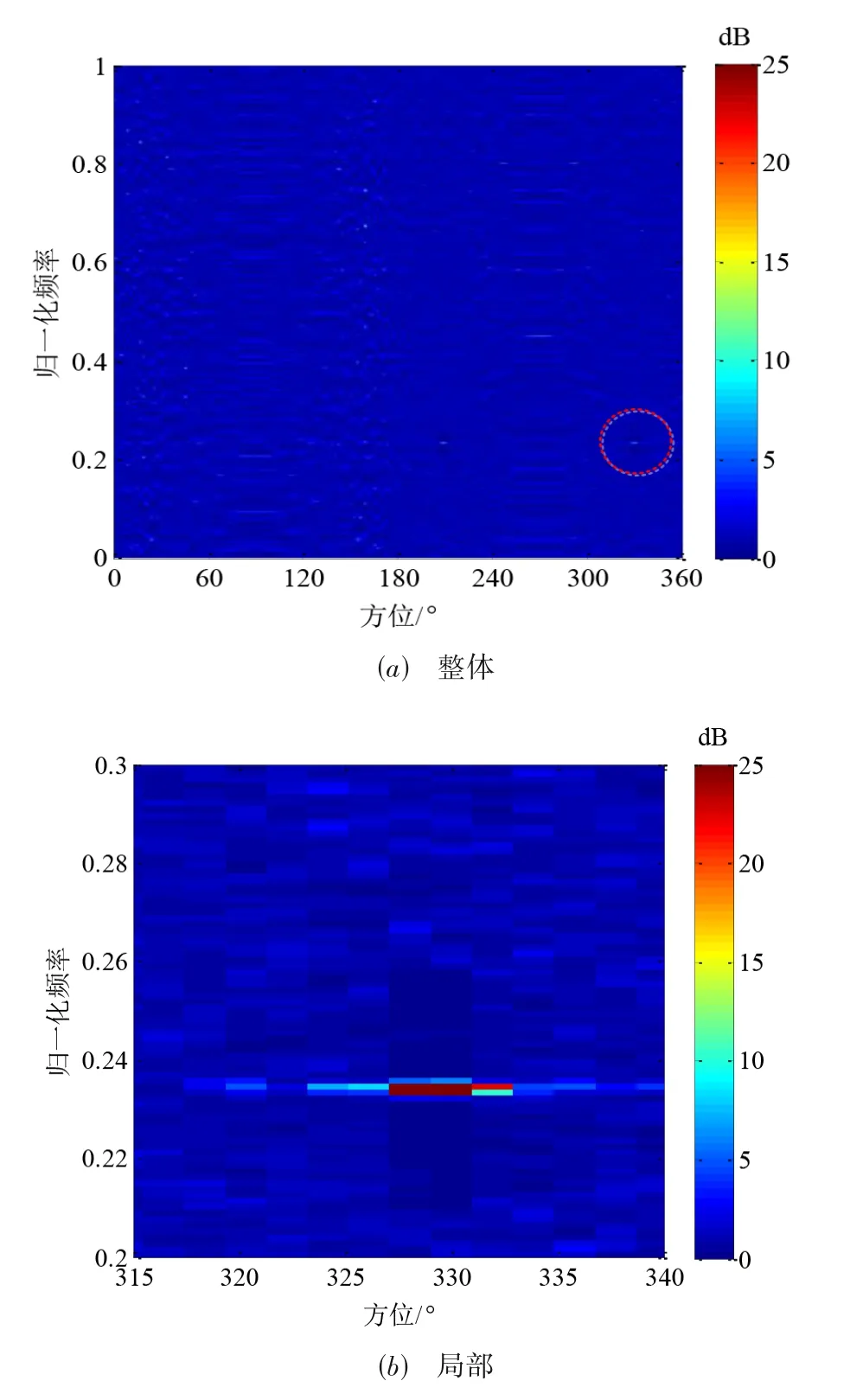
图6 初始时刻Lofar谱实测结果

本文在被动声纳观测量满足指数分布的前提下开展研究，下面利用海上实测数据对此进行验证.逐帧在FRAZ 谱上目标所在位置取值，得到目标能量观测序列；在FRAZ 谱上不受目标影响的区域取值，得到噪声能量观测序列.由于每帧仅取得一个目标能量观测数据，但可以取得多个噪声能量观测数据，因此噪声能量观测序列长度远大于目标能量观测序列长度.

满足指数分布序列的数学期望等于指数分布参数（率参数）的倒数，因此可通过计算观测序列的期望得到率参数.根据率参数可计算观测序列满足指数分布假设下分布函数的理论值，直接对观测序列进行统计分析可得到实际的分布函数经验值，分别对目标能量观测序列和噪声能量观测序列进行处理，结果如图7所示.

由图7可知，目标能量和噪声能量在指数分布假设下的分布函数理论值与基于海上实测数据的分布函数经验值较为接近，可初步判断其服从指数分布，与1.2节理论分析结论和文献［24］观点一致.由于目标能量观测数据有限，因此图7（a）目标能量分布函数的经验曲线不甚光滑.

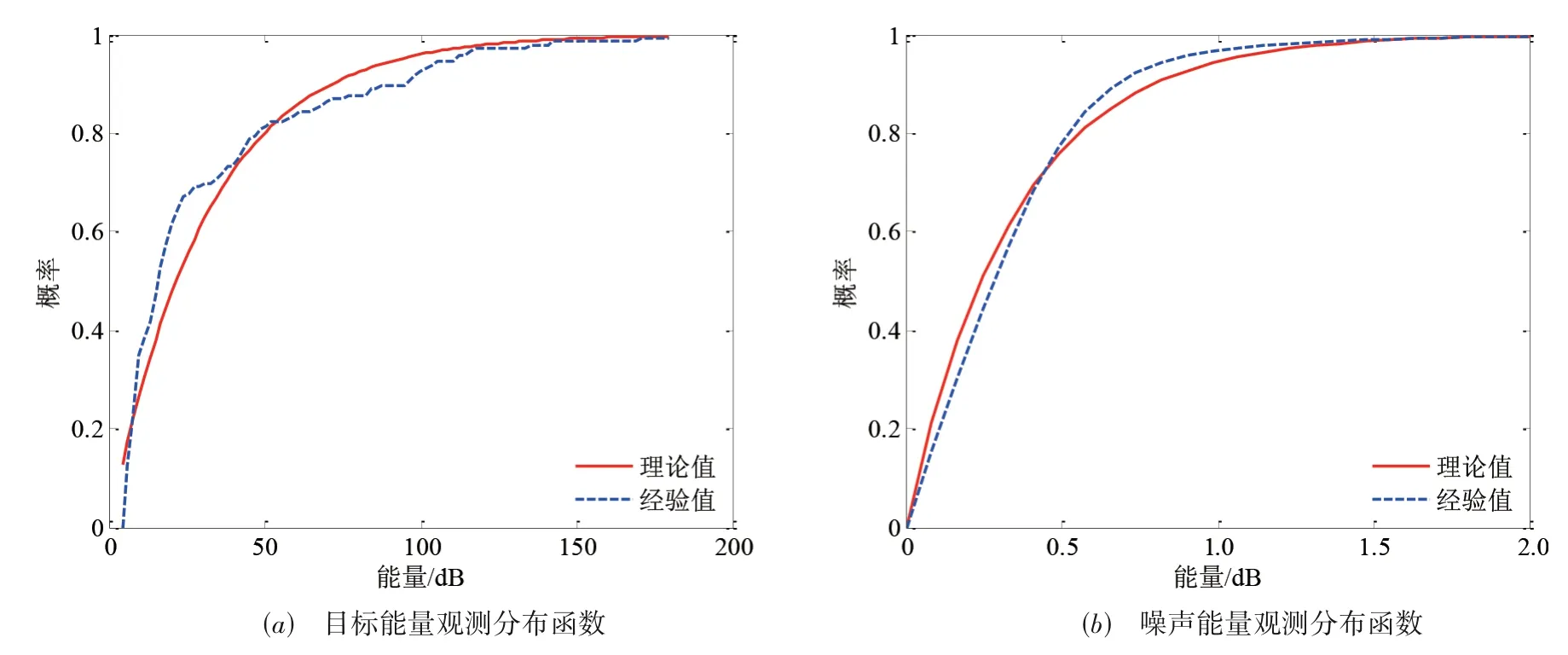
图7 分布函数对比

基于海上实测数据，利用粒子滤波TBD 算法进行处理，逐帧计算检验统计量和检测门限，根据检测结果和真实目标位置可得虚警概率和检测概率.设邻域参数pi和pj均为2，子集占比Pr=0.2，系统要求的虚警概率从0.01 到0.1 间隔0.01 变化，对各虚警概率设置情况进行105个采样点的蒙特卡洛计算，结果如表2所示.

由表2 可知，对于各虚警概率设置值，虚警概率计算值与设置值的平均偏差为0.006 2，检测概率均大于0.9，本文所提方法的可行性和有效性得证.导致海试数据处理结果劣于仿真试验结果的主要原因是，检测门限设置算法假设Lofar 谱观测噪声功率恒定，而海洋环境复杂性导致实际的Lofar 谱观测噪声功率存在起伏.

表2 虚警概率及检测概率计算结果

8 结论

为了按照系统要求的虚警概率设置检测门限，本文针对粒子滤波检测前跟踪算法，在被动声纳观测量满足指数分布的情况下，设置对数后验概率比为检验统计量并对其进行简化，详细推导了检验统计量与系统虚警概率之间的关系，给出了检测门限的闭式解.蒙特卡洛仿真结果表明，利用所提的门限设置方法得到的虚警概率与系统要求的虚警概率之间偏差小于0.01，检测概率大于0.95.本文方法有效地控制了虚警概率并能够实现对目标的检测，海上试验数据进一步验证了算法的可行性和有效性.

所提方法的应用不局限于被动声纳Lofar 谱，同样适用于测量值满足指数分布的其他情况.由于门限计算过程中存在多次近似处理，因此实际虚警概率与要求虚警概率之间存在一定偏差，下一步应着力于减小此偏差.