基于弯曲声线和测距修正的水下节点定位算法

陈嘉兴，程 杰，董云玲，刘志华

（1.河北师范大学计算机与网络空间安全学院,河北石家庄 050024；2.河北师范大学河北省网络与信息安全重点实验室,河北石家庄 050024；3.河北师范大学河北省供应链大数据分析与数据安全工程研究中心,河北石家庄 050024；4.河北正定师范高等专科学校,河北石家庄 050800）

1 引言

近年来，水下无线传感器网络（Underwater Wireless Sensor Networks，UWSNs）受到国内外学者的广泛关注［1］.UWSNs作为无线传感器网络（Wireless Sensor Networks，WSNs）的延伸，用来获取监测水域的实时信息.其中，位置信息对某些UWSNs的应用场景至关重要，如环境监测、海洋采样、灾害预防等［2］.因此，UWSNs的节点定位技术颇具研究意义.然而，GPS（Global Positioning System）难以为水下节点提供位置参考［3］.因此，需要通过节点部署、路径规划等方法赋予一部分节点精确的位置信息，以便为其他节点提供位置参考，通常称其为参考节点，而其余节点称为未知节点，需根据参考节点估计自身位置［4，5］.

由于水下参考节点位置难以获得且易受水流影响，所以参考节点的部署策略、位置获取是UWSNs定位的首要难题［6］.此外，UWSNs的声波通信方式使其通信时延远大于WSNs［7］.因此，UWSNs 中基于时间的测距方法如到达时间（Time of Arrival，ToA）的精度也会有所下降；由于介质分层导致的声线（声信号传播轨迹）弯曲的影响，基于到达角度（Angle of Arrival，AoA）的UWSNs定位算法需重新设计［8］.

综上，UWSNs 定位算法应考虑以下方面：（1）因参考节点位置不精确导致的定位误差［9］；（2）因水下声信号传播特性及传感器精度导致的测量误差［10］；（3）因障碍物对信号反射导致的测量误差.

为降低因参考节点位置不精确导致的定位误差，文献［10］采用了自上而下的定位思路，将带有GPS 的参考节点布置在水面，逐层定位水下节点.文献［7］推导了度量翻转歧义的节点置信度用以优化自上而下的定位框架，有效降低了累积误差.其他针对参考节点位置不确定性的优化方案有基于射线方程的最大似然法［6］和基于测量过程的状态演化模型［11］.为了降低由于水下声信号传播特性及传感器精度导致的测量误差，文献［12］构建了适用于弯曲声线的ToA 测距误差和有效声速的映射关系.文献［8］在噪声分布和声线已知的前提下提出了一种适用于弯曲声线的ToA 补偿技术.为了降低障碍物对信号反射导致的非视距路径测距误差，文献［13］提出了两步加权最小二乘定位策略.文献［14］在两步最小二乘的基础上构造了概率分布函数来降低非视距路径的影响.其他非视距路径优化方案有高斯混合模型［15］、半定规划［16］.

然而，在UWSNs 中需同时考虑弯曲声线和障碍物对测距影响.此时，沿用视距路径与非视距路径对两种测距情况进行描述并不恰当.因此，下文将使用理想路径和非理想路径描述上述两种情况.

为了降低非理想路径及声线弯曲对测距的影响，本文提出了一种抛物模型PMRL（Parabolic Model Ranging Localization）定位算法.

2 模型与假设

针对水下参考节点位置的不确定性，本文在自上而下定位框架［10］的基础上，将参考节点同时部署在水面和水下.此外，假设水下的普通节点和障碍物随机分布，如图1所示.

在图1所示的模型中，仅有水面参考节点能够通过GPS实时获取自身位置，而水下参考节点通过与水面参考节点通信获得自身位置，水下普通节点则通过与水下参考节点通信获得自身位置.因此水下参考节点需具备较强的通信能力.此外，为了降低由于误差累积引起的定位误差，将置信度η［10］大于95%的已定位的普通节点升级为参考节点，其中η由式（1）算得.

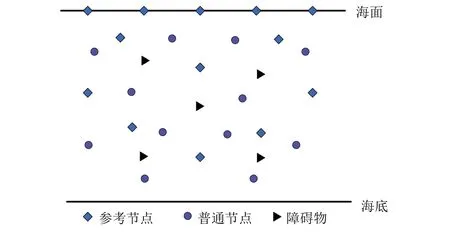
图1 节点分布模型

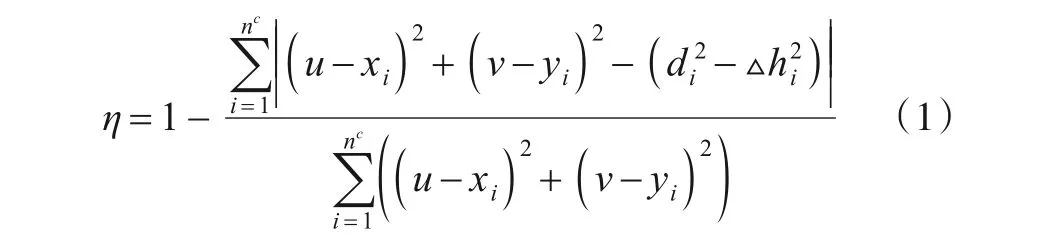
其中，△hi=|w-zi|为普通节点U与参考节点Ci之间的深度差.(u，v，w)为节点U的坐标，(xi，yi，zi)为能与U通信的第i(i=1，2，…，nc)个参考节点Ci的坐标，nc为能与节点U通信的参考节点的数量.di为普通节点U与参考节点Ci之间距离的测量值.

基于上述模型，PMRL 算法需要对水下参考节点和普通节点进行定位.由于两种节点的定位过程在算法思路上没有区别.因此，下文中将使用参考节点和未知节点对上述两种情况进行统一阐述.

3 PMRL算法

PMRL 算法结合AoA 和压力传感器得到了抛物模型测距法，然后结合ToA 得到了非理想路径判别阈值和测距优化公式的系数的计算方法.

3.1 抛物模型测距法

根据文献［12］，水下声速为仅与水深h相关的函数v(h).这与声速分层效应［8］相吻合，即在竖直方向声速变化较大.因此，该过程可类比抛物运动模型，假设水平方向声速不变.

设参考节点C在t1时刻广播自身位置，未知节点U在t2时刻接收到节点C的信息.当声信号从深度为hC的节点C到达深度为hU的节点U时，可利用AoA 测得此时声信号的传播速度vU与z轴夹角为α且α∈[0，π 2]，则声信号在水平、竖直方向上的速度vxy、vz(h)分别为

声信号从节点C到U的所用的时间ΔtCU为

根据积分对称性，不妨设hU＞hC.若仅考虑速度变化而忽略弯曲声线，可用式（5）计算节点C与U之间的距离

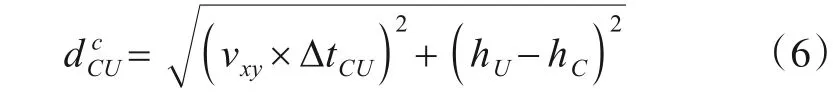
3.2 非理想路径识别

由于障碍物影响，当声信号无法沿理想路径传播时，声信号将沿非理想路径传播.此时，AoA 测得的非理想角度α将导致抛物模型测距法失效.因此，需要对非理想路径下的测距进行识别并剔除.

识别某一测距是否为非理想路径的过程如下：首先利用式（4）计算信号传播时间然后利用可以避免时钟同步的ToA 测量信号传播时间，即节点U在t2时接收到节点C的位置信息后，在t3时刻发送返回信息，而节点C在t4时刻接收到该信息.则为

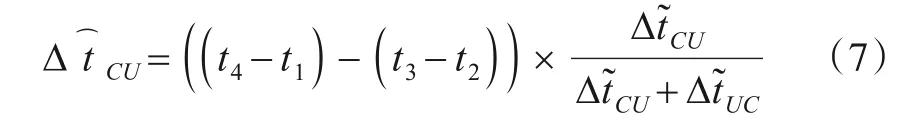
最后计算测量时间与计算时间之间的差值et

若|et|大于阈值μ，则认为该测距为非理想路径测距.

由拉格朗日中值定理得

3.3 测距修正

其中，ΔtCU为信号传播时间真值为信号传播测量时间，ξ为测量噪声，且ξ～N(0，Q).

设信号传播角度真值为α，测量值为，修正值为，修正误差为结合扩展卡尔曼滤波算法得

其中K为系数.K取

3.4 PMRL算法步骤

步骤1 参考节点C实时广播自身位置信息及相应时间戳.

步骤2 未知节点U接收到C广播的信息后，向C发送包含时间戳的确认信息.

步骤3 利用抛物模型测距法计算，利用阈值μ识别并剔除非理想路径测距，并修正剩余测距.

步骤4 利用投影法和最小二乘法完成定位.

4 仿真结果与分析

本文使用Matlab2017b 对算法进行仿真验证，其余仿真参数如表1 所示.由于算法需要实测的深度与声速关系建立水下声速模型，本文利用Origin2019b 和文献［12］中数据v(h)进行拟合，其结果为：

表1 仿真参数表

4.1 参数确定

为了模拟实际测距过程，在深度差和角度α随机的情况下，改变参数计算时间误差如图2 所示.当=0.001 时，时间误差的下降效果最为明显.因此，在接下来的仿真过程中取=0.001.

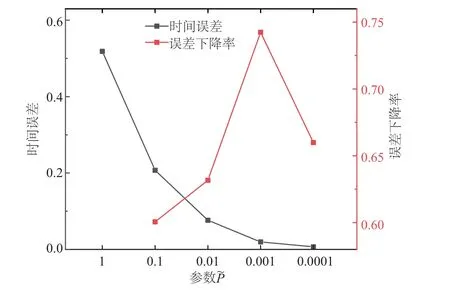
图2 参数与时间误差的关系

4.2 非理想路径测距识别

由于弯曲声线下难以仿真本文算法所需的信号接收角度α，所以必须基于全部测距结果计算一个最大的非理想路径识别阈值用于仿真识别.

图3为参数=0.001，Q随机，其他参数取表1所示参数时，计算去真率、存伪率和识别错误率得到的仿真图.由于识别阈值偏大而导致去真率一直为0 而存伪率较大，从而使识别错误率一直偏大，且随着通信半径增大而不断减小.这是由于随着R增大，其真正的识别阈值与全局最大的非理想路径识别阈值逐渐接近.直至R增大网络区域最大值，去真率达到0.7%，存伪率达到9.6%，识别错误率达到7.7%.此时的非理想路径识别阈值与设定值吻合，识别效果最优.

图3 通信半径与非理想路径识别率的关系

4.3 定位结果

为验证PMRL 算法的有效性，本文设置了以下4 种算法：不考虑弯曲声线和测距修正的SM（Straight sound ray and Measurement）定位算法、仅考虑测距修正的SO（Straight sound ray and Optimization）定位算法、仅考虑弯曲声线的CM（Curved sound ray and Measurement）定位算法和考虑弯曲声线和测距修正的CO（Curved sound ray and Optimization）定位算法.并将文献［10］的CGT 算法和文献［6］的CRLB 算法作为对比算法，取参数=0.001，其他参数如表1所示.

图4为参考节点数（理想路径测距对应的参考节点数）取3 到7，改变参数Q并将CO 算法应用于水下参考节点定位的仿真图.由图4 可知，随着参数Q减小，定位误差逐渐降低但不稳定.这是由于参考节点数不同时，通信范围和参数Q及α使参考节点的测距误差出现了较大差异，弱化了最小二乘法的优化能力.

图4 参考节点数与参数Q对定位误差的影响

图5 为参考节点数取3 到7，参数Q取0.001 得到的仿真图.由图5 可知，提出的测距修正方法对考虑弯曲声线的测距算法和不考虑弯曲声线的测距算法均有效，而且经过测距修正后的算法定位误差更低，定位效果更稳定，这与角度α的误差有关.而CGT 和CRLB 算法不受α的影响，因此定位误差随着参考节点数增加而减少.

图5 参考节点数对定位误差的影响

图6为通信半径取300 m到1 500 m，参数Q取0.001得到的仿真图.由图6 可知，通信半径对CGT、CRLB 算法的影响较小，较SM、SO、CM、CO 算法更为稳定，但SO、CO算法定位误差更低.这表明，提出的测距模型虽然受角度α和深度差的影响而稳定性较差，但通过对角度α修正能有效降低测距误差.

图6 通信半径对定位误差的影响

5 结论

本文构建了水下声速抛物模型，并提出了PMRL定位算法，解决了水下声线弯曲及障碍物干扰引起的定位误差较大的问题.在噪声满足高斯分布的条件下提出了非理想路径测距识别和理想路径测距修正方法.仿真表明，该算法综合性能较好，能够有效地降低定位误差.未来将针对覆盖和节能要求对此类技术进行深入研究.