一种量子条件生成对抗网络算法

刘文杰，赵胶胶，张 颖，葛业波

（1.南京信息工程大学计算机与软件学院,江苏南京 210044；2.数字取证教育部工程研究中心,江苏南京 210044；3.南京信息工程大学自动化学院,江苏南京 210044）

1 引言

生成对抗网络（Generative Adversarial Network，GAN）是一种深度学习模型，是近年来复杂分布上无监督学习最具有应用潜力的方法之一.它由Goodfellow［1］在2014年提出，该模型由生成器和判别器两部分组成.随后，很多学者利用GAN 在图像生成［2］、超分辨［3］、图像转换［4］等领域取得了优异成果，但其过程是不可控的.为了改善上述问题，Mirza 等人［5］提出了条件生成对抗网络（Conditional Generative Adversarial Network，CGAN），在输入层隐变量中增加条件约束引导GAN 从条件分布中采样.2018 年Miyato 等人［6］提出了一种基于投影方法的CGAN算法，将条件约束信息增加到判别器中，提高了数据生成的质量.但CGAN 生成离散数据的效果较差，并且巨大的计算开销可能会使GAN 达到摩尔定律的极限.与经典GAN 相比，量子GAN 可能存在着潜在的指数优势［7］.

量子生成对抗网络（Quantum Generative Adversarial Network，QGAN）是一种基于量子电路［8］的算法.2018年Lloyd等人［9］提出QGAN，从理论角度分析了三种量子对抗学习场景以及QGAN 潜在的量子优势.2019 年Situ 等人［10］提出利用量子玻恩规则生成离散数据，解决了离散数据生成问题.Zeng等人［11］提出了生成对抗量子电路（Generative Adversarial Quantum Circuits，GAQC）算法，利用量子玻恩规则探索量子电路有效采样能力，并利用BAS（Bars-And-Stripes）数据集进行实验验证.由于受限于算法发展和可用的量子资源，先前的QGAN 实验主要针对单量子比特量子态的生成和加载［12］.一些学者关于QGAN 的应用也做了研究［13，14］.但这些算法生成过程具有较大的随机性.Dallaire-Demers 等人［15］提出了一种带有条件约束的QuGAN 算法.该算法加强了对生成数据的控制，但它求解梯度时需要复杂的受控操作和误差纠错，不适合目前的嘈杂中型量子时代.最近，Liu等人［16］提出了一个混合量子-经典条件生成对抗网络算法，该算法提高了生成过程的可控性，但只适合生成经典数据.

为解决这个问题，本文提出了一种量子条件生成对抗网络（Quantum Conditional Generative Adversarial Network，QCGAN）算法.采用one-hot 形式进行多粒子W态编码，使生成器具备根据条件信息生成特定数据的能力.生成器和判别器都由参数化量子电路（Parameterized Quantum Circuit，PQC）构成，前者用来生成拟合训练集的新样本，后者用来判断新样本的真伪以及样本与条件信息是否匹配.该算法适用于经典和量子数据分布学习，降低了时间复杂度且可有效收敛到Nash均衡点.

2 生成对抗网络算法原理

2.1 条件生成对抗网络

针对GAN 训练过程不可控的问题，条件生成对抗网络CGAN 在生成器G 和判别器D 输入中加入条件变量y进行约束和指导.条件变量y可以是任何标签信息，如人脸图像的面部表情、图像的类别等.在CGAN框架下，G 更关注与条件约束密切相关的样本特征，并控制训练过程以生成更高质量的数据.G 的输出可视为从条件分布pG(x|y)中进行采样，因此CGAN 的目标函数为

CGAN 算法需同时对噪声矢量z和条件变量y进行采样，因此为了提高G 拟合真实分布的能力，根据生成目标设置合理的条件变量至关重要.最常见的一种方法是直接从训练数据中选定条件变量，让G和D在接收输入时就得到关于训练集的部分先验知识，此时CGAN可看作是弱监督或有监督模型.

2.2 量子生成对抗网络

尽管CGAN算法在很多领域都表现出优异的性能，但该算法无法直接生成离散数据.而量子生成对抗网络QGAN 算法通过对生成器电路采样可直接生成离散数据，因此吸引了广泛关注.

量子生成对抗网络QGAN 算法流程如图1所示，该算法从原理上也是构造G 和D 的零和博弈.与经典生成对抗网络不同的是，G 和D 都由参数化量子电路PQC构成.量子数据集用密度矩阵表示，对应于经典数据集的协方差矩阵.量子数据集通过量子设备生成，可以直接作为PQC 的输入，而经典数据集需要编码成量子态输入到D 中.在博弈过程中，G 的目标是生成一个量子态迷惑判别器，让其无法判断这个量子态是目标态还是生成态.相反，D 的目标是要区分G 生成的量子态和数据源的目标态.假设G 和D 有足够的能力，这个模型就会收敛到Nash 均衡点，即判别器不能判别输入是真是假.Lloyd 等人［9］指出，利用QGAN 生成高维数据时，对抗性量子博弈学习有潜力以指数级加速收敛到Nash均衡点.

图1 量子生成对抗网络算法示意图

3 一种量子条件生成对抗网络算法

量子生成对抗网络QGAN 算法生成过程具有较大的随机性，本文所提的QCGAN 算法可提高生成过程的可控性，其流程如图2 所示.该算法的G 用来生成拟合训练集的新样本，D用来判断新样本的真伪以及样本与条件信息是否匹配.在数据准备阶段，根据生成任务的目标和数据特征引入条件约束，并将经典条件信息编码为量子态下面对算法过程涉及的关键操作和训练策略进行详细说明.

图2 量子条件生成对抗网络算法框架

3.1 条件信息的W态编码及电路设计

条件信息的W态编码及电路如图3 所示是按照真实样本概率分布将m类条件变量制备成的量子态

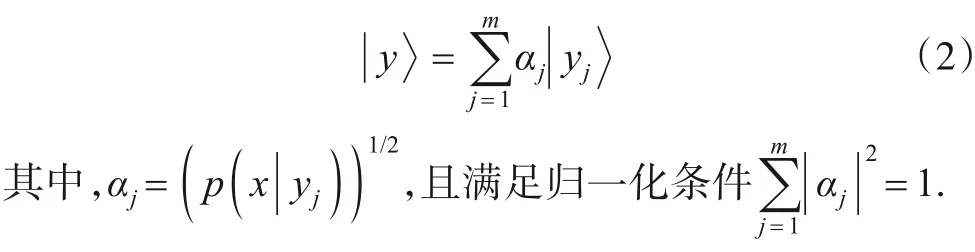
用one-hot 方法对条件信息进行编码.假设待分类种类为m，制备的电路如图3 所示，其中条件寄存器初态为对应的量子位为Q1，Q2，…，Qm.制备过程为：（1）采用Ry和CNOΤ 门，通过调整单量子比特门旋转角度，将量子比特制备成只包含m项的特殊态，即

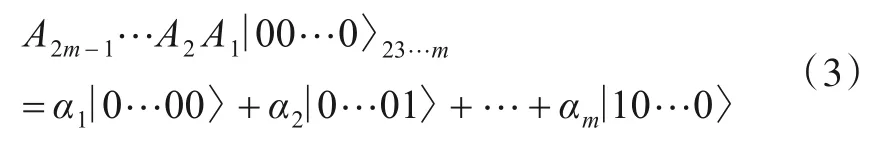
（2）经过图3中的Ⅱ之后，量子态变为

对于企业的内部控制定义，可以解释为：在企业内部，企业的管理层、企业的决策层以及企业内部的全体员工共同参与的，以期实现企业的基本目标的，一系列经营控制活动。而企业的内部控制最主要目的，就是在保证投资者最高利益的基础上，能够创新出更多新型的、价值的内容。其具体实施体现在会计信息的准确性上，根据国家法律法规的规定内容，以及不同地方的政策规定，在使企业的财产和资源更加完整的基础上，实现企业长期发展中的经济效益提升。

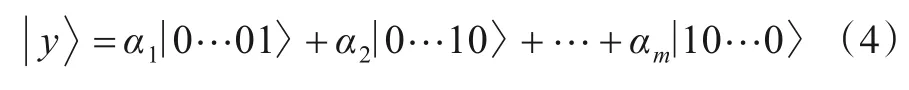
图3 制备m分类的量子电路

采用one-hot 方式对条件信息进行量子态编码，需要用到的量子比特数相对较多，但可减少数据量子/经典后处理时再转换成其他编码形式的工作量.

3.2 量子生成器和量子判别器电路设计

在算法中，G 和D 都由PQC 构成，且PQC 由旋转层和纠缠层作为基础电路模块组成.旋转层可由单量子比特RX、RY和RZ构成，纠缠层可由CNOΤ 门、SWAP 门或CRX、CRY 和CRZ 门组成，其拓扑结构可为：线型、环型、星型和全连接型.

生成器G 电路如图4所示，寄存器对应的量子位用Qj表示，其中j={1，2，…，l}.对G 来说，需要（ll=d+m）个量子位，其中数据寄存器有d个量子位，用来生成样本数据；条件信息寄存器有m个量子位，用来接收m类条件信息.它们的初始态分别为表示制备量子态的电路模块.在电路中，旋转层和纠缠层交替迭代LG次，其中i∈{1，2，…，LG}，θ是G的参数.

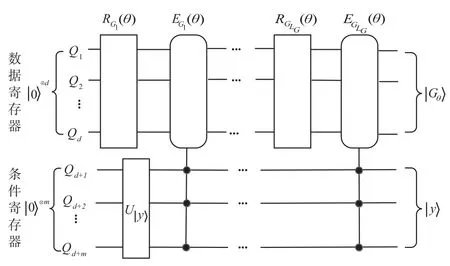
图4 生成器G的量子电路

图5 判别器D的量子电路

用泡利Z测量D 的最终态，其结果为其中i表示量子位索引表示输入到判别器的数据

3.3 对抗训练策略设计

量子条件生成对抗网络的训练是具有反馈回路的参数优化量子算法，生成器和判别器的可训练参数分别记为θ和φ，其目标函数为

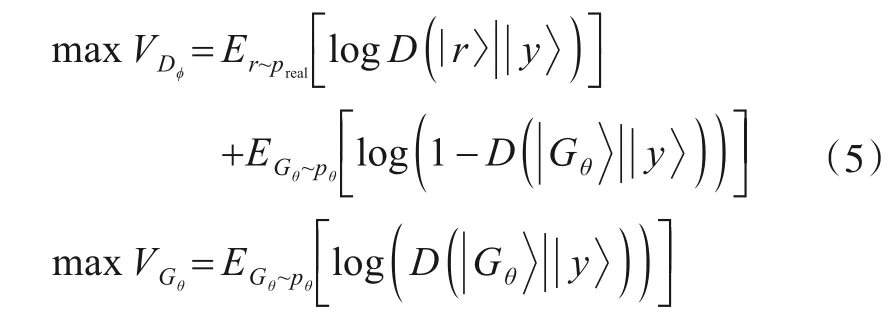
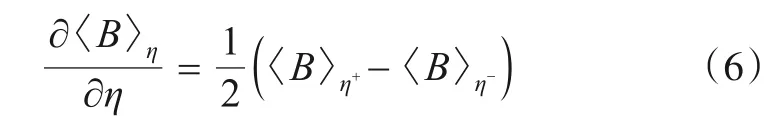
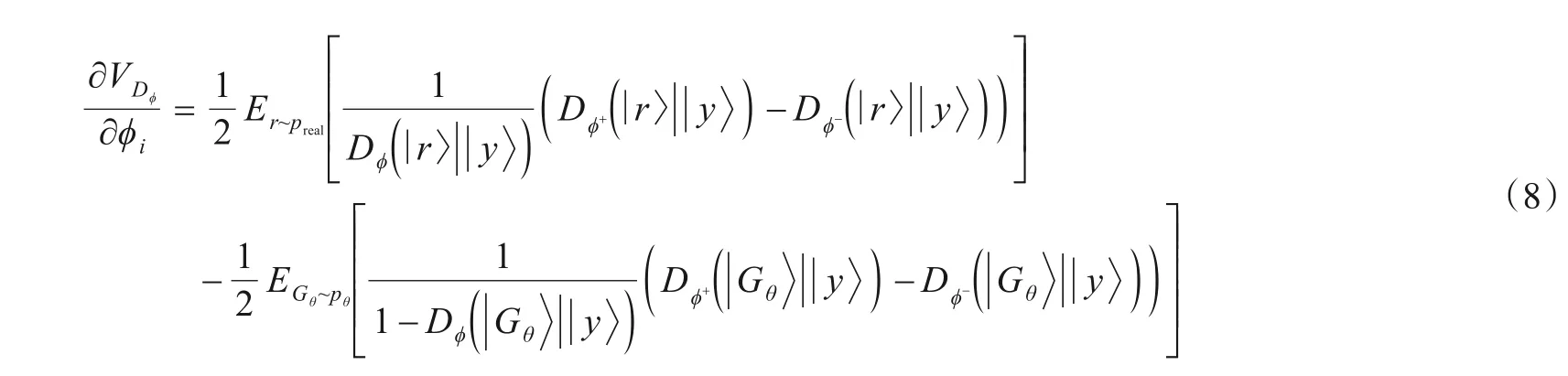
4 性能评析

表1 五种生成对抗网络算法性能对比(生成数据类型中,C表示连续数据,D表示离散数据)

由于损失函数可微性限制，经典算法（GAN、CGAN等）无法直接生成离散数据，而量子QGAN 对电路采样可直接生成离散数据.对于生成N维数据分布，经典GAN 算法时间复杂度为O(N2).而量子信息处理器仅需logN（qubits），其时间复杂度为O(N).

对于GAQC 来说，需要2d（qubits）制备真实数据和量子编码.但其生成过程具有较大的随机性，不太适用于现实场景.对于带条件约束的QuGAN 和QCGAN 算法，G 增加了条件信息的输入，消耗的量子资源也会增加.其中，QuGAN生成器和真实源都需要d（qubits）生成目标数据，m（qubits）表示条件信息和n（qubits）辅助位；判别器需要m（qubits）表示条件信息，s（qubits）辅助位，2（qubits）用来输出判断结果和求解梯度；故QuGAN总资源消耗为2d+3m+2n+s+2（qubits）.而QCGAN 算法的G和D都只需d（qubits）生成目标数据，m（qubits）表示条件信息，故QCGAN 总资源消耗为2d+2m（qubits）.因此，QCGAN比QuGAN算法消耗更少量子资源.

5 实验与分析

本文采用PennyLane 平台进行算法仿真，分别完成经典数据和量子混合态的生成任务.

5.1 经典数据的生成

5.1.1 BAS(Bars-And-Stripes)数据集

与GAQC 算法［11］一样，本文采用BAS 数据集进行模型训练.本实验生成目标是BAS（3，3）图像.训练集中总共有14 种有效模式图且符合均匀分布，这些图像可分为三类：横条纹、竖条纹和全色图（像素值全0或全1），根据one-hot 规则分别标注为：001、010 和100 编码，如图6所示.

图6 BAS(3,3)数据集分类示意图

5.1.2 实验设置

在实验中，训练集均包含6 000 个训练样本.为公平起见，将epoch 均设置为200，迭代训练次数为10，批次大小为600，初始学习率为0.001，衰减率为0.1.另外，利用量子Adam优化器优化G和D.

GAQC 算法不需要条件信息的W态编码及电路设计，因此G 和D 都只需要9（qubits）处理数据的信息，QCGAN 算法除了要处理数据信息，还需要3（qubits）接收条件信息.因此，根据图4和5，QCGAN算法G和D的电路可简化为图8 和9.其中，图8 中是图7 制备的，电路旋转层选用RY门，纠缠层选用环型连接CRY门.它们的电路参数分别为108和36个，且初始值从均匀分布U[0，2π)中随机采样.

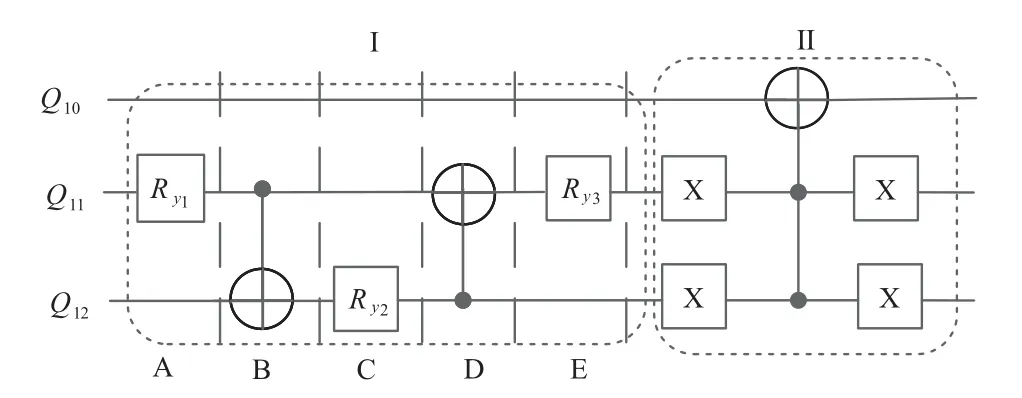
图7 制备三粒子W态的量子电路

图8 生成BAS数据的生成器G的量子电路

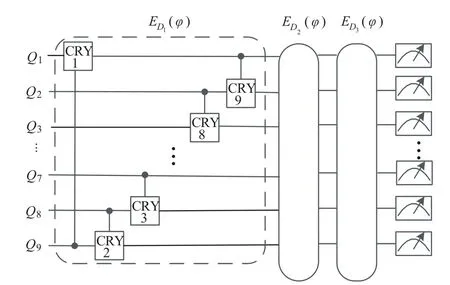
图9 生成BAS数据的判别器D的量子电路

5.1.3 实验结果分析

GAQC 和QCGAN 算法损失函数分别如图10 和11所示.QCGAN 算法在迭代次数为800 时就收敛到了Nash 均衡点，且模型基本趋于稳定.因此，与GAQC 相比，QCGAN生成图像的效率更高.

图10 GAQC算法的损失变化曲线

训练完成后，对G 进行1000 次采样分析生成分布，结果如图12 所示.其中，图12（a）和12（b）分别是GAQC 和QCGAN 算法生成BAS 数据的概率分布，横坐标是用十进制数表示的BAS 数据，轴坐标表示对应的概率值.红线表示目标概率分布，蓝线表示经过训练后G 输出的概率分布.从图12（a）和图12（b）可看出QCGAN 算法生成的数据绝大多数都落在14 种BAS 有效模式图中，且三类条纹图基本符合均匀分布.图12（c）是GAQC 算法生成的前100个像素图，从中可看出GAQC 有两处既没有正确生成横或竖条纹.而如图12（d）所示，可看出QCGAN算法的G 经过训练已具备生成BAS（3，3）数据的能力.

图11 QCGAN算法的损失变化曲线

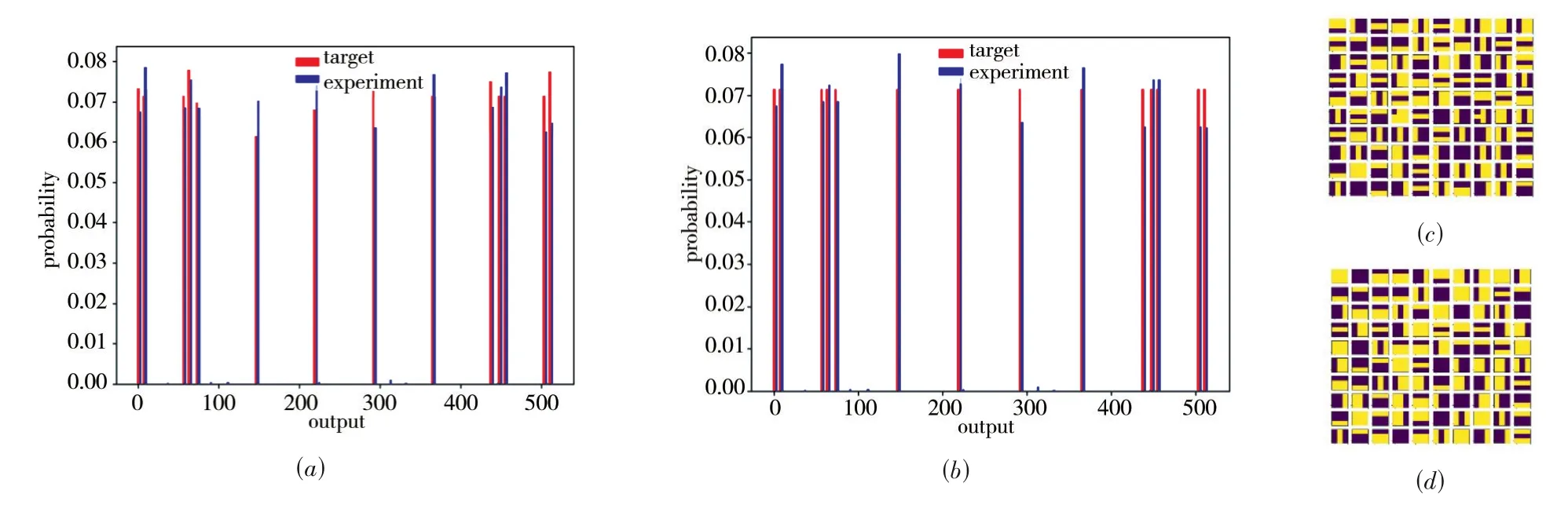
图12 生成BAS(3,3)数据结果

GAQC 与QCGAN 算法生成BAS 数据准确率如表2所示.从表中可看出，QCGAN 算法准确率为0.968 3，而GAQC 算法准确率仅为0.953 2.QCGAN 算法准确率高的原因是该算法加入了条件变量，使模型得到了更多关于真实数据的信息.

表2 算法生成BAS数据集的准确率

5.2 量子数据的生成

5.2.1 实验准备

图13 制备的量子电路

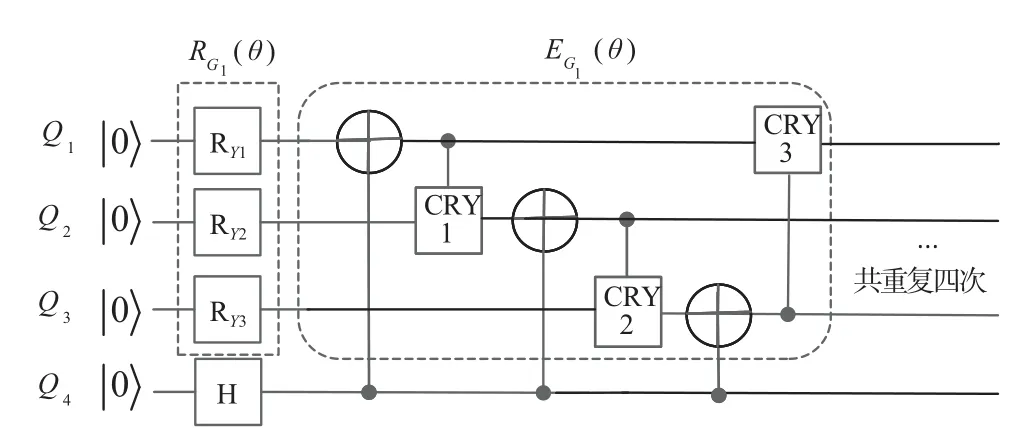
图14 生成量子数据的生成器G的量子电路

将epoch 设置为300，并采用Adam 优化器进行优化.定义表示两个状态的重叠情况，反映了量子电路的保真度.

图15 生成量子数据的判别器D的量子电路

5.2.2 实验结果分析

生成量子数据的损失函数如图16 所示.在迭代次数为500时，生成器和判别器的损失函数已基本收敛到Nash 均衡点，但在后续的训练中G 和D 的损失函数值都出现了轻微的震荡（这是该类算法生成量子数据普遍存在的现象［15］）.

图16 生成量子数据的损失变化曲线

QCGAN 算法生成态和目标态之间的保真度如图17 所示.从图中可看出，通过对抗训练，G 生成的最终态和目标态的保真度逐渐增加并收敛于1，因此该算法能根据输入生成目标量子混合态.

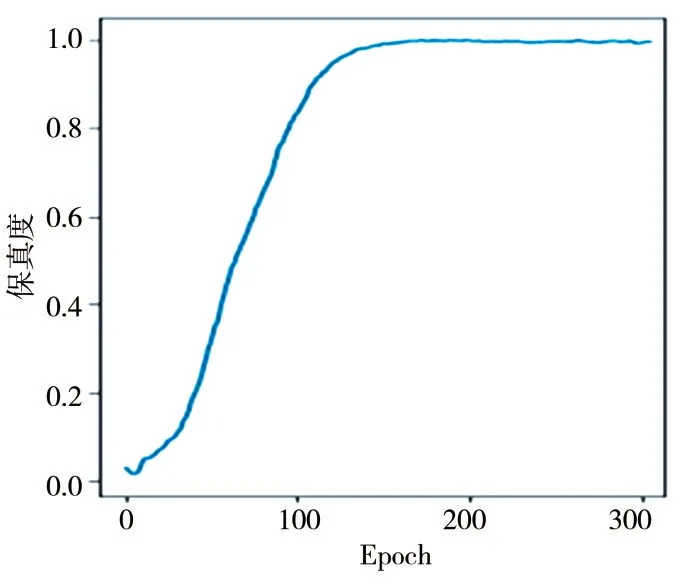
图17 生成量子数据的保真度变化曲线

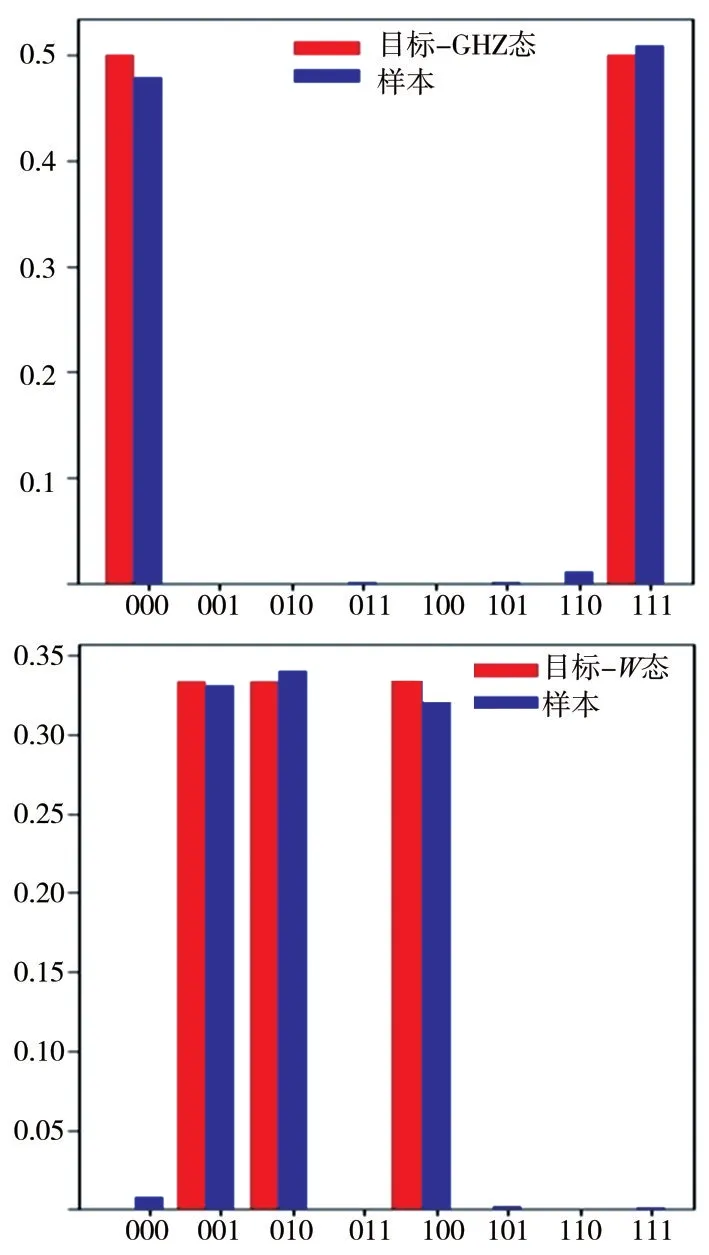
图18 分类生成量子态采样结果

6 总结

本文提出的QCGAN 算法是一种适用于经典和量子数据分布学习的方案.该算法通过在输入层增加条件约束，有效引导网络生成符合特定要求的数据，提高了生成过程的可控性.与经典GAN 相比，本文提出的QCGAN 算法的时间复杂度更低；与QuGAN 相比，QCGAN 消耗更少的量子资源.另外，以BAS（3，3）数据集和量子混合态生成为例，选用PennyLane 进行仿真实验，结果表明QCGAN 算法经过训练可有效收敛到Nash均衡点.

随着问题规模的扩大，算法PQC 中量子位或门数量会急剧上升，容易出现“贫瘠高原”现象（由于运算规模急剧上升，导致电路参数的梯度均值为0、方差随着量子比特个数的增加呈指数减少）.下一步工作，我们将研究通过优化量子电路结构，改进电路参数优化迭代策略等手段，减少一次迭代可训练参数个数和电路深度，从而减轻贫瘠高原的负面影响.