光场相机三维重建研究进展与展望

刘玉轩，张 力，艾海滨，许 彪，孙钰珊，樊仲藜

（中国测绘科学研究院摄影测量与遥感研究所，北京 100036）

1 引言

三维重建一直是摄影测量和计算机视觉的一个基本且重要的问题［1，2］.相比于二维图像，三维模型包含了更加丰富的几何、形状和结构信息，为场景理解与交互提供了更多可能.具体地，三维重建技术是让计算机感知周围的三维环境结构、物体的形状以及物体之间的相对位置等.随着传感器技术的飞速发展，三维重建数据呈现爆炸式增长，三维重建技术也开始更多地走进人们日常生活的方方面面，如自动驾驶［3］、虚拟现实［4］、增强现实［5］、机器人［6］、文物保护［7］、人脸识别［8］和医疗健康［9］等.

目前，研究人员在三维重建领域已经进行了诸多研究.根据所用传感器的不同，主要可分为基于传统影像的三维重建、基于激光点云的三维重建以及基于RGB-D 相机的三维重建.基于传统影像和激光点云的三维重建在理论和实践中都相对成熟，比如基于传统影像的PTAM（Parallel Tracking And Mapping）［10］、Mono-SLAM［11］、ORB-SLAM［12］、ORB-SLAM2［13］和 ORBSLAM3［14］，以及基于激光点云的Cartographer［15］、LOAM（Lidar Odometry And Mapping）［16］、Lio-mapping［17］、hdl_graph_slam［18］、Fast-lio［19］和SuMa++［20］等.基 于RGB-D 相机的三维重建虽然起步稍晚，但也取得许多优秀的成果，比如DVO［21］、KinectFusion［22］、ElasticFusion［23］和BundleFusion［24］、RobustFusion［25］等.尽管这些传感器在室内三维重建中得到越来越广泛的应用，但仍存在一些局限.基于激光点云的三维重建虽然重建精度较高，但是重建出来的三维模型没有纹理信息.单目传感器捕捉真实世界的二维影像，要实现三维重建必须对场景进行多次拍摄构建立体，但由于无法恢复场景的真实尺度，因此得到的只是相对尺度的三维模型.大多数的RGB-D 相机在自然光环境下表现较差，而且量程有限，随着量程的增加，精度会大幅度降低.

近年来，光场相机取得了较大的发展，已经可以做到与传统工业相机差不多的大小，甚至直接集成入手机［26～30］.与传统相机相比，光场相机不仅捕获空间点所有方向光线的累积强度，而且记录了到达某一空间点各个方向光线的强度大小，因此通过一次拍摄获取到多个视角的信息.利用这些多视角信息，可以进行影像重聚焦、增大影像的景深以及评估场景的深度，且不易受外界环境的影响，为三维重建提供了新的可靠数据源.图1（a）给出了单张光场影像的深度估计结果［31］，图1（b）则给出了利用多次拍摄光场影像恢复的包含绝对尺度的大场景半稠密三维模型［32］.

图1 光场三维重建示例

高精度的光场相机三维重建不仅促进了传统三维技术的发展，而且推动了与光场相关领域技术的进步，比如光场超分重建［33，34］、光场显著性检测［35］、光场分割［36］、光场分类与识别［37］和光场拼接［38］等.然而，由于光场相机的内部结构以及光场数据本身的特殊性，基于光场相机的三维重建依然存在较多问题［39，40］.首先，光场相机的内部结构完全不同于传统相机，导致其投影模型和相机畸变模型有别于传统相机.其次，因为光场相机同时捕捉了空间中光线的方向和位置，所以一个空间点会在原始光场数据中成像多次，给光场相机的标定带来了难度.最后，单次拍摄的光场数据，多视角的子孔径图像间的基线较短，传统的多视匹配算法应用于单次拍摄光场数据时效果较差.

针对以上问题，国内外在光场技术方面已经有了较多研究，本文对目前与光场三维重建相关的研究现状和算法，进行了梳理和总结，以期为后续研究人员提供参考和帮助.

2 光场的定义及采集

2.1 光场的概念及二平面表示

光场的概念最早是由Gershun 于1936 年提出［41］，它描述了空间中任意一点在任意方向光线的辐射亮度.为了描述光场，Adelson和Bergaen于1991年提出了全光函数［42］.全光函数包含了光线在空间中的所有基本特性，共7 个维度：光线穿过某一点的坐标(Vx，Vy，Vz)、光线的方向(θ，φ)、光线的波长λ和到达某一点的时间t，可以被定义为

在大多数情况下，处理图像时并不关心获取影像时的绝对时间t.而且，单色传感器仅捕捉在一个较小的波段范围内的光线.在这种情况下，光线独立于波长λ，因此式（1）中的七维函数可以减少为五维P(Vx，Vy，Vz，θ，φ).对于RGB 彩色传感器，可以把3 个波段认为是3个分开的全光函数.

全光函数将光场描述为在空间和时间上连续的函数，但是捕获到的光场仅是整个光场中固定在光线传感器所在区域的部分.虽然有多种方式可以用来表示采集到的光场数据，但其中最简单也最常用的方法是二平面法（Two Plane Parameterization，TPP）［43］.一方面是因为概念上的简单，另一个更重要的原因是它与目前大多数的光场采集设备具有很好的兼容性［44］.光场采集设备的主镜头和传感器是平行的平面，而且图像传感器上的像素是规则排列的，更容易利用TPP 表示光场.图2给出了TPP 的示意图.假设四维光场中一条光线同时穿过2个平行的平面Ω和Π，并且与两平面的交叉点分别为(u，v) ∈Ω和(s，t) ∈Π，则光场L可表示为

利用光线与2 个平行平面的交点可以定义所有光线.图2 中L1、L2和L3是从三维空间中一点O(Vx，Vy，Vz)出的三条光线.假如反射是朗伯体反射，因为是从同一点射出，则L1、L2和L3的亮度值相等.

图2 光场的二平面表示

2.2 光场的采集

传统相机通过叠加各个方向到达同一像素的光线，获得物方点在传感器平面上的二维投影.光场获取设备或方法量测每条光线的位置和方向信息，避免了不同方向光线的积分叠加，从而捕获了每条光线的信息并恢复了设备内的光场.根据构造的不同，当前的光场获取设备主要分为4 类：多传感器捕获［29，45～49］、时序捕获［50～52］、基于掩模［53，54］和基于微透镜阵列（Micro-Lens Array，MLA）［26，38，55～58］的光场相机.图3 给出了几种不同类型光场相机的示意图.表1 给出了当前的主要光场获取方法.

表1 光场获取方法小结

图3 四种典型的光场相机

多传感器光场相机利用分布在平面或球面上的相机阵列同时捕获来自不同视角的光场信息，相机的位置和拍摄的影像分别对应于TPP 中的(u，v)和(s，t).Yang等［45］于2002年利用8×8的视频相机捕捉了动态的光场.同年，斯坦福大学的Wilburn等［46］利用6个CMOS图像传感器来同步记录视频数据获得光场.随后，Wilburn 等［47］构建了如图3（a）所示的相机阵列来捕捉光场.Zhang 和Chen［48］利用6×8 的相机阵列来记录光场，以合成虚拟视角影像，同时通过改变相机位置获得了更好的效果.这些多传感器光场相机体积巨大，为此，Venkataraman 等［29］设计了一个微型的光场相机PiCam.PiCam 包含4×4 的相机阵列，每个相机可以捕捉1 000×750 像素的影像，而且整个相机机身很小，可以集成到手机.Lin 等［49］设计了包含5×5 相机阵列的光场显微镜，专门用于微小场景的拍摄.

与多传感器方法相比，时序捕获方法使用单个图像传感器通过多次曝光捕获不同视角的多个光场样本，典型的方法是使用安装在机械机架上的传感器来测量不同位置的光场，如图3（b）所示.斯坦福大学的计算图形实验室分别利用机械臂和Lego Mindstorms 机械臂［50］按照设计好的路径和位置操作一个传统相机捕获光场.Kim 等［51］按照相同的思路设计了一组仅有一个方向自由度的光场相机，用于室外环境的光场捕捉.Liang 等［52］利用可编码的光圈通过多次曝光来捕捉光场.通过将光圈编码到不透明的纸缝或者液晶阵列中，允许相机记录不同视角的光线亮度，多次曝光并合成不同视角记录的光线信息获得场景的光场.

基于掩模的光场相机通过在主透镜和传感器之间插入可编码的掩模来捕捉光场，如图3（c）所示.Veeraraghavan 等［53］将这种方法称为“Dappled Photography”，相比于直接记录各个方向的光线，利用掩膜对进入相机的光线进行光学调制，后通过傅里叶变换进行光场的重构.得益于学习技术的发展，Marwah 等［54］提出一种基于衰减掩膜的光场相机，利用超完备字典技术从二维投影影像中恢复出光场.

基于微透镜阵列的光场相机是在主透镜和传感器之间放置一个微透镜阵列，将经主透镜后各个方向汇聚的光线重新打散，达到记录四维光场的目的.此时，传感器记录的是通过微透镜的单个方向光线的强度，而不是所有方向光线强度的总和.Adelson 和Wang［55］于1992 年设计了一种新型的单镜头光场相机，可以捕捉5×5 视角的影像.Ng 等［26］通过将一个296×296 的微透镜阵列安装在主镜头和传感器之间，设计了一种手持式光场相机，可以捕捉11×11 个视角的影像.如图4（a）所示，标准型光场相机每一个微透镜位置记录一个空间点信息，而且微透镜的焦距fM等于微透镜阵列和传感器之间的距离B，商业相机Lytro 和Lytro Illum均属于这个范畴［56］.通过调整微透镜阵列与主透镜和传感器的位置，Lumsdaine 和Georgiev［57］提出了聚焦型光场相机.图4 给出了不同模式下聚焦型光场相机主透镜、微透镜、传感器之间的距离关系.如图4（b）所示，如果微透镜阵列安装在主透镜焦平面之前，即fM＜B，这种设计被称为开普勒模式；如图4（c）所示，如果微透镜阵列安装在主透镜焦平面后方，即fM＞B，这种设计被称为伽利略模式.目前，聚焦型的光场相机设计已经被应用到工业光场相机Raytrix［28］.

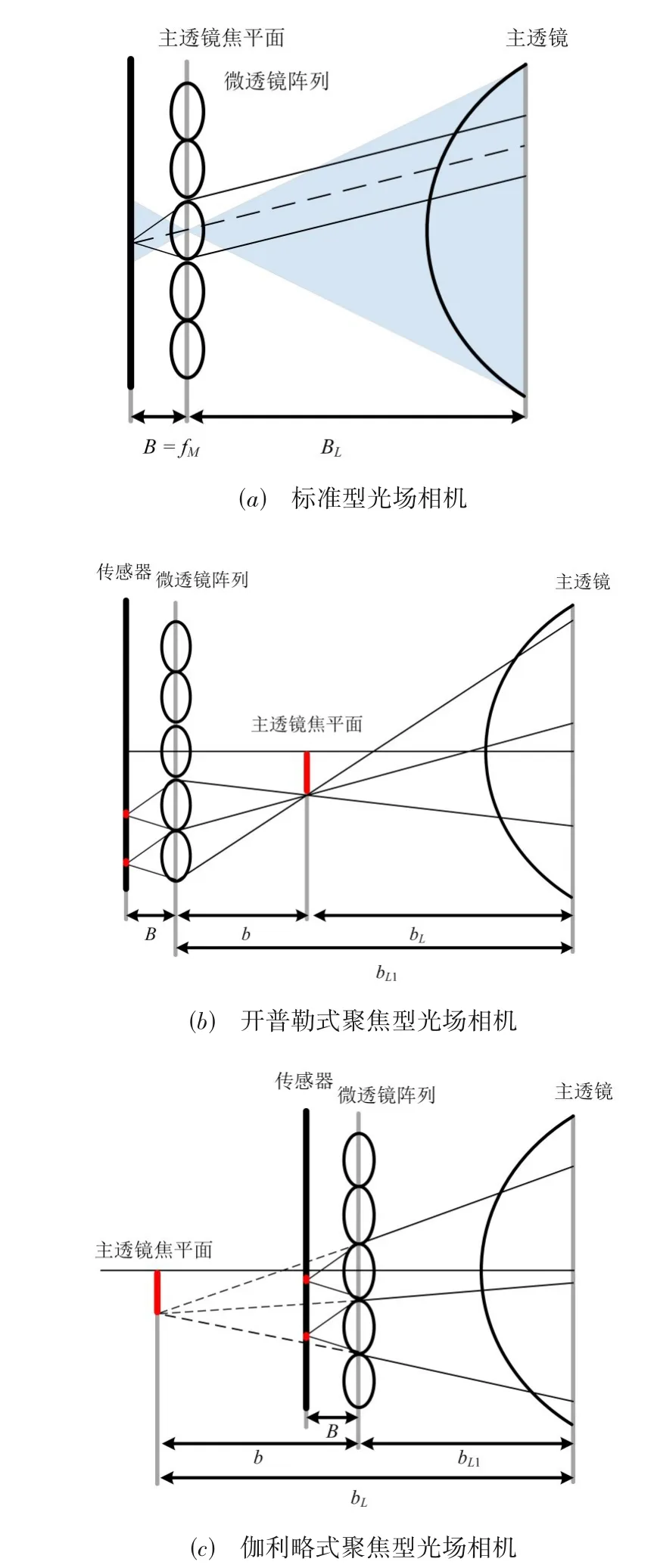
图4 基于微透镜阵列光场相机内部结构示意图

总的来说，多传感器光场相机不需要像基于微透镜阵列的光场相机的特殊光学元器件，但是在同步拍摄、相机标定和图像畸变校正方面存在较大的挑战，而且相机阵列的位置受限于相机的大小.基于时间序列光场相机的方向分辨率则更多是受限于控制它的机械臂的精度，理论上可获得更高的方向分辨率.除此之外，只需对一个相机进行标定.但是基于时间序列的光场相机对装置的精密性要求较高，而且光场数据不是一次拍摄获得，因此更适用于静态场景.对于基于掩膜的光场相机，由于掩膜的透光率无法达到100%，该方式获取的光场数据信噪比较低，目前研究较少.基于微透镜阵列的光场相机体积较小，且能保证同时成像，但利用二维的影像同时记录四维的空间和方向信息，导致空间和角度维度的分辨率权衡问题.除此以外，研究人员仍在研制新型光场相机，比如在Nature Photonics刊登了Shehzad 等［59］提出的石墨烯光场相机，在主镜头后利用多层以石墨烯为材料的传感器来接收不同深度物体的光线，在不损失空间分辨率的情况下，记录了光场.

3 光场相机标定

相机标定指是建立空间中一点与其在影像中对应像素之间的几何关系.不同类型光场相机内部构造不同，一般情况下需采用不同的标定方法.多传感器光场相机和基于时间序列的光场相机可被视为特殊的多视相机阵列，因此可采用传统相机阵列的标定方法.在传统的多视几何标定方法中，多个在不同姿态下的相机被定义为一组无约束的光线，被称为广义相机模型（Generalized Camera Model，GCM）.Pless 等［60］对利用GCM 标定时存在的问题进行了详细的讨论.因此，本文主要关注基于MLA的光场相机的标定.

基于MLA 的光场相机因在传统相机的传感器前方添加了微透镜阵列，导致其投影模型和畸变模型有别于传统相机.而且，光场影像中空间信息和方向信息紧密地耦合在一起，一个物方点会在传感器上多次成像.因此，传统标定算法不适用于基于MLA的光场相机，标定的难度主要在于恢复光线在相机内部的传播路径，包括构建相机投影模型和构建相机畸变模型，并找到光场影像中像素与光线的对应关系.目前，大多将光场相机的主镜头和微透镜阵列的成像模型分别看作薄透镜模型和针孔模型，以此构建完整投影模型，忽略MLA的畸变，在此基础上，采用二维的棋盘格标定板作为物方标定物来确定物方和像方的对应关系.

除此之外，基于MLA 的光场相机记录的光场影像是按一个个微透镜图像排列的，由于微透镜之间的距离不固定且会存在旋转和平移，导致微透镜图像排列不规则.而且，微透镜阵列是按六边形进行排列，以增加传感器的利用率，因此得到的每个微透镜图像也为六边形.为便于后续标定处理，部分方法首先将原始光场影像解码为一组等基线的传统多视影像，并在此基础上进行相机标定；另一类方法则直接在原始光场影像上进行标定.依据标定时是否采用原始光场影像，标定方法可大致分为两类：基于解码后光场影像的标定方法和基于原始光场影像的标定方法.

3.1 基于解码后光场影像的标定方法

为简便地处理原始光场影像，可首先将影像数据解码为一组不同视角的传统二维的子孔径图像.目前常用解码的方法有2种.

一种是Dansereau 等［61］提出的基于微透镜下覆盖像素数目和相邻微透镜之间的几何关系进行解码，进而提取子孔径图像.如图5（a）所示，原始光场影像进行去除马赛克和利用白图像消除衍射影像后，得到的光场数据微透镜图像之间的间距不是整数，且存在旋转.首先对图像进行重采样、旋转和缩放操作使所有微透镜图像中心能够位于像素的中心，结果如图5（b）所示.下一步，根据每个微透镜下的像素数目，把所有像素归类为一个个包含相同像素数、重叠的微透镜图像，如图5（c）和图5（d）所示.其中，(k，l)表示微透镜在微透镜阵列中的坐标位置，(i，j)表示每个微透镜图像内部像素的坐标.上述操作的像素都是在六边形的像素上完成.图5（e）和图5（f）则表示把六边形的像素转化为传统的方形像素以及把长方形像素进一步重采样为正方形像素的过程.至此，得到了解码后的光场数据L(i，j，k，l).

图5 基于微透镜几何关系的原始光场影像解码过程

另一种是Bok 等［62］提出的利用三角构网的方法提取子孔径图像.如图6（a）所示，每个微透镜下距离中心位置相同距离点连接起来构成的三角网，其中红点为每个微透镜图像中心；图6（b）中绿点为目标点像素，每一个绿点都位于对应三角网内部，根据三个角点像素值进行三角网插值可得其像素值.无论哪种解码方法，都需事先找到每个微透镜图像的中心像素，目前通用的做法是利用光场相机的白图像.由于衍射现象，在白图像中，每个微透镜图像中最亮的点就是微透镜的中心.

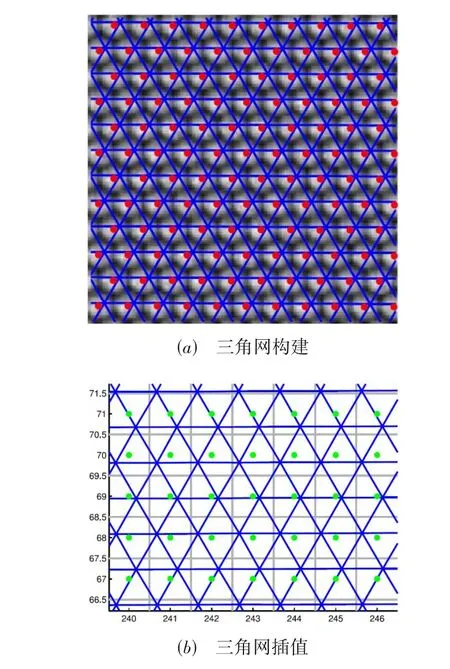
图6 基于三角构网方法的原始光场影像解码[62]

在完成原始光场影像解码的基础上，Dansereau等［61］提出一种包含15个参数的标准型光场相机标定方法.通过构建每个像素与对应光线之间的几何关系，并采用分步求解的方法，完成了标定参数的求解.分步求解过程中，首先基于解码得到的子孔径图像利用传统标定方法得到外方位元素；然后在不考虑畸变的情况下，采用一种线性的方法进行求解，得到所有参数的初值；最后在考虑畸变的情况下，对初始评估结果进行非线性优化.但是求解出的标定参数没有特定的物理现实意义.Zhang 等［63］进一步发现Dansereau 等［61］构建的影像模型中存在参数冗余，提出一种仅包含6个参数的多投影中心标定方法MPC（Multi-Projection-Center）.类比传统GCM 方法，他们推演了光场影像解码出的四维光场与物方三维结构的几何投影关系，实现相机内部和物方世界的MPC 坐标的线性转换.此外，针对该投影模型，他们还提出一种内外方位元素的初始估计方法，通过最小化重投影误差进行非线性优化.与Dansereau 等［61］的方法相比，MPC 具有更少的参数冗余，可同时应用于标准型和聚焦型光场相机.

不同于直接构建物方空间点和像方角点的投影模型，研究人员也通过深度和核线平面影像（Epipolar Plane Image，EPI）等信息间接完成光场相机的标定.Ji等［64］利用光束法平差确定子孔径影像所对应视角在主透镜上的位置，完成了光场相机标定.他们首先找到中心子孔径图像在主透镜上的位置作为参考，其次基于主透镜的焦距估计空间点在不同子孔径图像下得到虚拟像点，最后利用光束法平差求解子孔径图像视角在主透镜上的位置，但该方法的精度受限于方向分辨率的大小.Pertuz等［65］通过构建深度与重聚焦参数之间的对应关系完成了光场相机的标定.对应关系的建立是基于对光场相机成像过程的一阶光学分析推导得到.针对建立的几何模型，提出了一种模型参数求解方法.该方法无需了解光场相机的内部参数，仅需利用传统的棋盘格影像，但该方法只适用于标准型光场相机.Zhou 等［66］通过推演EPI 中线的方向和截距与其对应空间点的三维坐标的投影关系，提出了一种基于核线空间的4 参数几何标定模型.具体地，EPI 中线的方向对应于物方点的深度，水平和垂直方向的截距分别对应于物方点的x和y坐标.该方法利用了更少的参数，但其精度依赖EPI中线的检测精度.

虽然以上方法可以取得相对较好的标定精度，但无论是直接法还是间接法，均未考虑微透镜的畸变，造成一定的精度损失.而且，构建的投影模型相对简单，没有考虑具有不同MLA 结构的光场相机，比如多焦点MLA 光场相机包含几种不同排列的微透镜阵列，因此针对不同类型光场相机构建需设计更全面的投影模型以及畸变模型.

3.2 基于原始光场影像的标定方法

如图7（a）和图7（b）所示，对于棋盘格标定板的原始光场影像，根据每个微透镜图像像素的组成，可将标定板的微透镜图像分为3 类：包含线特征的微透镜图像、包含点特征的微透镜图像和背景类微透镜图像.一些研究人员直接利用原始光场影像的点、线特征来完成相机标定.在几何校正后从原始影像中提取的子孔径图像的质量要优于在解码后光场图像上按照等间距提取的子孔径图像［62］.

由于微透镜图像较小，比如lytro Illum 为15×15 像素，传统的角点检测算法应用于微透镜图像时，精度较差.为此，Liu 等［67，68］提出一种基于原始光场影像角点特征的标定方法.首先，采用2 组模板影像，若待检测点周围的像素分布与模板影像一致，则判定为角点特征，如图7（c）所示.在此基础上，他们将光场相机的固有参数分为与传统相机一致的内参数和光场相机特有的内参数两类，首先对这两部分内参数进行分步求解，再通过最小化重投影误差对初始估计做进一步优化.

图7 光场相机拍摄的原始标定板影像以及提取的点、线特征

如图8所示，当相机与标定板存在较大的姿态变化时，出现大量错误检测和漏检的情况.除此之外，由于优化方法对初始估计不敏感，分步求解难以提高最终精度.针对以上问题，Liu 等［69］提出一种新的基于角点特征的标定方法.首先在原始图像上找到包含角点特征的区域，并提出一种圆形边界策略在这些微透镜图像上检测角点特征；然后基于中心子孔径图像，利用常规标定方法计算初始外参数，并根据角点及其对应中心的几何关系，采用线性方法计算初始内参数；最后，所有的初始估计都通过非线性优化得到进一步的细化.由于提高了角点的检测精度，Liu 等［69］的方法获得了更好的标定结果.针对多焦点聚焦型光场相机标定，Nousias 等［70］同样提出一种基于角点特征的方法.首先，基于聚焦程度区分不同类型微透镜，并将其按照标定板上角点特征所对应点顺序进行排列；其次，通过寻找包含角点特征的微透镜影像中近似沙漏形状两条线的交点确定角点特征的位置；最后，构建空间点与对应角点特征的几何关系，实现多焦距光场相机的标定.

图8 标定板光场影像角点特征检测失败示例[67]

考虑到微透镜影像中包含大量的线性特征，Bok等［62］利用从原始光场图像上直接提取的线特征，提出一种基于原始光场影像线特征的标定方法，实现了光场相机标定.该方法从微透镜图像中利用模板匹配提取直线特征，如图7（d）所示，构建物方与像方的几何投影关系并进行标定参数求解.如图9 所示，从一个物方点PC射出的光线首先穿过主透镜后汇聚于一个虚拟像点PV，PV通过微透镜后投射到传感器上，得到PC在一个微透镜（中心为pc）下的像点p(x，y)；其次，利用得到的几何投影关系计算出初始的内方位参数和外方位参数；最后，通过最小化所提取直线上离微透镜中心最近一点对应的光线与空间中直线之间的距离来进行非线性优化.

图9 标准光场相机投影模型

由于原始光场影像上的线特征较多，算法具有较好的稳定性.但在投影过程中由于非线性项的存在，空间中的直线投影到微透镜影像上时并不是一条严格的直线，因此非线性优化时所选取点对应的光线并不会与空间中的线相交，这会直接影响到标定的精度.此外，微透镜影像中线的检测精度也受限于线检测过程中所选取模板个数的多少.未来可考虑利用点、线特征结合的方法，首先利用大量的线特征提供初值，然后利用角点特征在非线性优化过程中具有的优势，实现光场相机的准确标定.

3.3 典型光场标定方法对比实验分析

本文选定了5种具有代表性的光场相机标定算法，包 括：先解码 后标定 的方法Dansereau 等［61］（记 作DPW），MPC［63］，以及Bok 等［62］、Liu 等［67］和Liu 等［69］提出的基于原始光场影像的标定方法，分别记作BJW，SCC 和LFC.实验数据选用了Dansereau 等［61］提供的5组标准测试数据A、B、C、D 和E（http：//dgd.vision/Tools/LFToolbox/），每组数据中包含多张不同姿态、不同位置拍摄的棋盘格标定板影像.格网的大小也不全相同，其中数据集A 和B、C 和D、E 的格网大小分别为3.61 mm、7.22 mm、35.1 mm.由于原始光场影像上的线特征和点特征只有在相机拍摄失焦的情况下才存在，因此5 组数据中只有部分数据可以用于评估基于原始光场影像的标定方法.具体地，A 组数据中第1、2、4、5、6 幅共5 张影像，B 组数据中第1～5、15～18 幅共9 张影像，D 中第1～15 幅共15 张影像，数据集C 和D 中影 像均在聚焦情况下拍摄，因此均不能使用.每幅图像的大小为3 280×3 280像素，微透镜图像的半径为5像素，考虑到位于边缘视角的子孔径图像会存在比较大的缺陷，仅评价位于内部视角7×7子孔径图像的像方的投影误差（Re-Projection Error，RPE）和物方投影误差（Ray Re-Projection Error，R_RPE）.具体实验过程中，DPW、BJW、SCC 和LFC 利用了原作者提供的最新开源代码，而MPC则直接利用了作者原文中提供的结果.

表2给出了5种光场标定方法的对比实验结果.从结果看出，在数据集A和B上，DPW 和MPC取得了显著优于BJW、SCC 和LFC 的结果，而在数据集E 上，BJW 与DPW 和MPC 的精度在同一水平，LFC 的重投影误差最小.这可能是因为在数据集A 和B 中，基于原始光场影像的标定方法能够利用的有效影像数目明显少于先解码后标定的方法，而在数据集E上，两类方法能够利用的影像数目相差不多，因此两类标定方法的精度相差不多.

表2 几种典型光场标定算法在Dansereau等[61]提供的5组测试数据集上的标定结果

同类方法内，MPC 总体上取得了略优于DPW 的结果，而且由于MPC 的标定参数个数不到DPW 的一半，因此MPC 的标定速度更快.相较于BJW 和LFC，SSC 表现不稳定，在数据集B 上取得了优于BJW 和LFC 的结果，但在数据集E 上大幅差于BJW 和LFC，甚至在数据集A 上标定失败.这是由于SSC 的角点检测方法鲁棒性较差.当标定板所在的世界坐标系与相机坐标系之间的姿态变换较大时，SSC 角点检测失败，进而导致标定失败，在数据集A 上就是这种情况，这也反衬出同样基于原始光场影像角点特征的LFC 的角点检测算法对不同影像姿态具有较好的抗性.除此之外，LFC 的总体表现优于BJW，这是因为最终的优化结果主要取决于非线性优化过程，而空间中的直线投影于二维影像上的过程是非线性的，因此影像上得到的并非严格意义的直线，只是因为微透镜影像较小，可近似看作直线，因此BJW 的表现会差于LFC.需要注意的是，较小的残差输出仅表明在自身算法的优化过程中有较好的收敛，但也可能出现过拟合现象.而且，不同算法的标定参数不同，尤其是基于原始光场影像的直线或者角点特征本身以及数目不同，也会影响到残差计算过程中的公平性.因此，本节仅是对不同光场相机标定方法的初步评估，若要更全面地评估不同方法，需构建更多包含不同条件的数据集，并利用标定的相机参数计算影像深度，并与真实值进行比较.

4 光场影像三维深度信息恢复

光场固有地包含多视角信息，可据此估计场景的深度，但光场结构的特殊性给三维深度信息的恢复带来了挑战，研究人员在这方面做了大量工作.根据光线的不同排列方式，光场有3种可视化表达：多视子孔径图像，角度域影像［71］和EPI［72］.具体地，如果将通过主透镜上同一位置、不同空间位置的光线按空间顺序排列在一起得到一个视角的子孔径图像，而不同视角子孔径图像排列在一起，组成多视角子孔径图像，如图10（a）所示；如果将一个空间点各个视角光线按视角顺序排列在一起，可以得到该空间点的角度域影像，如图10（b）所示；在多视角影像中，如果沿某个方向选择多视角影像并进行前后排列，并沿相同方向取切面，则该切面影像即EPI，如图10（c）所示.基于不同表达形式，当前光场三维深度信息恢复方法分为基于多视匹配［73～75］、基于角度域影像［76～82］和基于EPI［83～89］的光场三维深度恢复.此外，得益于深度学习技术的发展，研究人员也提出诸多基于光场不同可视化表达的利用深度学习进行光场三维信息恢复的方法［90～93］.

图10 光场的三种可视化表达[40]

4.1 基于多视影像的光场三维深度恢复

针对多视角子孔径图像，可利用传统多视的方法来恢复场景的三维信息，但由于不同子孔径图像之间的基线较短，传统的多视角匹配算法性能不佳.为此，Heber 等［73］指出从光场数据提取的子孔径图像与在主动波前采样设置中捕获的图像相似，可以通过测量子孔径图像上图像点旋转密集场的变分模型来计算深度.Yu 等［74］提出一种线辅助的光场三角构网和立体匹配算法.首先将双线性子空间映射到线约束，然后再应用到有约束的Delaunay 三角构网，减少了构网的误差.在此基础上，提出一种线辅助的图割算法，不同视角子孔径图像的线约束下完成匹配，提高了立体匹配的可靠性，但是该算法没有考虑遮挡存在的情况.Jeon 等［75］基于多视的思路提出一种光场深度估计算法.首先利用频域的亚像素偏移，设计了绝对差和梯度差两种数据代价，提高了窄基线子孔径图像的匹配精度，并进一步采用多标签优化模型和迭代优化模型对初始深度图进行优化，但是该方法存在边缘过度平滑的问题.

4.2 基于角度域影像块的光场三维深度恢复

通过重聚焦原始光场图像，可得到一系列具有不同焦距的影像，当聚焦到正确的深度时，角度域影像内的像素会显示出一致性.Tao等［76］提出利用散焦和像素一致性相结合的方法计算深度.他们把角度域影像内像素的方差值作为像素一致性线索，并把重聚焦图像的梯度值作为散焦的线索，然后基于置信度的马尔可夫随机场模型将这两种线索结合起来估计三维深度.在此研究的基础上，Tao等［77］又增加了阴影信息作为正则化，并利用中心孔径图像改进了原始的散焦和像素一致性线索.具体地，以重聚焦图像和中心视角图像的平均强度差作为散焦线索，以包含不同视角的像素块与中心视角像素的差值之和作为像素一致性线索，得到更为准确的深度信息.在未遮挡区域，上述方法取得了比较好的结果，但对于被遮挡像素，如图11 所示，角度域影像内不同视角像素的一致性被破坏，引起估计误差.

图11 在遮挡情况下角度域影像的像素组成

Wang 等［78，79］研究发现，只存在单一遮挡物时，在遮挡区域分割被遮挡视角和未被遮挡视角的直线与空间域中的遮挡边缘具有相同的方向，基于此提出了遮挡自适应的深度估计算法.首先设计了三种遮挡像素检测算子找到被遮挡像素，进而对被遮挡和未被遮挡像素分开处理.具体地，在遮挡区域，仅利用一部分未被遮挡的视角评估深度，提高被遮挡像素的深度评估精度，但该方法仅能应用于存在一个遮挡物的情况.Chen等［80］提出一种基于颜色和空间的双边一致性度量（Bilateral Consistency Metric，BCM），提高了在遮挡区域深度估计的可靠性.BCM 计算了角度域影像中每个视角被遮挡的可能性大小，以此找到不同深度下未被遮挡的视角，并计算代价量.基于不同深度下代价量的变化曲线，确定深度值的可靠性，提高了深度估计的鲁棒性.BCM 虽然在遮挡区域表现较好，但不能应用于方向分辨率较低（比如5×5以下）的光场影像，且对噪声比较敏感.针对存在遮挡和噪声的复杂场景，Williem 等［81］提出了角熵（Angular Entropy，AE）和自适应散焦（Adaptive Defocus，AD）两种数据代价.AE 统计大部分像素亮度的概率，计算不同深度下角度域影像的信息熵，熵值时对应的深度为正确深度.AD 仅测量整个角度域影像中一部分子区域的散焦响应，增强了对遮挡的抵抗性.除此之外，AE 和AD 都添加了额外的颜色相似性约束，获得了较好的深度估计效果.在AE 和AD 的基础上，Williem 等［31］进一步提出了约束角熵代价（Constrained Angular Entropy，CAE）和约束自适应散焦代价（Constrained Adaptive Defocus，CAD）.CAE 基于颜色相似性对每个像素进行加权，而不是赋予所有像素相同的权重，这使得遮挡像素的贡献更小，更好地抑制了噪声.CAD 没有在选定的子区域上添加颜色约束，而是将该约束放置在所有子区域并计算最小代价，降低了遮挡的影响.最后，利用马尔科夫随机场模型（Markov Random Field，MRF）对两种度量进行综合，进一步提高了对遮挡和噪声的鲁棒性，从而提高了在复杂场景下的估计精度.图12给出了BCM和综合利用AE和AD方法在有无噪声情况下恢复得到的深度结果图对比.可以看出，噪声对BCM 方法的影响较大，而后者对噪声具有较好的抵抗性.

图12 在无噪声和有噪声情况下深度估计结果对比

4.3 基于EPI的光场三维深度恢复

EPI中线的方向对应于图像的深度，可通过分析线结构的方向估计深度.Wanner 等［82］使用结构张量计算EPI中线的方向并评估其可靠性，然后使用变分法优化初始深度值，得到亚像素级的精度.该方法从一定的深度范围内直接寻找正确的深度值，而不用将深度范围离散化处理，可得到连续的深度图，而且速度较快，但该方法容易受到噪声和遮挡的影响.Li 等［83］在Wanner等［82］的基础上，增加了颜色一致性约束，提高了结构张量在EPI 上深度估计的可靠性.基于初始估计深度对整幅图像进行分割，并采用稀疏线性系统，在不同区域使用两个不同的相似性矩阵，对初始评估结果进行优化，提高了精度和效率，但依然没有考虑遮挡.Zhang等［84］使用EPI中线上像素的强度、梯度和空间一致性来找到最佳角度，并利用双线性内插提高初始评估角度的连续性.在此基础上，计算每个像素的置信度，找到评估结果不可靠的像素，基于图像本身的结构，将周围可靠像素的深度扩展到不可靠像素，完成整幅图像的深度评估，但是该方法仅能应用于具有较大方向分辨率的光场影像.Suzuki 等［85］针对大视差范围光场数据，提出对EPI 进行斜切处理来提高评估精度.他们发现，结构张量在EPI中线的方向接近垂直时评估精度较高，首先对EPI进行不同程度的斜切处理并计算置信度，然后通过滤波将高置信度的结果集成到最终的视差图中，提高了在大视差情况下的评估精度，但该算法未考虑遮挡.Zhang 等［86］提出了一种基于EPI 的旋转平行四边形算法SPO（Spinning Parallelogram Operator）.SPO 首先通过计算EPI中平行于目标线两侧平行四边形区域的最大加权直方图距离来寻找单方向EPI上的最优方向；然后提出一种可靠的深度置信度评估算法，对水平和垂直方向的评估结果进行聚合；最后利用边缘保持滤波算法进一步优化评估结果.虽然SPO 没有对遮挡和噪声进行明确的处理，但对遮挡和噪声都有较好的抵抗性.

图13 是一张国际棋盘格光场影像［80］.场景中存在复杂的遮挡关系，该种情况下提取的EPI中线结构被破坏（如图中红色和黄色框选区域），导致无法正确提取影像的深度.

图13 EPI在遮挡下的表现[80]

Sheng 等［87］在SPO［86］的基础上，利用多方向的EPI上的有用信息，提高了在遮挡区域的深度估计精度.首先提取多方向的EPI并评估深度，然后利用多次评估的深度值计算两个遮挡线索，找出被遮挡像素.对处于遮挡边缘的像素点，仅利用与遮挡边界方向相同的EPI的评估结果，减少了遮挡的影响.Schilling 等［88］提出一种综合利用深度和遮挡的深度评估模型.具体地，在评估过程中，动态更新已评估像素的深度，以此对待评估像素的各视角信息进行判断，找出未被遮挡视角，计算代价量.在此基础上，利用周围信息进行局部优化.虽然该算法并未进行全局优化，但是在边缘和弱纹理区域均表现较好.

4.4 基于深度学习的光场三维深度恢复

深度学习算法已经在图像处理、目标检测、自动驾驶等领域取得了前所未有的成果.针对光场影像三维深度信息恢复这一问题，研究人员采用深度学习领域前沿算法开展研究，探索深度学习技术在光场三维重建中的应用潜力.Shin 等［89］提出一种基于全卷积神经网络的光场深度估计方法EPINET.首先，利用光场几何特性设计一种端到端的神经网络结构；其次，构建水平、垂直以及左右对角线多流网络；最后，使用16 个光场合成图像，对光场特定数据进行增强，并从这16个合成光场图像中随机抽取23×23 的灰度图像块进行训练.该算法不仅在合成光场数据的各项指标上均表现较好，而且算法的可靠性在一小部分真实光场数据上也得到了验证.为了更充分利用光场影像中有效的多视角信息以及剔除无用信息，Tsai 等［90］提出一种基于新的神经卷积网络光场深度估计算法.首先通过构建视图选择模块生成一幅注意力图，找出每个视角信息的潜在重要性大小，然后利用光场不同视角信息的对称性增强注意力图的对称性，提高了深度估计的准确性，获得了较好的结果.不同尺度和方向的EPI 可能会影响最终的深度估计精度.为此，Zhou 等［91］设计了一种基于EPI的尺度和方向自感知学习方法来估计深度.具体地，以每个像素的多向EPI 块为输入，设计了两种自适应尺度选择和方向融合的网络结构，一种是尺度自感知结构，另一种是用于融合多方向特征的共享权重网络，提高了深度估计的准确性.Wang 等［92］针对光场深度估计，提出一种基于对极几何和图像分割的卷积神经网络.首先利用对极几何来估计初始视差图，然后将多方向EPI 作为输入数据，根据不同方向EPI 的视差选择卷积块，同时利用图像分割结果获得中心视角子孔径图像的边缘信息，通过将两个部分的输出串联起来，得到最终的深度图.

4.5 不同方法对比与分析

不同的数据形式在深度估计中有其自身的优势.传统多视影像可以方便地利用周围信息，但由于影像间基线很短，易出现误匹配，造成错误深度估计.角度域影像能有效地利用光场重聚焦的特点，且易于去除遮挡的影响，但难以利用周围信息.EPI 将视差固定在一个维度，利于提高深度估计的准确性，但当前基于EPI的方法仅利用了线上或者线周围一方面信息，降低了深度估计精度.基于深度学习的方法在部分合成数据上取得了较好的结果，但训练深度神经网络需要非常大的数据集，目前还只有很少一部分包含深度真值的真实光场数据可用于学习，因此基于深度学习的方法还难以应用于真实光场数据的深度估计.

为评估不同方法的性能，本文选用了基于多视的Jeon 等［75］提出的方法（记作MVP），基于角度域图像的Wang 等［78］提出的方法（记作OV）和CAE［31］以及基于EPI 的SPO［86］4 种典型方法进行对比实验分析，其中CAE和OV对遮挡进行了针对性的处理.算法的实现利用了原作者提供的代码，参数按照作者的建议进行设置.实验数据利用了带有真实深度值的合成光场数据和真实光场数据.合成数据是由Wanner等［93］提供的光场数据深度估计算法标准测试数据集中的“Buddha”“Mona”“Stilllife”和“Papillon”数据，便于进行定量评价；真实数据采用了瑞士洛桑理工学院（École Polytechnique Fédérale de Lausanne，EPFL）提供的Lytro Illum 相机拍摄的光场影像［94］.

对于所有的算法，将最大和最小视差范围等分为81个深度标签以确保对于每种算法的每个深度标签的步长是一致的.对于合成光场数据，最大和最小视差的输入是根据真值确定的；对于真实光场数据，最大和最小视差的输入分别取1 和-1.考虑到上述每种方法采用了不同的优化方法，首先比较了未经优化的深度估计结果（Local），以测试每个成本量的区分能力；然后在应用每种算法自身优化方法的情况下，对优化后的结果（Optimized）进行了比较.为了实现定量评估，采用100倍的均方根误差RMSE作为标准.

其中，N是待评估深度图的大小，GΤ 和d分别是真值和计算出来的深度.同时，对被遮挡区域单独评价，用RMSEOCC表示其精度.被遮挡区域根据真值计算得到，具体地，如果真值深度图上某个像素在x和y方向上梯度值和的绝对值大于0.01，则认为该点是被遮挡.

表3 分别给出了几种算法在优化前（Local）和优化后（Optimized）的定量对比实验结果，为方便查看，每组数据的最优结果用加粗标出.MVP 在优化前和优化后均表现不佳.OV 整体表现相对平均，在遮挡区域则表现不稳定，在部分数据上取得了比较好的结果，比如在“Mona”数据优化后深度图的RMSEOCC值为6.457，表现最好，但在“Buddha”数据上优化后深度图的RMSEOCC值为13.238，表现最差.整体上，CAE 在优化前表现最好，在四组数据上均取得了最好的结果，但其在优化后提升有限，仅从0.559 提升到0.429；在遮挡区域，在“Buddha”“Mona”和“Stilllife”数据上则出现了优化后变差的情况，导致其平均RMSEOCC从5.883 变大为7.208.SPO 在优化前均表现较差，但SPO 在优化后有明显提升，比如SPO 优化前RMSE 和RMSEOCC的均值分别为3.491 和8.717，优化后分别提升到0.372 和5.426，在整体和被遮挡区域精度均最高.

表3 几种典型光场深度估计算法在Wanner等[93]提供的合成数据集上的定量实验结果

图14展示了几种算法在合成数据上评估的深度图对比实验结果.可以看出，MVP和SPO的深度图在优化前均存在大量被错误估计的深度噪点，这也是它们在定量结果上表现较差的主要原因.OV和CAE在优化前噪声较少，但OV在边缘出现了明显的错误，CAE则整体表现较好.优化后，MVP 在平坦区域表现良好，但存在边缘过度平滑的情况；OV 在表面和边缘恢复方面表现都比较平均；SPO 和CAE 在细纹理结构和纹理不连续区域都表现较好，同时在纹理匮乏区域均表现较好.

图14 合成光场数据上评估的深度图对比实验结果

图15 展示了几种算法在Lytro Illum 拍摄影像上评估的初始深度图对比结果.数据中不仅包含具有挑战性的场景，例如遮挡、细结构和纹理匮乏区域，而且还存在大量的噪声和失真的情况.从结果可以看出，MVP 在优化前表现较好，但优化后存在过度平滑的问题，且在弱纹理区域出现大片连续区域的错误深度估计.OV 受影像噪声影响较大，优化前存在较多噪声，优化后得到较大程度的提升.CAE 在遮挡边界处表现良好，噪声较少，但在细结构和低纹理区域容易出错.SPO 虽然在优化前的深度图中也存在较多噪点，但考虑到在合成数据中同样存在噪点，因此受光场影像质量影响不大；而且在优化后的深度图上，SPO在保持物体形状、恢复弱纹理表面和保持细结构方面表现最佳.

图15 真实光场数据上可视化对比实验结果

5 开放获取的光场数据和算法

大量的公开光场相机数据以及光场影像处理算法，促进了光场领域的发展.本文对目前的公开资源进行了总结.表4 列出了目前开源的光场数据，包含合成光场影像、多传感器光场影像、基于时间序列的光场影像以及标准型/聚焦型光场影像.斯坦福大学计算图形实验室在光场研究领域非常活跃，先后公布了利用相机阵列、Lego gantry、gantry、光场显微镜、Lytro Illum 拍摄的光场影像，用以深度估计和多次拍摄光场影像的重建性能测试［50，95］.麻省理工学院的Wetzstein［96］、海德堡大学的Wanner等［93］和Honauer等［97］发布了包含真值的合成数据集，用于测试深度估计算法.洛桑理工学院的Rerabek 等［94］、罗马大学的Paudyal 等［98］和慕尼黑工业大学的Hazirbas 等［99］发布了包含不同场景类别和不同数目的Lytro Illum 光场影像数据集.慕尼黑工业大学的Zeller 等［100］公布了利用双目相机和Raytrix R5 同步拍摄的数据，用以对比单目、双目和光场相机在三维重建上的不同表现.法国国家信息与自动化研究所（Institut National de Recherche en Informatique et en Automatique，INRIA）先后发布了Lytro、Lytro Illum、Raytrix R8以及合成光场影像数据集［101］，用以测试深度估计算法、场景识别以及标准型光场相机和聚焦型光场相机的数据联合处理问题.瑞典中部大学的Ahmad等［102］发布了同时包含Lytro Illum 和Raytrix R29影像的数据集，用于测试标准型和聚焦型光场影像的匹配结果.英国的贝德福特大学的Hahne等［103］公布了自主研发光场相机拍摄的光场数据.

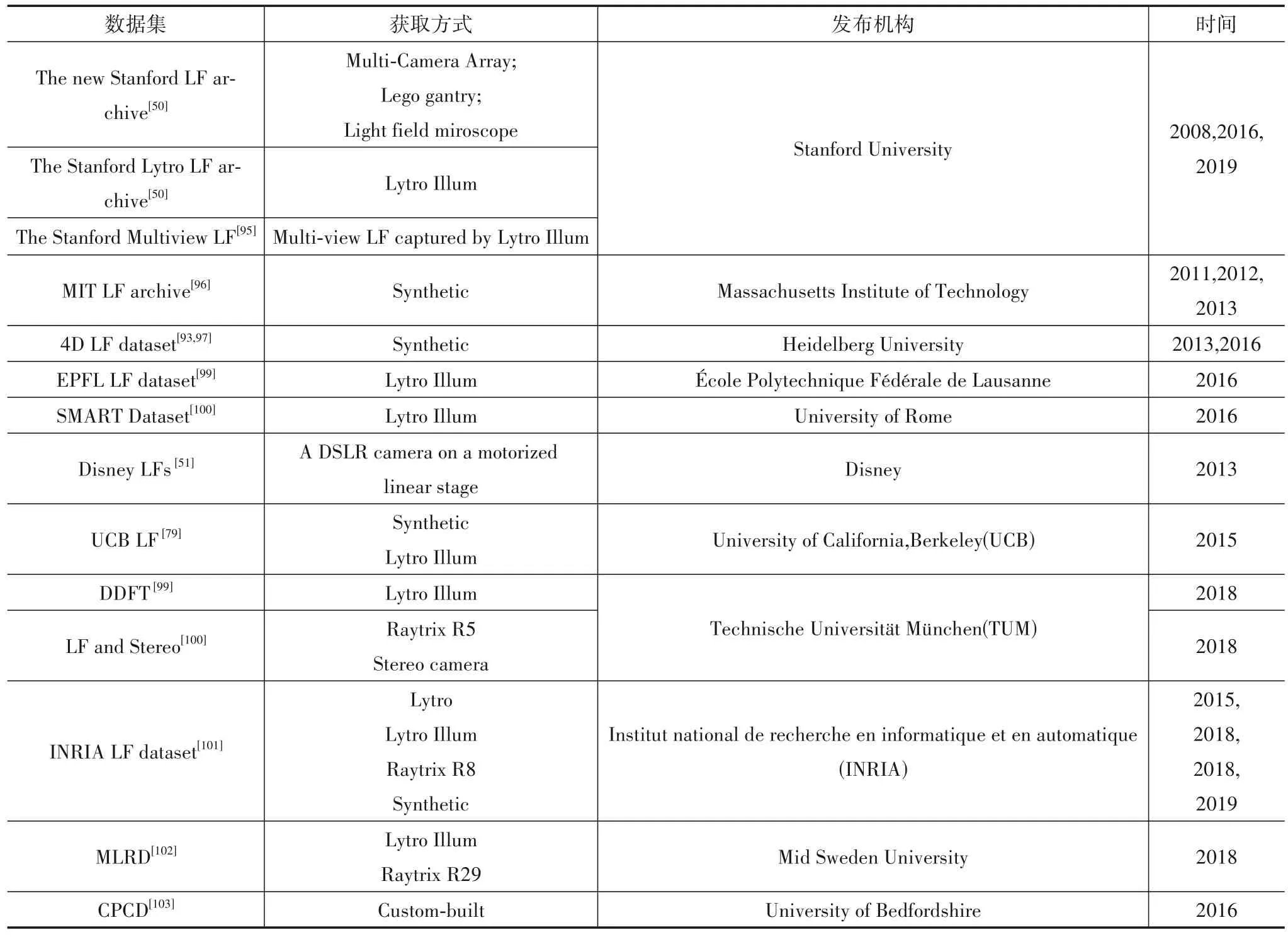
表4 公开的光场数据小结

表5列出了目前与光场三维重建相关的开源算法，包括光场相机的标定和光场影像三维深度恢复两个方面.其中大部分是国外机构开源，另外也有部分国内机构如海军航空大学、西北工业大学和台湾大学等，大大促进了该领域的发展.

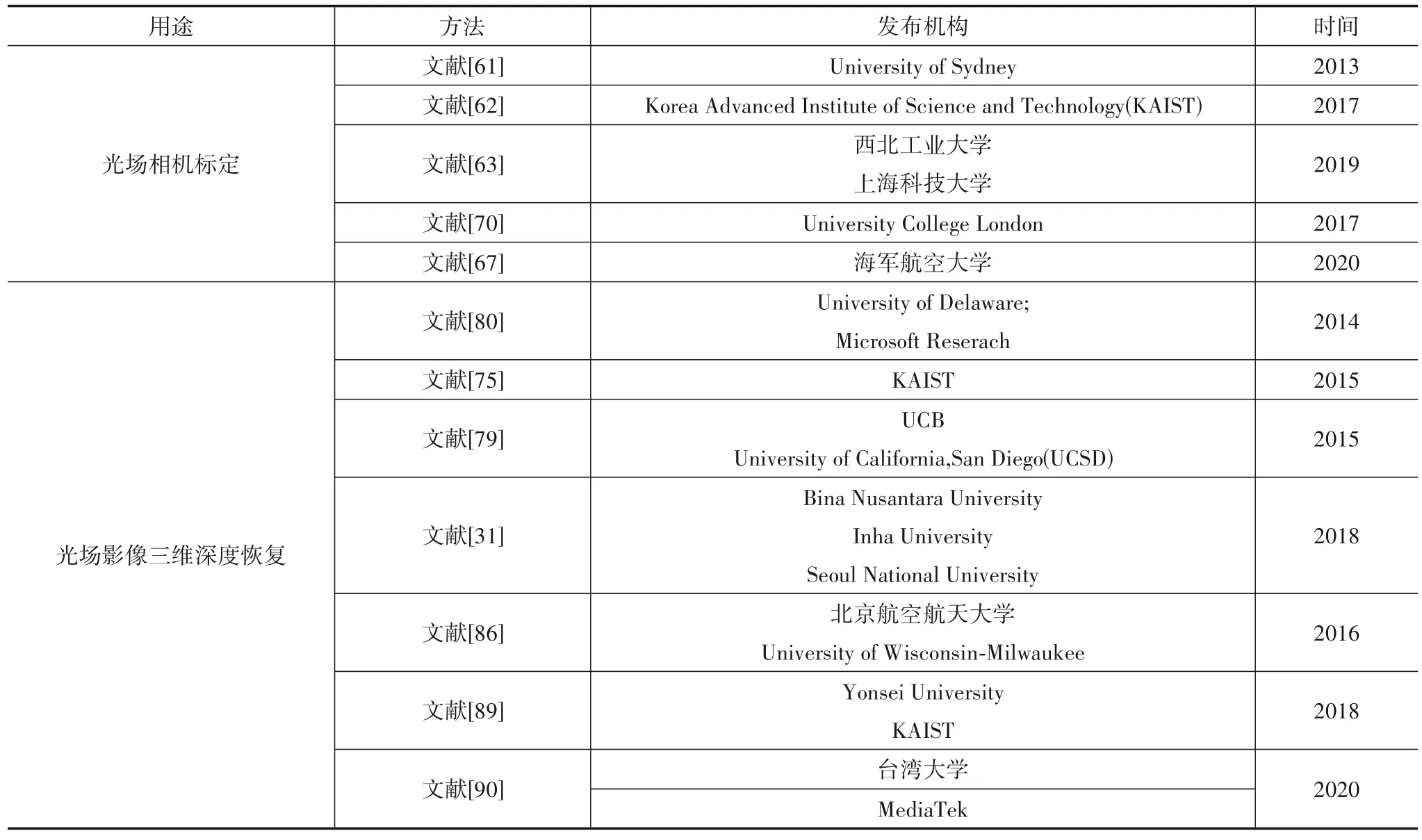
表5 与光场三维重建相关的开源算法小结

6 总结

光场相机作为一种新型相机，能够通过单次拍摄同时采集空间和方向信息，为三维重建提供了新的数据源.目前，光场相机的三维重建研究处于探索阶段，一些基本问题还尚未被解决.为挖掘光场相机的应用潜力，本文对国内外围绕光场相机的三维重建展开的诸多研究工作进行了梳理和总结，并指出了目前存在的主要问题和未来可能的研究方向.

（1）当前的光场相机多为国外生产，迫切需要研制自主可控的国产光场相机.由于空间分辨率和方向分辨率的相互矛盾，相机参数的制定过程中应根据应用进行专业化设计，在提高方向分辨率的同时，保证空间分辨率不会明显下降，并提高拍照速度.

（2）新型光场相机的出现必然会给相机标定引入新的问题，而准确有效地完成相机标定是进行下一步工作的基础.为得到准确通用的标定模型，构建投影模型时需考虑不同内部设计的光场相机并兼顾不同镜头的相机畸变.同时，在标定完成后，需构建大量不同条件的光场影像数据集，对标定算法进行全面而深入的评估.

（3）光场影像固有地包含多视角信息，可用以评估影像的深度.虽然部分深度估计算法在大多数区域都能取得较好的效果，但在遮挡的区域表现较差.为了去除遮挡的影响，其中一个极端是构建同时考虑所有视角遮挡和深度的完全遮挡评估模型，但该方法效率较低.另一个极端是，利用某种策略预先估计被遮挡视角，并利用剩下未被遮挡的视角来评估深度.目前大部分的方法都是基于第二种策略，该类方法难以保证剔除的视角都是被遮挡的视角，被错误剔除的视角信息就损失了，在后续的优化过程中，这些被错误剔除的信息也没有被应用到.因此，在评估过程以及优化过程，从整体和局部同时考虑遮挡是未来的主要研究方向.此外，基于学习的三维深度恢复方法表现出巨大的潜力.

总体来说，光场相机给三维重建提供新的思路的同时，也引入了诸多问题.如何准确地恢复相机内部的光场，实现场景的精细化三维重建在未来的一段时间依然会是研究的热点问题，还需要更进一步地深入研究.