密集杂波背景下雷达微弱海面目标的修正Hough变换TBD检测新方法
包中华,卢建斌,田永华,田树森
(1.海军工程大学电子工程学院,湖北武汉 430033;2.航天科工集团二院二十三所,北京 100854)
1 引言
检测前跟踪(Track Before Detect,TBD)技术是目前公认的较为有效的雷达微弱海面目标探测方法之一[1,2].根据技术途径的不同,TBD 目标检测可通过三维匹配滤波[3]、Hough 变换[4~6]、动态规划[7,8]和粒子滤波[9,10]等多种方法实现.其中,基于Hough 变换的TBD检测方法(Hough Transform TBD,HT-TBD)[11,12]较早被提出并受到广泛关注,其主要优势是对点迹丢失和非均匀采样不敏感,且无需目标数量先验信息.
现代对海观测雷达面临海尖峰杂波的严重挑战.为检测海面低可观测性目标,通常需要设置较低的初级检测器门限,海尖峰杂波能够轻易越过这些门限,由此使得HT-TBD 检测器处于密集杂波点迹环境之中.在密集杂波点迹环境下,传统HT-TBD 检测器性能恶化严重,原因在于:作为一种批处理算法,传统HT-TBD 检测器忽略了点迹间的时序关系,导致检测结果出现大量虚假航迹或剩余杂波点迹.不少学者都已注意到该问题并提出了相应的改进方法.一类改进思路是通过引入速度约束对观测点迹进行筛选,具体实现方法有2种:一是直接使用速度约束预先对所有点迹进行筛选[13],该方法具有理论最优的检测性能和杂波抑制效果,但是计算量巨大,尤其在密集杂波背景下计算量更会出现爆炸性增长;二是使用随机Hough 变换[14]通过随机抽取不同时刻点迹并引入速度约束进行点迹筛选,该方法能在一定程度上对杂波点迹进行抑制,但密集杂波环境下随机抽取到满足约束条件杂波点迹的概率显著上升,而抽取到目标点迹的概率明显降低,算法性能恶化严重.另一类改进思路是使用航迹回溯或航迹检验[15,16],在传统HT-TBD 目标检测基础上,对所有疑似航迹进行检验或回溯处理,以鉴别真假航迹和剔除残存杂波点,该方法在密集杂波背景下同样会因疑似航迹数量剧增(且绝大部分为虚假航迹)而难以工程实现.
本文提出一种基于修正Hough 变换的微弱雷达目标TBD检测新方法.其主要创新在于:一是在传统两级HT-TBD 检测器基础上,增加点迹筛选环节,提出一种基于单帧观测数据的修正单帧Hough 变换(Modified Single Hough Transform,MSHT),并在MSHT 参数空间引入连续多帧共线和速度约束条件,实现对密集杂波点迹的筛选,可在节省计算量的同时最大程度剔除杂波点迹;二是在目标检测与航迹恢复环节,针对海面同时多目标检测的需要,改进经典批处理HT-TBD 算法,使观测数据原点自适应于筛选后有效点迹数据集,得到数据匹配(批处理)Hough 变换算法(Data-Matched Hough Transform,DMHT),可提高参数空间的多目标分辨与检测能力.
2 经典HT-TBD目标检测方法
经典Hough 变换将观测空间中的点(x,y)映射为(ρ,θ)参数空间中的曲线,即
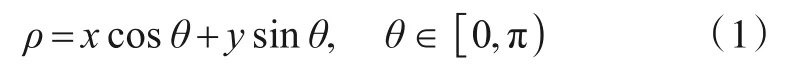
传统HT-TBD 算法的基本流程可参考文献[11],通过参数空间离散化、Hough变换映射与非相参积累实现对近似直线运动目标的检测与航迹提取.
为降低计算复杂度,Carlson 从雷达目标检测的实际出发,改进地提出具有两级检测器结构的经典HTTBD检测器:首先使用较低门限CFAR 检测器和点迹提取器对原始观测进行预检测,以抑制噪声并获得凝聚后疑似点迹集;在此基础上再运用经典Hough变换完成积累检测和航迹提取,以抑制虚警并获得目标航迹.
3 修正HT-TBD目标检测新方法
本文所提基于修正Hough 变换的TBD 目标检测(Modified HT-TBD,MHT-TBD)新方法,其原理如图1所示.
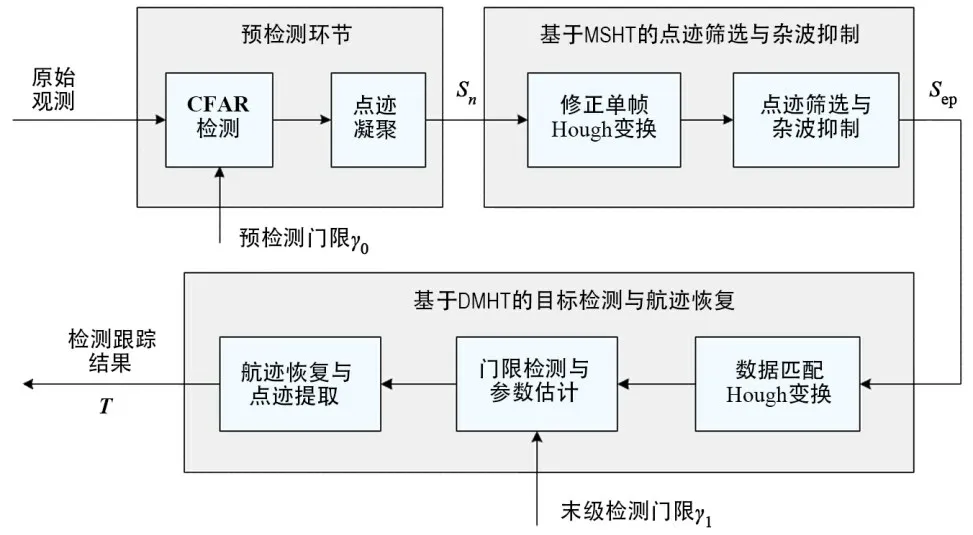
图1 MHT-TBD方法原理框图
采用三级检测器结构,首先对原始观测进行预检测,预检测器和传统HT-TBD 检测器相同,不再赘述;在此基础上,首先进行点迹筛选与杂波抑制,然后基于筛选后点迹数据进行目标检测与航迹恢复处理.
3.1 点迹筛选与杂波抑制
(1)修正单帧Hough变换
假设当前观测数据来自雷达第n次扫描,预检测器输出初步检测结果,记为

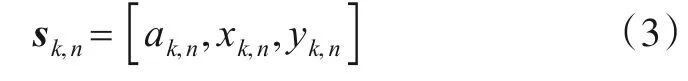
其中,ak,n为幅度;xk,n和yk,n为观测空间水平坐标,不失一般性,仅考虑两坐标雷达情况.
为有效利用时序信息和便于引入多帧共线与速度约束条件,首先逐帧对Sn中所有疑似点迹进行MSHT变换,得到n时刻的MSHT 变换矩阵,记为Hn.所定义MSHT 变换是指在式(1)所示标准Hough 变换基础上,对参数空间积累规则进行修改,具体可描述为

当Hn(ρ,θ)≠0 时,基于算法1 恢复其对应共线点迹的集合算法中FL[•]表示向下取整.

(2)多帧滑窗点迹筛选
令滑窗周期为M(M≥3)帧,考虑目标较杂波更有可能在连续M次观测中保持点迹共线,且相邻周期位置移动受到最大可能运动速度限制,引入连续多帧共线和最大速度约束条件对预检测点迹进行筛选.
①首先在滑窗期内对点迹的帧间共线性进行检验.当n≥M时,计算

②若Pn(ρ,θ)=0,直接滤除相关点迹;反之则由算法1根据Hm(ρ,θ)值恢复得到
③记目标最大可能运动速度为Vmax,扫描周期为Tscan,比较中每个点迹对之间是否满足速度约束条件

满足式(6)的共线点迹称为有效点迹,将它们输出到有效点迹集合Sep中,进行下一步处理.
3.2 目标检测与航迹恢复
在积累检测周期N内,对Sep中所有有效点迹,运用数据匹配Hough 变换算法在参数空间完成目标检测与航迹恢复.
(1)数据匹配Hough变换
本文所述数据匹配Hough 变换算法在标准Hough变换基础上,观测数据原点自适应于筛选后有效点迹.已有研究结果表明,当目标航迹位于观测区域中心时,Hough 变换参数空间分辨能力最优.使用Sep中点迹的几何位置中心作为观测数据新原点,即将式(1)所示标准Hough变换修正为

其中,(x0,y0)为调整后观测数据原点.
取定累加矩阵大小为Nρ×Nθ,参数空间θ维分辨力保持不变,而ρ维分辨力也自适应于有效点迹数据.此外,为避免强目标对微弱目标检测的干扰,采用二进制积累准则;为降低量测误差影响,对变换后积累矩阵进行平滑处理.
(2)过门限目标检测
记平滑后参数单元累积值为A(ρ,θ),采用固定门限γ1进行判决.γ1由需要控制的最终虚警概率Pfa决定,二者之间的解析关系将在第4节中给出.
进一步对过门限参数单元进行凝聚处理,获取同一目标唯一的参数坐标估计值(ρm,θm).
(3)航迹恢复与点迹提取
对所有的(ρm,θm),考虑式(7)所做改进,依据如下直线方程在Sep中恢复目标航迹并提取对应关联点迹

提取航迹m关联点迹时,按时序采用点线距离作为判据,即对sl,n∈Sep,若满足
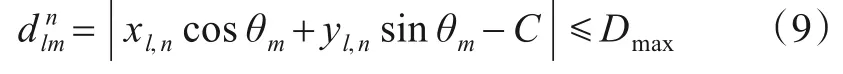
则将点迹sl关联到目标航迹m中,其中Dmax为可允许的最大偏差距离.若n时刻对应航迹m,Sep中所有点迹均不满足式(9),可进一步回溯预检测输出数据集;若存在多个满足条件点迹,则依据最近邻原则选取相关点迹.
最后,依据关联结果对目标检测与航迹恢复结果进行进修正,最终得到确认目标集为

4 性能分析
根据随机游程分布理论[17,18],二元随机序列的游程分为4 种,其中M-游程为可重叠计数游程.1988 年,Ling 等人[19]首次给出N次独立贝努利试验中长度为k的M-游程出现次数的概率分布函数,即为II型k阶二项分布.记Hough变换参数单元取值为mS,为便于应用随机游程分布理论,将mS表述为
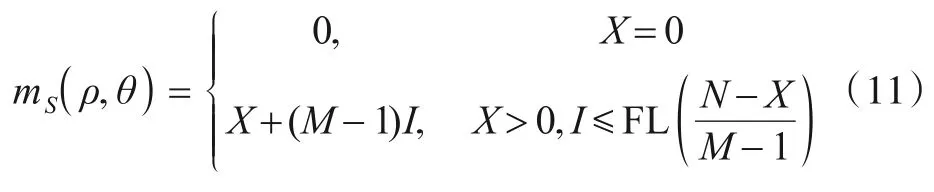
其中,X为随机二元序列{Hn(ρ,θ)}(1 ≤n≤N)中长度为M、重叠度为M-1 的M-游程的出现次数;I为长度不小于M的游程簇个数.
借鉴文献[17]所使用的推导方法,采用本文相关符号标识,可得X和I的联合概率分布为


其中,i的取值除满足式(11)的约束条件外,还应满足
由此可得,不考虑其他疑似航迹影响,参数空间杂波单元和目标单元的取值概率分别为
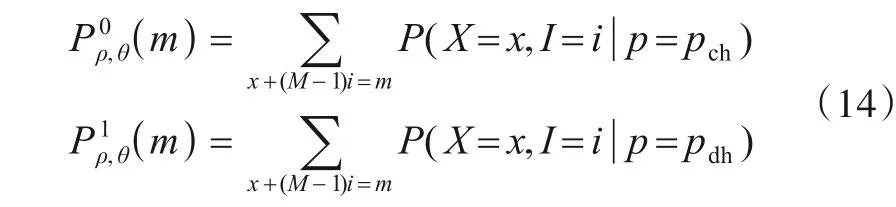
其中,pch和pdh分别为满足速度约束条件单次观测对应参数单元被击中的概率,其计算公式及具体推导过程如下.
不考虑航迹共线或共点,假设目标运动速度服从[0,Vmax]间均匀分布,雷达扫描周期为Tscan,积累周期为N帧,则观测空间平均航迹长度为时刻预检测输出单帧杂波点迹数量服从参数为λ的泊松分布,位置在观测空间内服从均匀分布,则n时刻杂波航迹对应参数空间单元(ρ,θ)被杂波点迹至少击中(即杂波点迹落入杂波航线L0上)l次的概率为

观测空间相邻周期一对杂波点随机落入航线L0,落点服从[0,L0)上均匀分布,则该对杂波点不满足速度约束条件的概率为

假设相邻周期该航线上落入杂波点数分别由随机变量l1和l2表示,l1和l2相互独立且概率分布函数均满足式(15).则单次观测杂波点迹满足速度约束条件且使得Hn(ρ,θ)>0成立的概率为

对真实目标航迹,在n时刻无论是目标点迹还是满足速度约束的杂波点迹,一次也不击中该参数单元的概率为

故参数空间目标单元被击中,即Hn(ρ,θ)>0 成立的概率为
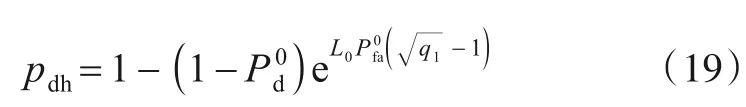
参数空间同时存在的其他疑似航迹及其所属点迹都可能击中待检测单元,从而对待检测单元取值产生影响,表现在观测空间就是疑似航迹间可能出现共点或共线的情况.考虑这种影响,将参数空间杂波与目标单元的取值概率分别修正为

具体推导过程及相关参数定义如下.
在参数空间考察航迹共点(或共线)影响.记目标数量为Nt,参数空间分辨单元总数为Nρ×Nθ,不考虑航迹共点或共线影响时参数空间杂波和目标单元的取值概率分别为P0(x)和P1(x),则从统计平均的角度分析,经点迹筛选后杂波虚假航迹总数为

考虑Hough变换的特点,不难得到参数空间杂波单元和目标单元被其他航迹所属点迹击中的平均概率分别为

其中,Σ1=Nc+Nt-1 为疑似航迹总数,m0和m1分别为疑似航迹存在条件下单个杂波和目标航迹包含点迹数的均值,且有

由此可得,考虑航迹共点(或共线)影响,参数空间杂波单元和目标单元取值概率分别为
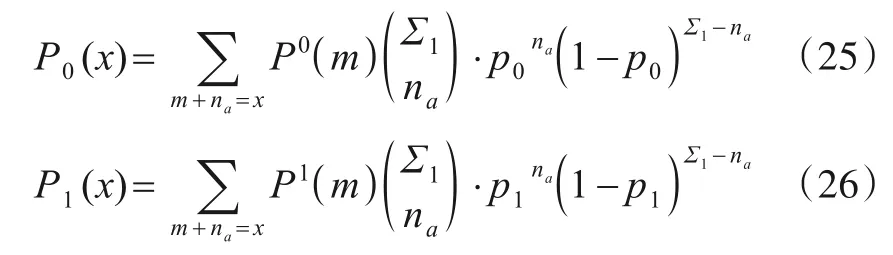
当检测门限为γ1时,对待检测参数单元(ρ,θ),不难得到目标检测的虚警概率为
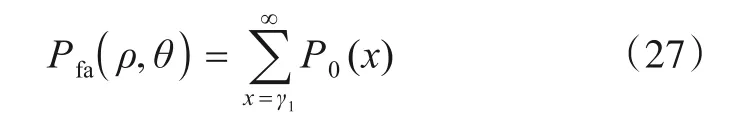
参数空间目标检测不出现虚警要求所有可达单元均不会出现虚警,考虑对目标最不利情况,则最终的虚警概率可计算为

假设目标在积累检测期间保持直线运动且默认目标点迹均满足速度约束条件,则最终的发现概率可表示为
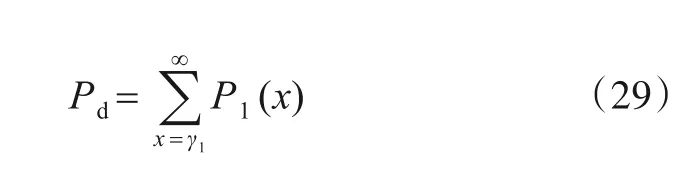
依据上述理论推导结果,图2所示为不同杂波点迹密度λ下本文所提MHT-TBD 检测器虚警概率随检测门限γ1的变化关系,图3 所示为该检测器的检测性能,相关参数取值如下0.85,Nt=5,VmaxTscan=100 m,Nρ=256,Nθ=180.
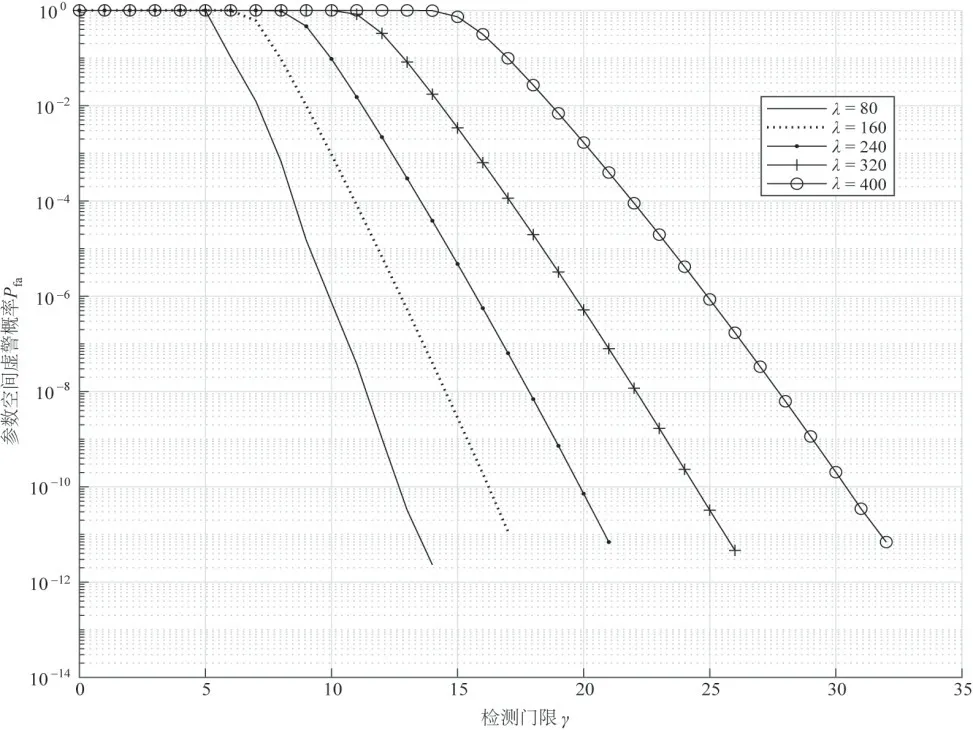
图2 MHT-TBD检测器虚警概率随门限变化关系

图3 MHT-TBD检测器的检测性能(M=3)
图4 所示为其他条件不变,N,λ和M取不同值时MHT-TBD 检测器的检测性能,作为参考同时给出速度约束二进制积累类TBD 最优检测器的检测性能.该最优检测器等价于直接对所有预检测输出点迹进行速度约束筛选后再进行二进制积累检测.
由图4可知,N越大或λ越小,检测性能越接近最优检测器器;当M=3或M=4时,在较长积累时间(如N≥30)或较低杂波点迹密度(如λ≤100)下,主要虚警概率范围(如10-6以上)内MHT-TBD检测器的性能十分接近最优检测器;随着M的增加,检测性能出现一定程度下降,但即使在M=7,M=20 和λ=300 时也可保证最终的发现概率在0.5以上.最优检测器虽具有理论最优检测性能,但平均需要λN次速度筛选运算,计算量随N和λ呈爆炸性增长,密集杂波背景下难以工程实现.通过引入多帧共线约束条件,最坏情况下也可平均将点迹筛选环节运算量降低为原来的

图4 不同N,λ和M条件下MHT-TBD检测器性能比较
5 仿真分析与讨论
5.1 仿真条件
观测区域为6 km×6 km矩形区域,分辨力取为30 m×30 m.雷达扫描周期为5 s,积累检测30个扫描周期.仿真在预检测输出点迹数据集上完成,预检测门限γ0由所要求初始发现概率决定,在给定信杂比、目标起伏特性和杂波幅度分布特性下,初始虚警概率和杂波点迹密度λ也随之确定.仿真目标匀速直线运动,起始位置和运动速度随机设定且雷达观测均方根误差5 m.单帧杂波点数量服从参数为λ的泊松分布,出现位置在整个观测区间内随机均匀分布.
对MHT-TBD 检测器,取滑窗长度M=3,参数空间大小固定为Nρ=256,Nθ=180,末级检测门限γ1依据图2 所示理论结果设定,以保证输出虚警概率Pfa≤10-4,其中取,平滑处理采用3Δρ×3Δθ的二维高斯窗.
5.2 算法有效性实例分析
以同时存在5个目标的某次典型仿真结果为例,说明本文所提方法关键步骤的有效性.仿真目标的信杂比均设为9 dB.按照的要求设置γ0,在目标Swerling-I 型起伏、杂波瑞利分布的假设下,可以预计
图5 所示为整个积累检测周期内预检测输出的点迹,其中“*”表示杂波点迹“,○”表示目标点迹;图6所示为点迹筛选结果“,△”表示筛选后的有效点迹.比较图5、图6可知,本文所提点迹筛选算法可大幅抑制杂波点迹.

图5 积累检测周期内预检测输出点迹集仿真结果

图6 基于共线和速度约束后点迹筛选处理结果
图7所示为DMHT 变换和参数空间平滑后结果,调整后的观测区原点以符号“+”表示(图6).图8 所示为门限检测和凝聚处理结果,其中依据理论分析取检测门限γ1=22,红框所示为凝聚后的目标参数坐标估计位置.由图可知,自适应调整后观测数据原点接近多目标航迹的中心,变换后参数空间目标单元分布较均匀,利于多目标分辨和检测;使用理论预测门限可正确发现所有目标且对本仿真算例在整个参数空间无虚警产生.图9 所示为航迹恢复和点迹提取结果,点迹提取仅在有效点迹集Sep中进行,所提取关联点迹以黑色“+”符号表示.预检测输出的绝大部分目标点迹均能被正确提取,杂波点迹剩余较少且主要发生在航迹交叉处.

图7 自适应Hough变化参数空间积累平滑结果
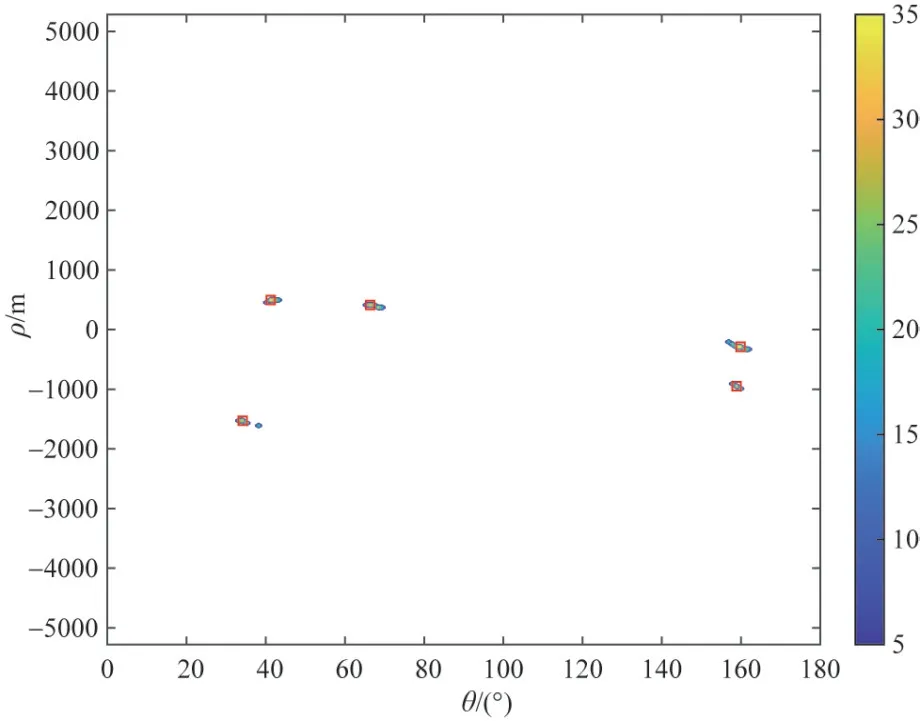
图8 门限检测与凝聚处理后结果

图9 航迹恢复与点迹提取结果
5.3 Monte Carlo仿真结果
为在更多仿真样本和不同λ条件下考察本文方法性能,进行Monte Carlo 仿真试验.取λ分别为80,164,237,316 和398,每种情况独立进行2 000 次仿真试验,每次仿真均设置5 个起始位置和航速航向均随机变化的仿真目标.主要考察4 个指标,具体包括:点迹筛选前后单帧杂波点迹密度变化情况,门限检测时目标航迹正确发现概率,以及航迹恢复和关联点迹提取时的丢点率与错点率.
图10~12 所示分别为针对上述指标的仿真实验统计结果,相关参数设定同上.由图可知,本文所提点迹筛选算法能够大幅剔除杂波虚假点迹,且关于筛选前后λ的变化情况,实验结果与理论预测较一致;在给定虚警概率下,参数空间目标发现概率虽随λ增加呈现一定下降趋势,但总体均保持在92%以上;仅回溯有效点迹数据集,航迹恢复和点迹提取也可保证较低的丢点率和误点率;5 组共计10 000 次仿真实验中,仅在λ=316 时观测到1 次虚警发生,目标检测的虚警概率也与理论分析结果相吻合.

图10 点迹筛选前后单帧观测杂波点迹密度对比
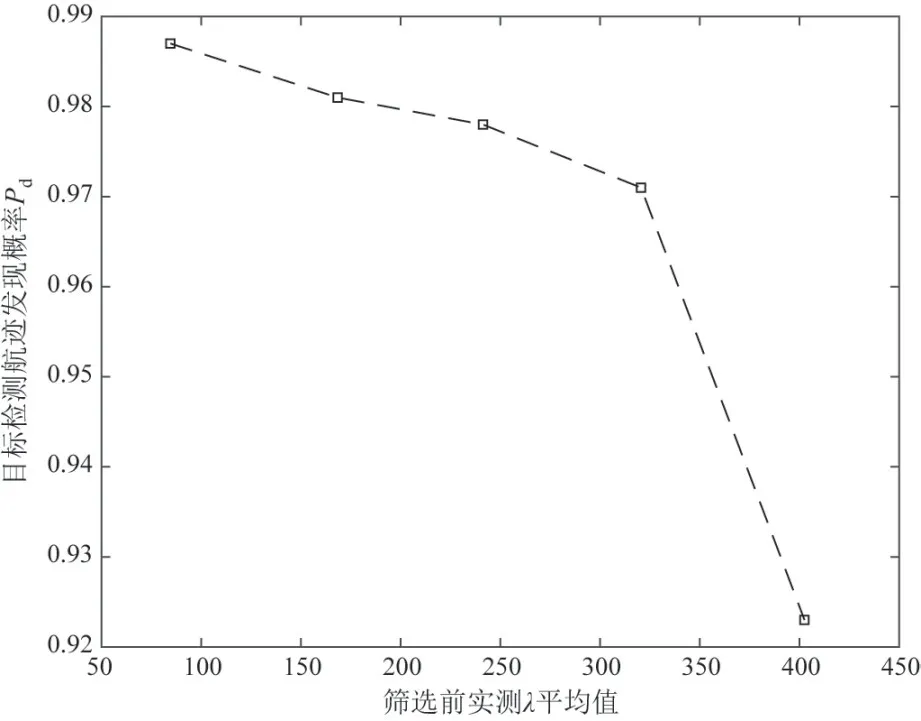
图11 不同杂波点迹密度下目标航迹正确发现概率
6 实测数据分析验证
基于某X 波段导航雷达实测数据进一步对本文方法进行分析与验证.该数据集于2016 年9 月在山东省烟台市芝罘湾采集.试验时,雷达架设于海岸高楼楼顶,架高约88 m;采用脉冲方式工作,距离分辨力12 m,扫描周期2.5 s.因该试验主要针对海杂波特性研究而开展,故无合作目标配合.测试数据总长度64帧,图13所示为最后一帧的P 显结果,选取一个4 km×4 km 且具有较多活动目标的海上区域作为算法验证的输入数据区,具体位置如图13中方框所示.

图12 不同杂波点迹密度下点迹提取性能
图13 实测数据原始回波图像
考虑港内多为慢速目标,首先采用隔扫描周期采样的方法将原始数据降为32帧(等价于扫描周期变为5 s).图14所示为本文方法的处理结果,共检测到疑似目标13 批,其中预检测输出单帧过门限点迹数平均约为78个,依据理论分析结果设置检测门限γ1=10.相同检测门限下,采用速度约束二进制积累最优HT-TBD 检测算法,所得检测结果与本文方法一致,唯过门限参数单元积累值高出本文方法平均约0.46 dB.在所检出疑似目标中,A1,A2和A3经与相关资料进行位置比对,确认为进港引导灯桩,其RCS经定标测量在3 m2左右;T1和T2经点迹时序以及运动状态分析,基本可确认为运动目标;其他已检出目标均为疑似慢动或漂浮目标,因无AIS等信息比对,尚无法最终确认.
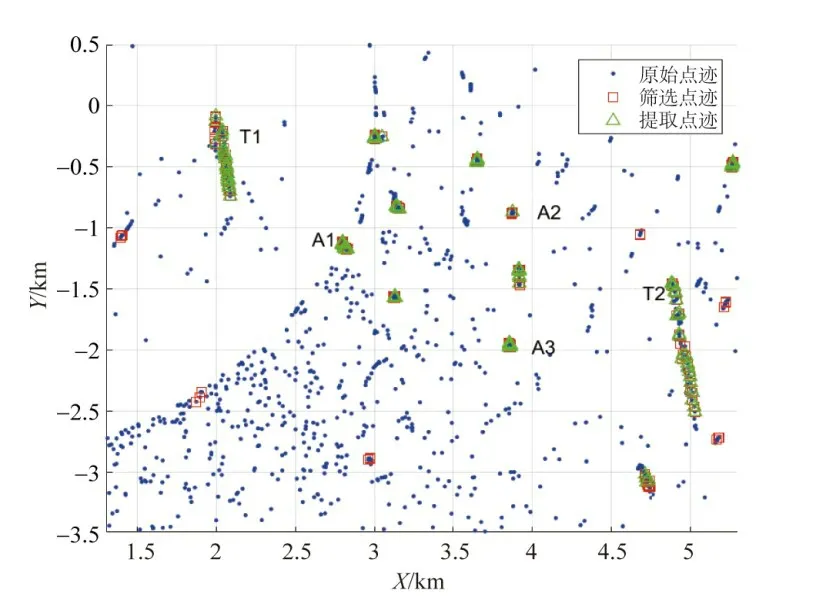
图14 实测数据处理结果
7 结论
本文提出一种基于修正Hough 变换的雷达海面微弱目标TBD检测新方法.针对密集杂波背景,通过基于修正单帧Hough 变换以及引入多帧连续共线和速度约束条件,可大幅降低杂波点迹密度;在此基础上,基于数据匹配批处理Hough 变换在参数空间完成多目标二进制积累检测和原始点航迹提取.所提方法能保持较高目标发现概率和较小计算量,同时可显著提升杂波虚假航迹抑制能力.
Hough 变换类TBD 检测方法的固有缺陷是难以有效应对慢动或机动目标.下一步研究中,将结合其他TBD 检测算法对本文方法进行改进,以提高对慢动或弱机动目标的检测性能.

