非抽取小波边缘学习深度残差网络的单幅图像超分辨率重建

王相海，赵晓阳，王鑫莹，赵克云，宋传鸣

（1.辽宁师范大学地理科学学院，辽宁大连 116029；2.辽宁师范大学计算机科学与信息技术学院，辽宁大连 116081）

1 引言

卷积神经网络（Convolutional Neural Networks，CNN）［1，2］作为一 种具有 深层结 构的前 馈神经网络（Feedforward Neural Networks，FNN），其强劲的表征学习能力被计算机视觉领域所关注［3，4］，其中CNN 所具有的网络权值共享特性以及对平移、缩放的高度不变性被应用于图像的超分辨率重建中，比如最早出现的超分辨率重建CNN 模型SRCNN［5］及其改进模型FSRCNN（Fast SRCNN，FSRCNN）模型［6］，前者采用3层卷积层用以学习LR 图像和相应HR 图像之间端对端的直接映射；后者则通过将SRCNN 预处理中的双三次插值替换为后处理的反卷积.这两种模型为基于CNN 图像超分辨率重建研究奠定了基础.

随着研究的不断深入，如何通过加深CNN 层数来提高重建图像的质量，以及如何减轻模型的计算负担一直受到重视.对于提高CNN 层数的问题，有两个比较经典的模型：VDSR（Very Deep Super-Resolution，VDSR）［7］和DRCN（Deeply-Recursive Convolutional Network，DRCN）［8］，前者设计了20 层的卷积层，后者则通过将同一卷积层进行16次递归提高CNN的层数.进一步为了解决更深层次网络所带来的梯度“爆炸”和参数训练增量问题，VDSR 采用了残差学习与增大学习率的方法，DRCN 模型则采用了递归监督和跳跃连接的方案；对于模型的计算负担问题，文献［9］提出一种子像素CNN 模型ESPCN（Efficient Sub-Pixel Convolutional Neural network，ESPCN），该模型通过把各低分辨率通道的同一位置像素视为高分辨率通道的对应子像素，将低分辨率图像特征按照对应位置周期性的插入到高分辨率图像中，实现图像分辨率的提升；文献［10］提出一种基于拉普拉斯金字塔超分辨率模型LapSRN（Laplacian pyramid Super-Resolution Network，LapSRN），其通过拉普拉斯金字塔框架渐进重建多等级高分辨率残差，并采用Charbonnier 损失函数与跳跃连接实现了模型的有效训练.此外，近年来生成对抗网络模型（Generative Adversarial Network，GAN）也为超分问题的求解提供了新思路.文献［11］提出了SRGAN 网络模型用于图像的超分辨重建，取得了更加逼真的重建图像；文献［12］提出了一种感知生成对抗网络（Super Resolution Perceptual Generative Adversarial Network，SRPGAN），用实例标准化取代原始SRGAN 模型中的批量标准化，进一步提升了重建图像的质量；文献［13］针对SRGAN 模型重建图像的伪影问题，提出了一种增强SRGAN 模型（Enhanced SRGAN，ESRGAN），利用稠 密残差 块（Residual-in-Residual Dense Block，RRDB）作为基本单元，借用相对GAN 网络［14］思想，通过预测两幅图像的相对真实性对感知损失做出改进，在有效去除伪影的同时进一步提升了图像的超分重建质量.

尽管目前基于深度神经网络的图像超分辨率重建得到了较好的发展，但仍有许多工作尚需研究和完善，比如网络的结构有待创新、效率有待提高，对有效特征的挖掘还有待加强，重建超分辨率图像的质量还被期望进一步提升等等.近年来基于多尺度几何分析（Multiscale Geometrical Analysis，MGA）的图像稀疏表示取得了很好的发展［15，16］，文献［17］构建了一种Wavelet域深度残差学习算法用于图像去噪和超分辨率重建；文献［18］构建了一个基于图像Wavelet变换子带的深度学习网络，将输入的低分辨率图像作为图像Wavelet变换的低频子带，通过预测图像Wavelet变换的高频子带系数作为构建高分辨率子带“丢失”的细节来实现超分辨率图像的重建.

上述两种方案对图像Wavelet 变换后的各子带采用了相同的学习策略.事实上低频与高频子带表现出不同的统计特性，低频子带通常会显著影响着两幅图像的主体内容相似程度；而高频子带则在图像边缘等梯度值较大的区域发挥着重要作用.受此启发，本文首先对LR 图像与HR 图像非抽取Wavele（tNon-Decimated Wavelet Transform，NDWT）的低频和高频子带的统计特性进行分析，进而提出一种基于NDWT 边缘学习的深度残差网络模型NDW-EDRN 用于单幅图像超分辨率重建，对输入图像NDWT 低频和高频子带采取不同的学习策略来学习LR 子带与HR 子带间的映射关系，对低频子带采用基于稠密跳跃连接的“整体式”学习方式，而对高频子带则采用了一种基于块U-net 级联的“缺失式”学习方式，即放弃原始将低、高分辨率图像的高频子带直接进行学习，利用网络模型学习它们间更为稀疏的差值，使网络学习更具针对性.

2 单幅图像超分重建及图像NDWT 子带分析

2.1 单幅图像超分辨率重建

单幅图像超分辨率重建是指从观察到的包含模糊、下采样以及噪声等退化情况的单幅低分辨率图像中估计出高分辨率图像的过程［19］，其成像模型的一般过程可描述为

其中，ILR是观测到的低分辨率图像，B是模糊矩阵，IHR是原始高分辨率图像，(m，n)是水平与竖直方向的降采样因子，实际应用中一般假设二者相同，Nσ是方差为σ的噪声.

单幅图像超分辨率重建一般可以看成是图像经由IHR退化为ILR的反问题，参见图1.由于图像IHR在退化过程中损失了不可逆的高频细节信息，因此该反问题的解并不唯一，从而导致图像超分辨率重建问题具有高度的不适定性.

2.2 非抽取Wavelet变换

作为标准离散Wavelet 变换的扩展，文献［20～22］等基于不同的应用领域提出了非抽取Wavelet 变换NDWT.假设低通滤波器H、高通滤波器G为正交镜滤波器（Quadrature Mirror Filters，QMF）［23］，即对于由有限个非零值序列｛hn｝定义的H，满足如下正交性：

对于信号{…，x-2，x-1，x0，x1，，x2，…}，H 滤波、G滤波过程为

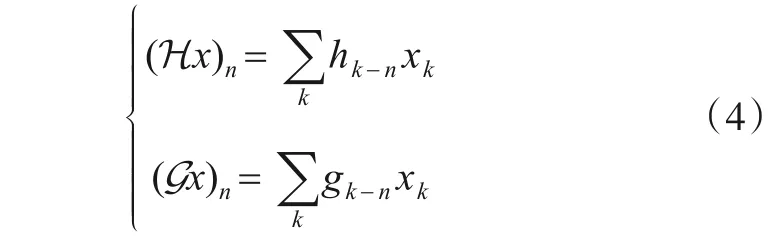
进一步定义D0和D1分别为基于偶数和奇数的二抽样算子：

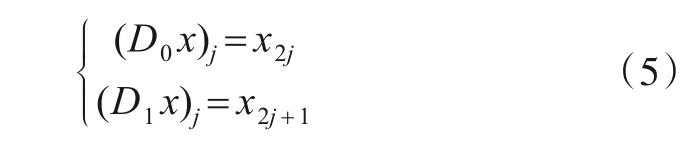
标准离散Wavelet 变换是基于H、G和D0实现的［21］：对于原信号c：｛cm|m=0，1，…，n-1｝，假设其具有周期性的边界条件，定义第J层的平滑逼近信息cJ为

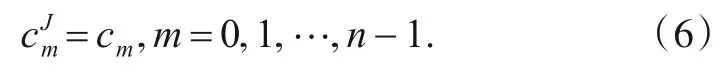
对于j=J-1，J-2，…，1，0，递归的定义信号第j层的平滑逼近信息cj和细节信息dj：

其中cj和dj的长度分别为2j.可以看出在式（7）的递归分解中，仅有当前层的平滑逼近信号参与下一层的平滑逼近信息与细节信息的分解.

NDWT对上述标准Wavelet过程进行了扩展，通过D1和D0算子在各个尺度上提取奇、偶索引的平滑逼近信息和细节信息：对于初始信号cJ，通过D1GcJ和D0GcJ获得奇、偶索引的细节信息，通过D1HcJ和D0HcJ获得奇、偶索引的平滑逼近信息，每一个奇、偶信息的长度分别为n/2，这样所获得的细节信息（即小波系数）的总长度为2×n/2=n.

进一步对所获得的奇、偶索引的细节信息分别进行D1G和D0G操作，获得当前层的细节信息；对所获得的奇、偶索引的平滑逼近信息进行D1H 和D0H 操作，获得当前层的平滑逼近信息，这样始终能够保持每层分解所获得的细节信息的总长度为n.该过程重复进行，直到完成整个变换.具体过程参见图2，其中d0和d1为第一层的细节系数，长度分别为n/2；d00、d10、d01和d11为第二层的细节系数，长度分别为n/4.

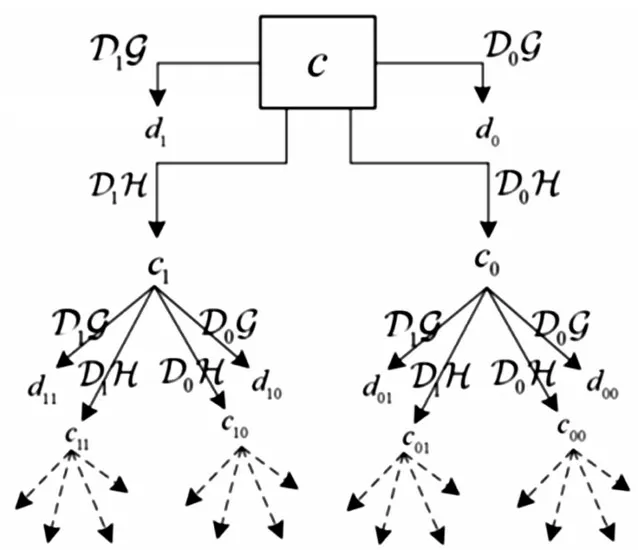
图2 NDWT过程流程图[22]

NDWT不仅保留了离散Wavelet变换的多尺度特性和方向特性，同时还具有平移不变特性，更多的获得了信号的细节信息，从而为图像融合、图像超分辨率重建等应用奠定了基础.

2.3 图像NDWT子带特性分析

选取文献［24］提供的Set5 中具有丰富细节的bird图像和边缘明显的butterfly图像作为测试对象.

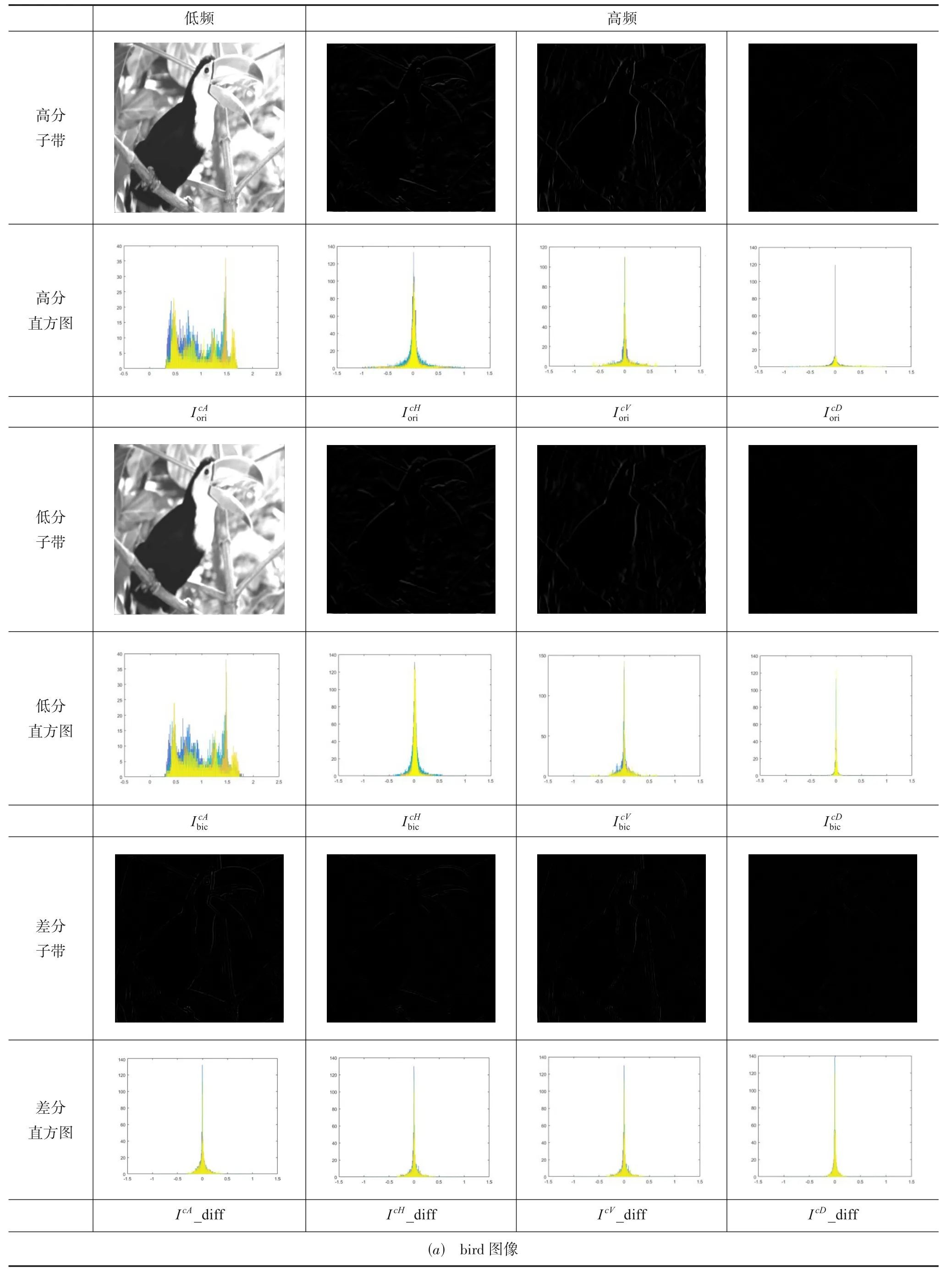
图3 图像NDWT子带、差分子带及其直方图统计

对图3的各子带及其统计结果进行观察与分析后，可分别得到以下结论：

（2）不论是IcH还是IcV，IcD，其统计直方图均显示图像的任一高频子带绝大多数系数值分布在零点附近，只有少量系数值较大，具有“高峰拖尾”的稀疏性；

（3）从高频差分子带可看出同一方向高频子带差值较大的系数大多位于图像退化过程中所丢失的边缘、拐点等梯度值较大的位置.

基于以上对各子带特性的分析与相关文献的支撑［25］可知：低频子带的恢复决定着图像的主体内容质量，它对应着较高的峰值信噪比值；高频子带的恢复则显著影响着图像的视觉感知质量，它呈现出较高的结构相似度.因此，本文设计两种不同的学习策略与网络结构来更有针对性地对图像的低、高频子带进行区分学习.对于低频子带，采用稠密跳跃连接的“整体式”学习方式，将低分辨率图像的低频子带作为网络的输入，将高分辨率图像的低频子带作为网络的输出，网络采用稠密跳跃的连接方式，使深层次的网络学习更加充分，避免梯度弥散现象；对于高频子带，则采用块U-net级联的“缺失式”学习方式，将低分辨率的高频子带作为网络的输入，将高、低分辨率图像的高频子带的差值作为网络的输出，网络采用编解码与块级级联的方式，增强稀疏性的同时，防止梯度弥散，使低分辨率图像所丢失的边缘等高频信息得到有效的补充.

3 NDWT边缘学习的深度残差网络

由前面的分析可以看出，图像经双三次插值后的LR 图像与原始HR 图像之间相比，主要在于图像退化过程中高频信息的丢失，而低频信息较为相近.为此本文构建如图4 所示的深度残差网络模型NDW-EDRN（Non-Decimated Wavelet Edge learning using Deep Residual Networks，NDW-EDRN）用于单幅图像超分辨率重建.

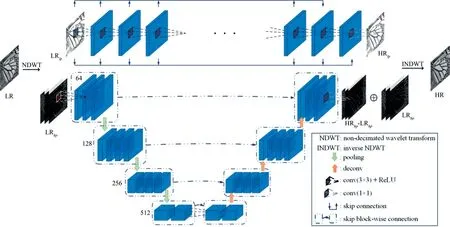
图4 深度残差网络模型NDW-EDRN结构图

模型NDW-EDRN对图像的NDWT子带采用了不同的学习方式，其中对低频子带间的映射关系学习采用了“整体式”的网络结构［17，18］，网络采用了20 层的卷积操作，并通过稠密［26，27］的跳跃链接结构来充分学习低频子带内所包含的信息；而对高频子带间所丢失的边缘信息则采用“缺失式”的网络结构进行学习，表现为利用文献［28］所提出的U-net 架构与文献［29，30］所提出的深度残差学习策略，构建一个学习丢失边缘的端到端网络，提取出图像中更加深层且复杂的特征，弥补在图像退化过程中所丢失的重要信息.主要包含以下四种操作：

（1）Conv(3×3) +ReLU：每阶段获取特征图的主要方式；

（2）Conv(1×1)：位于网络的最后一层，用于映射期望；

（3）Pooling与Deconv：扩大感受野并还原；

（4）Skip block-wise connection：本文在传统U-net通过级联对应阶段子特征图增强网络强度的基础上，把单子特征图拓展为块子特征图，以像素级累加的方式将网络的编码、解码两端更紧密地联系在一起，进一步提升网络的有效性.

对于模型上线路的稠密链接部分旨在让当前第l层的输入接收来自前［l-1，l-2，…，0］各层的输出.若定义第l层的输入为Il，输出为Ol，那么

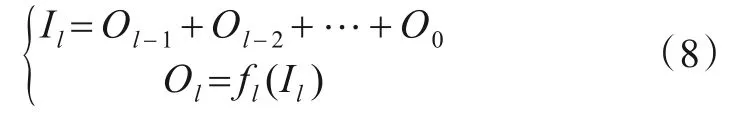
此处的fl是对应当前l层的运算处理.

对于模型下线路的改进U-net 部分旨在采用如下图5所示的以块为单位的跳跃级联，达到信息紧密传递的目的.

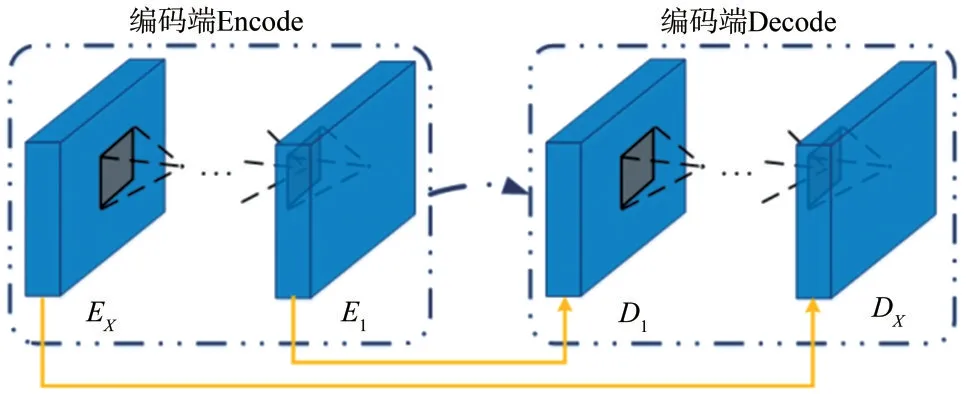
图5 块级级联示意图

模型的物理含义是对低频分量而言，衡量LR 与HR 间对应子块的相似程度；对高频分量而言，训练出一组能够有效描述LR 对比HR 所缺失的边缘算子，来有效补充高频信息.

4 实验与分析

4.1 实验设置

训练集：BSD500［31］（去除与测试集重复的部分）、General00［6］和91images［32］；测试集：Set5［24］、Set14［33］和Urban100［34］；采用双三次函数模拟下采样因子为2和4的Y通道退化；设置“整体式”网络中子带块大小为64×64“，缺失式”网络中子带块大小为192×192；网络模型采用Adam优化算法求解［35］，设置初始学习率为0.001，在第40个周期后衰减为0.0001.实验环境为Inte（lR）Xeon（R）CPU E5-2630 v4@2.20 GHz在Ubuntu 14.04，Caffe7.5平台上进行，NVIDIA Titan X GPU用于网络训练.

4.2 定量与定性分析

表1给出与SRCNN［5］、VDSR［7］、SRMD［36］和DSRN［37］非多尺度且网络层数小于等于20的深度学习模型，以及与DWSR［18］和WaveResNet［17］多尺度深度学习类模型分别放大2 倍与放大4 倍的PSNR 与SSIM 对比实验结果；表2 给出与SRGAN［11］、SRPGAN［12］生成对抗网络模型，以及与DRRN［38］、LapSRN［10］和MemNet［39］非多尺度且网络层数大于50的深度学习模型别放大2倍与放大4倍的PSNR与SSIM对比实验结果.两个表中分别对最优结果做出“加粗”处理，对次优结果做出“下划线”处理.同时图6，7，8，9给出了Set5、Set14与Urban100数据集中的部分重建彩色结果图及其细节处的放大对比图，对各指标的最优及次优结果做出与表1、2中同样的处理.

图6 对比其他非多尺度网络模型放大2倍的细节图

表1 的实验结果显示，所提出的NDW-EDRN 模型较近几年层数小于等于20的主流非多尺度深度学习模型和多尺度深度学习模型在客观评价指标PSNR 与SSIM 表现上均呈现着一定的优越性，除了对Set14放大2 倍的实验结果取得了次优结果，其余均为最优结果.对表1的统计结果进行分析后，可以看出：PSNR的次优结果大多分布于非多尺度深度学习模型实验结果中，而SSIM的次优结果则绝大多数分布于多尺度深度学习模型实验结果中.这说明，非多尺度深度学习模型在恢复图像主体内容，即与原始图像的像素级相似度呈现上表现良好；而基于多尺度的深度学习模型则在恢复图像边缘结构时发挥着重要作用，能获得比非多尺度深度学习模型更为优异的纹理结构级相似度.

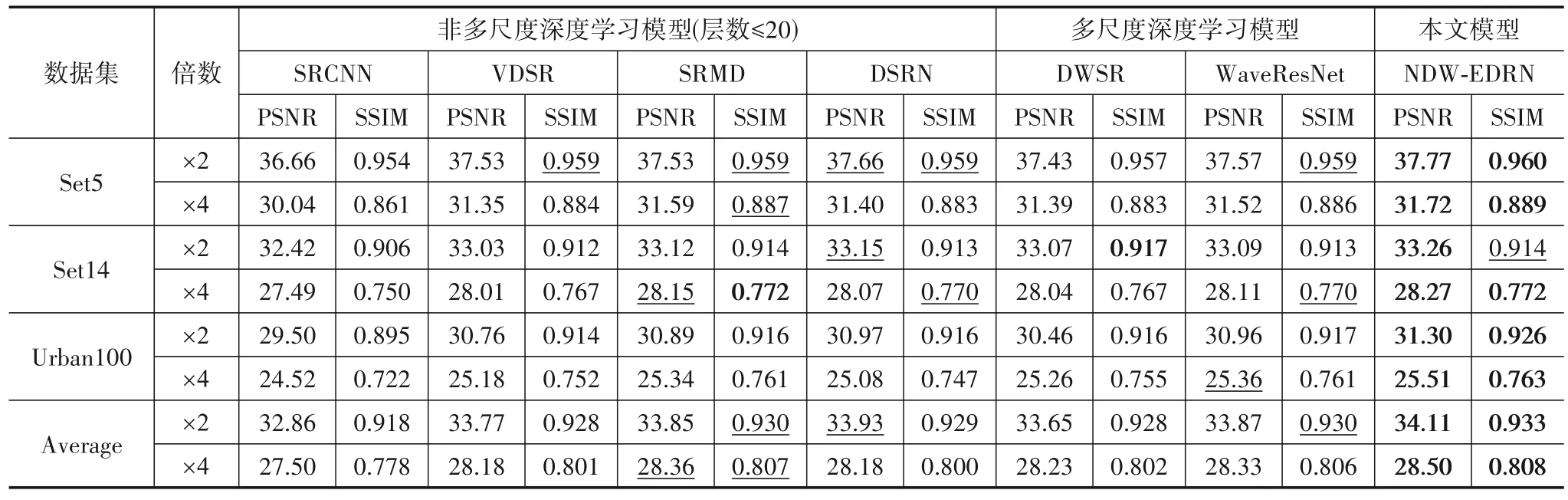
表1 重建图像的定量比较1

表2 展现了本文模型与近几年主流的生成对抗网络模型及层数大于50的主流非多尺度深度学习模型间的实验数据对比，亦可看出，本文模型相较于SRGAN与SRPGAN 在两个评价指标上都表现得更为稳健，更加具备实用性与稳定性；与层数大于50 的主流非多尺度深度学习模型相比，本文模型在部分实验结果中可与之持平甚至超过.

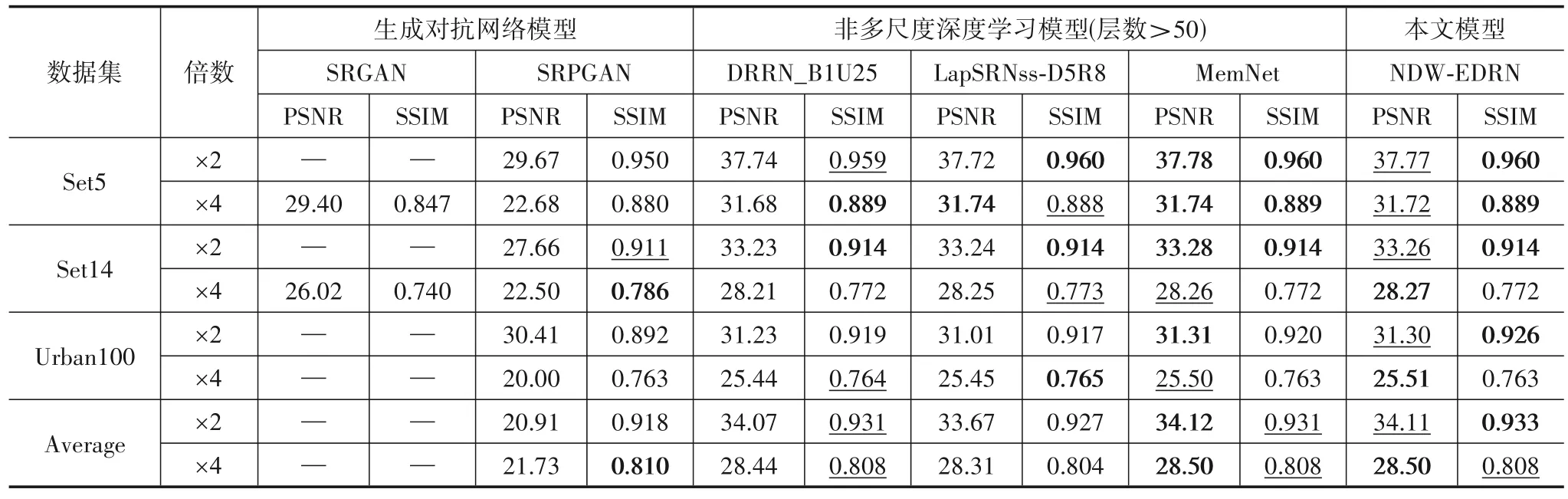
表2 重建图像的定量比较2

图6、7的生成结果同时在主观上也能够看出本文模型在图像边缘细节的重建方面，尤其重建倍数较大时，较其他模型有着明显的优势，比如无论是butterfly图像中蝴蝶翅膀的纹路、lenna图像中的帽檐，亦或是img_087图像中的楼房边缘等都较其他模型重建后的图像边缘更清晰、稳定和有效，在重建质量上表现出一定的优势.

图8、9 所示的多尺度网络模型的重建图像细节对比图显示了在恢复图像纹理、边缘时，这类的网络模型具备一定的优越性与普适性.说明在构建超分辨率重建网络时考虑多尺度变换，利用其提取图像结构信息的这一优势，使网络学习到更加具有针对性的边缘的这一想法是成立且有效的.而本文在此基础上进一步归纳总结非抽取小波变换的低、高频两种子带系数分别呈现的规律后，提出了相应的网络学习模式，使低频子带中所蕴涵的信息被学习得更加完备，使高频子带中所缺失的信息得到指向性补充.

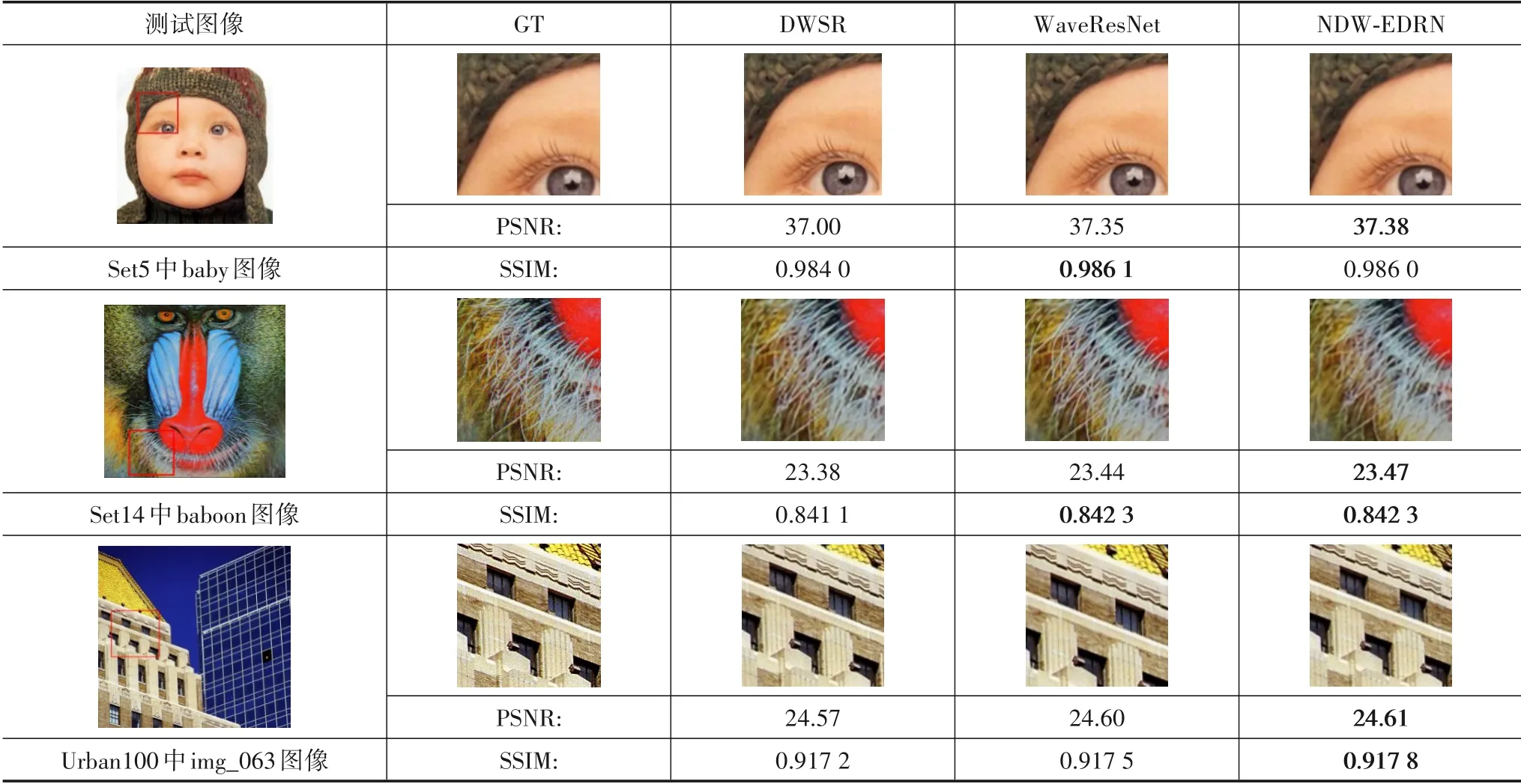
图8 对比其他多尺度网络模型放大2倍的细节图

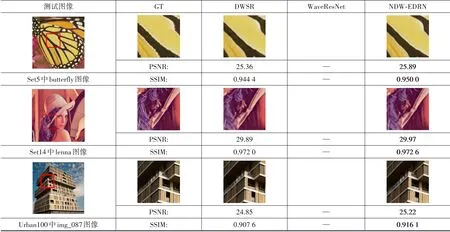
图9 对比其他多尺度网络模型放大4倍的细节(注：WaveResNet网络未公开四倍的预训练模型)

表3 显示了本文模型与其他流行超分辨率重建模型的参数与计算量对比.由于所提模型采用了“整体式”与“缺失式”两种联合学习模式来分别处理低频子带与高频子带，这无疑增加了一定的参数量，这也是需要在未来进一步优化的地方.

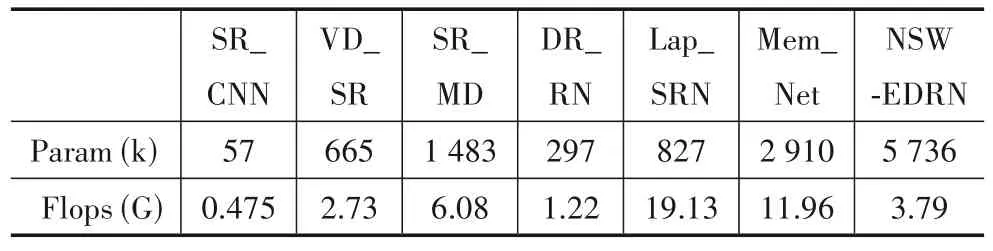
表3 参数与计算量比较

4.3 消融实验

为更全面地评估本模型，表4给出了在非抽取小波变换域下，各子带只采用同一种学习模式网络的消融实验重建结果的定量比较，所有的对比使用与上文相同的超参数设置.

表4 消融实验重建数据集的定量比较

与此同时，由于缺失式网络层数大于整体式网络层数，为避免层数这一嫌疑，将缺失式网络设置为与整体式网络相同的层数.即去除了解码端最后一级子块的最后一层以及该级的块级级联操作，只保留对输入的残差设计，将该网络记为“缺失式_s”网络，那么，采用该“缺失式_s”网络的NDW-EDRN，则记为“NDWEDRN_s”.图10 显式了2 倍消融实验结果图，表5 给出相应的定量评价指标数值，同样采用PSNR 与SSIM 来评估重建图像的质量.

表5 消融实验重建图像的定量比较

由表4、5 与图10 可以看到：双学习模式的网络比任意单一学习模式的网络在提升图像质量与图像结构相似度方面均有些许提升，说明图像中低频信息在得到保证的同时，还被有效地补充进了高频信息.此外还注意到：（1）相较于整体式学习，缺失式学习在网络中更据主导地位，说明重建边缘纹理信息是超分辨率任务中的重点与难点任务；（2）baby 图像的整体式比缺失式网络重建结果好，这可能是因为baby 图像中存在大量平滑信息，整体式网络更完全地保留了原始低分辨率图像中的有效信息，而高频信息较少，导致缺失式网络所需补充的信息少.因此，双学习模式的网络可以融合上述两种网络的优点，既可以对平滑图像学习全面的低频信息，又可以对复杂图像有效地补充高频信息，使网络的学习更健壮、鲁棒.

图10 消融实验放大2 倍的细节(左上角:GT,右上角“:整体式”学习,左下角“:缺失式_s”学习,右下角:NDW-EDRN_s)

5 结论

本文从弥补低分辨率图像高频信息的角度为着眼点，针对传统深度卷积神经网络学习图像细节区域的不足，通过对NDWT 子带间的对比与分析，获得高频子带内系数存在稀疏性、退化图像的低频子带与原始图像的低频子带间存在相似性、图像退化过程中大多丢失高频信息的结论，在此基础上提出一种对低、高频子带采用不同学习策略的深度残差网络模型—NDWEDRN，以解决超分辨率重建过程中难以有效补充边缘细节这一难点问题.该网络可主要分为两部分：一是采用稠密跳跃连接的方式整体性学习低频子带间的映射关系；二是对于高频子带采用一种新型的U-net 模型，主要表现为将图像退化过程中所丢失的边缘作为网络的期望输出，并改进传统U-net 的级联结构，通过采用基于块的跳跃连接来使网络更加有效地学习缺失性边缘.通过大量的实验可以看出，本文提出的NDWEDRN 模型与当前一些经典的单幅图像超分辨率重建网络模型相比，不论主观还是客观都更加有效地提高了重建图像的质量，特别在恢复低分辨率图像所缺失的边缘信息上得到良好效果.