核心素养视域下关于解题教学的思考

西华师范大学 廖 鹰 孙 海

1 研究现状

20世纪80年代，国外对于问题解决的相关研究便已经开始展开，英美《行动的议程》和《cockcroft报告》均将数学教育的核心定义为问题解决，对于问题解决的研究从未停歇，直到如今其仍是教育界研究的热点问题[1].因学生是解决问题的主体，故问题解决的重点便是培养学生的问题解决能力，也即培养学生的数学解题能力.数学解题能力的重要性主要可以从以下几个方面进行分析.从学生本身来看，其是学生自身继续更深入学习必需具备的；从数学学科本身来看，其是理解数学公式定理，构建数学知识体系的基础；从社会角度看，其是选拔性考试所考察的重要能力之一.

但就核心素养角度来看当前中学生数学解题能力，情况并不乐观.就运算能力一项而言，经过对近几年高考题型分析研究发现，其中近六成的题目均会考查学生的运算能力，而根据学生卷面得分情况分析来看，运算错误是失分较严重的地方，这一方面体现了学生自身数学运算能力不足，另一方面也体现了中学数学解题教学仍有改善提高的地方[2].现如今，中高考均颁布新方案，中考1比1录取，禁止中考复读和新高考选科模式，这些重大变化将再一次对中学数学教学给出新的挑战和要求.数学解题教学是中学数学教学的重要组成部分，做好数学解题教学是提高数学课堂质量和培养学生数学核心素养的重要手段，所以我们必须重视中学数学解题教学.数学核心素养视域下的中学数学解题教学研究将从数学本质出发，清晰明确地找到教学中存在的问题，促进数学核心素养与解题教学的有机结合，在提高学生解题能力的同时促进学生的全面发展.

面对种种挑战和变化，不论是从数学教学角度，学生发展的角度和社会角度都说明核心素养下的数学解题教学研究都是势在必行的.

2 研究意义

从数学角度来看，问题是数学的心脏，所以解题教学应是数学教育的核心.数学解题研究即是分析解题所需要的思想观点、策略程序和方法技巧等，以及分析解题过程中的思维活动.通过对解题过程的分析去研究如何解题，教会学生如何解题的同时提高学生数学解题能力[3].

从学生角度看，好的数学解题教学有助于培养学生的数学核心素养，而核心素养的提高也有利于提高学生解题能力，从而更好地实现学生的全面发展.基于长远发展，解题能力的培养也能为我国人才培养奠定基础，在解题教学过程中建构学生数学知识体系，为学生继续接受高等教育做好铺垫.

从社会角度看，中高考改革等现实问题也促进着中学数学教育的发展.中考1比1录取，这种“强制分流”的改变将会给初中学生和家长们带来巨大的压力，同时这种压力也会传递给中学数学教师，将会对教学质量要求更高.同样地，新高考将会要求中学教育变得更加多样化和专业化.因此，中学数学解题教学对中高考这种选拔性考试的重要性不言而喻，核心素养视域下的中学数学解题教学研究对于学生的现阶段和长远发展都有着不可替代的现实意义.

3 核心素养视域下关于解题教学的建议

3.1 一题多变

选好题是学生做好题的前提，教师要激发学生学习数学的兴趣，提高教学质量，首先要做的便是精选题[4].为了实现数学核心素养在课堂上的有效培养，教师在选题的时候要结合学生自身的情况，做好贴合学生实际情况的同时促进学生思维发展，教师自身同时也要吃透题目，做到一题多解和一题多变，这样才能更好地促使学生思维发散.下面是两个一题多变和一题多解的典型模型.

例1(函数模型)

已知抛物线y=x2+bx+c与x轴交于A，B两点，与y轴交于点C，顶点为D.如图1，已知OA=OC=3，求解：

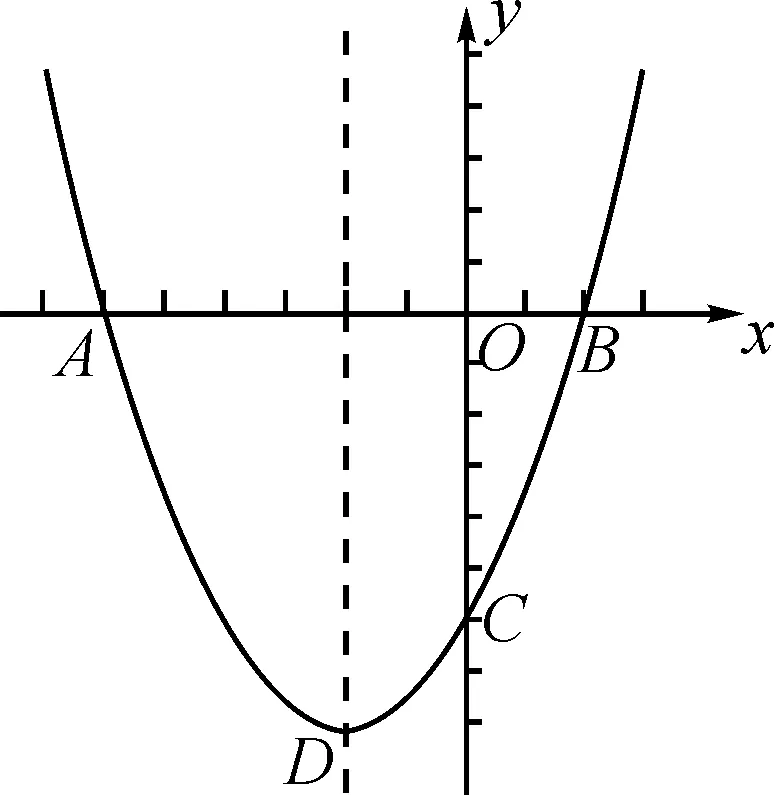
图1

(1)求此函数的解析式.

(2)判断△ACD的形状，并说明理由.

(3)求四边形ABCD的面积.

(4)点P是对称轴上一动点，求使△BCP面积最小的点P坐标.

(5)能否在AC下方的抛物线上找到一点N使△CAN(四边形ABCN)面积最大？最大面积是多少？

(6)能否在y轴上找到一点E，使△ADE为直角三角形(等腰三角形)？若存在，求出点E的坐标；若不存在，说明理由.

(7)在抛物线上是否存在一点E,使S△ABE=S△ABC(S△BCE=S△ABC，S△AOE=S△COE)？若存在，求出点N的坐标；若不存在，说明理由.

对于上述例题，通过变式，教师对初中函数相关知识进行了复习，也考查了其他知识，比如点到直线的距离、勾股定理和“将军饮马”等知识.其中第(1)题考查的便是求解函数解析式，由已知条件很容易求出.第(2)题有多种方法求解，比如利用点到直线的距离求出AD,DC,AC三边然后利用勾股定理判断，也可以求出直线AC,DC的一次方程利用斜率判断.第(3)题可以将图形分割之后再求面积，分割的方法也有多种.第(4)题便涉及到了“将军饮马”问题，利用两点间直线最短求解.第(5)题则需要求出AC下方抛物线上点到直线AC距离最远的点，这需要进行转化，我们发现当将抛物线与直线解析式作差，使其y值最大的点便是我们要求的点.其中第(6)、(7)题考查的是对称性和抛物线的相关知识.

在某些有经验的老教师眼中，这一道题可以给出20多个变式，涉及中学阶段多个知识点，由一点发散或者多点融合.从数学核心素养角度看一题多变，教师通过变式教学可以使学生思维发散，知识点贯通，建构完善的数学知识体系，有利于学生直观想象和数学运算能力的发展.

3.2 一题多解

例2(一线三直角模型)

如图2所示，已知四边形ABCD为正方形，E点为BC中点，CF为∠DCH的角平分线，AE⊥EF，求证：AE=EF.

图2

证明：法一.取AB中点G，证明△AGE≌△ECF，进而得到AE=EF.

法二：设正方形中心为O，证明△AOE≌△ECF，进而得到AE=EF.

法三：过F点作FH⊥BC，先证△ABE∽△EHF，再利用AB∶BE=2∶1和△FCH是等腰直角三角形推出FH=BE，证明△ABE≌△EHF，进而得到AE=EF.

法四：建立直角坐标系求出AE和EF长度；

法五：过C点作直线EF平行线，延长AB交平行线于I，证明△ABE≌△CBI，再证明四边形EICF为平行四边形，进而得到AE=EF.

法六：延长直线CF，AB交于点J，证明△AJE和△EJF为等腰三角形，进而得到AE=EF.

法七：作线段EF关于直线BC的对称图形EF′，证明A，C，F′，三点共线，再证△AEF′为等腰三角形，进而得到AE=EF.

法八：利用A，E，C，F四点共圆，证明∠ACE=∠AFE=45°，△AEF为等腰直角三角形.

对于上述问题，当E点是BC上任意一点时也成立.一题多解，要求的是通过解题，不仅要让学生知道如何求解，而且要让学生思维发散，从不同的角度考虑问题.从数学核心素养角度看一题多解，就本题而言，由一数学模型发散，提出问题，从不同的角度分析和解决问题，在进行逻辑推理，构建抽象结构的同时，锻炼了学生的逻辑推理、数学建模和直观想象能力.

4 结语

本文中是从数学核心素养的角度出发的关于中学数学解题研究的的分析思考，发现了中学教师在教学过程中存在教学方式单一等问题，主要从教师教学方面提出了建议，但由于笔者自身的不足，文章许多方面存在缺陷，认知片面.核心素养的培养非一朝一夕，在今后的研究当中，笔者将会结合实际，更新方法，为中学教育事业献出自己的绵薄之力.