Petri网系统活性保持的充分与必要条件

蔡晓霞，郭承军，陈鹤峰

（广东工业大学 数学与统计学院，广东 广州 510520）

1 引言

活性作为Petri网的重要特性之一，活性问题的研究一直是Petri网理论的重要课题.

目前，已有许多文献研究了状态机（State Machine），标识图（Marked Graph），自由选择网（Free Choice）等Petri网特殊子类的活性问题[1-6].对于普通网（弧上的权重皆为1），文献[7]给出了其保持活性的充分与必要条件.然而对通用Petri网系统的研究是较少的.Barkaoui利用结构分析方法，通过定义受控Siphon，分别给出了Petri网系统活性的必要条件与充分条件[8].文献[9]借助于可覆盖图得到了无关联-ω数网系统的活性判定方法.

本文对Petri网系统活性的充分条件与必要条件进行研究.提出了非前阻塞Siphon的概念，得到了Petri网活性的一个必要条件.在讨论通用Petri网的活性的判定问题时，借助于Petri网系统的状态方程和线性方程组理论，对弱活性加以“齐次线性方程组仅有正整数解”这一限制，得到了Petri网活性的充分条件，并通过构造增广Petri网得到了一种新的活性判定方法，对丰富和发展Petri理论有一定的意义.

本文的安排如下：第2、3节给出了一些相关的Petri网基本概念及结论，并定义了Siphon非前阻塞的概念.第4节给出了Petri网活性的必要条件.在第5节中，以一类简单网为例，利用线性规划方法判定Siphon是非前阻塞的，降低了计算复杂度.第6节借助Petri网的结构特征及线性方程组的理论知识，找到了判别Petri网活性的充分条件，并在下一节中，通过构造增广Petri网得到了活性判定的方法.最后，第8节总结了本文的工作，并对后续可研究内容进行展望.

2 Petri网的基本概念

本节中，简要阐述需要用到的有关Petri网理论定义，常用的记号以及基本结论. 详细内容可参考文献[10].

（1）P与T分别称为库所集合与变迁集合，而且|P|=m<∞，|T|=n<∞，P≠∅，T≠∅，P∩T=∅.|*|为集合*的基数.

（2）F⊆(P×T)∪(T×P)是有向弧的集合.

（3）W:F→N+为映射，它给所有的有向弧分配权重值.其中，①整数集合记为Z，非负整数集记为N，正整数集记为N+=N{0}.不超过k的非负整数记为Nk={0,1,2…,k}，不超过k的正整数记为=Nk{0}..

3 Petri网的相关结论

4 Petri网活性必要条件

当Petri网是活的时候，它具有某些特定的行为特性，这些行为特征就是Petri网保持活性的必要条件.如果存在某算法，它能验证上述某些必要条件不成立，并且该算法的复杂度是网规模的多项式函数，那么，该算法能有效地判定Petri网是非活的.

5 非前阻塞的判定

定理5.2 如果线性规划(2)的最优值w*<0，则定理5.1中的SiphonS是非前阻塞的.

注:由上述推理过程，定理显然成立，详细过程略去.

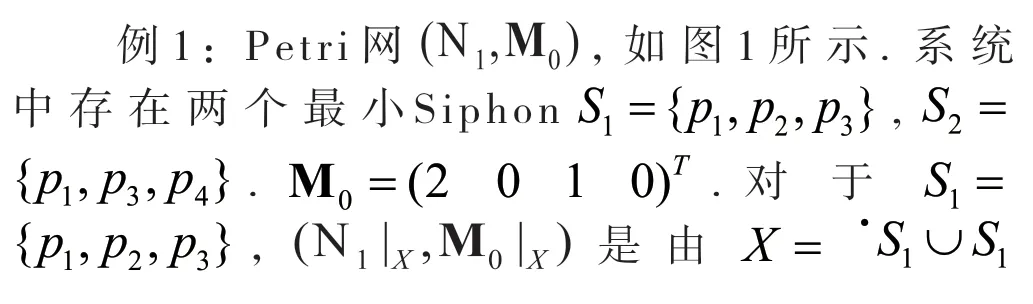
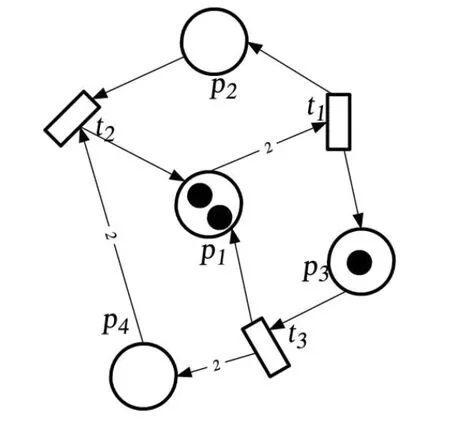
图1 例1的Petri网系统

图2 例1中由x生成的子系统

代入线性规划（2）求解，可得其最优值*w=−∞，为无界解.由此，定理5.2的条件成立，从而SiphonS1是非前阻塞的.同样的方法，可以判定S2也是非前阻塞的.

对于有汇合的Petri网的无阻塞的判定，限于篇幅关系，本文不再详细阐述，是后续研究内容.

6 Petri网活性充分条件

Petri网能否保持活性，是Petri网理论研究及其应用系统建模聚焦的核心问题.对于规模（网节点数，有向弧的条数，token数目）较大的网，由于系统演化过程中，状态呈爆炸式的增长，采用可达图分析的方法，需存贮可达状态及状态转化过程，计算复杂度过高.本节借助Petri网结构特征及线性方程组理论来寻求Petri网活性的充分条件，避免遍历可达图，有效地降低计算复杂度.

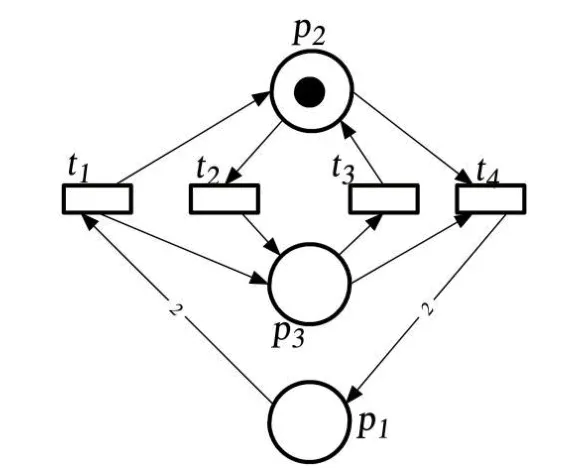
图3 例2的Petri网系统

7 Petri网活性的判定

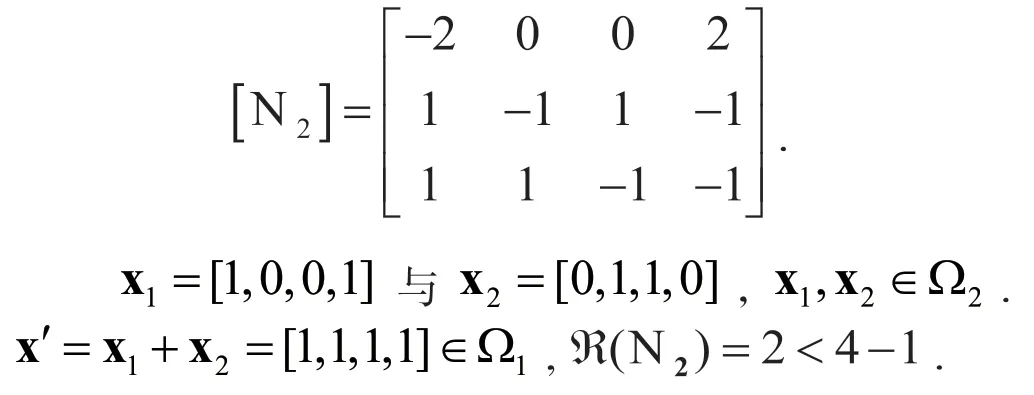
对于关联矩阵增加的行[−1,1,0,0]，[0,0,−1,1]，在有界时确保增广网系统有界，向关联矩阵再添加一行[1,−1,0,0]，[0,0,1,−1]，得到矩阵，相当于在原Petri网系统中增加库所p4,p5,p6,p7，所示如图4.此时，矩阵A1与等价.

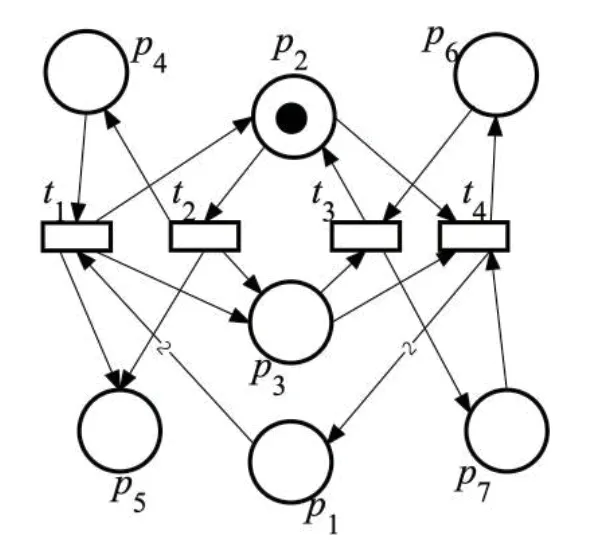
图4 例3的Petri网系统

8 结论

本文基于Petri网的状态转移方程，讨论了确保Petri网活性的充分条件与必要条件，并且将讨论的范围拓广至通用的Petri网，不限定网具有特殊结构.对于普通网（弧上的权重皆为1）成立的活性的充分与必要条件，对于通用网来说，大多数都不再成立.Siphon是一个与Petri网活性相关的关键结构.相较于大多数学者提出的可控Siphon的概念，文中提出了非前阻塞Siphon的概念，在验证活性满足的条件时，可降低计算复杂度.当Siphon生成的子网是无汇合时，提供了一个线性规划方法来判定Siphon是非前阻塞的，进一步降低了计算复杂性.在讨论保持活性的充分条件时，给弱活性添加某些约束（数学上表示为齐次线性方程组仅有正整数解），以确保Petri网是活的.最后，增加库所构造Petri网的增广网，通过增广网的行为逼近原网的行为，从而判定原网的活性.在此要求增广网的活性容易验证.弱活的判定可借助于非前阻塞Siphon来完成.

据作者所知，当前文献中提出的Petri网活性判定方法有：不变量控制、Trap控制、最大最小可控Siphon等.在这些常用方法失效后，本文提出的方法仍然适用，有兴趣的读者尝试文中的例3.因此，理论上，本文提供了另外一条途径处理Petri网活性问题.

本文还有一些未完成的工作.在判定非前阻塞的时候，限定了子网是无汇合.对于有汇合的子网还未能给出判定方法.理论上，我们只要求满足条件的增广网存在即可，但基于原网构造增广网方法也具有技巧性.这些成为我们下一步的工作.