基于大、小变形理论的钢筋调直机结构参数优化

朱晓岩，张世邦，李颂华，魏 超

(1.沈阳建筑大学工程训练中心，辽宁 沈阳 110168；2.沈阳建筑大学机械工程学院，辽宁 沈阳 110168)

调直机是一种常见于建筑施工场所的工程机械，应用最广泛的是平行辊式调直机。调直工艺经上百年的理论研究和实验验证，在调直方案上有大压弯变形理论和小压弯变形理论，对于不同种类和应用场合的工件，都有了相应的调直办法。以前采用的调直方案都是一步反弯调直，即大、小压弯变形理论的单独应用，但随着现代材料强度的提高和调质处理的广泛使用，也给调直工艺提出来更高的要求。V.N.Shinkin[1]建立了新的调直辊下压量的近似算法；杨会林等[2]通过研究得出使用大压弯变形时过大的反弯对于调直并没有好处；崔甫等[3-4]对大、小压弯变形理论和应用做出了深入的分析并提出三步反弯调直理论；郑夕健等[5]以小压弯变形探究调直机不同压下量对工件调直力的影响；万先松等[6]研究了大压弯变形理论并制定了精确的调直规程。

在钢筋塑性变形理论中有两种理论是相对被大家接受的，塑形大变形和塑形小变形理论是钢筋塑形变形调直理论中两种不同的塑形回弹情况。大变形理论消除曲率的过程为先对某一方向进行大的压下弯曲，再反向缩小弯曲，最后统一整体曲率；当使用比较小的弯曲率来压弯钢筋时，并且根据调直方程计算每次反向弯曲曲率比,小变形理论认为钢筋在调直过程中的整体曲率不均匀,小变形理论的压弯曲率比按初始曲率或残余曲率比的大小计算，消除了钢筋的反向弯曲，但钢筋的弯曲方向不均匀，残余曲率接近消失，保证了残余曲率的进一步减小[7]。

在近些年来的钢筋调直实践证明，对于横截面不规则的钢筋，更适用于大变形理论；对于截面规则的圆棒材，更适用于小变形理论。但是二者之间存在着一些不足。小变形理论与大变形理论相比，对钢筋的压弯次数需求更多，这就会造成加工硬化；大变形理论中，钢筋结构由于受到反向弯曲变形的作用会被毁坏，甚至产生裂痕，严重影响使用性能。所以，根据不同钢筋的实际情况，可以采取不同的调直方法。

基于上述分析，笔者研究异辊距钢筋调直机结构参数对调直的质量和加工性能的影响，选定方案是将上述两种变形理论在不同的调直阶段中组合应用，就是在调直初期应用大变形理论，进行大变形调直，在调直后期采用小变形理论进行调直；辊系是排列方式是大辊径调直在前，小辊径调直在后，这种排布方式既可以对前几个辊子产生的冲击力进行缓冲，避免出现需要经常更换辊子的情况，又可以减小出口的空白矫直区和残余变形。研究表明：这两种理论互相融合的实施方案，解决了不同辊子受力不相等的困难，并且总的调直力也大为减小。

1 异辊距调直机基本结构参数的计算

1.1 异辊距调直机辊数的选取

调直件应用的是截面为圆形没有肋的HRB400E钢筋。钢筋两侧变形是镜像的，初始相对扭矩比为5。在大型轧辊弯曲前，两侧的弯曲快速同向化，残余量趋于一致，大辊的辊数也是通过前向函数来计算的。钢筋产生大压弯变形之后，进入后面的小辊径辊组进行调直，调直质量将会进一步提高。小辊径组的辊数可以由钢筋的挠度决定得出。异辊距调直机调直过程示意图如图1所示。

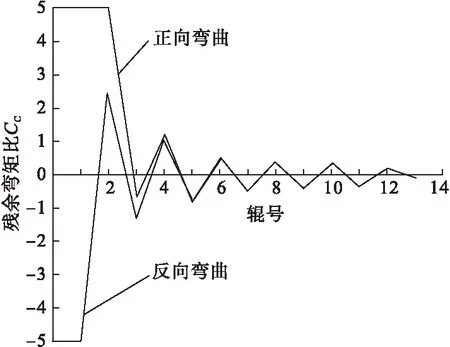
图1 异辊距调直机调直过程示意图

调直机前面的大辊径辊组调直原理采用大变形理论，弯曲率比为1.678 7是由小变形理论计算得来的，大压弯量应该选取比上述取值更大的值，但是取值也不宜过大。由于调直件应用的是截面为圆形没有肋的HRB400E钢筋，压弯比率取值为3～5[8-9]。

调直机后小辊径辊组的矫直原理采用小变形理论，当弹复曲率比与反弯曲率比之比相等时，对钢筋进行矫直。钢筋的调直公式为

(1)

式中：C0为原始曲率比；Cw为反弯曲率比。

当式(1)中对应于不同Cw的Cf的大小为C0=0时，通过将计算出的Cf替换为CC=Cw-Cf，可以得到残余曲率比。

由此计算得出：10次反复弯曲后，钢筋达到调直精度的要求，残余曲率为0.018 4，残余挠度为0.144 mm/m。在实际工作条件下，压下调整装置和辊子直径对调直机中每个辊子的压力都有一定的影响，通常会增加一个或两个辊子，以减少理论与实际的偏差。

笔者共使用了13个工作辊，即6台在上一排(可单独调节至较低的压力)，7台在下一排，理论残余挠度为0.642 mm/m。表1为调直过程中各辊处钢筋残余弯矩比情况。

表1 调直过程中各辊处钢筋残余弯矩比

1.2 辊径计算

选取调直辊的辊径时要同时斟酌进给物的咬入条件和调直辊下工件的接触强度。调直所需的压弯曲率Aw要比弹性极限曲率大很多。Aw的增加与工件的原材料和断截面形状的形状有关。例如：集中在工字形或管形类断面的金属材料的数值范围为1.1～2。因为Cw的曲率比值等于压弯曲率除以弹性极限曲率At，即用于调直曲率的倍数。总之，当已知Cw(压弯曲率比值)时，能得出Aw的负一次幂就是所需调直辊的半径：

(2)

式中：R为调直辊半径，mm；Aw为压弯曲率；Cw为压弯曲率比；At为弹性极限曲率；E为材料的弹性模量，MPa；H为材料的直径，mm；σt为弹性极限，MPa。

调直辊直径为

(3)

式中：D为调直辊直径，mm。

为方便起见，采用了单位厚度辊径值dH=D/H的方法。

从钢筋材料来看，钢筋材料对Cw的取值有影响，其强度、强化特性越高，其值越大。当工件厚度H<0.5 mm时，辊径D很小。辊径过小，对机架结构安排有很大的影响，因为如果辊径过小抵抗冲击的能力越低。由此可知，调直辊径采用过小的尺寸，调直的效果越好。但是对于辊式调直机来说，要调直尺寸特别小的工件是不可能完成的。钢筋弹性模量E=206 000 MPa，矫直时抗弯模量较大的Cw=4，矫直该工件所需的最大单位辊径值可在dH=206 000/σt=51 500/σt时求解。

在调直过程中，由于变形量较大，所以容易造成压下率不稳定而导致带钢跑偏。为了避免这种情况发生，必须对调直机进行改进。可以把钢筋调直模型简化成调直的是圆柱面和平面，并用接触应力来限制调直辊的辊径，参见式(4)。

(4)

根据对钢筋咬入情况的分析，钢筋咬入模型如图2所示。钢筋可以成功调直的条件：

图2 钢筋咬入模型

Fx+Px>Nx.

(5)

式中：Fx为下辊送进力；Px为上辊咬入摩擦力P水平方向的分力；Nx为上辊推出力水平方向的分力。

根据受力平衡条件可知y方向有

Fy=Ny+Py=Ncosα+μPsinα.

(6)

式中：调直辊和钢筋法向压力分别为N、Fy，Py为上辊咬入摩擦力P水竖直方向的分力，咬入角为α，接触面的摩擦系数为μ。

由图2可知，Fx=μFy，P=μN，Px=μNcosα，Nx=Nsinα。咬入条件为

μFy+μNcosα>Nsinα.

(7)

将式(6)代入式(7)整理得

2μcosα+(μ2-1)sinα>0.

(8)

式中：μ为调直辊面与钢筋表面的滑动摩擦系数，μ=0.2。由图2咬入模型几何关系可知，cosα=(R-e)/R；sinα=(2Re-e2)1/2/R；e为上调直辊的压下量，设定e=3.3485σtR2/EH，mm；代入式(8)中得出：

R2-13.52Re+6.76e2>0.

(9)

解得：

根据以上计算，单位厚度辊径值是选择辊径的重要依据。需要矫直的工件是一根直径为8～12 mm的HRB400E型钢筋。众所周知，最终将计算出的σt=400 MPa，将辊径从112 mm矫直为185 mm。初步选择辊径,大型卷材为160 mm，小型卷材为120 mm、125 mm和130 mm。比较这些不同的小辊组，得出了不同辊径对调直机工作质量的影响。

1.3 辊距的计算

辊距与辊径的关系用t=aD表示，其中a值在调直辊中为1.2，而在整体下压中为1.1。

(1)最大允许辊距：辊距过大，难以满足调直所需的弹塑性变形，容易滑移，发生这种情况的话，可以理解为钢筋不能进入调直辊；最大辊距应综合分析调直质量和咬入条件，取两个值中较低者为最大辊距上限。

因此，钢筋必须弯曲至相当于最大原始曲率的1/Pf的最大弹复曲率，其中Pf=EI/Ms(Ms为塑性弯曲力矩，Ms=σsd3/6；i为惯性矩I=πd4/64)。为保证足够弯曲程度，必须满足1/2(D+d)≥1/Pf(D为调直辊直径，d为钢筋直径)，修改后的Dmax=2Pf-d=2EI/Ms-d。由于设备和技术的限制，在实际生产中难以实现上述要求，需要对原计算公式进行修改，以便更准确地计算出最佳辊系结构参数和相应尺寸系数。最后，笔者通过对试验数据进行拟合，得到了在不同工作条件下的最佳压下量公式。tmax=a(2EI/Ms-d)(a=1/β,即直径与辊距辊径的比率)。

从t=aD的辊距与辊直径之间的数量关系中推断出，调整后的最大辊距tmax=βEd/19.2σs。

(2)最小允许辊距：当钢筋直径一定时，调直机辊间距越小越好；若要达到最大限度地降低挤入量，则必须保证调直机辊距取为最小值。要是调直辊径太小的话，钢材表面的局部压力就会很大，这样就加重辊面的磨损情况，钢筋就有划伤和压痕。

(10)

式中：μ1、μ2为钢筋与调直辊之间的摩擦系数，μ1=μ2=0.2；d为钢筋直径，mm；P0是最大许用应力，P0=2σs。

(11)

式中：Fmax为调直辊在钢筋上的最大挤压力，N；k0max为钢筋最小弹性和厚度系数，k0max=0.3；W为钢筋的弹性断面系数，mm3；η为钢筋强化系数，η=0.1。

将式(11)代入式(10)中，辊距tmin≥7.15d。经计算，调直辊辊距为86～178 mm。

1.3.1 辊距的优化

将参数优化应用到机械设计中，这样问题就是以总调直力最小为目标在辊距范围内寻找最优的辊距。

(12)

式中：Fi(i=1，2，…，n)为各调直辊处的挤压力大小，N；Mi为各调直辊处钢筋弯曲力矩，kN·m。

调直辊的挤压力可以通过调节弯曲钢筋所需的调直力矩来计算[10]。笔者提出一种简便计算调直辊所受挤压力的方法，将调直模型简化为具有集中载荷的连续梁，辊子在钢筋上作用的调直力相当于集中载荷。弯矩值原始曲率与反弯曲率有关，但很难计算。可将异辊距调直机每卷钢棒的钢筋弯曲力矩[11-12]简化为：

(1)2、3、4、5号调直辊上的钢筋产生纯塑性变形，即M2=M3=M4=M5=Ms。

(2)钢筋在10、11、12号调直辊上相当于纯弹性变形，即：M10=M11=M12=Mw。

(3)除1号和13号辊外，其余调直辊的钢筋弯曲力矩为M6=M7=M8=M9=Ma=1/2(Ms+Mw)。

钢筋的塑性弯曲力矩：Ms=σsS。

钢筋的弹性弯曲力矩：Mw=σsW。

钢筋塑性截面系数：S=d3/6。

钢筋弹性截面系数：W=πd3/32。

计算直径为12 mm的HRB400E钢筋的系数和弯矩：塑性弯曲力矩Ms=115 200 N·mm；Ma=91 529 N·mm；弹性断面系数为W=169.65 mm3；弹性弯曲力矩Mw=67 859 N·mm；塑性断面系数S=288 mm2。

1.3.2 约束条件

根据辊距的配置原则，入口辊距遵循从小到大的布局。这种结构可以避免钢筋咬入时与钢筋接触，促进钢筋的成功进入。中间部分的辊距要大，出口端的辊距与入口端成镜像排列。首先，建立方程的约束条件，将辊距之间的关系限制为方程组(13)。

(13)

式中：xi(i=1，2，…，12)为调直部分的辊距代号；hi(i=1，2，…，12)均为方程序号。

建立一个不等式的约束条件,以限制辊距的范围。如方程(14)中所示，式中：xi(i=1，2，…，12)为辊距代号；gi(i=1，2，…，12)均为方程序号。

(14)

在MATLAB中使用fmincon函数对辊距进行参数优化。多次调试后改变搜索的初始值，结果保留到小数点两位，误差较小。结果表明，所得结果是全局最优解。最终的辊距如表2所示。

表2 优化后的辊距

优化前后各辊受力情况如图3所示。结合折线图分析和计算结果可以看出，除了开始端和末端1号和13号调直辊受力明显小外，2～5号调直辊受力较大，6～12号调直辊受力较小。结果表明，调直辊受力更加均匀，调直过程趋于稳定。

图3 各辊优化前后受力情况

1.4 辊 长

调直辊的长度与调直辊两端与孔型之间的结构余量有关。此外，还与钢筋的宽度和孔数有关。辊长公式为

L=nBmax+(n-1)b+a.

(15)

式中：n为孔型(槽)数；Bmax为工件的最大宽度，mm；b为孔型间的结构余量，b=(0.1～0.3)Bmax，mm；a为辊端的结构余量，a=(0.2～0.6)Bmax，mm。

笔者设计的调直辊为单孔型。调直辊的长度计算为12.8～19.2 mm，矫直矫直辊长度计算为19 mm并考虑到接触强度。

2 调直速度

随着钢筋调直机的发展，调直速度有了很大提升。从原来的10 m/min低速加工到180 m/min以上的高速加工。根据实际经验，为了确保加工材料有充足的弹性形变，加工时，调直速度应低于加工材料形变速率[13]。对于原始曲率、屈服强度和直径较大的钢筋，应该采用低速调直。而对于原始曲率、屈服强度和直径较小的钢筋，应采用高速调直，这样既能缩短加工时间又可以获得不错的调直效果。实验钢筋HRB400E型属于Ⅲ级钢，应在较低的转速下调直。反之可选用高速调直，以避免因塑性变形不完全而产生断丝现象。为了获得精确的调直速度，每个调直辊都由不同的电机驱动。据市场上现有钢筋调直机的研究[14]，钢筋调直机加工速度在0.6～3 m/s。

在其他条件不变的情况下，只有改变车速，即1.2 m/s，才能达到最好的矫直调直效果。在3 m/s时调直精度调直速度提高了12.3%。通过建立不同参数下大、小两种轧辊组轧制的有限元模型，分析了各种工艺参数对前、后鼓形量和轧件厚度分布的影响。通过试验验证，仿真结果如图4所示。当调直速度到1.2 m/s时，大辊前轮的角速度为15 rad/s;小辊后轮的角速度为20.87 rad/s(Φ115 mm)、20 rad/s(Φ120 mm)、19.20 rad/s(Φ125 mm)、18.46 rad/s(Φ130 mm)。

图4 不同调直速度下钢筋的平直度情况

3 模拟仿真

3.1 模型建立与设定

在分析调直过程之前，先简化模型。由于仿真是为了便于查看演示调直过程和调直结果，因此只关注调直辊与钢筋接触情况，简化调直过程。调直辊被认为是生产线的中心对称性，可以实心辊辊空心圆筒滚筒，以减少模型中网格数量并加快运行时间。

在整体模型网格密度的设定上，为了更加与实际生产相吻合，网格划分质量的平均值小于0.4。笔者研究的重点是后辊组辊径尺寸对钢筋调直精度的影响，将调直辊视作不变形的刚体，在网格划分时密度相对较小，不影响整体结构形状即可；在对钢筋进行网格划分时采用较大的密度。

边界条件设定：模型中已在调直位置的钢筋是不存在弯曲的，取正中间的一个面作为位移的零点；各个辊子定义为刚体材料并进行位置约束：即各个辊子在X，Y，Z方向的位移约束和绕Y轴的旋转约束；根据仿真模型钢筋的弯曲程度，通过理论计算并结合实际加工经验设定上排辊的压下量如表3所示。

表3 调直机上排辊的压下量

3.2 仿真结果分析

采用ANSYS Workbench中瞬态分析模块进行仿真，调直前钢筋形状如图5所示。

图5 钢筋调直前形状

前辊参数不变的情况下，后辊组的辊径分别为115 mm、120 mm、125 mm、130 mm，调直效果见图6所示。在其他条件相同的情况下，后辊组辊径为125 mm时，调直效果优于其他组。

图6 各辊径的调直情况

调直标准后可实现钢筋的挠度Δ<1 mm/m。 首先，在矫直前将进入矫直段的钢筋(这段钢筋是笔直的，钢筋中间段作为零位移参考面，由于此段钢筋并没有完全经过调直处理，所以钢筋处理后不笔直是正常现象)。当后辊组的辊径为125 mm时，调直挠度低于标准要求的挠度，钢筋的平均残余挠度为0.643 mm/m。当后辊组的辊径为115 mm时，矫直钢筋的钢筋残余挠度为0.77 mm/m，虽然符合标准，但与后辊组的辊径为125 mm相比，调直效果稍有下降。因此，后辊组辊径尺寸对于调直效果有着重要影响。

4 结 论

(1)在矫直速度和压下量相同的情况下，后辊组辊径越小，钢筋调直效果越好；为了在调直过程中提高接触面的稳定性，在调直精度差异较小的情况下，选择后辊组辊径相对较大；后辊组辊径Φ130 mm调直后的钢筋残余挠度均值为0.665 mm/m，调直效果虽没有后辊组辊径Φ125 mm理想，为提高调直过程中的稳定性，应优先选择后辊组直径Φ130 mm的调直结构。

(2)根据矫直钢筋的残余挠度与矫直钢筋钢筋，后辊组辊径的残余Φ125 mm可以减少16.49%；为了得到最佳的调直效果，有必要采用二分法，在合理的范围内进行优化；通过对二次、三次以及四次仿真所得数据进行比较分析可以看出：当模型中参数取不同值时，其得到的调直效果也不尽相同，所以选择适当的参数是很重要的。