下弦开敞桁式波形钢腹板组合箱梁桥施工过程的力学分析

吴丽丽，邹 悟，耿大林，于雅倩

(中国矿业大学(北京)力学与建筑工程学院，北京 100083)

波形钢腹板组合箱梁桥由于具有结构形式合理、造型美观、自重轻、经济性好等优点，被广泛用于大型桥梁工程中。波形钢腹板组合箱梁桥采用轻薄的波形钢腹板替代了普通混凝土箱梁中厚重的混凝土腹板[1]，显著降低了结构自重，大大减少了现场湿作业量。邓强民等[2]运用有限元正交数值模拟来分析大跨钢桥桥面铺装有限元分析简化模型，提出纵边自由，横边简支，横隔板底固结约束的简化模型。冀伟等[3]提出了一种结合Fmincon算法和响应面法的适用于波形钢腹板组合箱梁桥的有限元模型修正方法。L.M.Tian等[4]提出了模拟大跨度刚性钢结构施工过程中结构行为节点修正的单元生死法。叶智武等[5]将每个施工阶段分为初始时刻和结束时刻进行分析，提出了结构刚度矩阵修正的新方法以及修正设计位形定位法。关于桥梁施工工艺和过程模拟分析， M.F.Granata等[6]通过在曲线梁桥中采用转换矩阵的方法来对其顶推施工进行数值分析。姚红兵等[7]采用有限元软件对波形钢腹板组合连续刚构桥的自承重施工过程进行了模拟。刘旭政等[8]通过有限元分析得到荷载类型对波刚腹板组合箱梁桥影响较大。许世展等[9]发现波形钢腹板组合梁桥悬臂施工下悬臂根部顶板应力分布最不均匀。王春江等[10]通过有限元建立精细梁杆模型对钢箱梁悬索桥施工阶段的稳定承载力进行了分析。D.WANG等[11]对波形钢腹板组合箱梁桥的新型异步悬臂施工全过程进行了模拟。一种新型的下弦开敞桁式波形钢腹板组合梁桥[12]，将传统的混凝土底板置换为方钢管开敞桁式下弦，避免了下部受拉翼缘混凝土裂缝外露等问题。针对下弦开敞桁式波形钢腹板组合梁桥，笔者采用空间梁系模型，对比T构-单悬臂连续施工、逐跨连续悬臂施工和顶推施工3种施工方法对桥梁施工过程受力性能的影响，并从中选取最优的施工方法进行体系转化状态分析和典型施工阶段的局部三维精细模型分析。

1 3种桥梁施工方法对比

1.1 有限元建模

考虑到桥梁较长、施工工序较多，若建立实体模型，单元划分的工作量大，计算耗时长，所以仅采用空间梁系单元进行建模，并将结构视为统一的混凝土材料。

在组合箱梁桥的有限元模型中，主梁和钢导梁选用空间三维有限应变梁单元BEAM188，异形截面采用PLANE82单元模拟；利用ANSYS中单元生死功能，在求解中根据施工方法和施工过程的不同阶段定义载荷步，随着施工的行进，激活相应梁单元，设置对应约束与力，固定支座约束所有自由度，简支支座约束X轴和Y轴的平动自由度以及Y轴的转动自由度。

3种施工方式采用同一截面和跨径，模型中采用等截面三跨连续组合箱梁桥进行3种施工方式的对比模拟，桥梁全长48 m+80 m+48 m=176 m，桥梁截面如图1所示。模型统一采用C50混凝土材料进行模拟。

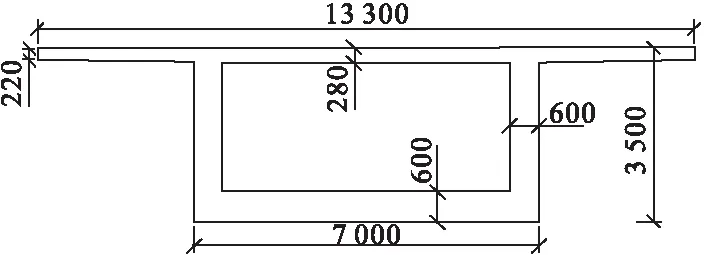
图1 桥梁截面图

计算模型每1 m划分一个单元，悬臂施工共计划分为176个单元，顶推施工为208个单元，有限元模型如图2所示。

图2 有限元单元分布图

1.2 施工段划

1.2.1 T构-单悬臂连续施工

T构-单悬臂连续施工的施工顺序如图3所示。从B墩开始进行悬臂施工；A端岸跨边段2合龙，释放B墩临时固结，形成单悬臂梁；C墩进行悬臂施工；D端岸跨边段4合龙，释放C墩临时固结形成单悬臂梁；BC跨中段5合龙，形成3跨连续梁结构。

图3 施工顺序图

T构-单悬臂连续施工的施工过程模拟为46个施工阶段(见图4)。 施工阶段1～18分别为0#～9#块的依次施工；施工阶段19～21为左边跨现浇段施工及合龙(支座转换)；施工阶段22～39分别为10#～19#块的施工；40～42为右边跨现浇段施工及合龙(支座转换)；施工阶段43～45为中跨合龙(支座转换)阶段；施工阶段46为去除所有力仅留自重荷载。每个悬臂梁段的施工过程简化模拟为挂篮前移、浇筑混凝土两个阶段，必要时加入拆除挂篮阶段。施工阶段主要承受施工荷载3 000 Pa；挂篮荷载为4×105N；节段荷载为9×105N。

图4 悬臂施工节块分布

1.2.2 逐跨连续悬臂施工

逐跨连续悬臂施工的施工顺序如图3所示。从B墩开始进行悬臂施工；A端岸跨边段2合龙，释放B墩临时固结，形成单悬臂梁；C墩进行悬臂施工； BC跨中间段5合拢，释放C墩临时固结,形成带悬臂的两跨连续梁，最后进行D端岸跨边段4合拢。

逐跨连续悬臂施工的施工过程模拟同样为46个施工阶段(见图4)。 施工阶段0～39以及46与T构-单悬臂连续施工完全一致；此外的施工阶段40～42为中跨合拢阶段，43～45为右边跨现浇段施工及合龙。施工过程简化和施工荷载也与T构-单悬臂连续施工相同。

1.2.3 顶推施工

顶推施工是在桥台的后方设置施工场地，分阶段浇筑梁体，并用纵向预应力筋将浇注阶段与已完成的梁体联成整体，在梁体前安装钢导梁，然后通过水平千斤顶施力，将梁体向前方顶推出施工场地，重复这些工序即可完成全部梁体施工。顶推施工法每节段取16 m，导梁长度取跨径的2/3即32 m，临时墩的布设参考文献[13]、文献[14]、文献[15],临时墩及节段布置如图5所示。全部施工过程模拟为14个施工阶段，施工阶段1激活导梁和对应1#墩及临1墩；施工阶段2激活主梁1和2#墩；施工阶段3～11依次激活主梁2～10和对应墩；施工阶段12拆除导梁，激活主梁11；施工阶段13拆除临时墩；施工阶段14为支座转换。

图5 临时墩及节段布置

1.3 3种施工方法的计算结果对比

1.3.1 竖向变形对比

竖向变形的控制是多跨连续箱梁桥悬臂浇筑施工至关重要的任务之一(见图6)。对比悬臂施工和顶推施工全过程位移可以发现，对于悬臂施工，在T构悬臂施工阶段0～20，随着施工阶段的进行，竖向位移逐渐增大，悬臂施工过程中最大位移皆在50 mm以上，主要出现在T构施工的悬臂端附近；而顶推施工过程中主梁与导梁向前推进时，最大位移维持在5 mm以内，变化幅值不大。从支座转换来看， 顶推施工法挠度值相较悬臂施工变化较大，这是因为去除临时支座，结构由八跨转变为三跨，故最大位移突然增大；支座转换时，中间两支座变为铰接，位移进一步增大，故支座的拆除以及支座的转换对主梁变形会产生较大影响。

图6 施工位移图

1.3.2 弯矩对比

表1为悬臂施工的最不利内力表，表2和表3分别为顶推施工过程中导梁和主梁的最不利内力表。由表1～表3可以看出，从施工过程中内力变化的角度看，悬臂施工最大弯矩主要出现在2#、3#墩(见图5)，最大弯矩值介于197 410～228 200 kN·m；顶推施工过程中，构件的弯矩随梁体前进不断交替变化，最大弯矩出现在导梁上，为100 640 kN·m，主梁弯矩介于6 352 ～11 239 kN·m，远小于悬臂施工过程的最大弯矩。从支座转换来看，T构-单悬臂连续施工支座转换前后的最大弯矩值最大，前后分别为197 410 kN·m、227 240 kN·m，而顶推施工最小，最大弯矩值由136 860 kN·m变为115 850 kN·m。

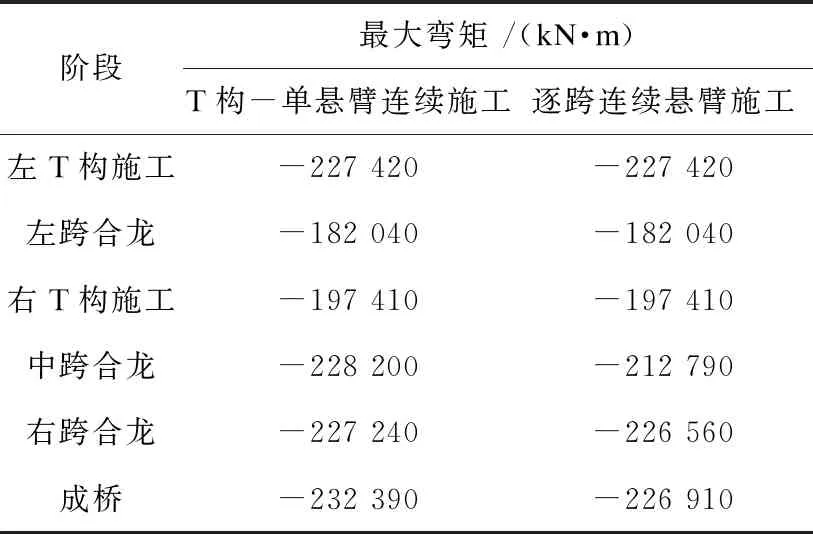
表1 悬臂施工弯矩

表2 钢导梁顶推最不利内力

表3 主梁体系转换内力变化

1.3.3 剪力对比

表4和表5为悬臂施工过程和顶推施工过程剪力计算结果。从剪力大小来看，悬臂施工最大剪力主要出现在2#、3#墩，在9 862～11 045 kN变化。顶推施工过程主梁最大剪力为3 065 kN，约为悬臂施工的四分之一。从支座转换前后变化来看，悬臂施工和顶推施工的最大剪力变化差距不大，最后均为10 726 kN。

表4 悬臂施工剪力

表5 顶推施工最大剪力

通过对比T构-单悬臂连续施工、逐跨连续悬臂施工和顶推施工过程中的竖向位移和内力变化，表明顶推施工除支座转换时挠度值相较悬臂施工变化较大，在施工过程中，顶推施工整体的弯矩、剪力以及变形较小。故采用顶推施工法对组合箱梁桥做进一步施工模拟。

2 顶推施工过程结构体系转换分析

2.1 施工阶段划分

利用顶推施工法梁系模型进行进一步分析整个施工过程节段划分(见图5)。笔者设计每顶推4 m为一个工序，共计47个工序。工序1导梁就位悬出，工序2到45为推进梁段和导梁悬出的过程，工序46拆除临时墩，最后的工序47成桥。

2.2 支反力分析

支反力在施工过程中是各千斤顶推施力的主要依据，同时影响着钢箱梁局部受力。顶推施工过程中的1#墩、临1墩、2#墩、临2墩、临3墩(见图5)参与顶推施工的工序较多，故取这5个墩的墩顶支反力做顶推全过程反力曲线(见图7)。从图可以看出，各墩顶的支反力变化趋势一致，随着梁体与墩顶支座的接触，支反力逐步增大，直到新的支座开始参与受力，支反力开始减小，并维持在稳定数值。除前期主梁、导梁刚与墩支座接触时变化幅度大，其他支点的支反力大小为3 198.43～6 396.85 kN。拆除临时墩时，1#、2#墩(见图5)支反力大幅增大，但增大后的反力值仍小于最大悬臂状态时的支反力。此外，各顶推施工阶段，各钢箱梁支点未出现负反力，这说明施工过程中各支点没有出现脱空的情况。

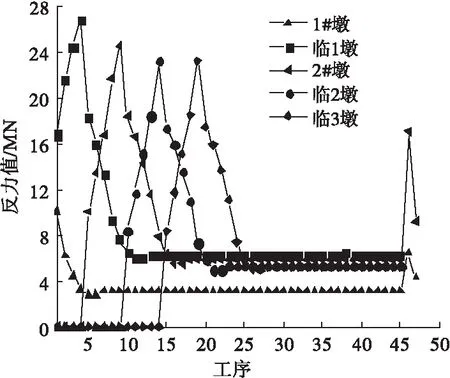
图7 顶推全过程反力曲线

2.3 体系转换过程中的受力分析

拆除导梁时主梁前端与导梁连接处的受力将会发生变化，弯矩状态变化如图8所示。导梁的拆除和支座约束转换对桥梁整体受力的影响较小，临时墩的拆除，使桥梁由八跨连续梁变为三跨，对梁体受力影响较大，2#、3#支座负弯矩由1 199.4 kN·m增大至106 470 kN·m。剪力受体系变化的影响与弯矩类似，导梁的拆除对体系影响较小。临时墩拆除后1#墩和4#墩剪力值增大，由3065.2 kN增大至6 263.6 kN ，变为原来的两倍，2#墩和3#墩剪力值也增幅较大，由25 321 kN增大至105 280 kN ，为拆除前的4倍。

图8 弯矩状态变化图

从图8可知，在体系转换的过程中，导梁的拆除对体系影响较小，临时墩的拆除影响较大，临时墩拆除前后主梁弯矩、剪力成倍增大。

3 下弦开敞桁式波形钢腹板组合箱梁桥施工过程的局部受力

3.1 建立有限元模型

桥梁结构设计为等截面三跨连续梁(见图9)。采用ANSYS建模，其中混凝土板和钢管内混凝土采用SOLID95单元模拟，上翼缘钢板、波形钢腹板和矩形钢管则采用SHELL181单元模拟，桁架和预应力筋分别采用BEAM188单元和LINK8单元模拟。混凝土材料为C50，除桁架选用Q345钢外，其余钢结构构件均选用Q235钢。

图9 截面尺寸示意图

钢材本构关系采用理想弹塑性模型，混凝土本构关系采用Hongnestad提出的混凝土单轴受压应力-应变本构关系曲线[16]。模型中混凝土顶板与下部矩形钢管内混凝土单元划分尺寸为0.8 m，腹板网格划分采用自由网格划分，为规则的四边形单元，上翼缘钢板与下翼缘钢管采用映射网格划分为规则四边形单元，预应力筋采用体分割法划分。

当结构处于最大悬臂状态时为最不利工序，由于悬臂20 m时的情况较少，且此时仅主梁顶推12 m，长度较短，所以笔者以工序9(顶推至32 m时，悬臂16 m)和下一个工序10(顶推至36 m)的状态为例进行分析(见图10)。 工序9模型一端固结，一端为释放纵向自由度，而工序10模型两端边界视为固结。钢导梁与钢箱梁连接段有限元模型如图11所示。

图10 工序简图

图11 局部计算模型图

3.2 导梁受力分析

在施工过程中由于重力作用，导梁会随着工序产生挠度，挠度过大会造成导梁翘起，使导梁不能很好地与滑道接触。工序9下导梁的最大竖向挠度为 3.20 mm，位于悬臂端。10工序由于有了临2支座，最大竖向位移小于工序9，为 0.42 mm，位于桁架支撑处。两工序的最大竖向位移都小于《公路桥涵施工技术规范》(JTG/T F50—2011)所规定的5 mm。

图12为两种工序下导梁剪应力图。导梁主要受力构件为波形钢腹板，工序9的剪应力最大值为17.5 MPa；工序10剪应力最大值为1.41 MPa。两工序最大剪应力均远小于钢材容许剪应力120 MPa。

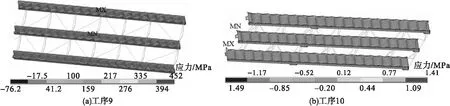
图12 导梁应力图

3.3 顶板应力分析

图13为顶板沿纵桥向应力图。从图可知，顶板主要承受压应力，工序9、工序10最大轴向压应力分别为1.03 MPa、0.81 MPa；最大轴向拉应力为分别1.48 MPa、0.77 MPa，应力水平均低于小于规范所规定的2.64 MPa。拉应力主要出现在顶板与腹板交界处以及1#支座处，这是由于1#支座处支反力的作用使其有向上挠曲的趋势而出现拉应力，腹板给顶板一定支撑，使得接触处出现小范围拉应力。

图13 顶板沿纵桥向应力图

3.4 截面应力分析

取工序9、工序10的支座截面、边跨跨中截面(见图10)，分析下弦开敞桁式波形钢腹板组合箱梁桥施工阶段各个工序下的顶板应力的变化规律。图14分别为工序9、工序10的应力分布图。由图可知，主梁截面受到根部固结条件影响，应力最大位置在1#墩处z=0 m处，中腹板与顶板交界处的应力值最大，翼板边缘和两腹板中部相对较小。除临1墩处z=24 m应力分布不均，其他位置处应力分布均匀，剪力滞影响程度小。这主要是由于临1墩处支反力的施加使得此处截面应力分布不均匀，剪力滞影响程度较大。相较于最不利工序9，工序10沿桥纵向应力数值浮动较小，除1#墩处顶板截面应力外，其他截面应力分布情况较为接近。

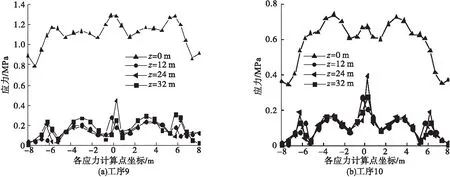
图14 不同位置顶板应力分布

4 结 论

(1)对比顶推施工、T构-单悬臂连续施工和逐跨连续悬臂施工等3种施工方法，顶推施工过程的剪力、弯矩远小于两种悬臂施工，并且顶推施工整体变形较小，因此顶推施工更适用于组合箱梁桥。

(2)在顶推施工过程中，结构处于最大悬臂状态时，墩顶支反力和导梁主梁前端挠度值达到最大；导梁的拆除对体系影响较小，临时墩的拆除对结构受力影响较大。

(3)顶推施工最大悬臂工序下，导梁前端挠度变形最大3.20 mm，应力最大截面位置在主梁根部固结处，除临1墩处由于支反力的施加使得应力分布不均现象明显，其他位置处应力分布均匀，剪力滞影响程度小。