近场爆炸作用下比例距离参数对抗爆间室结构可靠度的影响分析

李 闯，徐自强，王丽娟，时小凡

(1.沈阳建筑大学交通与测绘工程学院，辽宁 沈阳 110168;2.中煤科工集团沈阳设计研究院民爆所，辽宁 沈阳 110015)

抗爆间室[1]用于存放炸药，主要为钢筋混凝土墙板结构，双面配筋保证结构具有良好的延性和抗剪性能。抗爆间室内的炸药一旦发生偶然爆炸，引起的峰值瞬时压力对结构表面产生强力冲击，爆炸后需要对结构进行评估。《抗爆间室结构设计规范》(GB 50907—2013)仅通过抵抗爆炸次数将抗爆结构分为3级，既有评价方法没有考虑炸药质量、爆心距离和结构尺寸等因素，评价方法过于简单。作用于抗爆间室结构上的爆炸荷载容易受到现场温湿度、构件形状及材料属性等影响，具有明显不确定性，使结构响应与破坏形式呈现出显著的概率特性[2]。可靠度[3]定义为“结构在规定的时间内，在规定的条件下，完成预定功能的概率”。在可靠度理论的指导下，可定义抗爆间室可靠度为“在抗爆间室结构设计基准期内，通过规范地设计与施工，抗爆间室抵抗爆炸作用并正常运营的概率”，对此，抗爆间室的结构性能可以采用可靠度指标进行评价。王英等[4]考虑爆炸荷载引起的材料应变率效应，提出了爆炸冲击下的材料强度设计方法。李忠献等[5]考虑材料性能、爆炸效应和构件尺寸不确定性的影响，提出钢梁结构在不确定爆炸荷载下的可靠度计算方法。H.Y.Low 等[6]采用数值模拟的方法计算了爆炸冲击下混凝土单向板的弯曲变形，得到了混凝土板的失效概率与爆炸荷载正超压的函数关系。M.Soares 等[7]基于响应面方法计算材料强度的概率函数，分析板架结构可靠性的影响因素。在爆炸荷载作用下，结构尺寸、材料属性甚至模型的不确定性[8-9]，反映结构爆炸过程的随机属性。比例距离[10-11]指爆炸中心距结构的最小距离和炸药质量立方根的比值，是影响爆炸冲击下墙板结构失效的重要参数。笔者选取钢筋混凝土板为研究对象，进行爆炸冲击下的结构响应[12-13]计算，通过统计分析方法，考虑材料强度与构件尺寸的随机属性，提出爆炸冲击作用下的比例距离参数对墙板结构可靠度影响分析，得到板失效概率-比例距离关系曲线。

1 数值模型

1.1 材料模型

1.1.1 混凝土材料本构模型

采用LS-DYNA有限元软件进行数值模拟。混凝土选用改进K & C混凝土本构模型，本构模型由M.Alex 等[14]提出，是根据伪张量材料模型发展而来，提高了数值模拟软件的计算性能。混凝土材料本构关键字为Mat_072R3，混凝土参数如表1所示。

表1 混凝土参数

采用欧洲混凝土规范CEB的推荐公式[15]，x轴的正值为抗压强度动载增大系数CDIF、负值为抗拉强度动载增大系数TDIF，计算式为

(1)

(2)

式中：fdt为混凝土动态抗拉强度；ft为混凝土静态抗拉强度，logα1=7.112δ-2.33。

材料损伤[16]本构的关键字为Mat_072R3，具体公式为

(3)

式中：δ为损伤标量，当0≤δ<1，材料单元处于强化阶段；当1≤δ≤2，材料单元处于软化阶段；λm为极限强度面上修正的有效塑性应变;λ为修正的有效塑性应变，为有效塑性应变和应变率增大系数的函数作为混凝土单元失效判据。

1.1.2 钢筋材料本构模型

钢筋采用双线性弹塑性模型[17]，该模型对模拟钢筋的弹塑性阶段具有良好作用，包括等向强化、随动强化效应等。钢筋本构关键字为Mat_003，钢筋参数如表2所示。

表2 钢筋参数

钢筋的应变率效应采用Cowper-Symonds模型进行计算，屈服强度动载增大系数DIF计算式为

(4)

式中：C、P为Cowper-symonds应变率影响系数，C=40，P=5.5;ε′为钢筋应变率。

屈服强度动载增大系数DIF采用M.Alex[14]提出的方法计算，关键字为Mat_003，其本构自带应变失效准则，失效应变为0.12。

1.2 计算模型

2 结构响应

2.1 结构变形

图1为不同比例距离下的板在爆炸冲击下的损伤云图。

图1 不同比例距离的损伤积累云图

2.2 板跨中位移响应

2.2.1 跨中位移时程

图2为不同比例距离下的结构位移响应曲线。在爆炸冲击作用下，由于拉伸波作用，在板结构的背爆面，导致混凝土板产生拉伸变形，位移为负。混凝土板产生极限变形，所需时间为30 ms左右，随后结构开始回弹，做往复自由振动，结构背爆面处于受拉-受压往复受力状态。如果混凝土板的峰值位移小于弹性极限位移，混凝土板为弹性变形，最终位移为0；如果混凝土板的峰值位移大于弹性极限位移，弹性位移可恢复，最终位移响应为塑性变形，塑性变形和最大变形的差值为弹性极限位移。从图2跨中位移时程曲线可知，在爆炸冲击的作用下，混凝土板已经产生塑性变形。

图2 不同比例距离下的跨中位移时程曲线

2.2.2 跨中最大位移和塑性位移

图3 不同比例距离的跨中最大位移和塑性位移曲线

3 可靠度计算

3.1 随机变量

表3 随机变量及分布特征

根据《抗爆间室结构设计规范》(GB50907—2013)，采用位移延性破坏准则，建立功能函数：

(5)

式中：g为功能函数;u为容许延性比限值;ymax为最大位移;ye为屈服位移或者塑性位移。

可靠指标为

(6)

式中：β为可靠指标;μz、μR、μS分别为功能函数均值、抗力变量均值、荷载变量均值;σz、σR、σS分别为功能函数标准差、抗力变量标准差、荷载变量标准差。

采用蒙特卡洛取样方法，结构失效概率Pf计算为

(7)

其中，

(8)

式中：Pf为失效概率;nf为完成预定功能的样本数量;N为样本总数;I[g(xi)]为指示函数。

3.2 概率密度分析

考虑爆炸荷载、构件尺寸及材料强度的不确定性，计算结构的延性比，将延性比功能函数指标等分为若干区间，将延性比功能函数指标计算结果落入区间，给出每个区间内的指标数据的频率密度，得到频率密度，不同比例距离下的概率密度如图4所示，概率密度函数满足正态分布。

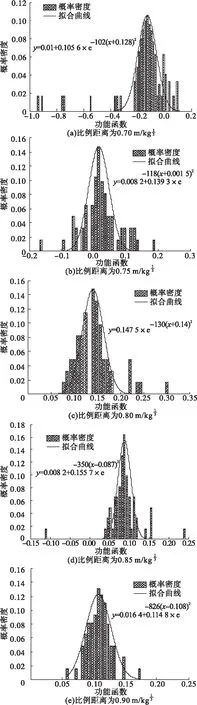
图4 不同比例距离下的概率密度曲线

表4为不同比例距离下的可靠指示与失效概率。

表4 不同比例距离下的可靠指示与失放概率

图5 不同比例距离的可靠指标与失效概率曲线关系

4 结 论

(2)比例距离越大，结构跨中最大位移和屈服位移越小，位移响应与比例距离具有非线性关系。

(4)比例距离是爆炸冲击下的结构可靠度重要指标，在工程设计中，应该对防爆结构的比例距离参数进行设计，提高结构的抗爆性能。