非线性振动声调制的混凝土梁微裂缝损伤检测试验

阎 石，崔赛杰，王 鲁，王雪南，于水旺

(沈阳建筑大学土木工程学院，辽宁 沈阳 110168)

裂缝是钢筋混凝土构件损伤中最为显著的标志，也是影响其可靠性的最主要因素之一。由于混凝土微裂缝几何体量小，检测难度大，传统基于波动分析法的损伤监测技术中的代表性参数(如幅值、波速和能量)在混凝土早期损伤阶段裂缝宽度较小甚至闭合时，并不能得到令人满意的灵敏度和精度[1-3]。

为了在混凝土结构损伤早期阶段能够达到更高的监测灵敏度和精度，非线性超声检测技术得到了广泛关注。典型非线性超声现象包括高阶谐波的产生、缓慢动力特性、非线性振动声调制(Vibro-acoustic modulation,VAM)等[4]。VAM技术由于其实现简单、信号衰减较小，更适用混凝土构件损伤检测[5]。针对非线性VAM技术的研究最早开始于20世纪90年代，并主要集中在技术理论方面[6-7]。R.P.Countney等[8-9]利用共线VAM技术对混凝土梁中的人工微裂纹缺陷进行检测。但是，压电换能器振动幅值较小，所观察到的调制效应微弱。J.P.Zardan[10]等利用非线性VAM技术重点研究了混凝土结构中裂缝所带来的非线性现象与损伤程度之间的关系，通过所建立的非线性参数与传统线性损伤识别参数进行对比，发现线性损伤识别参数在早期微裂缝发展过程中的变化并不明显。陈小佳[11]利用非线性振动声调制方法对碱骨料反应下素混凝土试件的累计损伤进行定量观测。试验结果表明，该方法对混凝土试件内部微裂缝的产生和发展十分敏感。J.D.Stauffer等[12]研究表明，利用非线性VAM技术能有效识别混凝土早期损伤的发展。

目前多数成果大多集中在研究传感信号的非线性损伤系数的规律上，而对影响信号非线性成分产生的主要因素及影响规律缺乏深入研究，并且对于混凝土梁早期“受弯微裂缝”的非线性损伤识别研究较少。基于此，笔者以混凝土梁结构下部早期受弯微裂缝为研究对象，利用VAM技术，从理论和试验两个方面展开研究，明确混凝土梁微裂缝开合(呼吸作用)诱发非线性传感信号的原因与影响因素，并建立了微裂缝的几何尺度、调制信号特征参数与传感信号非线性特征之间的定量关系，将建立基于传感信号非线性特征的微裂缝状态识别与监测技术进一步运用于混凝土损伤监测领域奠定基础。

1 非线性振动声调制理论

VAM技术与其他非线性超声检测法相比，最为显著的差别是VAM法需要两个激励信号。其中高频(High Frequency,HF)超声波信号作为损伤的探测信号(Probing Wave)，低频(Low Frequency,LF)振动模态或是振动激励作为泵浦波(Pumping Wave)进一步激发损伤的非线性响应。在理想情况下，当被测对象完全为线性时，响应信号频谱仅显示原激励信号，即高频信号和低频信号。但是当被测对象为非线性时(如微裂缝开合效应等)，响应信号的频谱会显示出除基频以外的其他频率分量，如高次谐波的出现，高频周围的调制旁频现象等(见图1)，利用该效应可以识别混凝土微裂缝的开合问题。

图1 振动声调制技术原理图

为了更具体地描述振动声调制的物理机理，采用理论推导方式进行简要说明。假设为一维波动问题，其非线性一维波动方程(只保留应力-应变关系的二阶非线性项)为[11]

(1)

式中:c为波速；β为非线性系数；u为坐标x处的位移；t为时间。

根据扰动理论[13]，假设一维非线性波动方程的解为

u=u(0)+βu(1).

(2)

式中:u(0)和u(1)分别为系统的线性位移和非线性位移。

当向系统输入两束纵波时，不考虑声波衰减的影响，其线性位移u(0)可表示为

u(0)(x,t)=A01cos(ω1τ)+A02cos(ω2τ).

(3)

τ=t-x/c.

(4)

式中:A01和A02分别为低频和高频激励幅值；ω1和ω2分别为两束纵波的频率。

进一步假设该非线性位移与波传播的距离成正比，即

u(1)=xh(τ).

(5)

式中：h(τ)为未知函数。将式(3)、式(4)和式(5)代入式(2),再代入式(1)，最后得到响应信号位移方程:

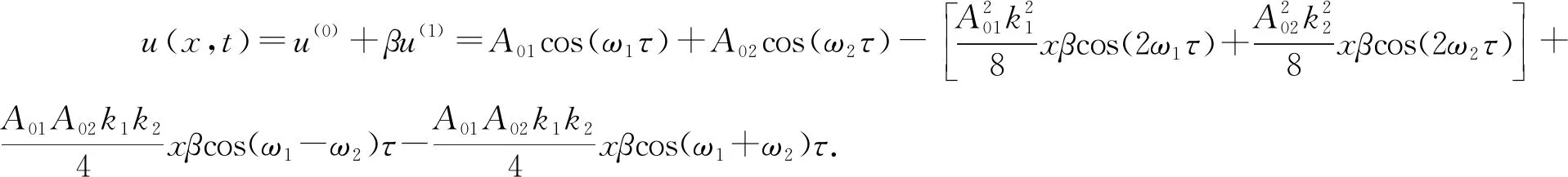
(6)

式中：ki=ωi/c(i=1,2)。

从式(6)可见，响应信号位移方程中不仅有基波存在，而且还产生了高次谐波分量(2ω1和2ω2)以及旁频分量(ω1±ω2)，并且这些分量都与非线性系数β有关。

从式(6)中可以推导出旁频幅值表达式：

(7)

对式(7)进行变换，即可推导出非线性系数β与旁频和基波幅值的关系表达式：

(8)

非线性系数β反映了当波穿过非线性材料时波形发生畸变的程度，可以被用来作为描述介质非线性的量化指标。对于固体材料，其波动非线性主要来源于两个方面：经典非线性和接触非线性。这些非线性源的存在导致超声波与其相互作用时发生强非线性失真，产生高次谐波以及旁频分量[14-16]。笔者研究重点为混凝土梁闭合弯曲裂缝的监测问题，属于接触非线性，因此非线性系数β可以用来表征混凝土梁闭合裂缝发展和开合状态。

在固定激发频率下，一般用β′来取代非线性系数β，作为非线性损伤指标[17]:

(9)

2 非线性振动声调制试验

在通过理论分析探讨了非线性旁频效应影响因素的基础上，笔者通过试验研究各因素及裂缝尺度变化对非线性效应的影响规律，以验证非线性VAM进行混凝土梁微裂缝检测的有效性。

2.1 试件制作及损伤的引入

试件的制作主要分为两个部分，制作混凝土梁和压电智能骨料。混凝土梁采用C30商品混凝土浇筑，长×宽×高为600 mm ×120 mm×100 mm。脱模后，将试件按标准养护环境(23 ℃和95%相对湿度)养护28 d。损伤状态共分为两种：健康状态H和微裂缝损伤状态W。微裂缝损伤采取三点弯曲加载生成，加载前在梁下部中端预留缺口，确保微裂缝处在预设的位置。为了防止试样在弯曲试验中的脆性破坏，将直径为6 mm的带肋钢筋放置在试样底部表面上方15 mm处。在三点弯曲测试期间，利用裂纹检测器(MG10085-1)记录弯曲裂纹的损伤发展。压电智能骨料采用PZT-4压电陶瓷元件及外包水泥制成。PZT-4压电陶瓷元件参数见表1。

表1 PZT-4基本技术参数

2.2 试验装置及激励参数优化

现场试验装置的布置与连接如图2所示。

图2 试验装置

激励参数的优化主要考虑两个方面，即激励幅值和激励频率。首先对低频激励参数进行研究，用VAM技术分别对健康状态和裂缝长度为15 mm的梁进行检测。为保证良好的激励效果，低频频率设置为500～3 000 Hz，每隔100 Hz进行取点激励；高频激励设置为20～50 kHz，每隔1 kHz取点激励。低频激振力(电流控制)设置为5 A，高频激励信号频率设置为20 kHz，幅值为200 V，并保持不变。非线性信号强度的表征采用调制指数MID进行表征[18]

(10)

式中：An±为接收信号中n阶边频的幅度；A0为接收信号中高频信号的幅值。本次实验n取值为2，考虑二阶旁频。

图3分别为高、低频不同激励频率与调制强度的关系曲线。其中图3(a)展示出了低频激励频率对调制强度的影响，从图中可以看出，无论是健康试件还是有损试件，在500～1 000 Hz内，调制强度较高，且调制指数最高在900 Hz处达到了-5 dB附近。低阶模态能量较高，对裂缝开合影响较大，导致调制强度增大。为能更好地观察旁频，且减少模态混叠的影响，选取频率为900 Hz作为后续研究的低频频率参数。

从高频激励频率对调制强度的影响中可以看出(见图3(b))，不同高频频率的激励下调制指数的差距较大，并无明显规律，但从图中可以看出，20 kHz处调制指数达到最大，因此，为更有效地进行损伤识别，可选取该频率作为高频激励频率。

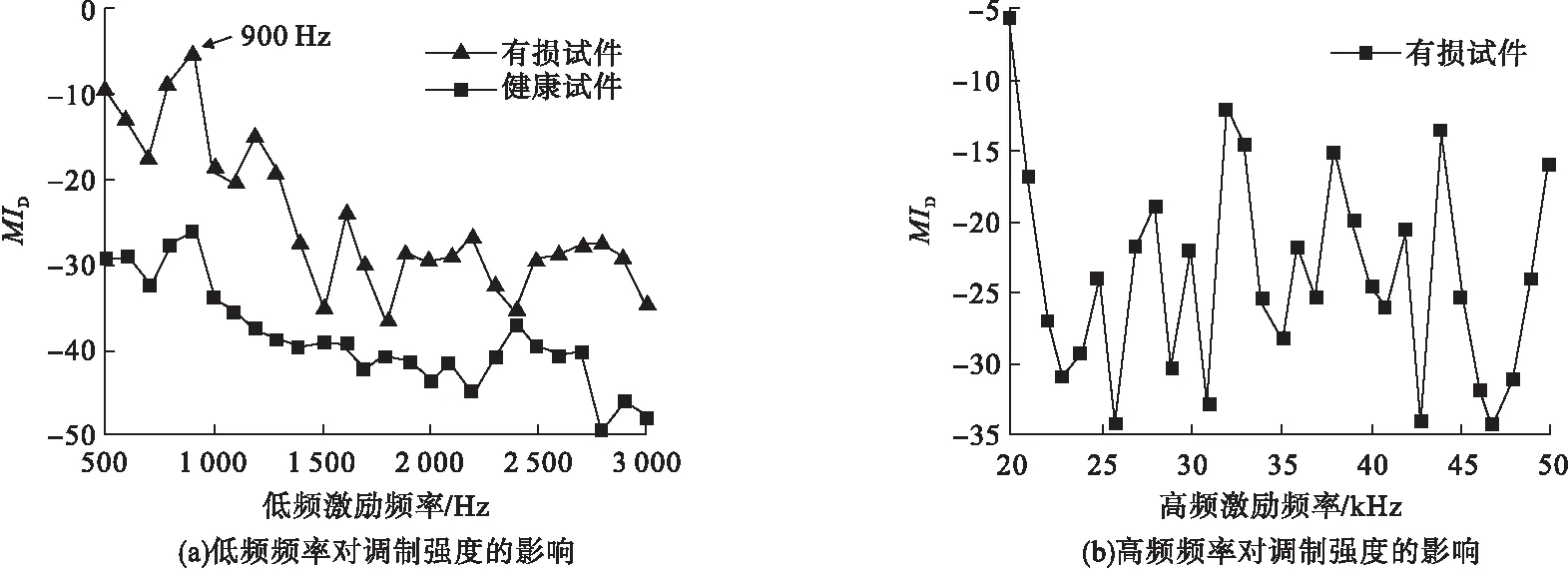
图3 频率对调制强度的影响

将激励器电流从0.5～7 A以0.5 A为步长逐步增加，得到低频幅值对调制指数的变化关系曲线(见图4(a))。从图中可以看出，在前期主要分为两个增长阶段，分别为急速的线性增长阶段和较为平稳的增长阶段；而在后期则变为较平稳的不增长阶段，并且两种工况所达到阈值的大小差别较大。有损试件在激振电流达到5 A时达到阈值远远高于健康试件的2.5 A，这是因为在阈值处，试件内的微裂缝已充分开合对高频信号的调制效应达到最大，阈值越大说明微裂缝损伤越大，符合实际情况。

以高频激励幅值作为研究参数，将高频信号输入电压从100～400 Vpp以10 Vpp为步长逐渐增加，以此分析其与对非线性效应的影响关系，得到旁频幅值与高频幅值的关系曲线(见图4(b))。从图中很明显地看到，左右旁频幅值随高频激励电压呈线性增加趋势。将高频信号和低频信号幅值分别记为A1和A2，左旁频信号幅值记为As(右旁频信号类似)，得到A1A2与As试验拟合曲线如图4(c)所示。从图中可以看出，A1A2与As有着极好的线性关系，且该拟合曲线的斜率即为非线性系数β′，说明高频幅值的变化对非线性系数β′的影响较小，但对旁频幅值的影响较大，更大的高频幅值能够在频域中更容易地观察到旁频分量，因此在损伤检测过程中可尽量提高高频激励幅值。

图4 激励幅值对调制效应的影响

从上述针对激励参数的优化研究中，可基本确定信号的激励参数，即低频激励频率可取900 Hz，幅值可取5 A(换算激振力为71.4 N)；高频激励频率可取20 kHz，其幅值越大，则非线性调制旁频越明显，因此可取信号放大器最大支持峰值电压400 Vpp。

图5和图6分别为激励参数优化后健康状态和有损状态下VAM信号的时域和幅频图。从图5(a)可以看出，除了幅值明显的降低外，其调制波形相较于图6(a)健康状态发生了较为明显的畸变，这些畸变在幅频表现为旁频分量的出现(见图5(b))，并且有损试件的旁频分量呈现的强度要明显高于健康状态。因此，振动声调制技术能够很好地运用于混凝土早期受弯微裂缝的损伤检测。

图5 有损试件接收信号

图6 健康试件接收信号

2.3 损伤识别分析

利用三点弯曲加载分别实现对同一尺寸、材料及养护条件下的两个试件损伤发展。每个试件分别设置7个损伤阶段，试件1分别为裂缝长度为0 mm(健康状态)、4 mm、8 mm、18 mm、28 mm、72 mm、100 mm；试件2分别为裂缝长度为0 mm(健康状态)、5 mm、15 mm、25 mm、50 mm、70 mm、100 mm。图7为试件1中较为典型的4个损伤阶段的裂纹形貌。从图中可以看出，裂纹形态具有一定的不规则性，在试验过程中裂缝长度的取值均为估测值。

图7 试件1裂缝形貌

裂缝长度与非线性系数之间的关系曲线如图8所示。从图中可以看出，试件1和试件2的非线性系数与裂缝长度之间的变化规律基本一致。健康状态下，非线性系数接近0，在微裂缝发展早期(0～20%损伤程度)曲线斜率较高，对损伤发展较为敏感；而在微裂缝增长中期(20%～70%损伤程度)，损伤系数增长较缓；在试件完全破坏后，非线性系数急速回落。这种非线性系数的变化规律是由于实际裂缝形态在裂缝长度方向上的分布差异所导致的。

图8 裂缝长度与非线性系数之间的变化关系

实际裂缝形态的示意图如图9所示。从图中可以看出，裂缝界面由于开合接触作用分为微裂缝区和宏观裂缝区。在损伤早期微裂缝区占主导，裂缝开合对高频信号的调制效应明显，敏感程度较高；但随裂缝长度的进一步增加，宏观裂缝区慢慢占据主导地位，调制效应减弱，直至完全破坏后，微裂缝区几乎忽略不计，所产生的非线性效应与健康状态相近，导致非线性系数的回落。

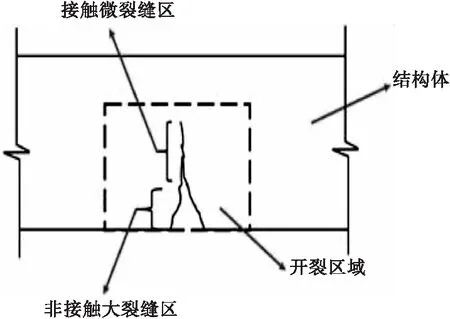
图9 试件实际裂缝示意图

3 结 论

(1)在针对激励频率参数的优化试验中，由于结构低阶模态能量较高，调制强度随低频频率整体出现由高到低的递减规律，而高频频率与调制强度之间并无明显规律。调制强度越大，非线性效应越明显。

(2)在针对激励幅值参数的优化试验中，高频幅值与旁频幅值关系呈线性正相关，高频幅值的增长能有效提高非线性效应；低频幅值与旁频幅值关系呈非线性变化，有明显的阈值现象产生，达到阈值后裂缝截面由于在开合作用下对探测波的调制效应达到最大，因此阈值越大，说明损伤越严重。

(3)损伤识别试验结果表明，VAM能够对损伤程度在0%～70%的混凝土梁有较好的识别敏感度。因此非线性VAM技术能够很好地实现结构早期微裂缝的损伤识别，且能保证较好的敏感性。