特种车辆重载电动轮用轮毂电机热特性分析及冷却水道优化

刘浩，吴学雷，李洪彪，白锦洋，张冉

（北京航天发射技术研究所，北京 100076）

特种车辆重载电动轮集成轮毂电机、制动器、减速器和承载装置，具有结构紧凑、承载载荷大、输出转矩高等特点，但轮毂电机安装空间小、散热条件差，容易导致电机温升过高，从而影响驱动特性以及使用可靠性和安全性，因此，准确分析轮毂电机温度场和合理设计冷却水道具有重要意义。

目前，国内外学者对电机温度场的研究方法主要分为集中参数热路法和数值计算方法。集中参数热路法将各部分损耗集中在相应节点上，将温度场等效为热路或热网络模型求解。MELLOR 等提出了电机等效热路模型，并验证了该模型有效性。BOGLIETTI 等将MELLOR 热阻模型简化为串联热阻模型，提出了简化热网络模型。SHEN Yanhua等基于集中参数热路法对混动越野货车用轮毂电机进行了瞬态温升分析，并通过试验验证了计算方法的准确性。集中参数热路法计算量小，但只能计算各节点的平均温度，计算精度依赖于节点划分。

电机温度场分析的数值计算方法可分为有限元法、有限体积法、有限公式法。基于有限元法的电机温度场计算可以对电机中的热传导问题进行数值计算，但依然需要采用经验公式计算散热面的对流换热系数。基于有限体积法的温度场分析不仅可以求解热传导问题，还可以求解流固耦合面的对流换热问题以及流体流动情况，应用较广泛。KIM等针对25 kW 风冷外转子轮毂电机使用计算流体力学（Computational Fluid Dynamics，CFD）软件进行了电机内流场及温度场分析。ATKINSON等、VLACH 等、RÖNNBERG 等和LIM等均应用CFD 研究了电机温度场分布，并通过试验验证了基于CFD 的电机温度场仿真的正确性。有限公式法又称为元胞法，是由TONTI提出的数值计算方法，具有物理意义明确、控制方程局部积分守恒性好等优点。朱高嘉等分别应用有限公式法和流固耦合法计算永磁电机温度场，二者的计算结果较相似。佟文明等应用有限元法、有限体积法、有限公式法计算了永磁电机温度场，并通过试验验证了应用3 种数值方法分析电机温度场的有效性。用于电机温度场分析的不同数值方法中，这3 种方法的计算精度均可以满足工程应用需求，有限公式法收敛较快、计算量较小，有限体积法在流固耦合计算方面具有优势。

本文以重载电动轮用轮毂电机为研究对象，对轮毂电机温度场和冷却水道优化进行研究。采用考虑旋转磁化和谐波磁场的方法计算轮毂电机额定工况下的定子铁耗，分别采用基于有限体积法的流固耦合分析和基于热网络法的磁热耦合分析计算额定工况电机温度场。通过轮毂电机温升试验验证了两种温度场分析方法的正确性。对不同结构冷却水道的热阻和压降进行了理论分析，针对螺旋型水道采用Pareto 遗传算法进行多目标优化，在水道换热效果基本不变时有效降低了压降。

1 轮毂电机电磁场分析

本文所研究的轮毂电机是集成电动轮中的永磁同步电机，基本技术参数见表1。

表1 永磁同步电机参数

轮毂电机各项损耗是热源。为计算电机电磁损耗，基于Ansys Maxwell 软件进行电机电磁场仿真分析，得到电机定子不同区域磁密波形并将其分解为径向磁密和切向磁密。图1 为定子铁心典型区域的磁密波形，其中为径向磁密，为切向磁密。

图1 定子铁心典型区域的磁密波形

2 轮毂电机损耗计算

轮毂电机损耗可分为机械损耗、永磁体涡流损耗、绕组铜耗和铁心损耗。

机械损耗主要包括电机轴承摩擦损耗和转子风摩损耗，采用式（1）～（2）计算：

式中：为轴承摩擦损耗，W；为常系数，取值范围为1～3；为转子质量，kg；为转速，r/min。

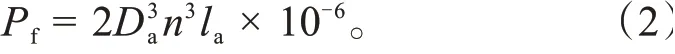
式中：为转子风摩损耗，W；为转子直径，m；为转子长度，m。

永磁体涡流损耗是由交变磁场在永磁体内产生的涡流造成。由于永磁≤体嵌入转子铁心，散热条件较差，涡流损耗对永磁体温升影响较大。采用有限元法计算永磁体涡流损耗，单位体积内永磁体涡流损耗计算表达式为：

式中：为永磁体涡流损耗，W；为涡流密度，A/m；为永磁体电导率，S/m；为体积，m。

绕组铜耗是绕组中相电流产生的欧姆损耗，其计算公式为：

式中：为铜耗，W；为相数；为相电流有效值，A；为工作温度下的相电阻，Ω。

铁心损耗分为磁滞损耗、涡流损耗和附加损耗，通常采用Bertotti 铁耗分离模型计算。由于Bertotti 铁耗模型忽略了旋转磁化和谐波磁场的影响，在计算调速范围较广的轮毂电机铁耗时有较大误差。忽略转子铁耗，基于Bertotti 铁耗模型采用考虑旋转磁化和谐波磁场影响的计算方法计算定子铁耗，计算表达式为：

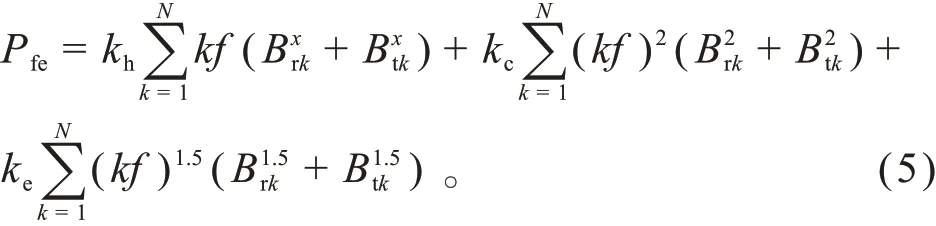
式中：为铁心损耗，W/kg；、为磁滞损耗系数；为电频率，Hz；为涡流损耗系数；为附加损耗系数；为谐波次数；为最高谐波次数；为径向磁密第次谐波幅值，T；为切向磁密第次谐波幅值，T。

由式（5）计算出第区域的铁耗密度P，则电机定子总铁耗为各区域铁耗和，计算表达式为：

式中：为定子总铁耗，W；为铁心长度，m；为硅钢片密度，kg/m；S为铁心第区域面积，m。

采用上述方法计算额定工况下电机各项损耗，结果见表2。

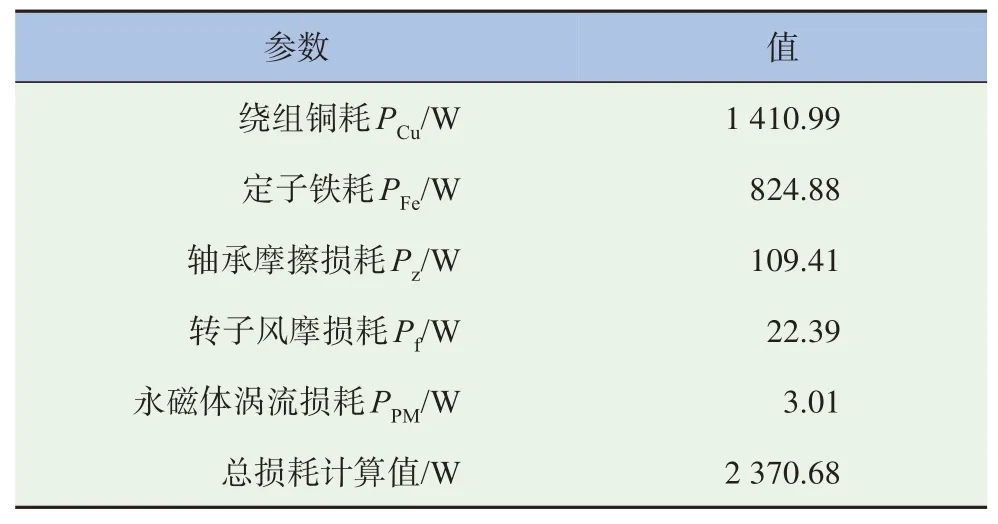
表2 额定工况电机损耗

3 基于有限体积法的流固耦合温度场分析

3.1 控制方程

由传热学原理可知，直角坐标系下，电机内温

度场的控制微分方程和边界条件为：

式中：λ、λ、λ分别为材料、、方向的导热系数，W/（m·K）；为温度，K；q为热源密度，W/m；为密度，kg/m；为热容，J/（kg·K）；为边界温度，K；为时间，s；、、为边界；为冷却介质温度，K；为对流换热系数，W/（m·K）。

由计算流体力学可知，冷却介质为紊流时需满足的控制方程为：

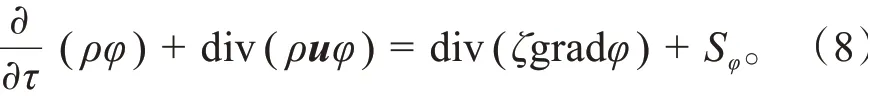
式中：为通用变量；为拓展系数；S为源项；为速度矢量。

3.2 求解域模型的建立

对轮毂电机实际模型进行合理简化，建立1/8周期性模型，其中包含冷却液、机壳、端盖、定转子、绕组、永磁体、转轴和轴承，如图2所示。

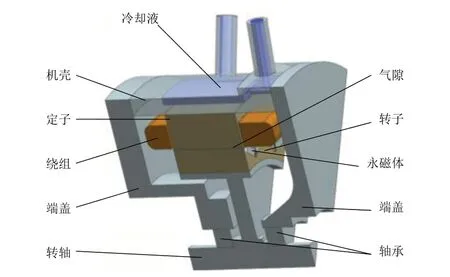
图2 轮毂电机求解域模型

3.3 热源计算

根据表2 中的额定工况电机损耗计算结果和部件体积可以求得各部件的生热率，见表3。将电机各项损耗以生热率的形式施加到相应部位。

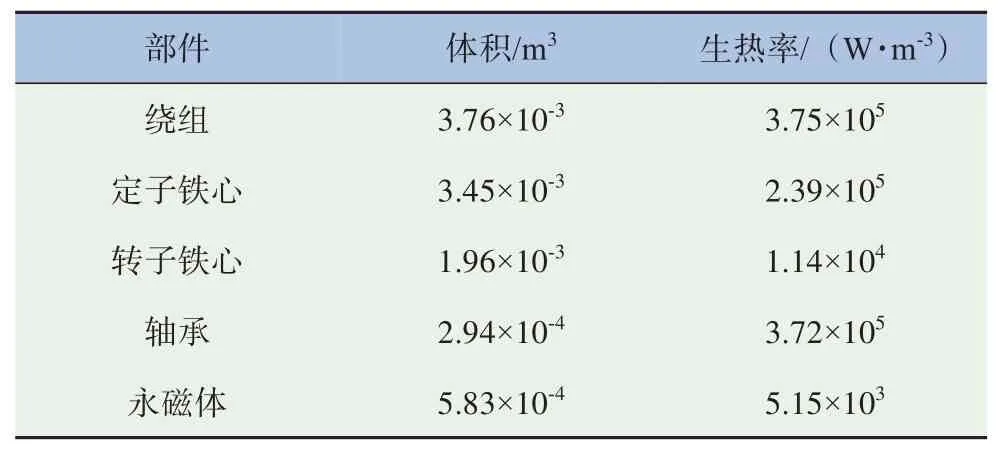
表3 额定工况各部件生热率

3.4 模型等效

3.4.1 绕组和绝缘层的等效

轮毂电机绕组形式为双层散嵌绕组，定子槽内含有槽绝缘、层绝缘、漆包线、浸渍漆。由于槽内漆包线分布不均，且漆包线之间充满浸渍漆，所以难以按照实际绕组模型建模。将实际绕组和绝缘系统模型进行合理简化，将定子槽内的多种绝缘材料等效为一层绝缘层，将漆包线等效为实体绕组，绝缘层与定子槽和等效绕组相接触，如图3所示。

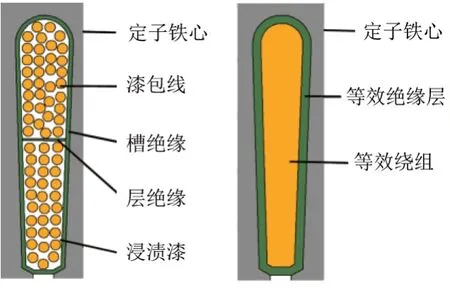
图3 等效绕组和绝缘层

等效绝缘层的导热系数可按式（9）计算：

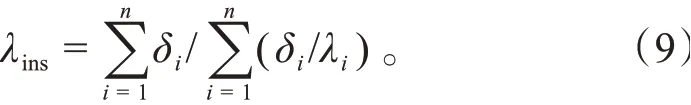
式中：为等效槽绝缘导热系数，W/（m·K）；δ为绝缘材料的等效厚度，m；λ为绝缘材料的导热系数，W/（m·K）。

3.4.2 气隙的等效

轮毂电机转子旋转引起电机内空气流动，加强了定转子与内空气之间的换热。为减小计算量，通常将定转子之间的气隙视为静止的等效空气层，依据气隙内的流动状态计算等效空气层的导热系数。气隙的雷诺数和临界雷诺数分别为：

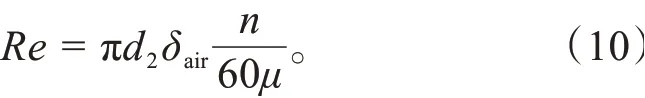
式中：为转子外径，m；为气隙长度，m；为转速，r/min；为空气运动黏度，m/s；为定子内径，m。

气隙雷诺数小于临界雷诺数时，气隙内为层流，等效导热系数与空气导热系数相同；气隙雷诺数大于临界雷诺数时，气隙内为紊流，等效导热系数计算表达式为：

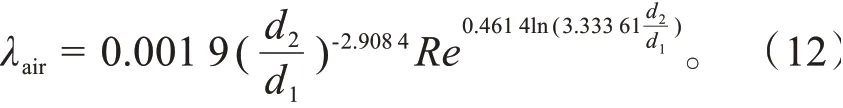
3.5 温度场分析

基于Fluent 建立轮毂电机流固耦合温度场仿真模型。为减小计算量，作以下假设：

（1）冷却液为不可压缩流体。依据冷却液流量及水道结构参数计算出雷诺数为4 714.93，流动模型采用-湍流模型。

（2）忽略电机外表面与空气的对流换热。

（3）材料导热系数恒定，忽略热辐射的影响。

（4）损耗以生热率形式均匀分布在相应部件上，忽略损耗的不均匀分布。

（5） 定子铁心与机壳间的装配间隙等效为0.075 mm厚的空气层，其余部件相互接触良好。

电机在额定工况运行时，边界条件设置如下：

（1）依据轮毂电机温升试验时的环境温度和冷却液入口温度，仿真环境温度为22.5 ℃，冷却液入口温度为27.4 ℃。

（2）冷却介质为50%乙二醇，入口流速为2.075 m/s。冷却液出口为压力出口边界条件。

（3）绕组端部及定转子端面与电机内空气之间的对流换热系数按照文献［18］计算。

（4）冷却液与机壳接触面为流固耦合交界面。电机求解域模型的各个截面均为周期性边界条件。

基于上述边界条件和假设，对轮毂电机额定工况温度场和冷却液流场进行求解，电机稳态温度场仿真结果如图4所示，冷却液流速分布如图5所示。

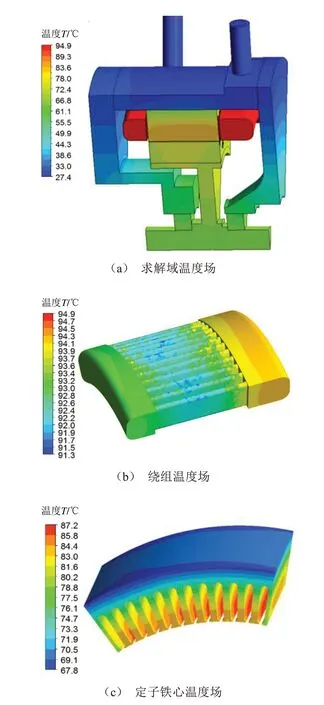
图4 额定工况轮毂电机温度场

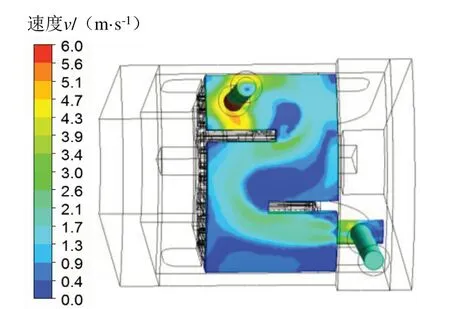
图5 冷却液流速分布

由图4 可知，额定工况下电机绕组温升最高。由于绕组端部与电机内空气间的对流换热作用较弱，绕组产生的热量主要通过绝缘层、定子铁心传导至机壳，再通过机壳与冷却液间的对流换热散出，所以绕组温度分布不均，其中，绕组端部温升最高，与绝缘层接触的绕组中部温升相对端部较低。由图5 可知，水道折返处冷却液流速较低，且存在死水区，使水道换热效果下降，流阻上升。

额定工况下轮毂电机绕组端部、定子铁心、永磁体和轴承的温度变化曲线如图6 所示。在0～1 000 s 内，电机各部件温度接近线性增加，随后增加速度变慢，直至7 000 s 整体温度趋于稳定。电机温度场达到稳定时，绕组端部温度为94.2 ℃，定子温度为77.6 ℃，永磁体温度为75.7 ℃，轴承温度为65.5 ℃。

图6 轮毂电机各部件温度变化

4 基于热网络法的磁热耦合温度场分析

热网络法是将电机中的损耗和热阻用集中热源和等效热阻表示，依据热量传递路径建立网络拓扑关系，运用电路理论求解电机关键节点温度的计算方法。电机中的绕组电阻、永磁体性能受温度影响较大，电机磁热耦合分析以电磁损耗为热源进行温度场求解，并将得出的温度传递至电磁场，引起绕组、永磁体等材料属性的变化，导致电磁损耗发生变化，从而引起温度场的变化。电磁场和温度场间交换损耗和温度数据，反复迭代计算直至达到稳定。图7 为磁热耦合求解过程，其中为温度计算允许误差，本文取为0.1%。

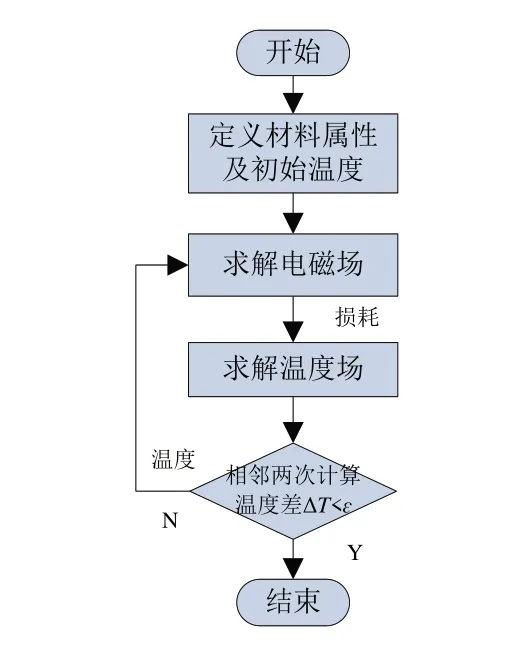
图7 轮毂电机磁热耦合求解过程

基于Motorcad建立轮毂电机热网络和磁热耦合稳态温度场分析模型，图8 为轮毂电机热网络模型及额定工况下各节点稳态温度分布。由图8 可知，额定工况下达到稳态时绕组端部温度为93.7 ℃，定子轭部温度为72.1 ℃，定子齿部温度为81.4 ℃，永磁体温度为72.7 ℃，轴承温度为63.5 ℃，与基于有限体积法的流固耦合分析结果较为一致。

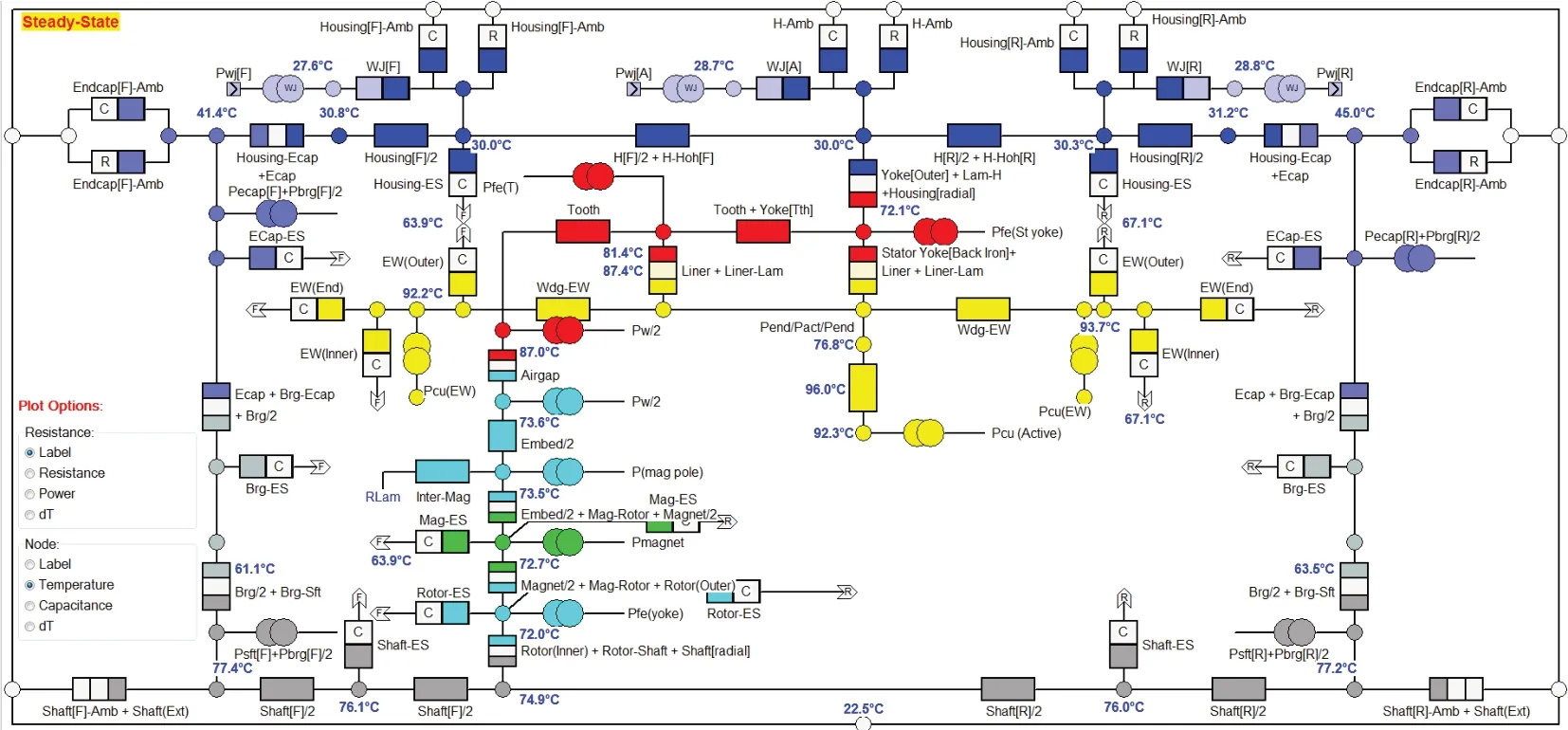
图8 轮毂电机热网络模型和稳态温度分布

5 轮毂电机温升试验验证

为验证轮毂电机温升是否符合要求，在试验台架上对轮毂电机进行额定工况下的温升试验，试验台架如图9所示。

图9 轮毂电机温升试验台架

试验时，轮毂电机按额定功率和额定转矩运行，温度传感器埋置在绕组端部，观察记录绕组端部温度，当温度传感器的温度基本不发生变化时，认为轮毂电机达到热平衡。

分别采用有限体积法和热网络法对额定工况下轮毂电机温度场进行瞬态仿真计算，其中绕组端部温升曲线仿真结果和试验结果如图10 所示。由图可知，额定工况下轮毂电机经过120 min 达到热平衡，此时绕组温度试验值为96 ℃。基于有限体积法的绕组端部温度仿真值为94.2 ℃，仿真值与试验值误差为1.8%；基于热网络法的绕组端部温度仿真值为93.6 ℃，仿真值与试验值误差为2.5%，两种方法的计算误差均在合理范围内。

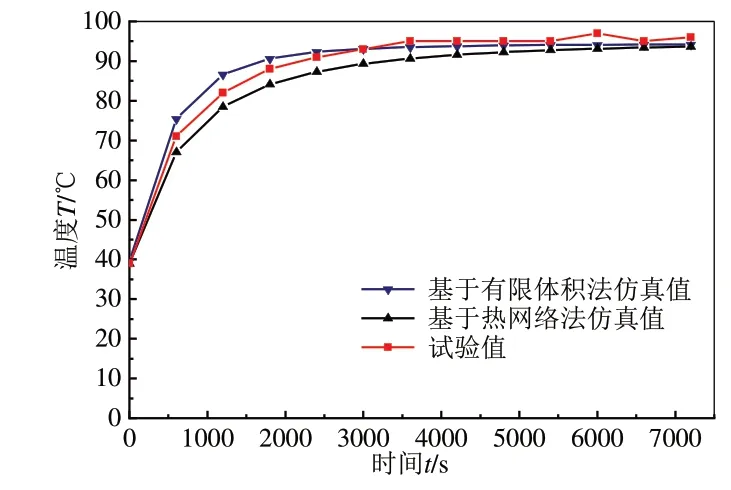
图10 绕组端部温升曲线仿真和试验对比

6 基于Pareto遗传算法的冷却水道优化

6.1 不同结构冷却水道的热阻和压降分析

轮毂电机采用水冷结构，常用的冷却水道结构分为螺旋型和轴向折返型，图11 为两种形式冷却水道的结构示意图。

图11 两种形式冷却水道结构

冷却水道冷却液与机壳对流换热热阻越小，则换热效果越好，对流换热热阻计算表达式为：

式中：为对流换热热阻，℃/W；为水道换热面积，m；为对流换热系数，W/（m·K）；为努赛尔数；为冷却液导热系数，W/（m·K）；为当量直径，m；为雷诺数；为普朗特数；为冷却液流速，m/s；为冷却液运动黏度，m/s。

冷却水道压降由沿程阻力压降和局部阻力压降组成，计算表达式为：

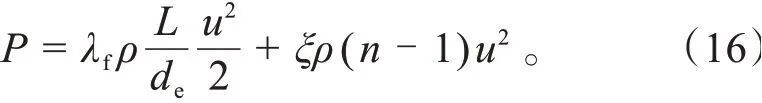
式中：为压降，Pa；为沿程阻力系数，=0.3 164/（2 300<10）；为冷却液密度，kg/m；为水道总长度，m；为局部阻力系数；为折返水道数目。

用式（13）和式（16）计算螺旋型和轴向折返型水道的对流换热热阻和压降，研究冷却液流量对两种水道的对流换热热阻和压降的影响，如图12 所示。在换热效果基本相同时，螺旋型水道压降较轴向折返型水道小，经济性更好。此外，水道的结构尺寸参数对换热效果和压降的影响较大，在确定水道结构尺寸参数和流量时需要综合考虑换热效果和压降两方面的影响。为确定螺旋型水道最优的结构尺寸参数和冷却液流量，将对螺旋水道进行多目标优化。

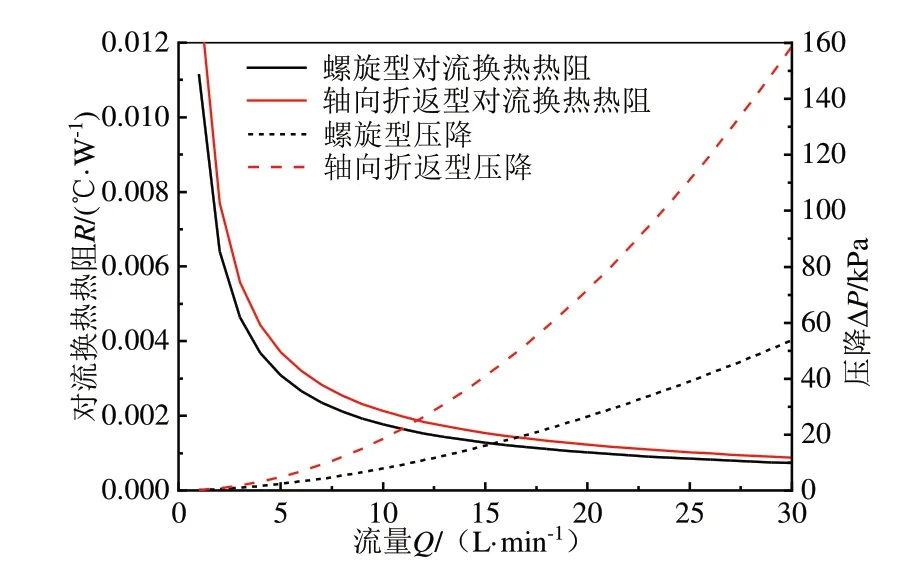
图12 流量对不同水道热阻和压降的影响

6.2 Pareto最优解

对于多目标优化问题：

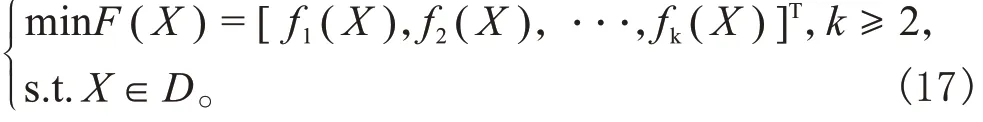
式中：为优化变量；（）为目标函数；（）（≥2）为子目标函数；为优化变量可行域。

Pareto 最优解的定义为：在可行域内，对于变量X ，当且仅当不存在其他变量使其在约束条件下满足：（1）（）≤（X ）；（2）至少存在一个使（）＜（X ），则X 为Pareto最优解。所有Pareto 最优解构成Pareto 最优解集，其对应的目标函数构成了Pareto前沿。

6.3 螺旋型水道优化及结果分析

冷却水道的换热效果和压降一般是相互矛盾的，不存在使换热效果和压降同时达到最优的最优解，只存在Pareto 最优解。如果采用将热阻和压降进行线性加权的方式将多目标优化转化为单目标优化，则优化结果对权重的依赖性较大。基于Pareto遗传算法对螺旋型冷却水道进行多目标优化，选取螺旋水道宽度、水道高度、冷却液流量为优化变量，以对流换热热阻和压降为目标函数，则螺旋水道的多目标优化问题表达式为：

式中：（）为目标函数；（）为对流换热热阻；（）为压降；=［，，］；、分别为优化变量的下限和上限。

使用改进的NSGA-Ⅱ遗传算法对上述问题进行多目标优化求解，遗传算法的控制参数是：编码方式为实数编码，种群大小为200，最大进化代数为300，最优前段个体系数为0.35。经过迭代计算后得到Pareto前沿，如图13所示。为兼顾换热效果和压降的影响，选择Pareto 前沿靠近中间的一组解作为优化方案，优化后水道宽度为16 mm，水道高度为11.4 mm，流量为29.79 L/min。

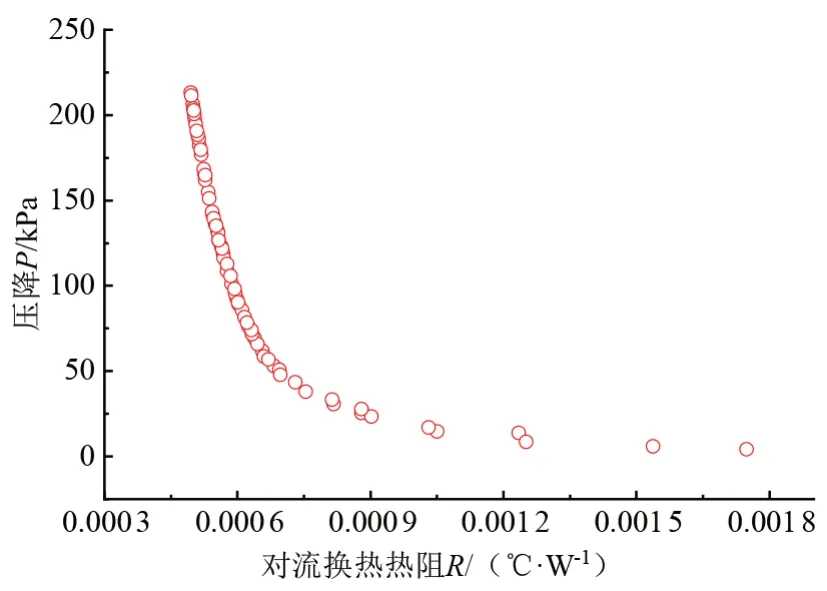
图13 Pareto前沿

采用优化后的螺旋型水道再次进行额定工况下温度场仿真计算，初始方案与优化方案的温度场和压降仿真结果对比见表4。优化后，绕组端部温度基本不变，定子齿部温度降低0.37%，永磁体温度上升0.96%，压降下降22.9%。螺旋型水道优化后在保证散热能力基本不变的情况下，使水道压降降低了22.9%，证明了优化方案的可行性，表明了将Pareto 遗传算法应用到螺旋型水道优化设计中的有效性。

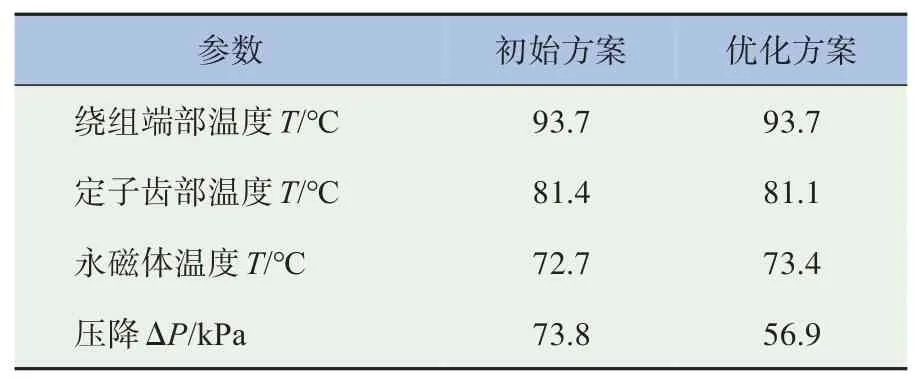
表4 初始方案和优化方案仿真结果对比

7 结论

本文对轮毂电机电磁场进行了有限元分析，分别采用有限体积法和热网络法对轮毂电机温度场进行仿真计算，并通过轮毂电机温升试验验证了两种计算方法的正确性。对不同结构形式冷却水道的对流换热热阻和压降进行了理论分析，基于Pareto 遗传算法对螺旋型冷却水道进行了多目标优化。综上所述，得出以下结论：

（1）基于有限体积法的流固耦合温度场分析可获得轮毂电机各部件的温度场分布及冷却液流场分布情况，计算精度高于热网络法，但计算量较大，且较难实现磁热双向耦合。基于热网络法的磁热耦合温度场分析可以在温度场和电磁场间快速迭代计算，计算量较小，但计算精度受热阻等参数影响较大。当仅计算温度场而不考虑多物理场的耦合计算时，有限体积法计算精度较高。然而单温度场计算精度难以满足应用需求，电机电磁场、流场、温度场的多物理场耦合分析是重要的研究方向，基于有限体积法和热网络法的两种温度场计算方法在与流场或电磁场耦合计算方面各有优劣。

（2）在换热效果相同时，螺旋型水道压降较轴向折返型小，经济性更好。基于Pareto 遗传算法对螺旋型水道进行多目标优化后，在使散热效果基本不变的情况下压降降低22.9%，优化方案具有较高的参考价值。采用Pareto 遗传算法可以得到冷却水道设计变量的最优解集，避免了各优化目标间的权重分配问题，可为设计者提供多种优化方案。